一题多解 开拓视野——对一道电磁感应综合题的思考

王维卫

(浙江省金华第一中学 321015)

求解电磁感应的情景问题，同学们有很多模型套路可走.特别是涉及电容问题，常考常新，非常精彩，在物理高考中备受瞩目.聚焦了高中物理的力与能量两条主线的核心内容，如高中物理的两大定理——动量定理、动能定理.有时还会因为命题者考虑不足，出现在能量方面不能自洽的情况，学习体验自然不好.下面这个题是两个基本模型的叠加，重点强调电路分析的意识，以常规的求电量与功的形式抛砖引玉，分析教学中存在的问题，请大家鉴赏评析.

题目如图1所示,一对光滑的平行金属导轨固定在同一水平面内,导轨间距L=1m,两导轨中间通过一间距可不计的绝缘隔层分开,左端接有电阻和电容器,阻值R1=1Ω,电容C=0.1F,右端接有阻值R2=0.25Ω的电阻.一质量m=0.1kg,阻值不计的金属棒MN放置在导轨上,整个装置置于竖直向上的匀强磁场中,磁场的磁感应强度B=1T.棒在水平向右的外力F作用下,由静止开始以2m/s2的加速度向右运动.当棒运动0.09m时到达绝缘层，同时撤去外力.假设导轨足够长且电阻不计,棒在运动过程中始终与导轨垂直且两端与导轨保持良好接触.求:

图1

(1)棒在匀加速运动过程中,外力F随时间t变化的表达式；

(2)棒在匀加速运动过程中,通过导体棒电荷量q；

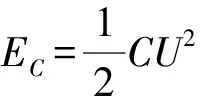
解析(1)棒由静止开始匀加速至绝缘层

由v=at得v=0.6m/s

画出图2的等效电路，

导体棒为电源，

E=BLvI=IC+IR

①

导体棒电阻不计，电容器充电电流

②

流过电阻R1的电流

③

联立①②③得

I=2t+0.2(A)(0≤t≤0.3s)

④

对棒由牛顿第二定律得

F-FA=ma

⑤

又FA=BLI

⑥

联立④⑤⑥得

F=2t+0.4(N)(0≤t≤0.3s)

⑦

图2

(2)解法一利用平均值直接求解

由④式知导体棒中的电流I随时间t是线性变化，可得平均电流

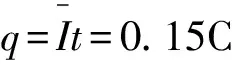
解法二利用并联电路求解

分析电路，由电量守恒定律知

q=qC+qR

⑧

qR也可以将数据代入③式得IR=2t(A)，取电流平均值求.

最终可解得q=qC+qR=0.15C

解法三利用动量定理求解

对导体棒用动量定理得

⑨

代入⑨式得，q=0.15C

(3)求外力做的功W，我们又可从力与能量的角度求得多种解法

解法一利用动能定理进行求解

在棒加速阶段，有

⑩

撤去F后，电容器中的电能转化为R1的焦耳热，导体棒的动能转化为R2的焦耳热.

综合可得WF=0.072J

解法二利用能的转化与守恒定律求解

从能量转化来看，导体棒克服安培力做的功等于电路中的电能.一部分通过R1转化为焦耳热，一部分通过电容器储存起来.由①式得BLI=BLIC+BLIR，将导体棒的安培力分解为两个力，他们做的功可以代数和相加.

克服BLIC做功转化成电容器中的电能，

EC=BLICx=0.018J

克服BLIR做功在电阻R1中产生焦耳热，

代入⑩式即得

WF=0.072J

解法三利用功的本源定义求解

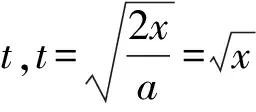
功是力F在位移上的累积，结合⑦式得

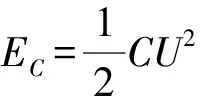
典型错误剖析学生典型的错误就在于不想修路而直接搭桥，不知不觉把导体棒中的电流等同于电阻R1的电流.比如牛顿第二定律由⑤式变成了

求电量由⑧式变成了

动量定理由⑨式成了

看似学生抛弃了⑤⑧⑨这样一些原始方程，实际上根源并不在于此.

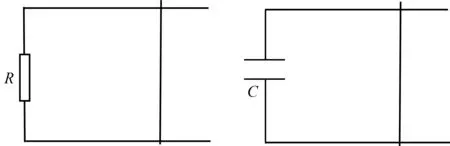
图3 图4

由于导体棒电阻为零，从能量转化的角度去看看第(3)小题的解法.

策略点睛综上所述，我对日常的习题教学有一些想法与各位分享.教师在教学中，用放大镜选题，让例题更具有代表性；用显微镜看题，透视模型后面的物理本质；用照妖镜审题，迅速看出题目架构与陷阱.防止学生解题出现固定思维，需要教师自己提供一些原创题，加强几个基础分析能力的考查，同时拓展学生视野，帮助学生跳出题海，让学习体验更好.习题讲评时，教师要展示解题最基本的操作环节，比如画轨迹图，受力图，等效电路图等等，让思维的痕迹明显一点，更有利于在学生的头脑中发酵.