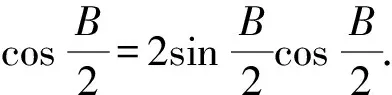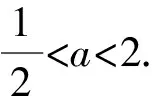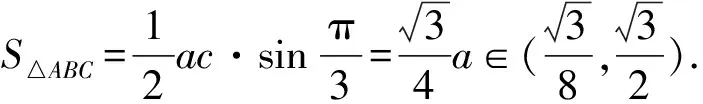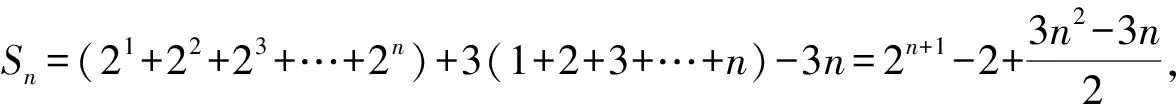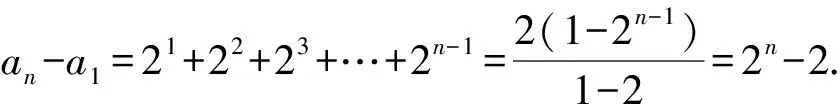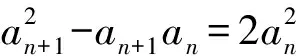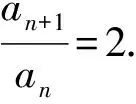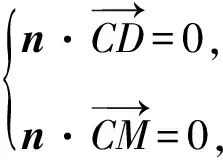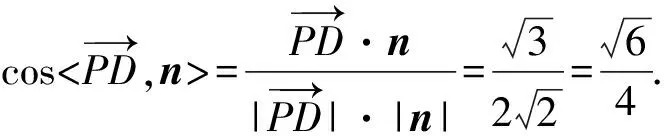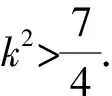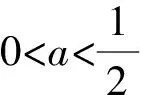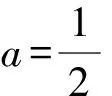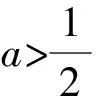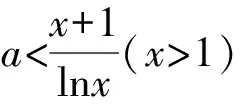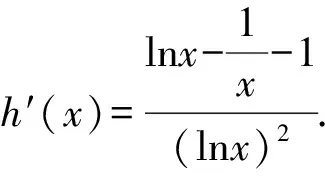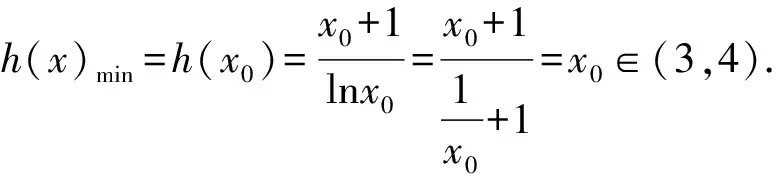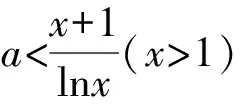2022届高考模拟考试数学试题(本试卷适合新高考地区考生使用)

李昌成

(新疆乌鲁木齐市第八中学 830027)

本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.时量120分钟，满分150分．

第Ⅰ卷

一、单选题(本大题共8小题，每小题5分.在每小题给出的四个选项中，只有一项是符合题目要求的)

1.设φ∈R，则“f(x)=cos(x+φ)(x∈R)为偶函数”是“φ=π”的( ).

A. 充分不必要条件

B. 必要不充分条件

C. 充分必要条件

D. 既不充分也不必要条件

A.第一象限 B. 第二象限

C.第三象限 D. 第四象限

3.已知|a|=2|b|≠0，且关于x的方程x2+|a|x+a·b=0有实根，则a与b的夹角的取值范围是( ).

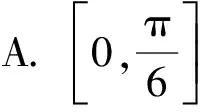
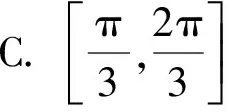
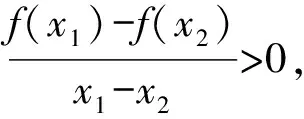
A. 恒大于0 B. 恒小于0

C. 等于0 D. 无法判断

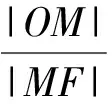
7.如图1，在等边△ABC中，D,E分别是线段AB,AC上异于端点的动点，且BD=CE，现将△ADE沿直线DE折起，使平面ADE⊥平面BCED，当点D从点B滑动到点A的过程中，则下列选项中错误的是( ).

A. ∠ADB的大小不会发生变化

B. 二面角A-BD-C的平面角的大小不会发生变化

C.BD与平面ABC所成的角变大

D.AB与DE所成的角先变小后变大

图1

8.设(lnx)2-lnx-2=0的两根是α，β，则logαβ+logβα=( ).

二、多选题(本大题共4小题，每小题5分.在每个小题给出的选项中，有多项符合题目要求，全部选出的得5分，部分选出的得2分，有选错的得0分)

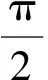
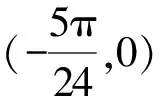
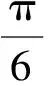
10.在发生公共卫生事件期间，有专业机构认为该事件在一段时间内没有发生大规模群体感染的标志为“连续10天，每天新增疑似病例不超过7人”.过去10日，甲、乙、丙、丁四地新增疑似病例数据信息如下：

甲地：中位数为2，极差为5；

乙地：总体平均数为2，众数为2；

丙地：总体平均数为1，总体方差大于0；

丁地：总体平均数为2，总体方差为3．

则甲、乙、丙、丁四地中，一定没有发生大规模群体感染的有( ).

A. 甲地 B. 乙地 C. 丙地 D. 丁地

图2

B. 若b2=ac，则该双曲线是黄金双曲线

C. 若∠F1B1A2=90°，则该双曲线是黄金双曲线

D. 若∠MON=90°，则该双曲线是黄金双曲线

12.在三棱锥A-BCD中，AB=CD=6，AC=BD=5，AD=BC=7，M，N，P，Q分别为棱AB，CD，AD，BC的中点，则( ).

A. 直线MN是线段AB和CD的垂直平分线

B. 四边形MQNP为正方形

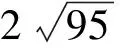
D. 经过三棱锥A-BCD各个顶点的球的表面积为55π

第Ⅱ卷

三、填空题(本题共4小题，每小题5分)

13.直线y=x与曲线y=2ln(x+m)相切，则m=____．

14.已知(1-2x)7=a0+a1x+a2x2+…+a7x7，则|a1|+|a2|+…+|a7|=____.

15.在我国古代数学著作《孙子算经》中，卷下第二十六题是：今有物，不知其数，三三数之剩二，五五数之剩三，七七数之剩二，问物几何？满足题意的答案可以用数列表示，该数列的通项公式可以表示为an=____.

四、解答题(共70分．解答应写出文字说明、证明过程或演算步骤．)

(1)求B；

(2)若△ABC为锐角三角形，且c=1，求△ABC面积的取值范围．

已知{bn-an}为等差数列，{bn}的前n项和为Sn，且a1=2，b1=2，b3=14，____，是否存在正整数k，使得Sk>2021？若存在，求k的最小值；若不存在，说明理由．

19.(本小题满分12分)如图3，在棱锥P-ABCD中，侧面PDC是边长为2的正三角形，底面ABCD是菱形，平面PCD⊥平面ABCD，M是PB的中点，且∠BCD=120°．

(1)求证：PA⊥CD；

(2)求直线PD与平面CDM所成角的正弦值．

图3

(1)求椭圆C的方程；

21.(本小题满分12分)在一个系统中，每一个设备能正常工作的概率称为设备的可靠度，而系统能正常工作的概率称为系统的可靠度，为了增加系统的可靠度，人们经常使用“备用冗余设备”(即正在使用的设备出故障时才启动的设备).已知某计算机网络服务器系统采用的是“一用两备”(即一台正常设备，两台备用设备)的配置，这三台设备中，只要有一台能正常工作，计算机网络就不会断掉．设三台设备的可靠度均为r(0

(1)要使系统的可靠度不低于0.992，求r的最小值；

(2)当r=0.9时，求能正常工作的设备数X的分布列；

(3)已知某高科技产业园当前的计算机网络中每台设备的可靠度是0.7，根据以往经验可知，计算机网络断掉可能给该产业园带来约50万的经济损失．为减少对该产业园带来的经济损失，有以下两种方案：

方案1：更换部分设备的硬件，使得每台设备的可靠度维持在0.9，更新设备硬件总费用为8万元；

方案2：对系统的设备进行维护，使得设备可靠度维持在0.8，设备维护总费用为5万元．

请从期望损失最小的角度判断决策部门该如何决策?

(1)求函数f(x)的单调区间；

(2)令F(x)=af(x)-x2，若F(x)<1-2ax在x∈(1,+∞)恒成立，求整数a的最大值．

参考答案

一、选择题

1.B 2.B 3.B 4.A 5.C 6.D 7.C

8.D 9.AC 10.AD 11.BCD 12.ACD

二、填空题

三、解答题

因为sinA>0，

(2)若△ABC为锐角三角形，且c=1，

由余弦定理，得

由△ABC为锐角三角形，可得a2+a2-a+1>1且1+a2-a+1>a2，

18.选①：由log2an+1=log2an+1，得

log2an+1-log2an=1.

所以{log2an}是首项为log2a1=1，公差为1的等差数列.

所以log2an=1+(n-1)×1=n，故an=2n．

又b1=2，b3=14，a1=2，a3=8，

所以b1-a1=0，b3-a3=6.

所以等差数列{bn-an}的公差

所以bn-an=b1-a1+(n-1)d=3(n-1).

所以bn=2n+3(n-1)，

由Sn>2021得n≥10，即存在正整数k，使得Sk>2021，且k的最小值为10．

选②：由an+1=an+2n,得a2-a1=21，a3-a2=22，a4-a3=23，…,an-an-1=2n-1(n≥2).

又a1=2，所以an=2n(n≥2).

显然a1=2也满足an=2n(n≥2)，故an=2n.

以下解法同选①．

(an+1-2an)(an+1+an)=0.

所以{an}是首项为2，公比为2的等比数列，所以an=2n.

以下解法同选①．

19.(1)因底面ABCD是菱形，且∠BCD=120°，

所以∠CDA=60°.

连接AC，所以△CDA为等边三角形．

取CD的中点O，连接AO，PO，则AO⊥CD，PO⊥CD，又AO∩PO=O，AO，PO⊂平面AOP，

所以CD⊥平面AOP.

又PA⊂平面AOP，所以CD⊥PA．

(2)因为平面PCD⊥平面ABCD，平面PCD∩平面ABCD=CD，OP⊂平面PCD，OP⊥CD，

所以OP⊥平面ABCD.

又OA⊂平面ABCD，所以OP⊥OA，

又OA⊥CD，PO⊥CD，

所以OA，OP，CD两两垂直.

图4

设n=(x,y,z)为平面CDM的法向量，则

令y=1，则z=-1，故n=(0,1,-1).

由以上两式解得a2=4，b2=2.

(2)存在这样的直线．

设所求直线与椭圆相交两点A(x1,y1)，B(x2,y2)，

(1+2k2)x2+12kx+14=0.

①

②

△=(12k)2-4×14×(1+2k2)>0，

可得x2=2x1.

③

21.(1)要使系统的可靠度不低于0.992,则P(X≥1)=1-P(X<1)=1-P(X=0)=1-(1-r)3≥0.992,解得r≥0.8,故r的最小值为0.8.

(2)设X为能正常工作的设备数,由题意可知,X～B(3,r).

所以X的分布列为

X0123P0.0010.0270.2430.729

(3)设方案1，方案2的总损失分别为X1,X2.

采用方案1，更换部分设备的硬件, 使得设备可靠度达到0.9,由(2) 可知计算机网络断掉的概率为0.001,不断掉的概率为0.999,因此E(X1) =80000+0.001×500000=80500(元).

采用方案2, 对系统的设备进行维护, 使得设备可靠度达到0.8,由(1) 可知计算机网络断掉的概率为0.008,因此E(X2)=50000+0.008×500000=54000(元).

因此, 从期望损失最小的角度, 决策部门应选择方案2.

①当a≤0时，由f′(x)>0，

所以∃x0∈(3,4)，使得

从而h(x)在(1,x0)单调递减，在[x0,+∞)单调递增.

所以a

故整数a的最大值为3．