基于动态字典学习的欠定盲语音重构算法
2022-05-23王晓楠杨璟安
魏 爽,王晓楠,杨璟安
(上海师范大学 信息与机电工程学院,上海 201418)
0 引 言
语音盲分离技术性能的提高有利于嘈杂环境中语音的精准获取[1]及计算听觉场景的有效分析[2]。而现实应用中,通常混合后的接收语音数目少于源语音数目,无法使用普通盲源分离方法求解,因此欠定盲源分离(underdetermined blind source separation,UBSS)成为当前语音处理领域需要关注的热难点问题。
稀疏分量分析两步法[3]是实现UBSS的重要技术,根据两步法框架,研究者们引入了压缩感知(compressed sensing,CS)[4]理论以实现源信号恢复。考虑到UBSS优化模型与CS稀疏重构模型的高度一致性[4],需将信号变换至稀疏域进行稀疏表示,其中字典学习算法因适应性强且能精确抓取并存储语音特征[5]成为当前信号稀疏表示的热门方法,如K-SVD算法[6]、MOD算法[7]、正则化同步码字优化(simultaneous codeword optimization,SimCO)算法[8]。文献[9]表明,正则化SimCO算法的字典更新速度及自适应学习性能均优于K-SVD与MOD算法。但对于复杂多变的语音信号,若始终固定信号的分段长度,则字典稀疏效果存在局限性。
本文提出动态字典学习实现欠定盲语音改进算法,通过逐段恢复SimCO字典域的稀疏信号,根据源信号重构结果动态选取合适的分段长度,对稀疏重构过程进行优化迭代从而得到全局最优的重构语音。与传统SimCO算法采用固定的分段长度重构源信号相比,所提算法能够充分利用动态字典学习稀疏结果,进一步精确抓取语音重构特征,提高语音恢复精度。
1 基于CS的分段语音欠定盲分离模型
本文利用源信号在变换域的可稀疏性,构建基于CS的分段语音欠定盲分离模型。即根据UBSS的两步法思路,在第一步估计得出混合矩阵后,构建信号的稀疏表示模型,并对观测信号作分段处理,运用CS稀疏重构算法逐段恢复源信号。
1.1 语音欠定盲分离的基本模型
本文研究的对象是欠定盲信号分离问题的瞬时模型。假设存在n维未知且统计独立的源信号S=[s1(t),s2(t),…,sn(t)]T, 在混合系统中经未知矩阵A混合并引入m维加性观测噪声E=[e1(t),e2(t),…,em(t)]T, 通过m个传感器采集可得到观测信号X=[x1(t),x2(t),…,xm(t)]T, 如图1所示。
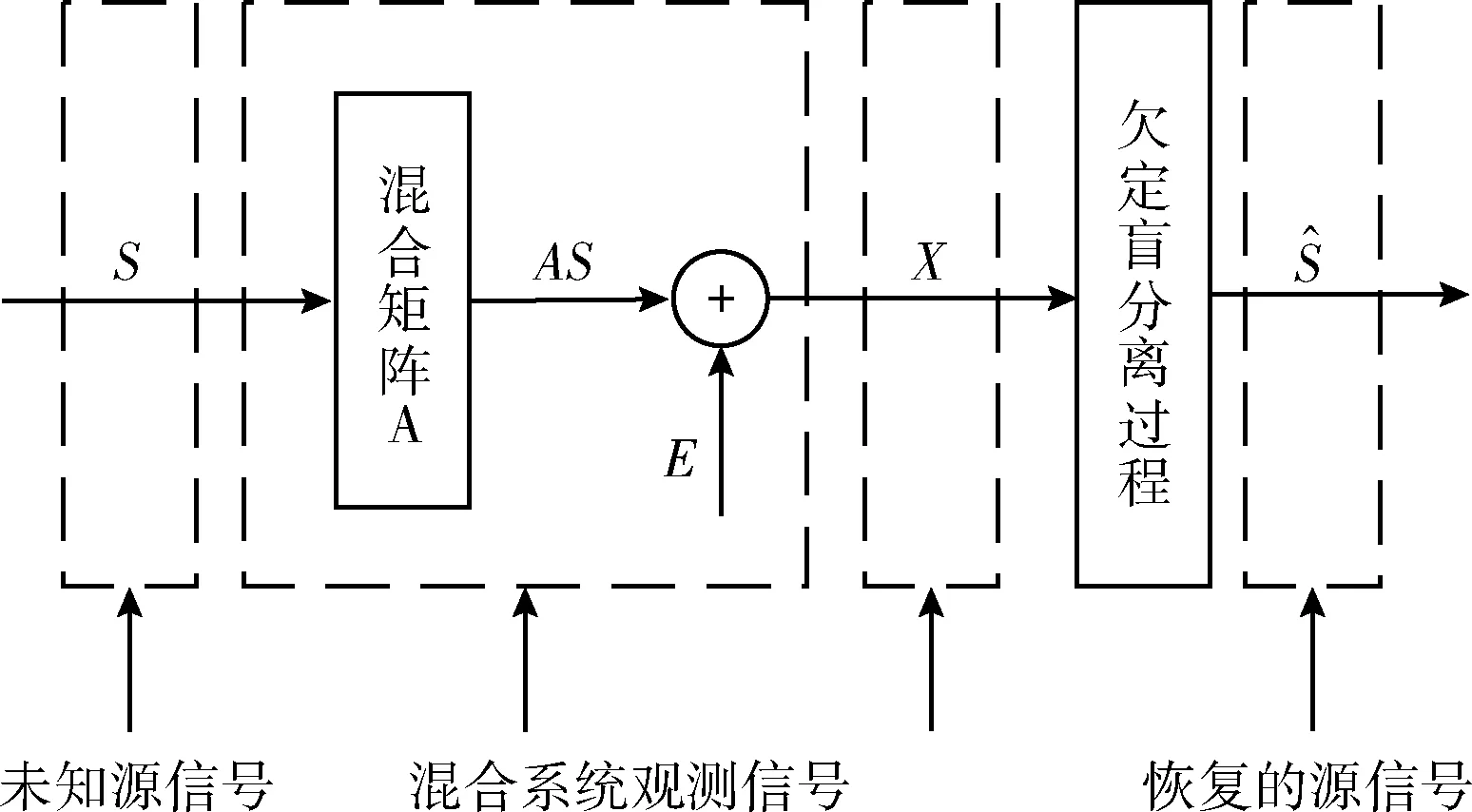
图1 语音欠定盲分离模型
其中,上标 [·]T表示转置运算,t=1,2,…,T,T为采样点数,混合矩阵A=[a1,a2,…,an],ai(i=1,2,…,n) 为A的m维列向量。
为方便描述,忽略系统引入的噪声干扰,即令E=0,则一般的欠定盲源分离数学模型为
X=AS
(1)
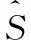
1.2 CS分段语音重构的基本模型
应用压缩感知理论重构语音的核心思想是利用信号在某一变换域中的稀疏性,根据M维观测信号重建N维源信号。由于语音信号的时间长度较长,重建完整信号将大大降低算法效率,因此为将CS基本模型应用于UBSS场景,需对信号做分段处理,如图2所示。

图2 分段语音CS重构模型
将m路T点的观测信号X分段为若干τ点子信号,通过CS重构算法可逐段求得n路T点的源信号S。通过逐段重建子信号,可在降低算法复杂度的同时获得更优的重建效果。
因此,选取某一分段信号为例,对其CS重构模型做以下描述
(2)
其中,τ 分段源信号s可由稀疏基Ψ∈RN×K的线性组合进行表示 s=Ψy (3) 其中,矩阵y∈RK×1为源信号的Ψ域表示,且当y仅有p(p≪K) 项非零系数时称y为p稀疏的,因此式(3)为源信号在变换域的稀疏表示。若混合矩阵Λ与稀疏基矩阵Ψ不相关,将式(3)代入式(2)可构造CS的稀疏重构模型如下 x=ΛΨy (4) 在已知矩阵x与Λ的前提下,需根据稀疏表示方法求解稀疏基Ψ;进而若y的稀疏度满足p (5) 基于正则化SimCO字典学习方法,本文提出动态改变信号分段长度以实现语音稀疏重构的改进算法,即先通过正则化SimCO算法训练冗余字典D,并根据混合信号训练字典(mixture-trained dictionary,MTD)[8]方法在动态选取的不同信号分段长度τ下构造稀疏字典域Ψ,使用稀疏重构算法则可在多次迭代过程中获取重构效果最佳的一组源信号。 正则化SimCO字典学习的目的是寻求最优的冗余字典稀疏表示给定的语音训练数据,该方法能够同时更新字典的任意原子及对应稀疏系数[9],不仅改善了字典学习规模小、更新速度慢的弊端,同时正则化处理很好地解决了原始字典的病态(ill-conditioned)问题。 (6) (7) (8) (9) (10) (11) 为解决CS重构长语音过程中运算复杂度高的问题,同时为提高字典稀疏域下信号的重构质量,可根据最速下降原理[12]中的优化思想动态改变信号分段长度,对分段的语音信号进行稀疏表示,并对比不同分段长度下信号的重构质量,从而在多次优化迭代过程中选取恢复效果最佳的各路源信号。 在CS稀疏信号重构模型中,已知字典域Ψ可根据重构算法求解信号的Ψ域表示,进而恢复源信号。因此在利用正则化SimCO方法求得字典矩阵D的前提下,对于不同的分段长度τ,需采用MTD方法根据D构造不同的字典域Ψ,即:对D∈RL×L以重叠长度F进行矩阵行数的叠加,得到τ行的矩阵Dτ;将Dτ作为对角元素进行n×n的对角矩阵组合,得Ψ∈RN×K。 为量化对比每次迭代过程中稀疏重构的源信号效果,通过计算输出语音信噪比的方式来表征每路源信号的重构准确度σ,定义如下 (12) 在动态字典学习算法的设计过程中,为了动态改变信号的分段长度,将第i路信号在第k次迭代的σ值记作σi(k), 并令前k-1次迭代过程的最优值记为σi_best,通过计算σi_best与σi(k)间的差值Δσi(k)构造差分优化函数,当Δσi(k)<0时表明σi(k)更优,需将σi(k)赋值给σi_best以更新最优值;当Δσi(k)≥0时表明σi_best更优,则σi_best值保持不变。根据差分优化函数的绝对值增大迭代的步长,使σi_best值不断更新,当所求的Δσi(k)小于某一给定的阈值时,则迭代过程最终收敛。 令n路信号在第k次迭代的差分优化函数矩阵如下 Γ(σ)(k)=[Δσ1(k),Δσ2(k),…,Δσn(k)] (13) 其中,k=1,2,3,…, 且Δσi(k)=σi_best-σi(k),i=1,2,…,n。 为了统计分析各路源信号的重构结果,对n路恢复信号的差分函数结果进行均方根计算[13],则n路信号总体重构准确度的变化ΔΓ描述如下 (14) 令相邻两次迭代过程的τ变化值为步长λ,则第k次迭代的信号分段长度为τ(k)=τ(k-1)+λ(k-1)。 根据n路信号的总体重构准确度,增加全局搜索的步长,则依据最速下降思想定义步长 (15) 其中,ι>0为调节步长增量的常系数。 为求得每路信号的全局最优解,需设置阈值ε。由于各路信号通常具备不同的语音特征,其σ值的范围有所差异,因此在[-1,1]范围内,对信号的重构准确度差值Δσi进行归一化处理求得Δσni, 以取得统一的阈值[13]。当满足条件0<Δσni<ε时,则视作第i路信号的优化过程近似收敛,此时该路信号的全局最优值σi_best停止更新;若n路信号的重构准确度差值均满足上述条件,则信号全部收敛,此时算法停止迭代。 因此利用分段稀疏信号的动态重构算法,寻找重构效果最佳的一组源信号的步骤可总结如下: 初始化:初始分段长度τ,初始步长λ,常系数ι,阈值ε。迭代次数k=1。 输入:观测矩阵x,混合矩阵Λ。 输出:各路源信号对应的全局最优值σi_best。 1)更新当前观测矩阵x与混合矩阵Λ。 2)根据2.1节,通过正则化SimCO字典学习算法训练字典D,并使用MTD方法根据D求解字典域Ψ。 4)计算各路信号的σi值与对应的差值Δσi,根据所求的Δσi更新最优值σi_best。 (2)给定当前各路信号的σi与σi_best,动态确定信号分段长度τ: 1)根据式(13)更新当前的目标函数Γ(σ)。 2)根据式(15)更新步长λ与对应的信号分段长度τ。 (3)k=k+1。计算归一化差值Δσni并迭代上述两步直至各路信号均满足0<Δσni<ε时停止迭代过程。 本文实验仿真在Matlab R2017b的环境下进行,实验目的是对比分析本文所提出的动态字典学习的改进SimCO算法与传统SimCO算法在UBSS模型中同一字典域下源语音信号的重构结果,同时进一步与频域稀疏优化方法[14]对比研究源信号在不同稀疏域下的恢复质量。 实验仿真数据选用SiSEC2011提供的3组语音[15]:dev1_female、dev1_male、dev2_female,其中每组数据均包含4路源语音s1、s2、s3、s4,每路语音信号的时长为10 s且采样率为16 kHz,即每路数据有T=160 000个样本点。 在两步法框架中,为研究第二步优化过程中源信号的重构效果,给定一个2×4的混合矩阵如下 (16) 对4路源信号进行混合,可求得2路混合信号x1、x2。 在所提改进算法中,首先通过正则化SimCO字典学习方法训练字典D:对混合信号X进行分帧处理,帧长L=512,重叠长度F=450,形成样本矩阵B∈R512×5148,设置字典更新次数为5,正则项参数μ=0.1,稀疏矩阵Y的稀疏度为5,得到字典矩阵D∈R512×512;进而通过动态优化策略设计分段长度τ:设定初始分段长度τ=1×102及步长λ=3×102,常系数ι=1×103,阈值ε=0.4,并在MTD框架下,将D构造为字典域Ψ;最后根据OMP稀疏重构算法[16]逐段恢复源信号。取一组混合语音dev2_female,应用本文改进算法所求得的语音重构结果如图3所示。 图3 所提改进算法的实验结果 可见,与源信号的时域波形相比,重构源信号在有声波形部分的恢复效果较好,尤其在波形幅度变化较明显及语音段的集中区域,本文算法能够基本实现源语音的盲分离过程,实验结果较为理想。 采用文献[14]中的频域优化算法处理这3组混合语音时,需将时域信号变换至频域进行稀疏重构。首先对混合语音X进行STFT处理,设置帧长为2048,帧重叠长度为717,并选用Hanning窗进行加窗操作,从而得到频域稀疏信号;在频域根据稀疏优化算法重构信号,最终通过逆STFT处理实现源语音恢复。 对STFT处理后的两路混合信号虚部作散点图进行稀疏表征分析,可获得3组语音信号在同一混合条件下的频域稀疏情况,如图4所示。 图4 3组混合语音的频域散点 若混合语音的数据分布在频域散点图上呈现较为明显的线性聚集性,则源信号的频域稀疏性较强[17]。可见,dev1_female组的4路语音数据分布均比较清晰,而dev1_male组的4路语音数据分布均比较模糊,dev2_female组的4路语音中有2路数据的线性分布相对明显。 采用传统SimCO算法和本文所提改进算法处理这3组混合语音时,需将时域信号变换至字典域进行稀疏重构。在使用正则化SimCO字典学习方法求得相同的字典矩阵D∈R512×512后,分别在传统算法的固定分段长度τ=2048和改进算法的动态分段长度τ下,构造字典域Ψ,从而逐段重构源信号。 针对3组不同的混合语音信号,表1展示了改进算法与另两种对比算法的重构准确度结果,其中,一种对比算法采用频域稀疏优化算法处理混合语音,另一种对比算法采用基于固定信号分段长度的传统SimCO算法。 表1 不同算法下3组源信号的重构准确度对比 对表1中的3组数据作如下分析: (1)对比同一组语音中3种算法的语音分离结果,可知:传统SimCO算法在字典域的重构准确度较低,而改进算法可动态寻找得到全局重构准确度最高的4路源信号,3组语音中各路信号的最优σ值与传统算法相比可高出约0.9 dB~2.7 dB,且信号在字典域的稀疏性越强,改进算法的重构准确度提高越多;相较于频域优化算法的重构结果,改进算法在各组语音中均能有1~3路源信号的最优σ值高于在频域的重构结果,且最高可相差约1.0 dB。 (2)对比不同组语音在同一算法下的语音分离结果,可知:在频域优化算法中,对照图4可得,信号在频域散点图的线性分布越明显,即信号稀疏性越强,则重构准确度越高;在同一字典变换域中,本文改进算法能够进一步利用信号的稀疏特征并提高信号的重构准确度,且各路信号在频域与字典域的稀疏性相近。 为进一步对比在固定分段长度与动态确定的分段长度下语音信号的恢复效果,定量分析固定较小值τ=100、固定较大值τ=160 000及动态值τ下信号的重构准确度,取其中一组混合语音dev2_female,分别根据传统SimCO算法与改进算法求得重构结果,见表2。 表2 不同分段长度下四路源信号的重构准确度对比 可见,在不同分段长度中信号的重构σ值有所差异:较小值下的重构效果并不理想,而较大值下的重构结果不一定为全局最优,因此固定信号分段长度的求解方法无法确保各路语音均能取得最佳重构精度。 因此,为了进一步统计分析源信号在优化重构过程中的收敛情况,对4路恢复信号的全局最优值σi_best进行均方根计算,并求得每次迭代中4路信号的总体最优值 (17) 利用Matlab的Curve Fitting工具箱拟合3组语音在动态学习算法中分段长度τ与总体最优值σbest的趋势图,如图5所示。 图5 3组语音分段长度τ与σbest的曲线 可见,3组语音信号的τ-σbest变化趋势相似:τ<200时,函数值呈直线增长趋势;当σbest增大至全局最优值附近时,曲线总体平稳且基本收敛[13]。因此所提改进算法适用于具有不同语音特征的语音组,通过动态改变分段长度对各路信号进行优化重构能够得到总体最优解,并有效降低了算法运行成本。 本文基于UBSS场景下语音信号在字典域的稀疏性,依据两步法框架下的CS理论提出基于动态字典学习的稀疏信号重构算法,通过动态选取信号分段长度,探究信号重构结果的变化趋势并优化求解恢复效果最佳的一组源信号。对比本文算法与传统SimCO字典学习算法及在不同变换域中稀疏重构的实验数据,分析可知所提的改进算法能够充分挖掘信号在字典域的语音特征,提高源信号的稀疏重构准确度,改善盲语音分离质量,为信号的稀疏表示方法提供了更多可能性,从而进一步扩大欠定盲源分离模型的应用范围。2 基于动态字典学习的欠定语音信号重构算法
2.1 正则化SimCO字典学习算法

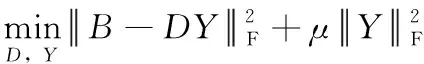


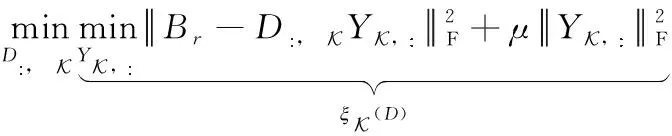

2.2 动态字典学习的稀疏信号重构算法
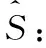
3 实验仿真分析
3.1 所提算法的实验仿真结果
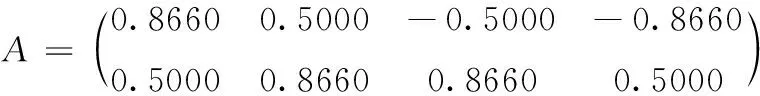

3.2 不同算法的性能对比分析


3.3 不同信号分段长度对恢复性能的影响
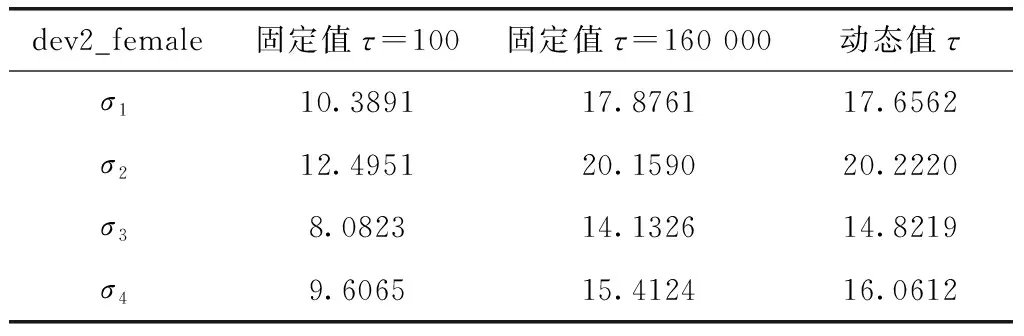
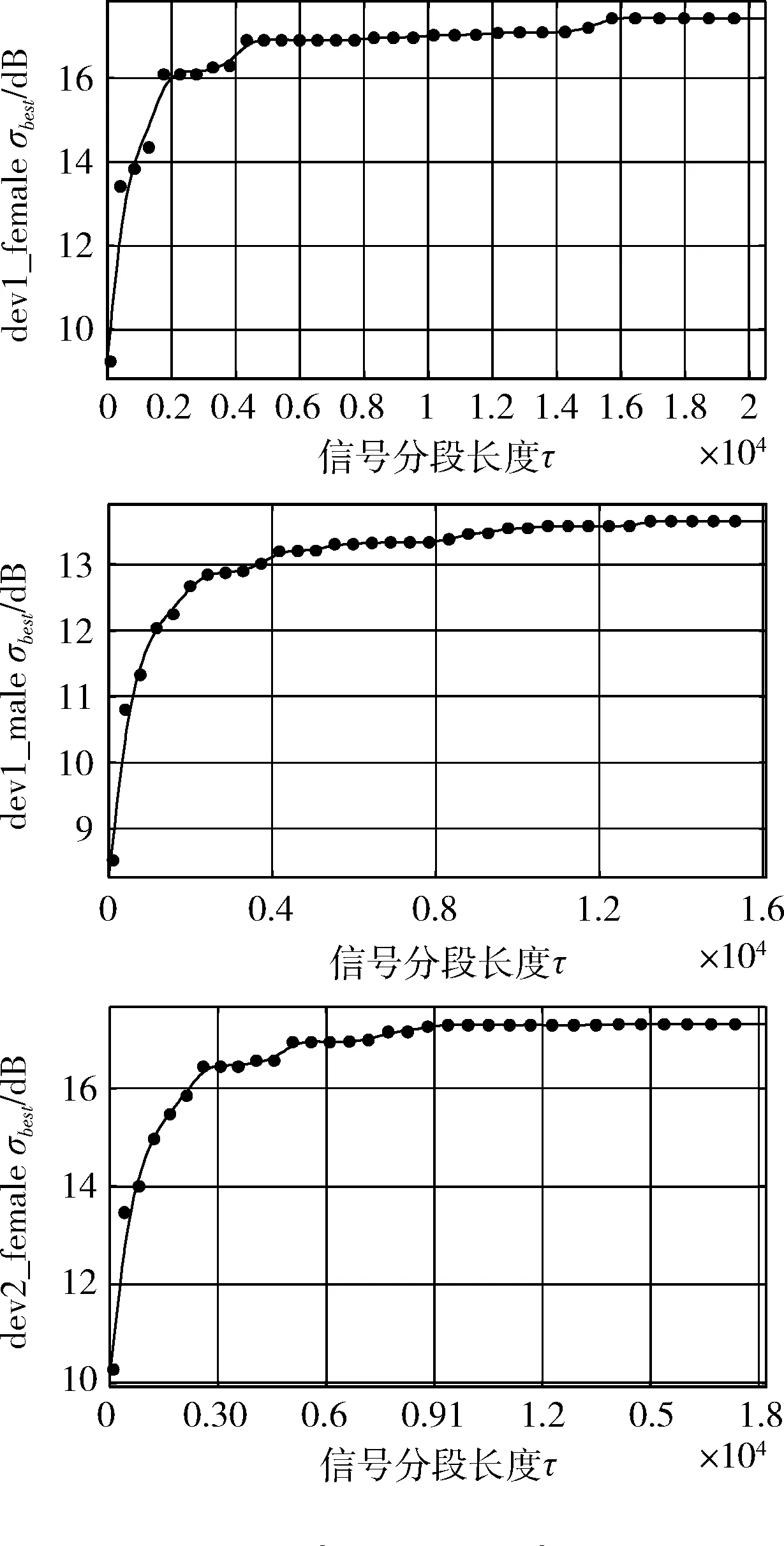
4 结束语
