在杆秤改装密度秤中培养学生质疑创新能力
——以密度秤设计缺陷为例
2022-05-23韩兴富
韩兴富
(山东省滕州市北辛中学,山东 滕州 277599)
明代学者陈献章曾经说过“学起于思,思源于疑”,质疑在学习中的地位不言而喻,质疑创新更是科学思维中最高层次的核心素养之一.在初中物理教学中谈质疑创新不仅仅是指知识与技能方面,更重要的是对事实证据与科学推理等不同形成的知识、观点及结论提出批判性地质疑、检验与修正,从而提出创造性的见解与品格.[1]具体来说表现为善于发现设计仪器缺陷并进行改进,对新颖现象设想与推测并会进行周密论证,探索解决问题的新方法,在问题中鼓励学生用于摆脱思想束缚并进行大胆创新等.[2]因此,培养质疑创新能力是发展科学思维的当务之急,更是提升核心素养的必有路径之一.本文以2021年四川省遂宁市第20题问题(4)为例,对杆秤改装密度秤的设计缺陷提出质疑,并进行创新设计,以此深化质疑创新在科学思维中的核心地位,让提升核心素养的目标不再是一句空话.
质疑背景:[2021年四川省遂宁市第20题(4)]创新科技小组用轻质杆设计制作了测量液体密度的工具——密度秤.其中经防腐处理的合金块重8 N,体积100 cm3,秤砣重2 N,秤纽处O到A端长10 cm.测量时手提着秤纽将密度秤的合金块浸没在待测液体中(不接触容器),调节秤砣位置使秤杆水平平衡,秤砣悬挂处的刻度值为被测液体密度.请解答下面问题(g=10 N/kg):列出秤砣悬挂位置到秤纽O点距离L与待测液体密度ρ的函数关系式,并说明制成的密度秤刻度是否均匀.
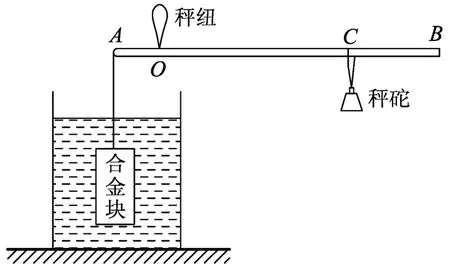
图1
北宋苏轼在《稼说送张琥》中指出“博观而约取、厚积而薄发”,知识的学习只有积累到一定量才会喷发出来,所以要培养学生质疑创新能力,也一定要有大量的知识储备与积累.[3]本文将综合杠杆平衡条件、二力平衡、浮力、液体的密度测量等学科间知识融合在一起,借助对杠杆的改装来测量液体的密度.解决这样的综合性问题需要一定的知识储备与积累,更是实现质疑创新的必要前提,凸显了以知识建构为基础下对物理问题不断质疑创新,发现原有物理问题中知识的缺陷性、局限性、不合理性等,找出新的探究问题与方案.在质疑创新思维下运用科学探究及创新思维来对原物理问题中知识进行改进创新,从而有效培养学生对物理问题的质疑创新的核心素养.
1 质疑杆秤改装密度秤的设计缺陷
关于自制密度计与改装密度秤在众多文献中有所体现,如以综合实践活动为基础对制作的简易密度计进行反思与评价[4]、以项目学习为指引谈自制的简易密度计的刻度是否均匀进行科学分析[5]等.这些都能实现对不同液体的密度测量,现在的初中物理教学倡导的是STEM教育下的学科间综合应用,能够实现STEM教育的基础在于物理学科中不同板块知识的有机整合,避免碎片化知识的产生.如本题中杆秤改装密度秤就是物理学科中多个力学知识有机整合的体现,实现了以学生认知为基础,通过对杆秤改装密度秤的质疑并发现设计缺陷,同时会对改装密度秤进行创新,让设计缺陷成为学生参与物理实验的宝贵资源,进而提升学生科学思维能力,实现核心素养的逐步提升.[6]
本题中前3问属于杆秤改装密度秤的问题,是利用杠杆平衡条件,借助浮力知识求解某一特定条件下A处拉力、液体的密度等,属于简单问题.本文重点以问题(4)为背景,对杆秤改装密度秤的设计缺陷进行质疑,达到巩固知识,提升学生科学思维的能力.
为了研究改装密度秤中L-ρ的函数关系式,设杆秤秤砣悬挂点C到秤纽O的距离为L,合金块浸没在液体的密度为ρ,则根据杠杆平衡条件,浮力、二力平衡等知识得出关系式(G金-ρg V排)·LOA=FC·L,代入数据化简得
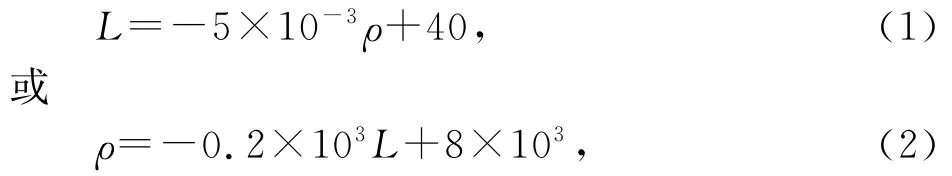
其中L的单位为cm,ρ单位为kg/m3.
现在对杆秤改装密度秤的刻度进行刻画:由上述关系式(1)进行分析.这是一个单调减函数,随着液体的密度ρ逐渐增大,秤砣悬挂点C到秤纽0的距离L逐渐减小.当ρ=0,即合金块没有浸没在液体中时,L=40 cm;当ρ=8×103kg/m3时,L=0.如图2所示,在杆秤上刻画液体密度的总长度L=40 cm,液体密度的范围为Δρ=8×103kg/m3,即0.2×103kg·m-3/cm,再根据初中物理各版本教材(如人教版、苏科版、沪科版等)中列举的常见液体密度值(常温常压下)可以发现,平时我们遇见的液体密度值范围大约为Δρ=(0.7~1.8)×103kg/m3(水银的密度ρ水银=13.6×103kg/m3).于是在杆秤OC(放大)上刻画常见液体的密度值,这里省略一些不常见的液体密度值,如图2中对杆秤刻度线进行放大,这样初看起来改装的密度秤是符合规范且合理的,但是从认知心理学和测量工具设计规范等角度看还是存在设计缺陷的,具体表现在以下几点.

图2
1.1 与认识问题的习惯不相符合
在认识物理规律形成的函数关系式y=f(x)中,如果自变量x在变大的同时,应变量y也在相应地变大,那么由这样的物理规律形成的仪器很容易被人们接受,如温度计、弹簧测力计、电流表、电压表等.相反,如果自变量x在变大的同时,应变量y在相应地变小,由这样的物理规律形成的仪器学生不太习惯,极易产生错误的判断,形成错误认知,如密度计等.本文中改装的密度秤的L-ρ的函数关系式(1)式是一个单调减函数,当ρ=0时,L=40 cm,此时杠杆中密度刻度线最长;当ρ=8×103kg/m3,液体密度最大时,相当于合金块悬浮于液体中,L=0,此时杠杆中密度刻度线直接位于秤纽处.从以上规律可以看出,液体密度越大,L越短,这种刻画刻度线的方法极易导致学生对液体密度产生错误的判断.
再者这种密度秤测量液体密度的范围为ρ液=(0~8.0)×103kg/m3,如果液体密度ρ液>8.0×103kg/m3,杆秤A处下的合金块将在液体中上浮直至漂浮.这样将无法测量液体密度,也就失去了密度秤测量液体密度的意义.
1.2 设计出现头重脚轻的不规范现象
根据上述改装的密度秤的ρ-L的函数关系式(2)式可以看出,液体密度ρ与秤砣悬挂点C到秤纽O的距离L成线性关系(符合y=kx、或y=kx+b),所以这个改装密度秤的刻度是均匀的.只是常见的液体密度值往往只集中在杠杆刻度线(30~40)cm处,如图2所示,如ρ水=1.0×103kg/m3在35 cm刻度线处,ρ酒精=0.8×103kg/m3在36 cm刻度线处等,至于杠杆中(0~30)cm刻度线几乎没有液体密度值.这样导致杆秤刻度出现头重脚轻的不规范现象.再者,根据上述对单位长度下液体密度变化范围0.2×103kg·m-3/cm可以看出,在(30~40)cm范围,即杆秤中长度为10 cm的范围内刻画常见液体密度变化范围Δρ=2×103kg/m3.这样往往导致密度秤的分度值稍大,不够精确,误差较大.
2 质疑创新:对杆秤改装密度秤的创新设计
原题中杆秤改装密度秤之所以在设计上不符合人们习惯,主要原因在于杆秤A处下的合金块悬挂在液体中,利用称重法(FA=G金-ρg V排)将FA与ρ紧密联系在一起,再在杠杆平衡条件(FA·LOA=FC·L)下实现了将液体密度ρ转变成L的杆秤密度秤,只是L-ρ的在变化关系上符合单调减函数.为此,为了实现对杆秤真正意义上的改装,避免密度秤在设计上的缺陷,特进行如下创新设计.
对杆秤改装密度秤的创新设计依然以原题中杠杆(图3)为基本器材,只是将杠杆A处悬挂的合金块浸没在液体中,改换秤在A处用细线悬挂一个100 mL的空桶,利用杠杆直接测量盛放在空桶中液体的重力G,进而测量处液体密度ρ,如图3所示,具体的创新设计过程如下.

图3
器材:轻质杠杆、100 mL空桶、秤砣mC、细线、刻度尺.

过程:(1)确定0点位置.将杠杆在秤纽O处悬挂起来,在杠杆A处用细线悬挂空桶,将秤砣悬挂在C处时保持水平平衡,根据杠杆平衡条件得出mAg·LOA=mCg·L0C,此时的C点即为液体密度为0的位置.


分析:于是可根据上述关系式(3)画出ρ-L的函数关系图像,ρ与L成线性关系,因此,密度秤的刻度也是均匀的;并对密度秤的杆秤上进行常见液体密度值进行刻画,同时从关系式(3)(单调增函数)可以看出,密度秤的刻度设置符合认识习惯,即液体密度值越大,L越长.
为了使密度秤能够精确测量常见液体密度值,避免出现头重脚轻、精确度不高等不规范现象,需要对密度秤中部分数据设置进行设当改进.
(1)减小密度秤能够测量的范围(即Δρ=(0~2.0)×103kg/m3):根据上述关系式(3)可知,要减小测量液体密度的范围,可以减小秤砣质量mC、或增大空桶中盛放液体体积V(选用容积更大的空桶)、或增大LOA长度、或减小秤砣质量mC的同时增大空桶中盛放液体体积V与LOA长度的乘积.

结论:通过以上对杆秤改装密度秤的创新设计分析,将待测液体盛放到空桶中并尽量增大液体体积、增大LOA长度,同时减小秤砣质量mC.这样可以避免原题中杆秤改装密度秤的设计缺陷,达到改装最优化设计,是质疑创新在改进方法上的典型应用.这样可以避免将改进方法知识化进行传授,有利于科学思维能力的培养.
如果需要增大密度秤的量程,可以将密度秤设计成双秤纽,如图4所示.这样的密度秤既可以精确测量常见液体密度,又可以测量密度大的液体,可谓是一举双得.
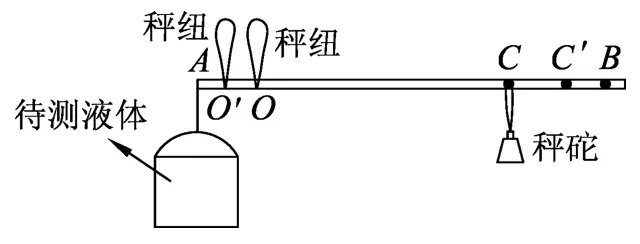
图4
3 创新拓展:将水平密度秤变成竖直漂浮密度计
测量液体密度不仅可以使用上述改装密度秤,而且还可以自制密度计测量液体密度,这样可以将质疑创新能力上升到一个新的高度,这样不仅实现对知识与技能方面的质疑创新,更重要的是探索测量液体密度的新方法,在改进问题中鼓励学生摆脱思想束缚并进行大胆创新,从而唤醒学生进行质疑创新的内驱力,如2021年北京市中考物理试题第12题、2021年广西壮族自治区贵港市第19题、2020年北京市中考物理试题第15题等.这些也都从不同角度对自制密度计进行了创新设计.
例题.(2020年北京市中考物理试题第15题)某同学在粗细均匀的木棒上缠绕一些细铜丝,制作简易密度计A,如图5(甲)所示.将A依次放入一系列密度已知的液体中,每次当A在液体中处于竖直漂浮状态时,在木棒上标出与液面位置相平的刻度线及相应密度值ρ,并测量木棒浸入液体的深度h,再利用收集的数据画出ρ-h图像,如图5(乙)中图线①所示.该同学继续选用了与A完全相同的木棒,并缠绕了不同质量的铜丝制作简易密度计B.将B同样依次放入一系列密度已知的液体中进行实验,得到图乙中图线②.他进一步研究发现对同一密度计浸入液体的深度h和对应密度ρ的乘积不变.铜丝的体积可以忽略,下列说法正确的是
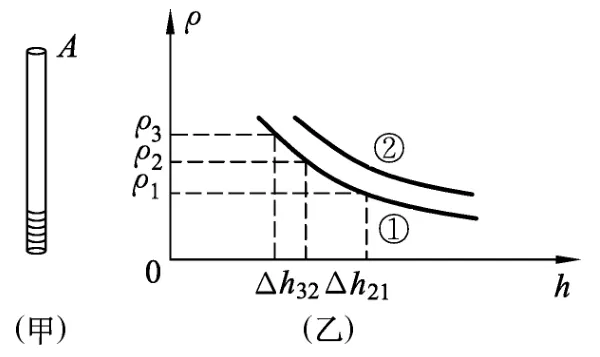
图5
(A)上述实验中密度计A在不同液体中漂浮时,浸入的深度h越大,受到的浮力越大.
(B)密度计B上越靠近铜丝的位置,其刻度线对应的密度值越小.
(C)密度计A上缠绕铜丝的质量小于密度计B上缠绕铜丝的质量.
(D)若图5(乙)中ρ3-ρ2=ρ2-ρ1,则密度计A上ρ3与ρ2刻度线的间距大于ρ2与ρ1刻度线的间距.
在对实验装置改进过程中的质疑创新还体现在实验方案以及实验操作过程中的质疑,推陈出新,体现创新设计的基本理念.[7]将水平密度秤变成竖直漂浮密度计是对改装密度秤的创新拓展,同一个密度计由于下端配重不同可以制成不同量程的密度计,将此时制成的量程不同的密度计进行对比分析,是对质疑实验方案以及实验操作下进行创新设计的又一生动体现.
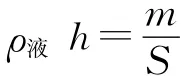
4 结束语
对物理问题的质疑是培养创新思维的摇篮,创新是对物理问题质疑的终极目标,更是落实核心素养的关键因素之一,因此,教师要能提出引起学生质疑创新的问题,更要科学对待学生提出的异想天开的问题,这样才能在质疑创新的道路上越走越远,培养科学思维能力,让提升核心素养的目标不再是一句空话.
