物体连滚带滑问题的多种解法探析
——以第38届全国中学生物理竞赛预赛第8题为例
2022-05-23曾小江
曾小江 曾 伟
(四川外语学院重庆第二外国语学校,重庆 400065)
2021年第38届全国中学生物理竞赛预赛第8题是一道关于均质小球连滚带滑问题.解决连滚带滑问题不能将物体视为质点,应视为另一理想模型——刚体.[1]均质刚体连滚带滑问题蕴含丰富的物理思想和方法,是考查学生熟练掌握物理规律,灵活应用物理知识一类典型问题.通过对本题的分析求解,希望能加深学生对连滚带滑问题的理解,提高学生运用物理规律多角度分析解决实际问题的能力.
1 原题及分析
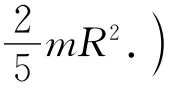
解析:由题意可将小球的运动分为如图1所示的3个运动阶段.
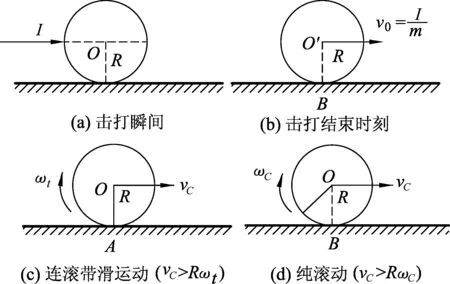
图1 小球运动示意图
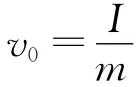
第2阶段——连滚带滑过程.小球与桌面的接触点A的速度vA是质心平动速度vC和绕过质心轴转动速度Rωt的合速度,即vA=vC-Rωt.在小球纯滚动之前始终有vC>Rωt,接触点A相对桌面向右运动,小球在接触点一直受到大小为f=μmg,方向水平向左的滑动摩擦力,摩擦力使平动减速,对质心轴的力矩使小球具有恒定的角加速度α,角速度从0开始均匀增加.小球的运动为质心向右做匀减速直线运动和绕过质心轴顺时针加速转动的叠加,即是连滚带滑运动.
第3阶段——纯滚动过程.当小球与桌面的接触点A的速度满足vA=vC-Rωt=0,即vC=Rωt时,小球开始纯滚动.不计球与桌面的滚动摩擦,小球在水平桌面的运动将不受摩擦力作用,小球将保持以平动速度为vC且绕过质心转轴角速度为ωt的纯滚动运动状态.
以下求解均以击打结束时刻为计时起点,来分析求解小球的运动.
2 多种解法探析
解法1.运用质心运动定理和转动定理求解.
对小球运用质心运动定理有

得aC=μg,方向与质心运动方向相反.
小球质心做匀变速直线运动,由速度公式有vC=v0-aCt,即

以绕过质心的轴为转轴,由转动定理有

由角速度与角加速度的关系ωt=ω0+αt,得

小球与桌面接触点的瞬时速度

将(2)、(4)式代入(5)式得
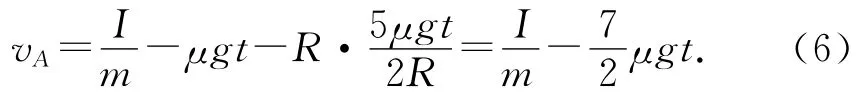
开始纯滚动时接触点A的速度为0,即

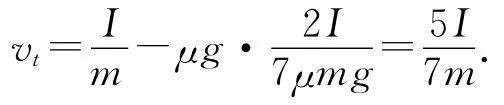
点评:根据小球的受力和运动情况,将小球的连滚带滑运动分解为质心向右的匀减速直线运动和绕过质心轴顺时针加速转动.从动力学的角度运用质心运动定理求出质心的平动加速度aC.运用转动定理解出小球绕质心转动的角加速度α.应用运动学公式求出t时刻质心平动的瞬时速度vC和绕质心轴转动的角速度ωt,而小球与桌面接触点的瞬时速度为vA=vC-Rωt,可得出接触点瞬时速度的表达式.再利用纯滚动的条件vA=0,即可求得从击打结束到小球开始纯滚动的时间和此时的质心速度.此解法能清晰描述连滚带滑运动全过程的物理特征.
解法2.运用动量定理和冲量矩表述的角动量定理求解.
设小球开始纯滚动时质心速度为vt,从击打结束到转变成纯滚动历时为t,以水平向右为正方向.
对小球应用动量定理有

其中f=μmg,I=mv0.
选择过质心且垂直运动纸面的轴线为转轴,由冲量矩表述的角动量定理有

当小球开始纯滚动时有

由(1)—(3)式可解得
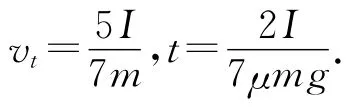
点评:将小球的连滚带滑运动分解为随质心的平动和绕过质心轴的转动.对小球随质心的平动运用动量定理,绕过质心轴的转动运用角动量定理,只需关注小球质心的初末速度和绕过质心轴转动的始末角速度,无需考虑小球运动的演化过程,简化了解题思维过程,是处理物体连滚带滑运动的一种常用方法.
解法3.运用角动量守恒定律求解.
选择过小球与桌面的接触点O且垂直于纸面的轴线为转轴,以垂直纸面向里为角动量的正方向,在运动过程中小球相对于过O点转轴的力矩为0,小球对过O点转轴的角动量守恒.小球对过O点转轴的角动量为质心相对于O点的角动量与绕质心轴的角动量的矢量和.
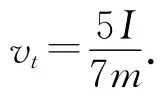
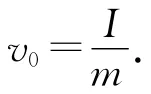
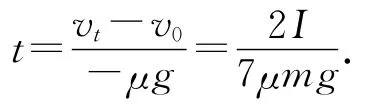
点评:根据物体的受力情况,若能选取合适的转轴(或参考点),物体相对于该转轴的合力矩为0,则相对于该轴(或参考点)物体的角动量守恒,选取物体相对于该轴(或参考点)的初末状态角动量,运用角动量守恒定律,可直接求出物体的运动状态参量,简化了解题过程.需要注意的是,物体相对于转轴的角动量为物体质心相对于该轴的角动量与物体绕质心轴角动量的矢量和.
解法4.运用功能关系求解.
对小球质心的平动由质心运动定理有
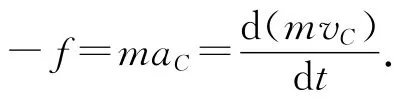
设从击打结束到开始纯滚动小球质心沿相对于桌面的位移为s,对上式两边积分得
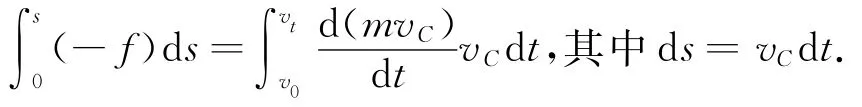
由积分可得
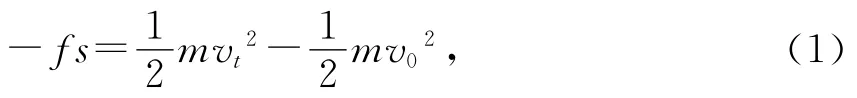
此式表明小球随质心平动时,摩擦力所做的功等于小球平动动能的变化.

式中fRθ为小球绕过质心轴转动时摩擦力所作的功.此式表明小球绕过质心轴转动时摩擦力所作的功等于小球绕过质心轴转动动能的变化.
结合(1)、(2)两式,小球连滚带滑过程的功能关系为

小球随质心平动的位移

小球绕过质心轴的转轴转过的角度

从击打结束到开始纯滚动的时间t的解答过程同解法3.
点评:在本题的连滚带滑问题中,小球质心平动速度vC大于绕过质心轴转动速度Rωt(即vC>Rωt),在质心平动方面,滑动摩擦力做功(-fs)使物体平动动能减少;在绕过质心轴转动方面,滑动摩擦力做功(fRθ)使物体转动动能增加,滑动摩擦力做功实现了物体平动动能向转动动能的相互转换,但总功为负值,使物体总动能减少.根据功能关系,滑动摩擦力做功等于物体动能的变化,列式可解出小球纯滚动时的速度.
值得注意的是,上述各种解法都必须以分析清楚物体运动的初末状态、受力情况和运动约束为前提.滑动摩擦力的方向与物体接触点的速度方向相反,物体接触点的速度是质心平动速度vC和绕过质心轴转动速度Rωt的矢量和,即v=vCRωt.根据物体接触点的速度方向确定物体在接触点所受滑动摩擦力方向的方法:[2](1)若vC>Rωt,物体接触点的速度方向与质心速度方向相同,滑动摩擦力方向与质心速度方向相反;(2)若vC<Rωt,物体接触点的速度方向与质心速度方向相反,滑动摩擦力方向与质心速度方向相同;(3)若vC=Rωt,物体接触点的速度为0,物体纯滚动,不受滑动摩擦力作用.
3 总结
综上所述,对于物体随质心平动和绕过质心轴转动的连滚带滑运动问题,可从4个角度进行分析求解:(1)从运动学和动力学的角度运用质心运动定理和转动定理进行求解,可清晰的描述运动变化的全过程;(2)从动量定理和角动量定理的角度,对质心的平动运用动量定理和对绕过质心轴的转动运用角动量定理进行求解,只需关注运动的初末状态;(3)根据物体的受力情况,若能选择合适的转轴(或参考点),使各力对该轴(或参考点)的力矩为零,运用角动量守恒定律求解,可简化解题过程,计算简单,但此法只能在选取到合适的转轴条件下使用;(4)在连滚带滑运动中,滑动摩擦力所做的功是物体随质心平动时摩擦力所作的功和物体绕质心轴转动时摩擦力所作的功的代数和,从功能关系的角度,运用动能定理求解,只需明确物体初末状态的动能.
以上4种解法涉及的知识几乎涵盖了力学的大部分主干内容,在解决问题的思路上实现了从常规思维向高阶思维的转化,充分展现了运用物理规律解决生活实际问题上方法选择的灵活性、多样性,对启发学生运用物理规律多角度探索生活中的实际问题,提高学习兴趣都很有意义.
