再入飞行器深度确定性策略梯度制导方法研究

郭冬子, 黄 荣, 许河川, 孙立伟, 崔乃刚,*

(1. 哈尔滨工业大学航天学院, 黑龙江 哈尔滨 150001; 2. 北京控制与电子工程研究所, 北京 100038;3. 中国兵器工业集团航空弹药研究院, 黑龙江 哈尔滨 150030)

0 引 言

从1911年Thorndike提出效用法则,阐述了生物学上的情景增强与动作再现之间的关系,到1954年Minsky首次实现了“试错学习”,并在1961年提出“reinforcement learning”概念,再到1957～1960年Bellman和Howard提出强化学习框架基础——马尔可夫决策过程(Markov dec process, MDP)及其策略迭代方法,为强化学习奠定了扎实的现代理论研究基础;1956～1994年,动态规划、时间差分、Q-learning、Saras等算法相继被提出,进一步丰富了强化学习的内涵和应用手段,强化学习逐渐进入了理论研究与实际应用的“高并发”热潮;1992～2018年,不仅有经典的神经动态规划、置信上限树、Deep-Q-Network、异步优势执行器评价器(asynchronous advantage actor-crific, A3C)、分布式策略优化(distributed proximal policy optimization, DPPO)和深度确定性策略(deep deterministic policy gradient, DDPG)等算法,还有世人尽知的Backgammon游戏、AlphaGo、AlphaGo Zero和人工智能(artificial intelligence, AI)参与的DOTA比赛等,强化学习已经逐步深入到了社会发展的各个行业[1]。

再入飞行器在稠密大气层内飞行时,由高马赫引起的气动加热、气动过载和动压影响严重[2],传统跟踪制导方法难以充分利用飞行器的剩余飞行能力以满足终端约束;可采用强化学习方法,将再入飞行器视作智能体agent,通过与飞行环境的不断交互,寻找最佳的制导系统模型,以在线确定最佳制导指令,从而有效克服再入飞行过程中内外扰动与模型不确定性引起的偏差,满足终端约束要求。

国内外相关学者已经就强化学习方法在飞行器轨迹优化与制导控制领域中的应用问题,进行了广泛地研究。文献[3]提出了一种基于强化学习与神经网络的轨迹优化智能决策算法,解决了再入轨迹优化算法在建模偏差或者扰动下任务适应性较差的问题。文献[4-10]针对飞行器姿态稳定控制问题,采用了actor-critic、PILCO (probabilistic infe-rence for learning control)等方法进行了复杂干扰条件下的控制器设计与控制参数优化研究。文献[11]针对传统预测校正算法迭代预测再入轨迹时占用大量计算资源的问题,提出了一种基于actor-critic强化学习的跨周期迭代再入飞行器预测修正制导方法,对初始条件和飞行参数的不确定性具有良好的适应性,但其制导参数存在周期性相互影响,并且攻角剖面给定,难以最大程度地利用再入飞行器的剩余飞行能力。文献[12]提出了基于进化算法与强化学习算法的路径规划方法,解决了有效探索和超参数敏感等动态规划问题,但针对的是简单的“小车爬坡”和“月面末段着陆”等简单动力学问题,并不涉及三维空间中受复杂约束条件的再入飞行轨迹规划问题。文献[13]提出了一种基于深度强化学习的航迹规划策略自学习方法,能够引导无人飞行器在未知飞行环境中安全无碰地到达目的地,但并未针对飞行器动力学模型和复杂飞行约束条件进行充分考虑。文献[14]研究了采用深度强化学习方法生成过载指令以最短时间到达目标,但忽略了引力的影响,飞行器动力学模型较为简单。

本文针对再入飞行器复杂动力学模型和飞行约束问题,利用DDPG强化学习方法,在三维连续空间中将再入飞行器制导规划问题转化为已知当前状态和动作的后续最佳动作与策略的寻找问题,通过大量偏差样本下的离线网络学习,构建满足在线性能指标要求的剖面参数调整网络,最后通过极限拉偏仿真,证明了制导方法的有效性。

1 数学模型

1.1 动力学模型

本文研究对象为大气层内无动力再入飞行器,为更方便地表征飞行器运动状态,在位置坐标系(以地心为原点,Xp轴在飞行器轨道平面内并指向飞行器位置方向,Yp轴与飞行器所处位置处的纬线相切)下建立动力学方程[15],如下所示:

(1)

(2)

式中:CL和CD为升力系数和阻力系数,可由攻角α和马赫数Ma插值气动文件进行求取;q为动压;Sref为飞行器气动参考面积。

(3)

1.2 约束条件

再入飞行器飞行过程受到热流密度、过载、动压等复杂过程约束限制[16]。

(1) 热流密度约束

采用热流密度计算公式:

(4)

式中:Rh为飞行器头部曲率半径;Cf为与飞行器特征相关的常数;海平面大气密度常量ρ0=1.225 kg/m3。

(2) 过载约束

为保证飞行器结构设备稳定工作,气动力总过载需要限定在一定范围内:

(5)

式中：g为重力加速度；m为质量。

(3) 动压约束

动压对控制系统横侧向的稳定具有重要影响,需小于限定阈值:

(6)

(4) 终端约束

根据能量管理或末制导要求,终端目标状态需满足如下约束:

(7)

1.3 控制量剖面

攻角α和倾侧角σ为再入飞行器的控制量,攻角设计[17]为与最大热流密度约束和过载约束相关的随速度变化的剖面形式:

(8)

式中:αmax为与气动特性和热流密度相关的最大攻角；α2为滑翔飞行段的攻角,通常取为最大升阻比对应攻角；V1、V2为分段处对应速度大小。

设计倾侧角大小|σ|为速度V的函数:

(9)

式中:V0为当前速度大小;σ0为当前状态下满足准平衡画像条件的倾侧角大小;Vf为飞行终端速度大小;σf为终端速度状态下满足准平衡滑翔条件的倾侧角大小;σmid为速度中点状态对应的待规划倾侧角大小。

倾侧角符号则按照经典的航向误差走廊翻转形式给定,后续将基于本节描述的攻角剖面和倾侧角剖面形式,采用强化学习方法调整剖面参数。

2 制导系统设计与关键算法

2.1 制导系统设计

再入飞行过程中,攻角/倾侧角剖面对飞行器的制导性能影响关系较为复杂,传统制导方法通常根据专家经验离线调整设计并固定飞行剖面,难以适应强扰动下的飞行环境[18]。本文采用强化学习方法,根据飞行状态自适应调整制导剖面参数。

考虑到各剖面参数均为在一定区间内的连续量,若采用深度Q网络方法,则需要将参数离散化,产生维度灾难[19]。为此,本文采用深度确定性策略梯度方法[20],将剖面参数调整视为连续动作空间强化学习问题。建立actor-critic架构的智能体,actor部分根据状态st进行决策输出动作μ(st),critic部分则根据状态st及动作at估计Q值。对于每一部分,分别设置两个结构相同,参数不同的神经网络,即online网络与target网络。

在训练过程中,智能体的online-actor网络生成剖面参数,并添加动作噪声,完成对攻角及倾侧角剖面参数的调整;飞行器基于调整后的剖面生成攻角、倾侧角指令并输入动力学模型中;动力学模型返回飞行器下一步状态及反映制导结果的剩余航程、速度误差。将状态转换过程信息,即原状态-动作-奖励-转换状态[st,at,rt,st+1]存入经验池。按照设定的训练频次,随机抽取经验池中的样本,训练online网络并对target网络参数进行软更新。训练过程如图1所示。

训练完毕后,提取智能体的online-actor网络参数并固定下来。在飞行过程中根据当前状态,预测输出调整后攻角/倾侧角剖面参数,飞行器即可根据剖面输出攻角/倾侧角指令,进行后续飞行。此外,为进一步提高飞行控制指令的合理性与飞行轨迹的平滑性,在由智能体网络得到攻角指令αnet的基础上,进一步加入速度与飞行路径角反馈,并加入角速率限幅:

αh=αnet-kVγ

(10)

(11)

式中:k为调整系数,通常为一较小的非负常数;αh为速度与飞行路径角反馈得到的攻角指令;αup为上一步实际攻角指令;εα为角速率限幅,可取5°/s。

2.2 再入制导问题的强化学习要素

(2) 强化学习的动作量为倾侧角剖面参数σmid及攻角剖面参数α2,V2,根据前文确定的飞行走廊,动作空间的取值范围为σmid∈[6°,70°],α2∈[8°,16°],V2∈[3 500 m/s,4 500 m/s]。

(3) 对于再入制导问题而言,调整剖面参数的主要目标是减少终端剩余航程误差及速度误差。因此,当飞行器滑翔段飞行结束时,可将终端剩余航程误差及速度误差的平方和的相反数作为惩罚项:

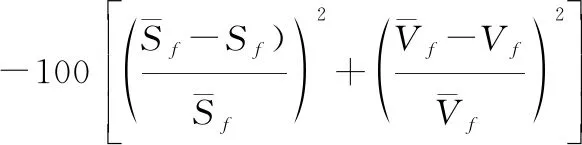
(12)

为了弥补奖励函数过于稀疏的问题,在其他时刻,过程奖励函数如下:

(13)

2.3 强化学习关键算法

在强化学习训练过程中,智能体采用online网络产生动作与环境交互,考虑到DDPG方法中actor网络为确定性策略,若智能体直接采用actor网络输出的动作,将减弱智能体探索动作空间的能力,易陷入局部最优。为此,一般在训练过程中,需对actor网络产生的动作添加噪声作为智能体的动作输出[21]。对于飞行器再入制导这样的连续控制问题,若动作噪声完全随机,易导致各步动作差别较大,不符合真实物理过程。为此,在进行强化学习训练时,采用具有自相关特性的Ornstein-Uhlenbeck过程[22]作为动作噪声:

dxt=κo(ηo-xt)dt+σodWt

(14)

式中:κo,ηo,σo均为常数;Wt为标准随机维纳过程。自相关特性的动作噪声可有效提高网络的探索效果[23]。则训练过程中实际输出的动作为

at=xt+μθoa(st)

(15)

通过带噪声的动作,智能体不断与环境交互,并将状态转换过程信息[st,at,rt,st+1]存入经验池。每当智能体与环境交互sonline步时,从经验池中抽取ntrain个样本进行训练,采用梯度下降法[24]更新online-critic网络的参数θoc及online-actor网络参数θoa:

(16)

式中:rt为当前步的奖励值,若当前步为终端步,则rt=r终端,否则rt=r过程;αc为online-critic网络的学习率,αa为online-actor网络的学习率,ζ为奖励折扣率。每当online网络更新starget次时,软更新各target网络:

(17)

通过以上步骤,在与环境交互过程中,完成对各网络的参数更新。在训练结束后,取出online-actor网络μθoa(s),即可用于再入飞行制导剖面的在线自适应调整。

3 实验与结果

3.1 仿真条件设定

仿真采用通用航空飞行器(Common Aero Vehicle, CAV)再入飞行器,总体参数如表1所示。

表1 飞行器总体参数

为验证方法性能,设计飞行器从赤道上格林尼治零点开始,向正东飞行,相关的任务条件如表2所示。

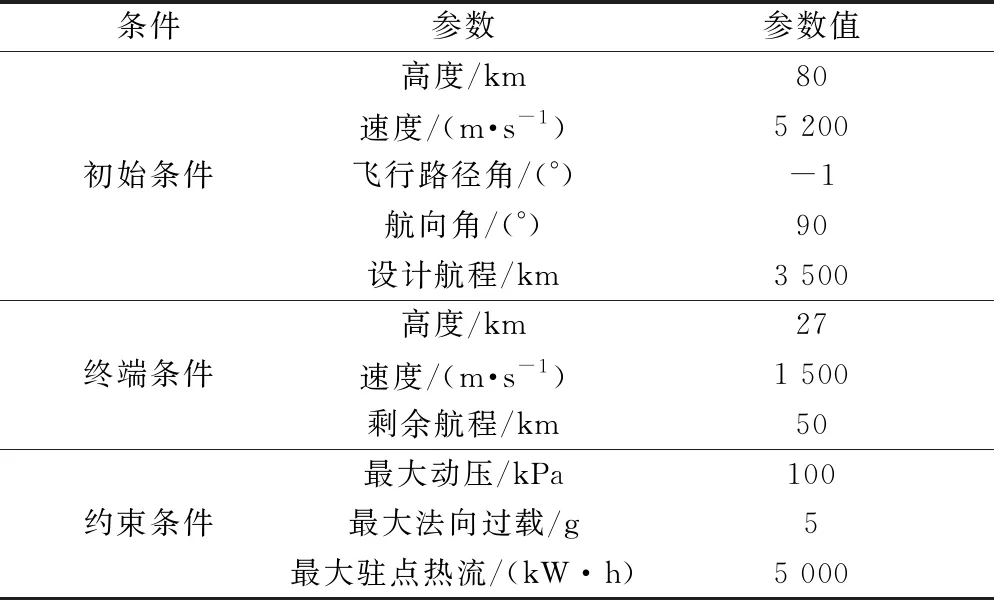
表2 飞行器任务参数列表

仿真步长为0.01 s。仿真过程中,输出倾侧角、攻角指令的制导周期为0.1 s。

再入制导强化学习中,更改剖面参数与环境交互的周期为1 s。actor网络及critic网络隐含层均设置为[200,200,20]的结构,强化学习训练超参数如表3所示。

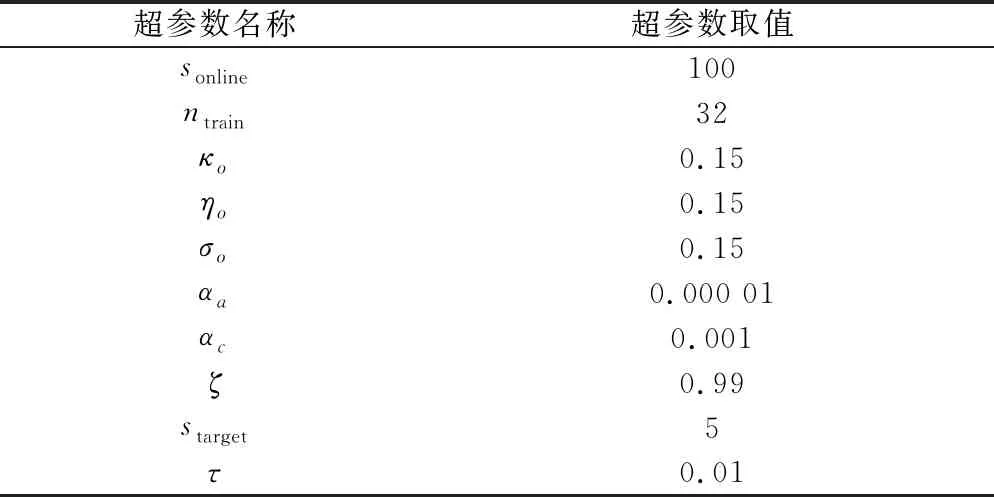
表3 强化学习训练超参数设置

本文进行训练及仿真的计算机配置为intel core i7-10700+Nvidia RTX 2060。

3.2 再入制导智能体的强化学习训练

基于python3.8+tensorflow2.4编写强化学习训练程序。为了提高强化学习智能体的鲁棒性,对环境引入正态分布随机偏差如表4所示。

表4 训练偏差范围

通过1 500次训练,如图3所示,奖励函数逐渐上升,最终完成收敛。

3.3 制导仿真结果

在强化学习训练完成后,获得的智能体online-actor网络可用于飞行器制导的攻角、倾侧角剖面调整。为了验证本文提出的强化学习再入制导方法的精度及计算效率,给定极限拉偏条件:

(18)

分别采用线性二次型调节(linear quadratic regulator,LQR)制导律及强化学习方法进行再入制导仿真,结果如图4～图11所示。

在极限偏差情况下,按照终端高度跳出时,采用LQR制导方法最大终端速度误差为99.326 4 m/s,最大剩余航程误差为1 997.43 m;采用强化学习制导方法最大终端速度误差为34.223 3 m/s,最大剩余航程误差为212.408 m。

在仿真过程中,LQR方法单次输出指令的计算耗时为0.001 1 s,而本文提出的确定性策略梯度方法单次输出指令的计算耗时为0.000 9 s,单次调整剖面参数的计算耗时为0.01 s,可满足计算实时性要求。

4 结 论

本文针对再入飞行器复杂动力学模型和飞行约束问题,利用深度确定性策略梯度方法,在三维连续空间中将再入飞行器制导问题转化为已知当前状态和动作的后续最佳动作与策略的寻找问题,通过大量偏差样本下的离线网络学习,构建满足在线性能指标要求的剖面调整动作网络。实验结果表明:强化学习再入制导方法较传统LQR跟踪制导方法精度更高,能够在初始偏差和过程干扰条件下达到终端速度误差小于35 m/s,终端剩余航程误差小于500 m,满足终端约束要求,并且具有较好的实时性。