基于两相脉冲电流峰值差的开关磁阻电机无位置传感器控制

周 江 迪， 孙 建 忠， 白 凤 仙

(大连理工大学 电气工程学院,辽宁 大连 116024 )

0 引 言

开关磁阻电机(SRM)是一种双凸极式的新型调速电机，基于磁阻最小原理运行，具有结构简单坚固、成本低、能运行于恶劣环境下的优势．然而由于SRM换相需要转子位置信息，控制系统中不得不采用光电编码器等一些位置传感器，这不仅增加了控制成本，而且降低了系统可靠性．因此，无位置传感器的电机控制技术已成为研究的热点和发展的需求[1]．

目前国内外关于无位置传感器控制技术的研究已经有了很大的进展，其中脉冲注入法简单易实施．Pasquesoone 等提出了采用双阈值比较的单脉冲注入法，通过非导通相响应电流值和两个阈值比较，判断切换导通相和检测相[2]．双阈值将电感周期划分成了6个部分，比传统单阈值法[3]有更高的位置精度，能更好应对缺相故障[4]．张磊等在此基础上进行了母线电压波动影响阈值设定的研究，测量了不同母线电压下应设的电流阈值[5]．Ofori等通过对单次脉冲响应电流的积分计算将脉冲注入法拓展到了高速领域[6]．这些方法简单有效，但是阈值都需要提前离线测定．为此，苗盛等采用了两相注入电流斜率比较法[7]，和文献[8]两相注入电流响应值比较法类似，通过比较空闲两相电流斜率的变化来实现换相．这两种方法无须电流阈值，但是电机的导通区间滞后．为了能够提前导通角度，文献[9]采用了两相响应电流值的若干倍关系处作为换相点位置，但是倍数关系值仍然需要事先测定．

综上，单脉冲注入法通常需要事先设定电流阈值，易受转速变化影响．两相脉冲注入法虽无须阈值，但导通区间固定，大转速时容易产生拖尾电流．为此，本文提出一种基于两相响应电流差值的SRM无位置传感器控制方法，通过检索空闲两相响应电流峰值差的极值点，以极大值点作为转子特殊位置更新位置信息，以期在不需要设定响应电流阈值的情况下，拓宽导通相的可导通区间，得到更好的转矩特性．

1 脉冲注入法原理

当对非导通相注入脉冲电压时，由文献[10]可将电机的相电压方程简化成

(1)

式中：U为母线电压，i为电流，L为电感，ω为转子角速度，θ为转子角度．电机转速较低时，旋转电动势可以忽略，且在脉冲周期内能完全放电，式(1)可以进一步简化成

(2)

式中：ip为响应电流的峰值，Δt为一个周期内脉冲注入的时间．

因此在脉冲注入下，绕组电感与响应电流峰值成反比，可以通过检测响应电流峰值间接得到转子位置信息．图1为三相12/8开关磁阻电机的电感图，图2为三相响应电流峰值在不同转子位置处的关系示意图，两图清晰反映了响应电流峰值和电感值的关系．

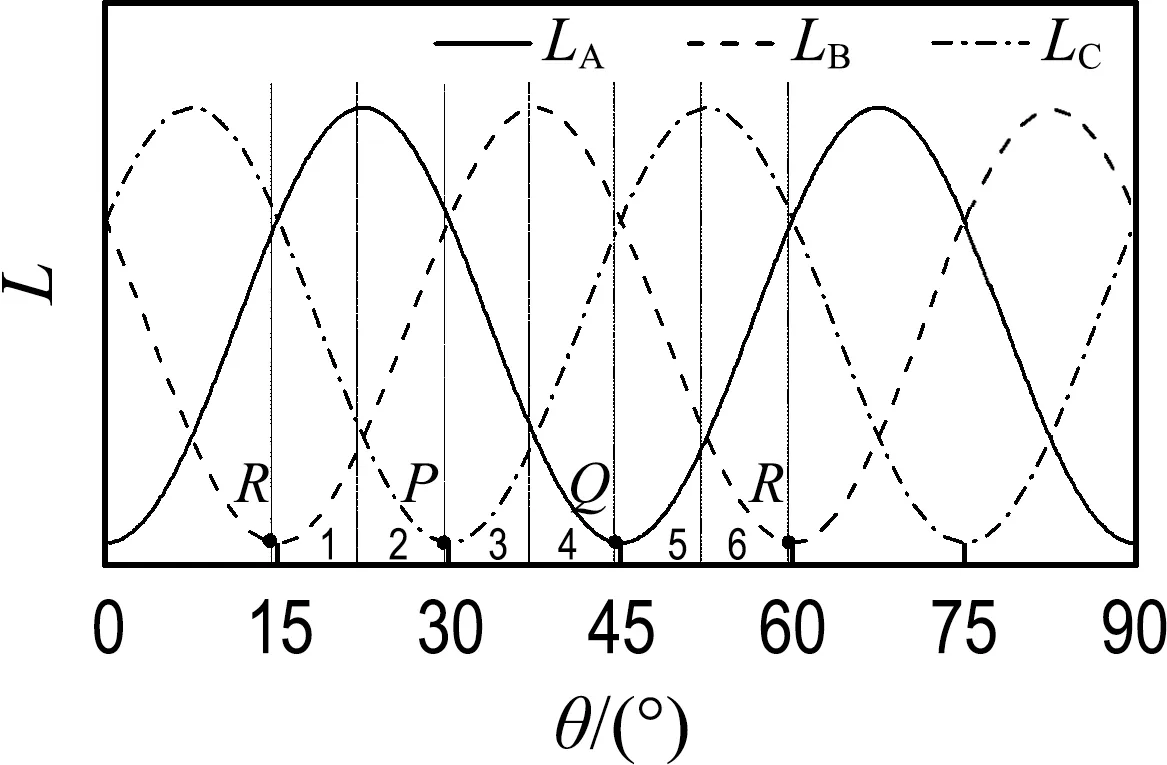
图1 三相电感扇区图Fig.1 Three-phase inductance sector diagram

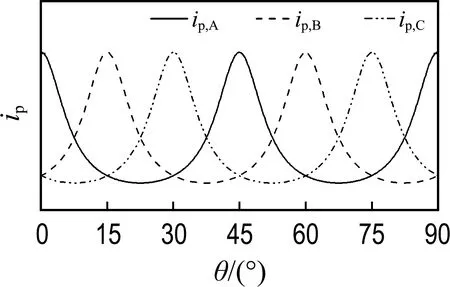
图2 三相响应电流峰值图Fig.2 Three-phase response current peak diagram

2 两相响应电流峰值差法

在脉冲注入的基础上，本文研究了一种应用两相响应电流差值法检测转子位置的控制策略．在电机运行时，向空闲两相注入高频脉冲，实时采样两相响应电流的峰值，由微处理器计算其差值，这些离散的数值经过滤波后可以得到其包络线，它的极大值点作为转子的特殊位置．不同的两相组合能够得到位置偏移的相同包络线，如图3所示，将包络线极大值点记为P、Q和R．因为特殊位置点的间隔角度固定，可以根据间隔时间计算出电机实时转速，更新转子位置并进一步确定转子其他时刻的位置，从而实现电机的无位置传感器控制．

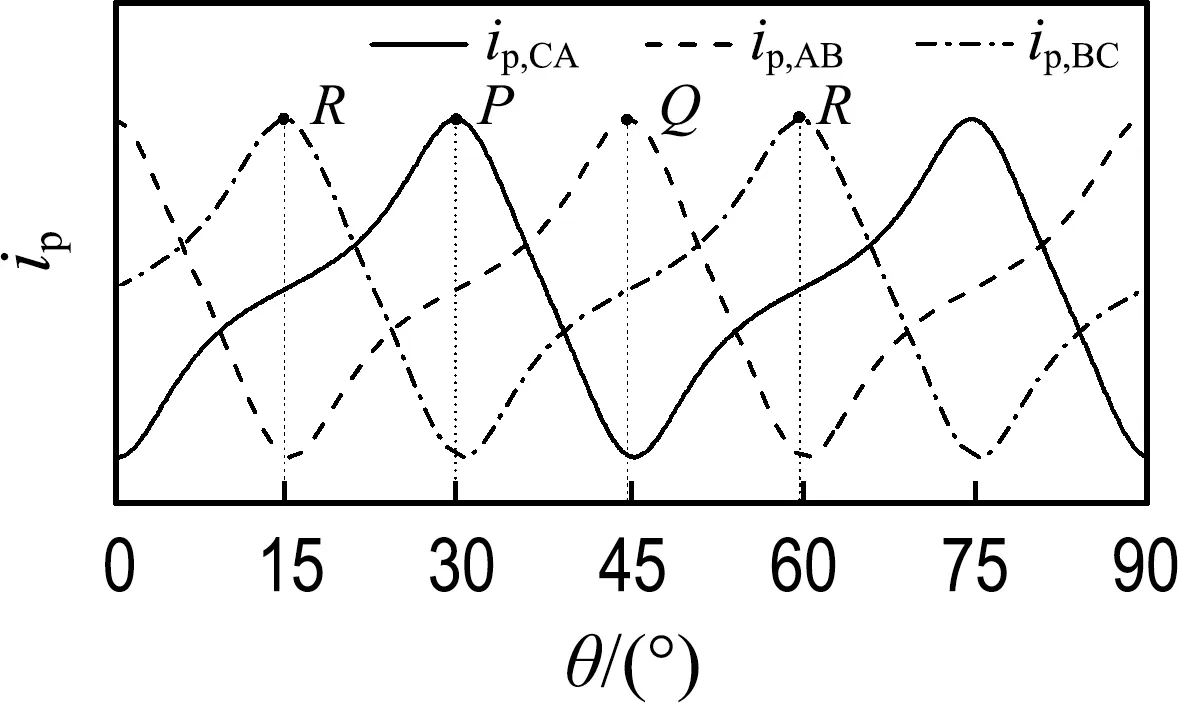
图3 两相响应电流峰值的差值Fig.3 Difference of response current peak between two phases

2.1 校准点转子位置的确定

为简单获得极大值点对应的转子位置，采用文献[11]中展开为傅里叶级数的电感模型．在脉冲注入的小电流下，电感为

L(θ)=L0+L1cos(Nrθ)+L2cos(2Nrθ)

(3)

式中：Nr为转子极数，L0、L1、L2为系数．由式(2)和式(3)算出A、B相响应电流峰值为

(4)

(5)

式中：Δθ为相绕组间电感偏移的位置量．

由此得到A相和B相响应电流峰值的差值，通过求其导数零点算出电周期内极大值点的转子位置，记为θQ，也就是图1和图3中的Q点对应的转子位置．虽然Q点处A相是在电感变化不明显区域，但是B相是在电感快速变化区域，响应电流值作差后的区分度仍然较大．由类似计算可以得到B相和C相、C相和A相响应电流峰值差的极大值点处的位置，为图1和图3中的R点和P点．

当转速增大时，旋转电动势难以忽略，由式(1)可得相响应电流峰值为

(6)

将式(3)的电感模型代入可得各相的响应电流峰值，以A相和B相响应电流峰值的差值为例，对于不同转速，转速最大取到电机的额定转速1 500 r/min，求出的极值点都在[44°，46°]．为了能够快速计算以保证极大值处转子位置跟随转速变化的及时性，在此区间可认为A相电感几乎不随转子位置而变化，即dLA/dθ为0；B相电感为线性变化，即dLB/dθ为常数k．则由式(6)可得B相响应电流峰值为

(7)

A相响应电流峰值仍由式(4)计算，可得到两相响应电流峰值差，对其求导为

(8)

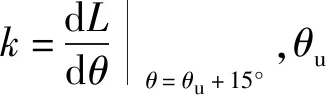
求解式(8)的零点即得转子位置，也可用试解法，以忽略旋转电动势求得的转子位置为基点，前后增减0.1°，以此逼近真正转子位置．

2.2 换相控制方法

利用求得的3个极大值点可以将图1中的电感周期划分成6个均匀区间，如此能清晰有效地控制电机换相和脉冲注入．比如，在1和2区间，B相作为导通相驱动电机，在此区间，C相和A相脉冲响应电流峰值的差值是单调增大的，而在3和4区间这两相脉冲响应电流峰值差是单调减小的．因此，C相和A相响应电流峰值差的极值点可以作为判断换相的条件，当检测到电流峰值差达到极大值点时，切换导通相为C相．运行过程中，为降低开关管损耗，可以减小两相脉冲注入的区间．其他区间依此类推，整个换相逻辑见表1．

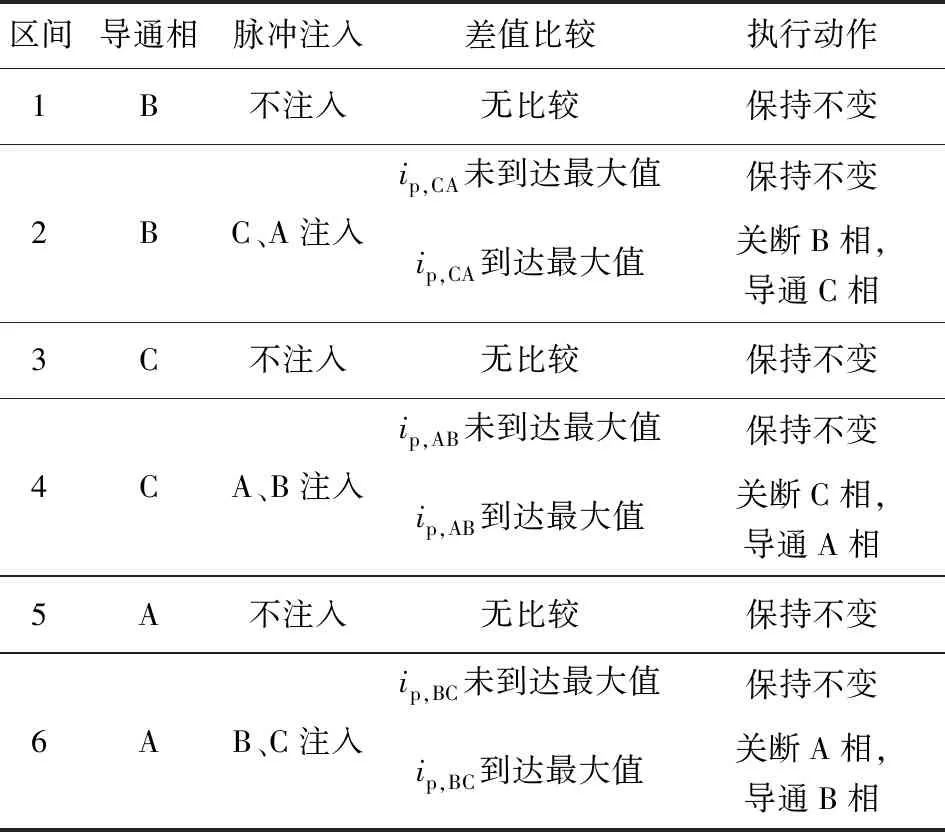
表1 换相逻辑表Tab.1 Commutation logic table

2.3 极大值点的判断

由文献[12]中的误差分析可以知道，采集到

的脉冲电流峰值是离散的，且并非能恰好在特殊转子位置处采样，产生的角度偏移与转速和脉冲周期有关．为了避免此误差和有效地寻找响应电流差的极值点，本文对极值点处的采样点进行了局部曲线拟合．

在脉冲注入阶段，同时采集空闲两相响应电流峰值进行作差计算，读取并存储连续4次采样作差值，按采样顺序依次记为a0、a1、a2、a3．每次更新值时，采样计算的新值赋给a0，a0的旧值赋给a1，依次往下．当连续两次更新值都减小时，判断到达极值点．此时，对这4个数据进行拉格朗日拟合．由于采样间隔相等，可以简单地认为横坐标值为1到4的顺序数列，纵坐标为计算的差值，如表2所示．差值曲线拟合为

表2 曲线拟合的横纵坐标Tab.2 The abscissa and ordinate of curve fitting

f(x)=A1x3+A2x2+A3x+A4

(9)

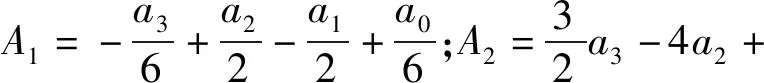
去除不在坐标范围内的解，得到曲线极大值点横坐标为xP，由此往前推得P点对应的时刻为

tP=t1-(4-xP)T

(10)

式中：t1为满足极值条件最后一次更新值的时刻，T为采样周期．其他极值点时刻tQ和tR计算相同．

由于3个绝对位置更新点等距分布，本文以多个相邻电周期的转速均值作为计算的转速：

(11)

式中：Δt1～Δtm为m组相邻位置更新点间的时间差值，即tP、tQ和tR间的顺序差值．

此外，由于最后一次更新值的实际转子位置已经越过了极大值点位置，在大转速时，利用极值点与最后一次更新值的横坐标距离，结合转速推算出最后更新值时的实际转子位置为

θ1=θP+ωn-1(4-xP)T

(12)

式中：ωn-1为前一时刻转速．其他时刻的位置计算公式为

θn=θn-1+360n/60fc

(13)

式中：fc为转子位置更新频率．

实际运行中发现电流传感器采样值有波动，两次相邻采样值会因为波动导致误判．为此，需对采样数据滤波，将此刻采样值与前一时刻采样值比较作差，差值大于波动范围，才决定此刻为有效采样．波动范围的确定是通过在同一位置处多次采样记录响应电流峰值，将采样值中出现的最大值与平均值或平均值与最小值作差，取两者中较大的值的两倍为波动范围．滤波后，采样值之间不再是等距的，需要记录采样次数作为横坐标，如表2所示．为简便计算，可以选择只拟合3个采样差值．此时，式(10)和式(12)需变为

tP=t1-(x0-xP)T

(14)

θ1=θP+ωn-1(x0-xP)T

(15)

3 仿真分析

为了验证理论分析的正确性，本文基于Simulink 对该方法进行了模型搭建和位置检测仿真．模型基于三相12/8结构的SRM，额定功率是4 kW．采用转速电流双闭环的PI控制，电流采用PWM斩波控制，母线电压为60 V．电机开通角为3°，关断角为16°，转速给定为600 r/min．

图4为电机稳定运行时的三相电流波形图，每相有导通时的斩波电流区间和两个脉冲注入区间．图5为转子实际位置θ1和计算位置θc比较图，其中0°代表A相不对齐位置，转子以45°为一个周期．图中转子位置在0°附近误差值很大，这是因为实际位置进入了下一个角度周期，而计算位置还在上一个周期，实际误差值Eθ仍然是很小的．图6为转子误差的放大图，可以看见，误差在0.3°左右．

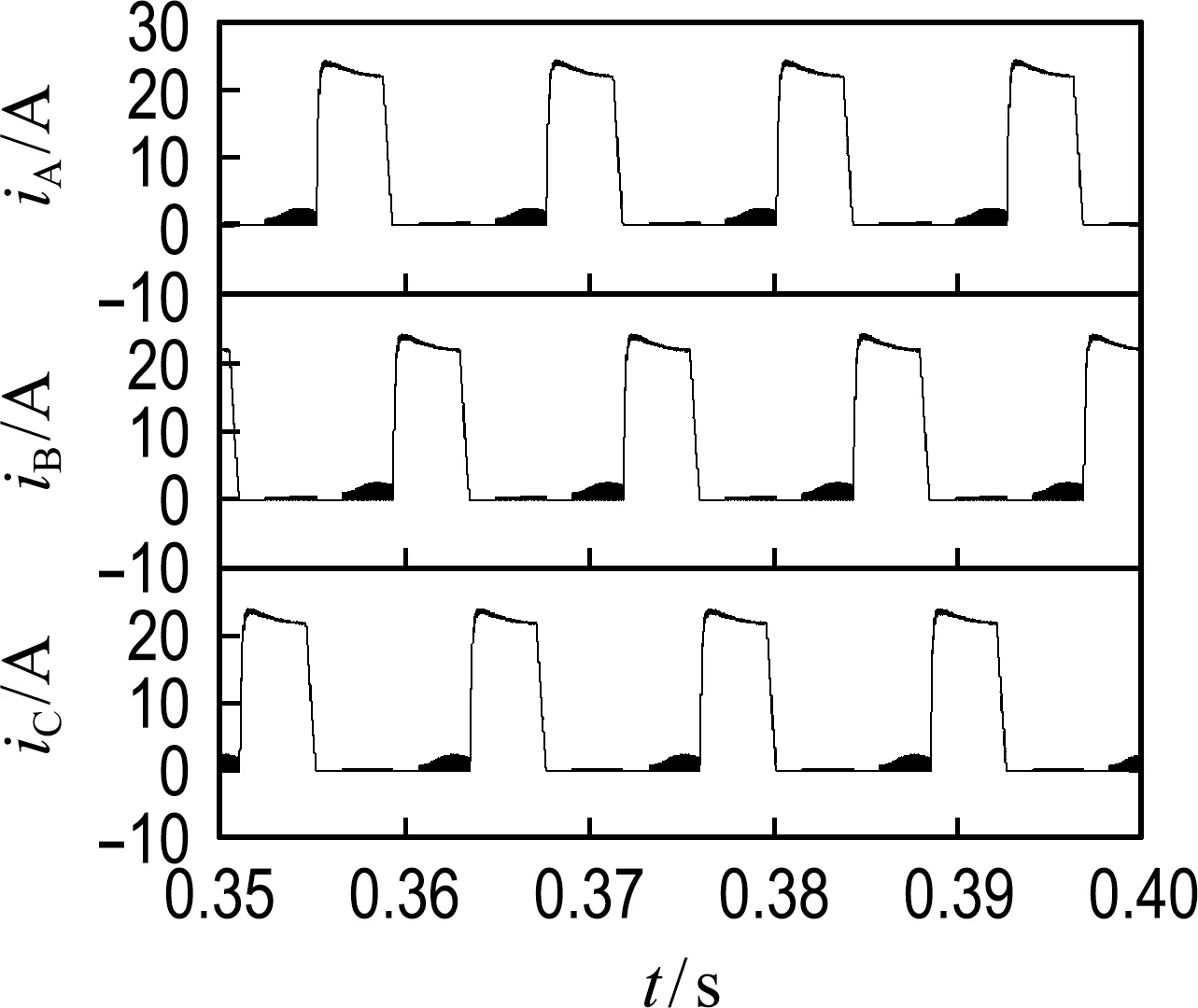
图4 三相电流波形图Fig.4 Three-phase current waveforms

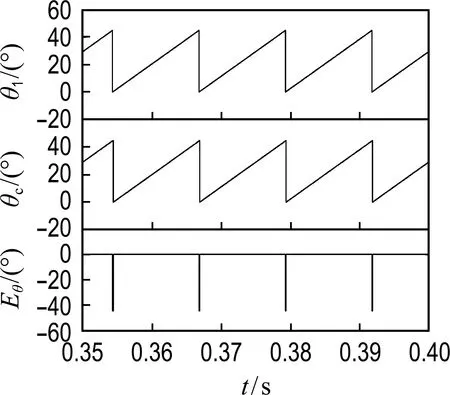
图5 实际转子位置和计算转子位置比较Fig.5 Comparison of actual rotor position and calculated rotor position

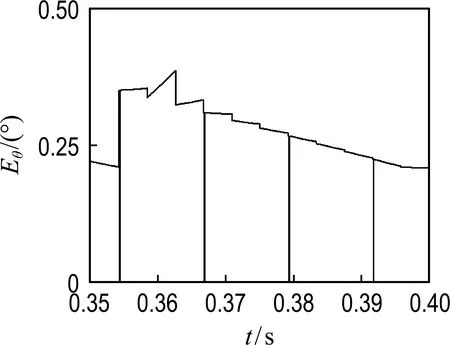
图6 位置误差放大图Fig.6 Enlarged image of position error

图7为实际和计算转速图，可以看出，计算转速与实际转速很契合，转速计算方法有效可行．位置检测的仿真模型说明本文方法位置检测精度较高，具有可行性．目前模型只进行了位置检测，无位置控制由实验部分验证．

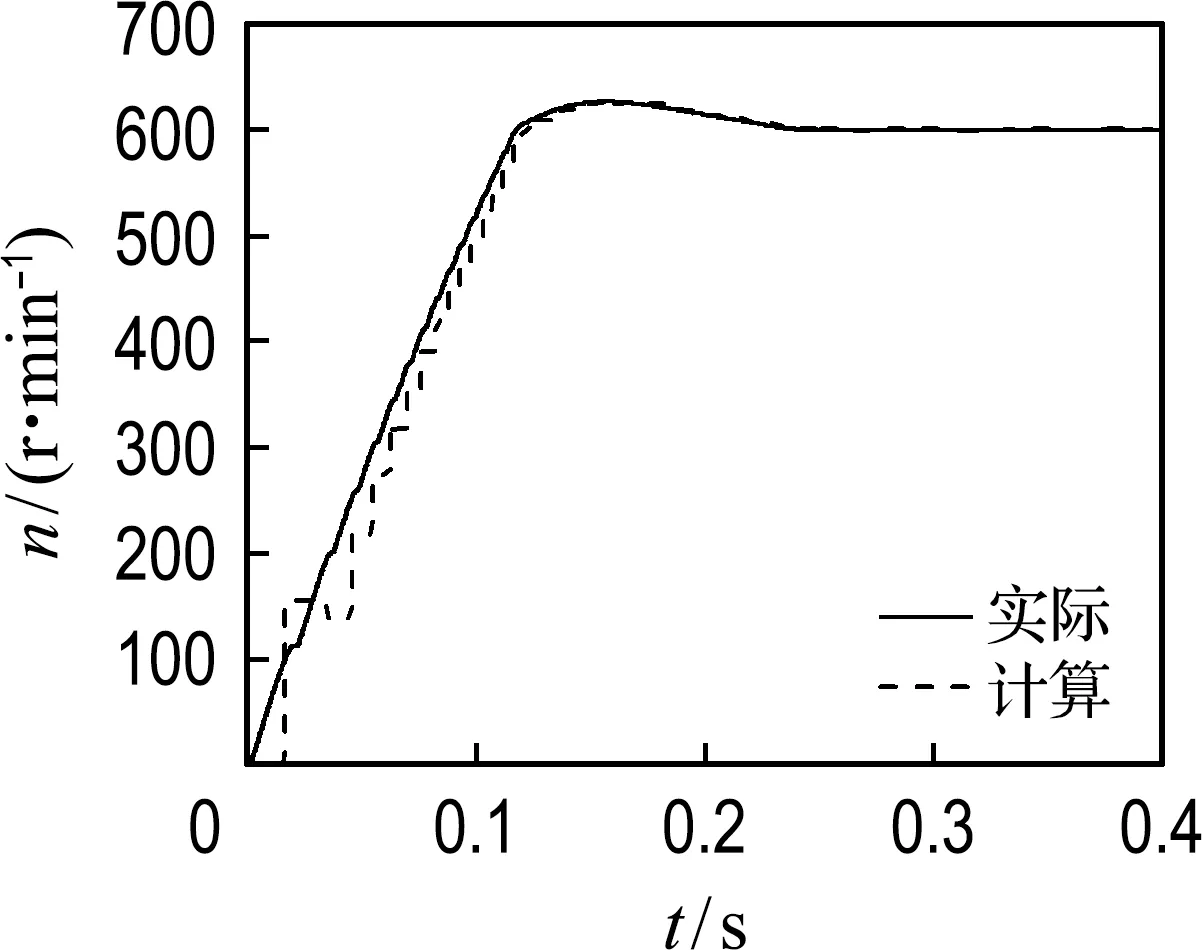
图7 实际转速和计算转速对比Fig.7 Comparison of actual rotary speed and calculated rotary speed

同时为了说明该方法具有良好的转矩特性，在仿真中与传统两相脉冲注入法进行了比较．传统两相脉冲注入法是利用电感的交点处作为特殊位置，每相的导通区间只有三分之一周期，以图1中的B相为例，导通区间为[22.5°，37.5°]．本文方法的导通区间则为R点所在转子位置开始，最大可到37.5°，有着更广的导通区间选择．图8为本文方法和传统两相脉冲注入法在电机转速稳定时的三相合成电磁转矩比较，转速稳定时导通区间都选为三分之一周期．由图可见本文方法的输出转矩波动更小，这是因为该方法是在每相不对齐位置处附近开始导通，电感变化小，急剧上升的电流仍产生较稳定的转矩，且关断位置处的续流电流仍产生正的转矩；而传统法在关断位置处的续流电流则产生负的转矩．图9反映了在同一PI参数控制下，本文方法有着更快的转速响应速率，因为该方法在起动低速时导通区间可以选为二分之一周期．

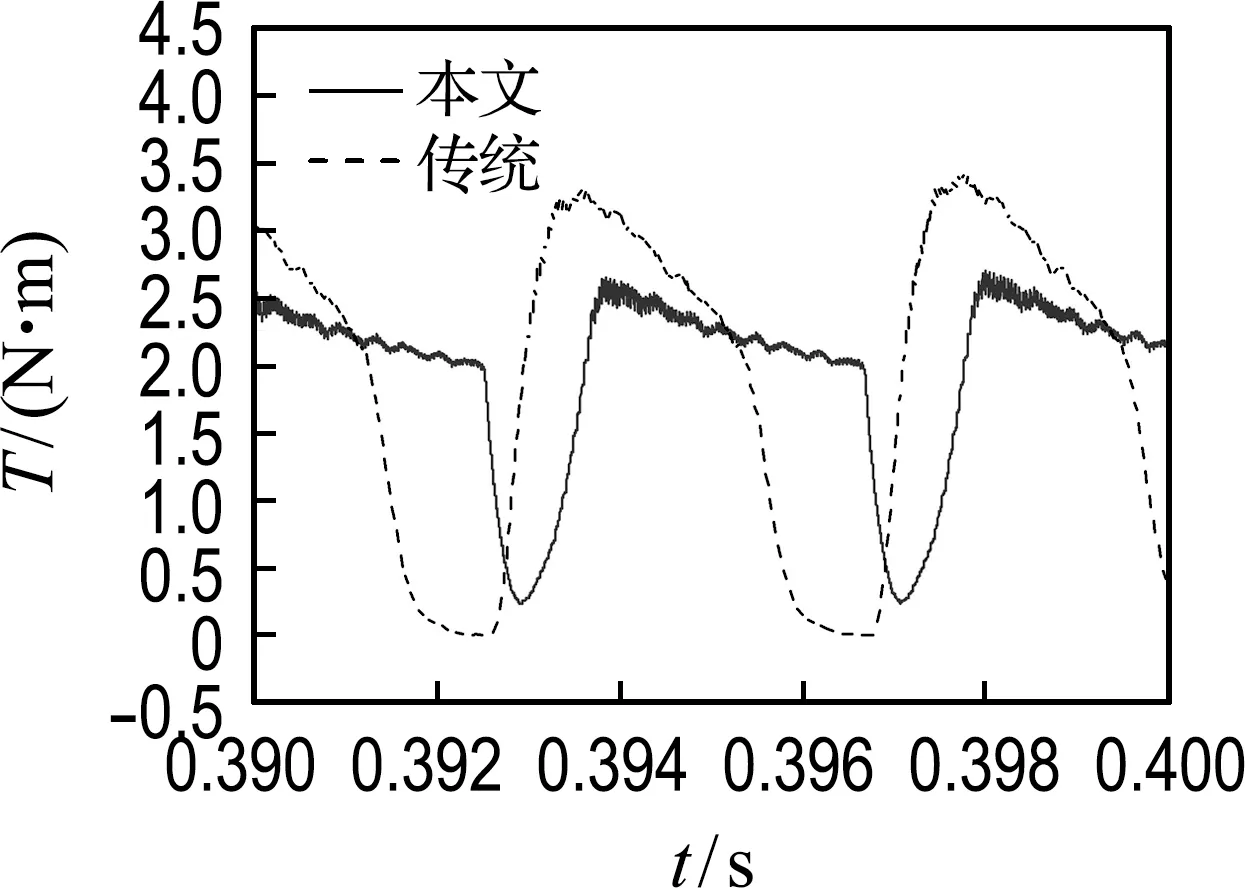
图8 本文方法和传统两相脉冲注入法600 r/min的电磁转矩Fig.8 The electromagnetic torque of the method in this paper and the traditional two-phase pulse injection method at 600 r/min

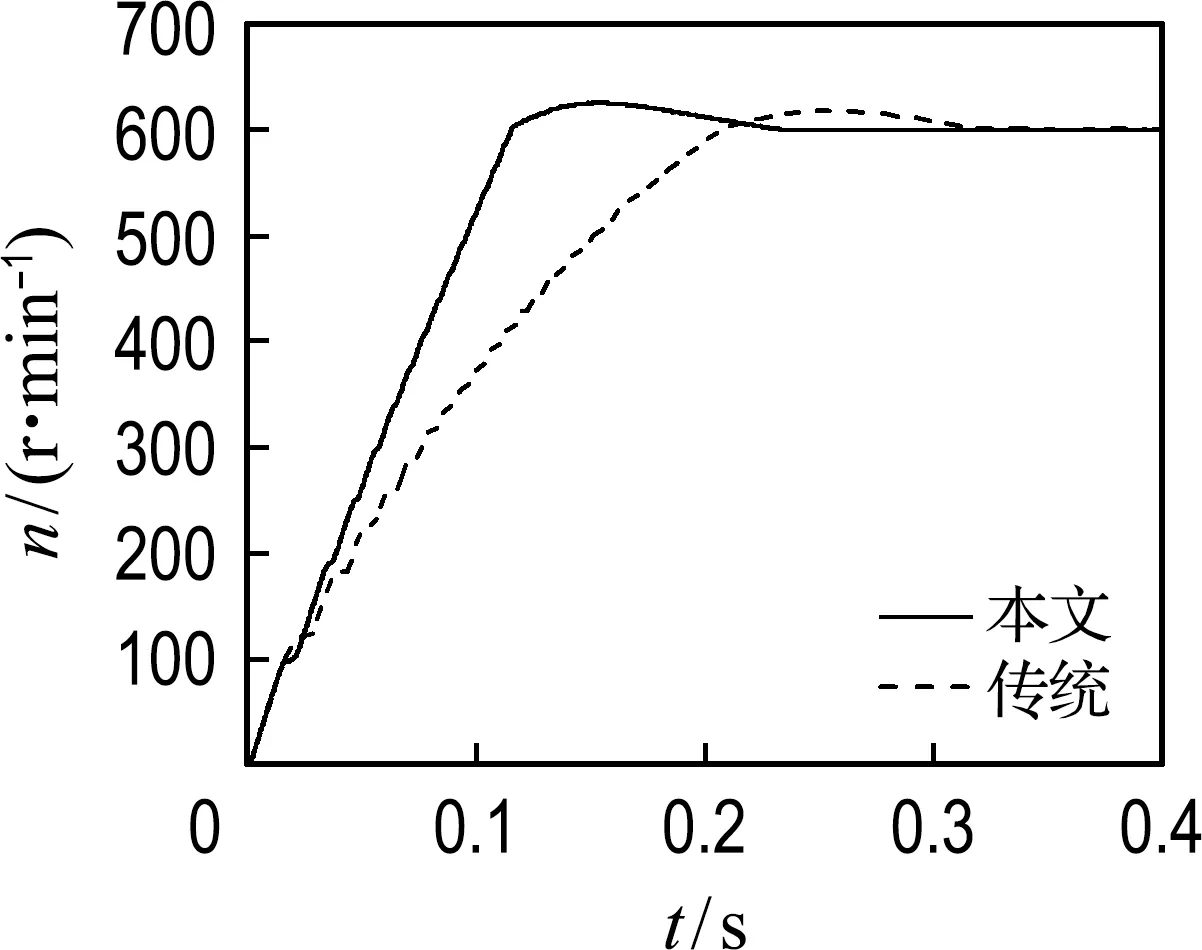
图9 本文方法和传统两相脉冲注入法的转速响应比较Fig.9 The response rotary speed comparison between the method in this paper and the traditional two-phase pulse injection method

4 实验验证

为了实现无位置传感器控制和进一步说明控制方法的可行性及特点，本文基于一台12/8结构的SRM进行了实验验证．实验中数字处理器采用TI公司的TMS320F28069芯片，功率电路使用三相不对称半桥结构，脉冲电流由电流传感器经过硬件放大电路后采样，保留了光电位置传感器，用于比较计算位置和实际位置．

首先不考虑旋转电动势，通过式(4)和(5)计算出极大值点的转子位置．当转速为900 r/min及以上时，考虑旋转电动势，通过式(8)来计算．

图10(a)和图10(b)分别为转速300 r/min和600 r/min的三相电流波形图，与仿真波形图相似，脉冲响应电流的峰值因转子位置而变化．图11 是控制过程中该方法计算的转速和位置传感器获得的转速比较，可见误差小，且能很好地响应转速变化．但在转速稳定时，图中脉冲注入计算的转速有着毛刺现象般的波动．这是由于响应电流采样值受到环境的干扰和曲线拟合的计算误差，造成了位置检测误差，使得计算的转速有所波动．

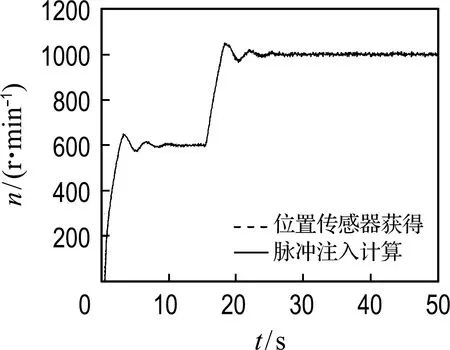
图11 脉冲注入计算转速和位置传感器获得转速比较Fig.11 Comparison of calculated rotary speed by pulse injection and actual rotary speed from position sensor

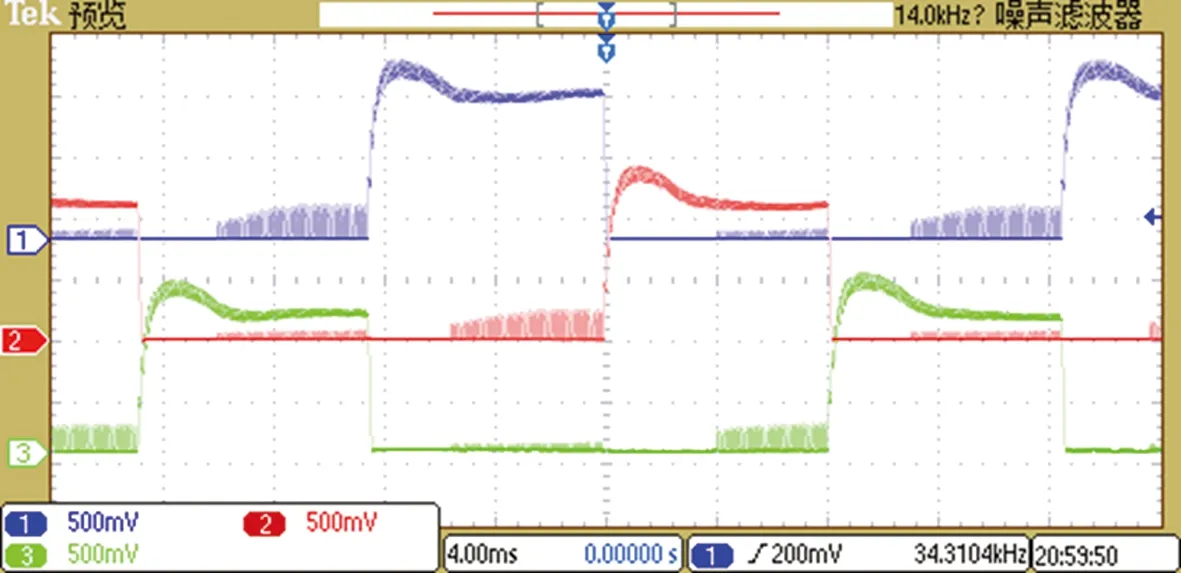
(a)300 r/min

在实验中，还实时记录了检测位置和实际位置，方便作对比．以位置传感器得到的位置作为实际位置，以两相响应电流峰值差法计算的位置作为检测位置，编写软件每隔0.1 ms同时将两种方式的位置信息存储在芯片中，实时导出数据，得出图12所示的不同转速下的位置比较和误差图．

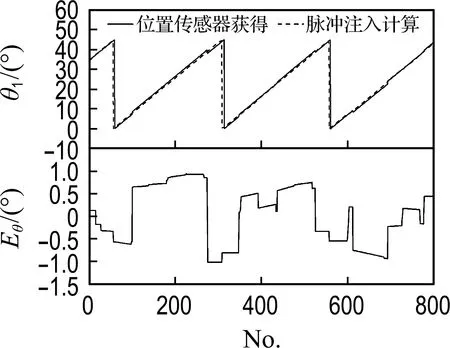
(a)300 r/min

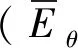
因此，在中低速时该方案得到的估算位置和实际位置间的误差不大，能很好地替代位置传感器，具有可行性．并且，在转速较大时能有很好的转矩输出，没有拖尾电流，符合运行要求．

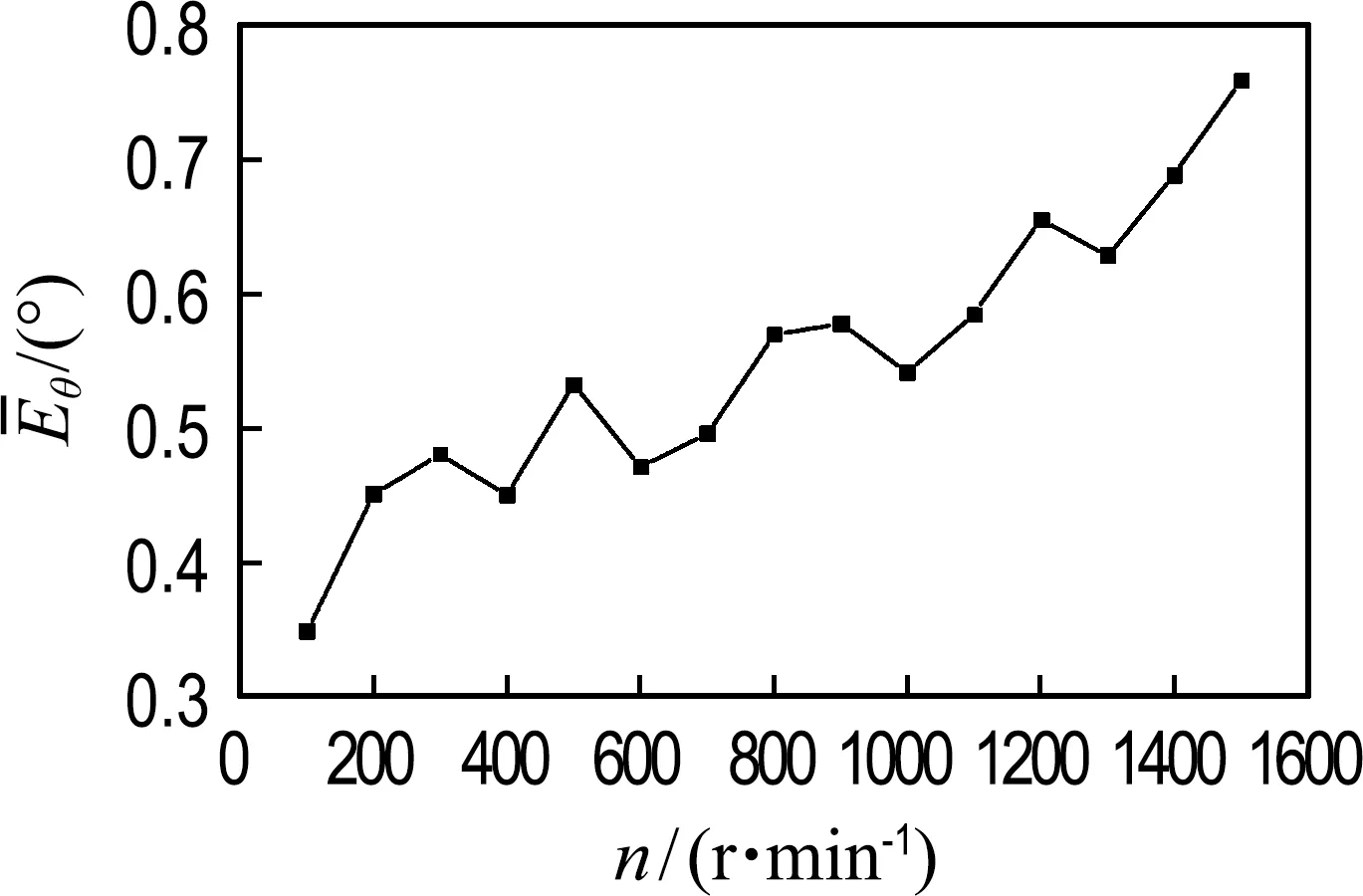
(a)检测位置平均误差

5 结 语

本文基于两相脉冲注入，研究了一种新型无位置传感器控制方法．利用两相响应电流峰值间的差值，通过其极大值点得到转子位置信息．该方法无须设定电流阈值，且在极大值点处换相有着更加宽广的导通区间，更符合电机运行的换相要求，对于不同转速，有着灵活的导通和关断角度选择．同时考虑了采样值间的离散程度，在极值点处对采样值进行拉格朗日曲线拟合，拟合计算虽然简单但有效．在实际运行时，针对电流采样值波动的问题，提出了滤波方法，该方法虽然减小了曲线拟合的精度，但能避免误判的发生，是至关重要的．由于本文控制方法是基于高频脉冲的注入，曲线拟合也有着精度限制，只能适用于中低速运行的情况．另外极大值点对应的转子位置虽然需要事先计算出来，但是在计算中可以考虑旋转电动势的影响．最后进行的仿真和实验结果证明了理论分析的可行性，具有一定的工程应用价值．