含参集值向量拟均衡问题和对偶问题解Lipschitz连续性

孟 旭 东

(南昌航空大学科技学院，江西 共青城 332020 )

0 引 言

集值向量拟均衡问题是变分不等式、优化问题、交通问题、不动点问题等的统一模型[1-2]．集值向量拟均衡问题解的稳定性分析是最优化理论和应用中的一个重要课题．稳定性蕴含了各类连续性，如半连续性[3-4]、连续性[5-6]、Hausdorff连续性[7-8]等．集值向量拟均衡问题解的稳定性成果不仅可以为集值向量拟均衡问题解的连通性、对偶性、近似计算研究奠定坚实的理论分析依据，而且广泛应用于数理经济、资源配置、交通网络、管理决策及工程设计等众多领域．

(参数)集值向量拟均衡问题解的Hölder连续性[9-11]和Lipschitz连续性[12-16]是近年来学者们研究的热点课题，对其研究的核心方法主要涉及标量化方法与非线性尺度化方法．借助标量化方法，Peng等在文献[9]中获得了一类参数集值映射弱广义Ky Fan不等式近似解映射的Hölder连续的充分性条件；Lam等在文献[10]中建立了参数向量均衡问题集值近似解映射的Hölder连续的充分性定理．运用非线性尺度化方法，Wangkeeree 等在文献[11]中得到了具集值映射参数广义向量拟均衡问题解映射的Hölder连续的最优性条件．结合标量化技术，Li等在文献[12]中借助Hausdorff度量的概念，建立了有关向量均衡问题近似解映射的Lipschitz连续性定理，并将其应用于最优化问题和参数变分不等式；Sadeqi等在文献[13]中研究了参数集值向量均衡问题近似解映射的Lipschitz连续性；Han在文献[14]中给出了参数广义向量均衡问题强有效近似解映射的Lipschitz连续的最优性条件；孟旭东等在文献[15]中分析了含参集值向量均衡问题近似解映射的Lipschitz连续性，并应用于含参集值向量优化问题近似解映射的Lipschitz连续的充分性条件；在文献[16]中借助向量函数的强凸(凹)性和单调性，应用分析方法建立了参数强向量原始与对偶均衡问题解映射Lipschitz连续的充分性定理；在文献[17]中获得了含参向量优化问题的弱解映射、解映射、弱最优值映射及最优值映射的上Lipschitz连续和下Lipschitz连续的充分性定理．万德龙等在文献[18]中于解映射不具任何凸性、单调性和单值性的条件下，给出了参数非凸弱广义Ky Fan不等式解映射Lipschitz连续的充分性条件． 本文在赋范线性空间中借助不同于以上文献的研究方法研究目标函数和约束函数在参数扰动下两类含参集值向量拟均衡问题和对偶问题解的Lipschitz连续性定理．

1 准备知识

设F：X×X×N→2Y{∅}，K：X×M→2X{∅} 为集值映射，对每个点(λ，μ)∈M×N，研究以下两类含参集值向量拟均衡问题，分别简记为问题(PSVQEP1)与问题(PSVQEP2)．

问题(PSVQEP1)：找到点x0∈K(x0，λ)，使得

F(x0，y，μ)∩(Y(-int(C)))≠∅，∀y∈K(x0，λ)

问题(PSVQEP2)：找到点x0∈K(x0，λ)，使得

F(x0，y，μ)⊂Y(-int(C))，∀y∈K(x0，λ)

记集合E(λ)={x∈X|x∈K(x，λ)}，用S1(λ，μ)与S2(λ，μ)分别表示问题(PSVQEP1)的解集与问题(PSVQEP2)的解集，即

S1(λ，μ)={x∈E(λ)|F(x，y，μ)∩

(Y(-int(C)))≠∅，∀y∈K(x，λ)}

与

S2(λ，μ)={x∈E(λ)|F(x，y，μ)⊂

Y(-int(C))，∀y∈K(x，λ)}

问题(PSVQEP1)与问题(PSVQEP2)的对偶问题分别记为问题(DPSVQEP1)与问题(DPSVQEP2)．

问题(DPSVQEP1)：找到点x0∈K(x0，λ)，使得

F(y，x0，μ)∩(-Y(-int(C)))≠∅，∀y∈K(x0，λ)

问题(DPSVQEP2)：找到点x0∈K(x0，λ)，使得

F(y，x0，μ)⊂-Y(-int(C))，∀y∈K(x0，λ)

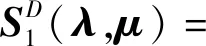
(-Y(-int(C)))≠∅，∀y∈K(x，λ)}

与

-Y(-int(C))，∀y∈K(x，λ)}

定义1[14]设L≥0，G：M→2X{∅}为集值映射，称G在M上为L-Lipschitz连续的当且仅当对任意的点λ1，λ2∈M，有

定义2设L≥0，F：X×X×N→2Y{∅}为集值映射，

(1)称F在X×X×N上关于第1个变量为L-Lipschitz连续的当且仅当对任意的点(y，μ)∈X×N及点x1，x2∈X，有

(2)称F在X×X×N上关于第2个变量为L-Lipschitz连续的当且仅当对任意的点(x，μ)∈X×N及点y1，y2∈X，有

(3)称F在X×X×N上关于第3个变量为L-Lipschitz连续的当且仅当对任意的点(x，y)∈X×X及点μ1，μ2∈N，有

定义3设α≥0，β≥0，K：X×M→2X{∅}为集值映射，称K在X×M上为α-β-Lipschitz一致连续的当且仅当对任意的点(x1，λ1)，(x2，λ2)∈X×M，有

2 问题(PSVQEP1)与问题(PSVQEP2)解的Lipschitz连续性

本章研究问题(PSVQEP1)与问题(PSVQEP2)解的Lipschitz连续性，为叙述的简洁性，特给出以下基本假设．

设F：X×X×N→2Y{∅}，K：X×M→2X{∅} 为集值映射，U(λ0)×V(μ0)⊂M×N为给定点(λ0，μ0)∈M×N的邻域，对任意的点λ∈U(λ0)，记集合E(λ)={x∈X|x∈K(x，λ)}．

(H1)对任意的点(λ，μ)∈U(λ0)×V(μ0)，有S1(λ，μ)⊂E(λ)为非空紧子集；

(H2)对任意的点(λ，μ)∈U(λ0)×V(μ0)，有S2(λ，μ)⊂E(λ)为非空紧子集；

(H3)集值映射K(·，·)在E(U(λ0))×U(λ0)⊂X×M上为L1-L2-Lipschitz一致连续的；

(H4)对任意的点(λ，μ)∈U(λ0)×V(μ0)及点y∈E(U(λ0))S1(λ，μ)，存在点x1∈S1(λ，μ)，有

(H5)对任意的点(λ，μ)∈U(λ0)×V(μ0)及点y∈E(U(λ0))S2(λ，μ)，存在点x2∈S2(λ，μ)，有

(H6)对任意的点(λ，μ)∈U(λ0)×V(μ0)及点x∈E(λ)，集值映射F(x，·，μ)关于第2个变量在K(E(U(λ0))，U(λ0))上为L3-Lipschitz连续的；

(H7)对任意的点λ∈U(λ0)及点x，y∈E(λ)，集值映射F(x，y，·)关于第3个变量在V(μ0)上为L4-Lipschitz连续的；

首先讨论问题(PSVQEP1)解的Lipschitz连续性．

定理1假若条件(H1)、(H3)、(H4)、(H6)、(H7)、(H8)成立，则对任意的点(λ，μ1)，(λ，μ2)∈U(λ0)×V(μ0)，有

(1)

证明显然地，若S1(λ，μ1)=S1(λ，μ2)，则式(1)成立．

假设S1(λ，μ1)≠S1(λ，μ2)，分以下两种情形讨论：

情形1若S1(λ，μ1)⊄S1(λ，μ2)且S1(λ，μ2)⊄S1(λ，μ1)，对任意的点x(λ，μ1)∈S1(λ，μ1)S1(λ，μ2)，据条件(H4)知，存在点x(λ，μ2)∈S1(λ，μ2)，有

(2)

据点x(λ，μ1)∈K(x(λ，μ1)，λ)，x(λ，μ2)∈K(x(λ，μ2)，λ)，结合条件(H3)知，存在点x1∈K(x(λ，μ2)，λ)，x2∈K(x(λ，μ1)，λ)，有

(3)

(4)

由x(λ，μ1)∈S1(λ，μ1)，x(λ，μ2)∈S1(λ，μ2)，知存在点y1∈F(x(λ，μ1)，x2，μ1)∩(Y(-int(C)))，y2∈F(x(λ，μ2)，x1，μ2)∩(Y(-int(C)))，结合式(2)，有

ρ(F(x(λ，μ2)，x(λ，μ1)，μ2)，F(x(λ，μ2)，x1，μ2))+

ρ(F(x(λ，μ1)，x2，μ1)，F(x(λ，μ1)，x(λ，μ2)，μ2))≤

ρ(F(x(λ，μ2)，x(λ，μ1)，μ2)，F(x(λ，μ2)，x1，μ2))+

ρ(F(x(λ，μ1)，x2，μ1)，F(x(λ，μ1)，x(λ，μ2)，μ1))+

ρ(F(x(λ，μ1)，x(λ，μ2)，μ1)，F(x(λ，μ1)，x(λ，μ2)，μ2))

再注意到条件(H6)、(H7)，并结合式(3)与式(4)，得

据条件(H8)，知

又注意到点x(λ，μ1)∈S1(λ，μ1)S1(λ，μ2)任意性，有

(5)

再结合d(·，·)的定义，知

(6)

类似可得

(7)

据式(6)与式(7)知，式(1)成立．

情形2若S1(λ，μ1)⊂S1(λ，μ2)或S1(λ，μ2)⊂S1(λ，μ1)，不失一般性，不妨假设S1(λ，μ1)⊂S1(λ，μ2)，据d(·，·)的定义，得

(8)

类似情形1同样的论证过程知式(7)成立．结合式(7)与式(8)知，式(1)成立．

定理2假若条件(H1)、(H3)、(H4)、(H6)、(H9)成立，则对任意的点(λ1，μ)，(λ2，μ)∈U(λ0)×V(μ0)，有

(9)

证明显然地，若S1(λ1，μ)=S1(λ2，μ)，则式(9)成立．

假设S1(λ1，μ)≠S1(λ2，μ)，分以下两种情形讨论：

情形1若S1(λ1，μ)⊄S1(λ2，μ)且S1(λ2，μ)⊄S1(λ1，μ)，对任意的点x(λ2，μ)∈S1(λ2，μ)S1(λ1，μ)，据条件(H4)知，存在点x(λ1，μ)∈S1(λ1，μ)，有

(10)

据点x(λ2，μ)∈K(x(λ2，μ)，λ2)，x(λ1，μ)∈K(x(λ1，μ)，λ1)，结合条件(H3)知，存在点x1∈K(x(λ2，μ)，λ1)，x2∈K(x(λ1，μ)，λ2)，有

(11)

(12)

(13)

(14)

ρ(F(x(λ1，μ)，x(λ2，μ)，μ)，F(x(λ1，μ)，x1，μ))+

ρ(F(x(λ2，μ)，x(λ1，μ)，μ)，F(x(λ2，μ)，x2，μ))+

再注意到条件(H6)，并结合式(11)～(14)，得

据条件(H9)，知

又注意到点x(λ2，μ)∈S1(λ2，μ)S1(λ1，μ)任意性，有

再结合d(·，·)的定义，知

(15)

类似可证

(16)

据式(15)与式(16)知，式(9)成立．

情形2若S1(λ1，μ)⊂S1(λ2，μ)或S1(λ2，μ)⊂S1(λ1，μ)，不失一般性，不妨假设S1(λ1，μ)⊂S1(λ2，μ)，据d(·，·)的定义，得

(17)

类似情形1的论证过程知式(15)成立．结合式(15)与式(17)知，式(9)成立．

定理3假若条件(H1)、(H3)、(H4)、(H6)、(H7)、(H8)、(H9)成立，则对任意的点(λ1，μ1)，(λ2，μ2)∈U(λ0)×V(μ0)，有

ρ(S1(λ1，μ1)，S1(λ2，μ2))≤

(18)

证明注意到ρ(S1(λ1，μ1)，S1(λ2，μ2))≤ρ(S1(λ1，μ1)，S1(λ1，μ2))+ρ(S1(λ1，μ2)，S1(λ2，μ2))，并结合式(1)与式(9)知，式(18)成立．

现给出例子说明定理3中结果的有效性．

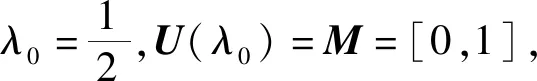
类似问题(PSVQEP1)解的Lipschitz连续性的论证过程，易得问题(PSVQEP2)解的Lipschitz连续性定理．

定理4假若条件(H2)、(H3)、(H5)、(H6)、(H7)、(H8)成立，则对任意的点(λ，μ1)，(λ，μ2)∈U(λ0)×V(μ0)，有

定理5假若条件(H2)、(H3)、(H5)、(H6)、(H9)成立，则对任意的点(λ1，μ)，(λ2，μ)∈U(λ0)×V(μ0)，有

定理6假若条件(H2)、(H3)、(H5)、(H6)、(H7)、(H8)、(H9)成立，则对任意的点(λ1，μ1)，(λ2，μ2)∈U(λ0)×V(μ0)，有

现举例检验定理6结论的有效性．

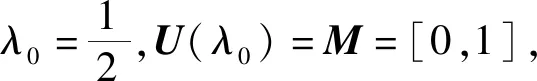
3 问题(DPSVQEP1)与问题(DPSVQEP2)解的Lipschitz连续性

本章分析问题(DPSVQEP1)与问题(DPSVQEP2)解的Lipschitz连续性，为叙述的方便性，特给出以下基本假设．

设F：X×X×N→2Y{∅}，K：X×M→2X{∅}为集值映射，U(λ0)×V(μ0)⊂M×N为给定点(λ0，μ0)∈M×N的邻域，对任意的点λ∈U(λ0)，记集合E(λ)={x∈X|x∈K(x，λ)}．

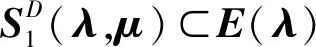
(T5)对任意的点(λ，μ)∈U(λ0)×V(μ0)及点x∈E(λ)，集值映射F(·，x，μ)关于第1个变量在K(E(U(λ0))，U(λ0))上为L5-Lipschitz连续的；

首先分析问题(DPSVQEP1)解的Lipschitz连续性．

定理7假若条件(T1)、(T3)、(H3)、(T5)、(T6)、(H7)成立，则对任意的点(λ，μ1)，(λ，μ2)∈U(λ0)×V(μ0)，有

(19)

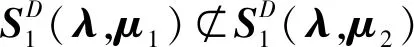
(20)

据点x(λ，μ1)∈K(x(λ，μ1)，λ)，x(λ，μ2)∈K(x(λ，μ2)，λ)，结合条件(H3)知，存在点x1∈K(x(λ，μ2)，λ)，x2∈K(x(λ，μ1)，λ)，有

(21)

(22)

ρ(F(x(λ，μ2)，x(λ，μ1)，μ2)，F(x2，x(λ，μ1)，μ1))+

ρ(F(x(λ，μ1)，x(λ，μ2)，μ2)，F(x1，x(λ，μ2)，μ2))≤

ρ(F(x(λ，μ2)，x(λ，μ1)，μ2)，F(x(λ，μ2)，

x(λ，μ1)，μ1))+ρ(F(x(λ，μ2)，x(λ，μ1)，μ1)，

F(x2，x(λ，μ1)，μ1))+ρ(F(x(λ，μ1)，x(λ，μ2)，μ2)，F(x1，x(λ，μ2)，μ2))

由条件(T5)、(H7)，式(21)、式(22)，得

并注意到(T6)，知

(23)

再结合d(·，·)的定义，知

(24)

类似可证

(25)

据式(24)与式(25)知，式(19)成立．

(26)

类似情形1的论证过程知式(25)成立．结合式(25)与式(26)知，式(19)成立．

定理8假若条件(T1)、(T3)、(H3)、(T5)、(T7)成立，则对任意的点(λ1，μ)，(λ2，μ)∈U(λ0)×V(μ0)，有

(27)

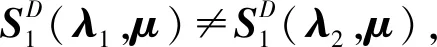
(28)

再据点x(λ2，μ)∈K(x(λ2，μ)，λ2)，x(λ1，μ)∈K(x(λ1，μ)，λ1)，并结合条件(H3)知，存在点x1∈K(x(λ2，μ)，λ1)，x2∈K(x(λ1，μ)，λ2)，有

(29)

(30)

(31)

(32)

ρ(F(x(λ1，μ)，x(λ2，μ)，μ)，F(x2，x(λ2，μ)，μ))+

ρ(F(x(λ2，μ)，x(λ1，μ)，μ)，F(x1，x(λ1，μ)，μ))+

再注意到条件(T5)，并结合式(29)～(32)，得

据条件(T7)，知

再结合d(·，·)的定义，知

(33)

类似可证

(34)

据式(33)与式(34)知，式(27)成立．

(35)

类似情形1的论证过程知式(33)成立．结合式(33)与式(35)知，式(27)成立．

定理9假若条件(T1)、(T3)、(H3)、(T5)、(T6)、(T7)、(H7)成立，则对任意的点(λ1，μ1)，(λ2，μ2)∈U(λ0)×V(μ0)，有

(36)

现给出例子检验定理9的结论．

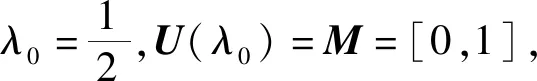
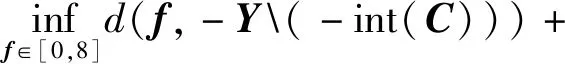
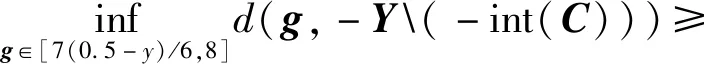
类似问题(DPSVQEP1)解的Lipschitz连续性的分析过程，易知问题(DPSVQEP2)解的Lipschitz 连续性定理．

定理10假若条件(T2)、(T4)、(H3)、(T5)、(T6)、(H7)成立，则对任意的点(λ，μ1)，(λ，μ2)∈U(λ0)×V(μ0)，有

定理11假若条件(T2)、(T4)、(H3)、(T5)、(T7)成立，则对任意的点(λ1，μ)，(λ2，μ)∈U(λ0)×V(μ0)，有

定理12假若条件(T2)、(T4)、(H3)、(T5)、(T6)、(T7)、(H7)成立，则对任意的点(λ1，μ1)，(λ2，μ2)∈U(λ0)×V(μ0)，有

现举例分析定理12结论的有效性．

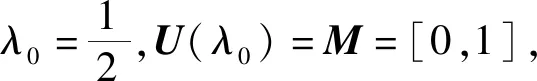
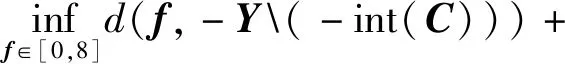
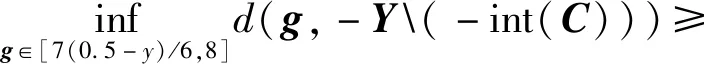
4 结 语

本文在目标函数和约束函数受参数扰动下于赋范线性空间中建立了含参集值向量拟均衡问题和对偶问题解的Lipschitz连续性定理．研究结果表明，两类含参集值向量拟均衡问题和对偶问题解的Lipschitz连续的充分性条件具有一致性数学结构，这为研究含参集值向量拟均衡问题和对偶问题(近似)解的Lipschitz连续性奠定了理论依据，并为获得广义含参集值向量拟均衡问题和对偶问题(近似)解的Lipschitz连续性和Hölder连续性统一框架模型提供了研究思路，同时为研究集值向量拟均衡问题解的连通性、对偶性、近似计算等提供了理论借鉴．