圈与圈克罗内克乘积图罗马{3}-控制

2022-05-23高红，黄佳欢，刘仁邦，杨元生

大连理工大学学报 2022年3期

高红，黄佳欢，刘仁邦，杨元生

(1.大连海事大学理学院，辽宁大连 116026；2.大连理工大学计算机科学与技术学院，辽宁大连 116024 )

0 引言

给定图G=(V，E)，V是图G的顶点集合，E是图G的边集合．集合N(v)={u|uv∈E}称为顶点v的开邻域．图G的顶点个数称为阶．顶点v的度dG(v)为N(v)中包含的顶点个数，最大/小度记为Δ(G)/δ(G)．

本文研究圈与圈克罗内克乘积图的罗马{3}-控制数，给出圈与圈克罗内克乘积图罗马{3}-控制数的上界和下界．通过构造可递推的罗马{3}-控制函数可以得到圈与圈克罗内克乘积图罗马{3}-控制数的上界．结合前人给出的一般图罗马{3}-控制数的下界，可以得到圈与圈克罗内克乘积图罗马{3}-控制数的下界．

1 圈与圈克罗内克乘积图Cn×Cm

圈Cn与圈Cm克罗内克乘积图Cn×Cm是一个有mn个顶点的四正则图，其顶点集合和边集合分别为V(Cn×Cm)={vi，j|0≤i≤n-1，0≤j≤m-1}，E(Cn×Cm)={ei，j|ei，j=(vi，jvi-1，j+1)，0≤i≤n-1，0≤j≤m-1}∪{e′i，j|e′i，j=(vi，jvi+1，j+1)，0≤i≤n-1，0≤j≤m-1}，其中下标i和j分别对n和m取模．图1(a)表示图C3×C6，图1(b)表示其上的一个罗马{3}-控制函数，图中的数字表示的是f(vi，j)．

设G=Cn×Cm，f为图G上的罗马{3}-控制函数，则f可表示为

例如：

表示C3×C6上的罗马{3}-控制函数，其图形如图1(b)所示．

(a)C3×C6

2 Cn×Cm罗马{3}-控制数的界

2.1 Cn×Cm罗马{3}-控制数的下界

若G=Cn×Cm，则图G的阶数为mn，最大度Δ(G)=4，由定理1可得下面的推论．

推论1若G=Cn×Cm，当m，n≥3时，则有γ{R3}(G)≥mn/2．

2.2 Cn×Cm罗马{3}-控制数的上界

定理2对于任意的正整数m≥3，G=C3×Cm的罗马{3}-控制数上界为

γ{R3}(C3×Cm)≤9m5;m≡0,1,2,3,4,7,8,9,13,14,19(mod20)9m5+1;m≡5,6,10,11,12,15,16,17,18(mod20)ìîíïïïïïï

证明首先定义一个C3×C20上的罗马{3}-控制函数g(vi，j)(0≤i≤2，0≤j≤19)，

函数g也可以表示为下面更直观的形式：

情况1当m≡0，1，7，14(mod 20)时，构造C3×Cm上的罗马{3}-控制函数为f(vi，j)=g(vi，j mod 20)，图2显示的是C3×C21上的f．

图2 C3×C21上的fFig.2 f on C3×C21

此时，f的权重为

w(f)=m20×36=9m5; m≡0(mod20)m-120×36+2=9m+15=9m5; m≡1(mod20)m-720×36+13=9m+25=9m5; m≡7(mod20)m-1420×36+26=9m+45=9m5; m≡14(mod20)ìîíïïïïïïïïïïïïïï

情况2当m≡2，3，4，5(mod 20)时，构造C3×Cm上的罗马{3}-控制函数f如下：

图3显示的是C3×C24上按照上式定义的罗马{3}-控制函数f．

图3 C3×C24上的fFig.3 f on C3×C24

此时，f的权重为

w(f)=m-220×36+4=9m+25=9m5;m≡2(mod20)m-320×36+6=9m+35=9m5;m≡3(mod20)m-420×36+8=9m+45=9m5;m≡4(mod20)m-520×36+10=9m+55=9m5+1;m≡5(mod20)ìîíïïïïïïïïïïïïïïïï

情况3当m≡8，9，10，15，19(mod 20)时，构造C3×Cm上的罗马{3}-控制函数f如下：

图4(a)显示的是C3×C10上按照上式定义的罗马{3}-控制函数f．

(a)C3×C10上的f

此时，f的权重为

w(f)=m-820×36+13+2=9m+35=9m5; m≡8(mod20)m-920×36+13+4=9m+45=9m5; m≡9(mod20)m-1020×36+13+6=9m+55=9m5+1; m≡10(mod20)m-1520×36+26+2=9m+55=9m5+1; m≡15(mod20)m-1920×36+33+2=9m+45=9m5; m≡19(mod20)ìîíïïïïïïïïïïïïïïïïïïïï

情况4当m≡6，12，13，16，17(mod 20)时，构造C3×Cm上的罗马{3}-控制函数f如下：

图4(b)显示的是C3×C16上按照上式定义的罗马{3}-控制函数f．此时，f的权重为

w(f)=m-620×36+9+3=9m+65=9m5+1; m≡6(mod20)m-1220×36+20+3=9m+75=9m5+1; m≡12(mod20)m-1320×36+21+3=9m+35=9m5; m≡13(mod20)m-1620×36+27+3=9m+65=9m5+1; m≡16(mod20)m-1720×36+27+5=9m+75=9m5+1; m≡17(mod20)ìîíïïïïïïïïïïïïïïïïïïïï

情况5当m≡11，18(mod 20)时，构造C3×Cm上的罗马{3}-控制函数f如下：

图5显示的是C3×C18上按照上式定义的罗马{3}-控制函数f．

图5 C3×C18上的fFig.5 f on C3×C18

此时，f的权重为

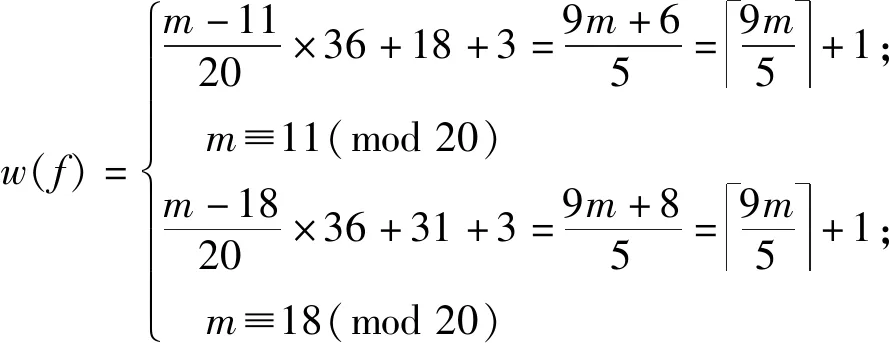
w(f)=m-1120×36+18+3=9m+65=9m5+1; m≡11(mod20)m-1820×36+31+3=9m+85=9m5+1; m≡18(mod20)ìîíïïïïïïïï

由情况1～5可知

γ{R3}(C3×Cm)≤w(f)=

9m5;m≡0,1,2,3,4,7,8,9,13,14,19(mod20)9m5+1;m≡5,6,10,11,12,15,16,17,18(mod20)ìîíïïïïïïïï

□

定理3对于任意的正整数m≥4，G=C4×Cm的罗马{3}-控制数上界为

γ{R3}(C4×Cm)≤13m5; m≡0,1,2,4(mod5),m≥513m5+1; m≡3(mod5)或m=4ìîíïïïïïïïï

证明

(a)C4×C4上的f

情况2当m≥5且m≠7时，先定义函数g(vi，j)(0≤i≤3，0≤j≤4)(如图7中前5列)：

然后，构造C4×Cm(m≡0，1，2，3，4(mod 5))上的罗马{3}-控制函数f如下：

图7显示的是C4×C17上按照上式定义的罗马{3}-控制函数f．

图7 C4×C17上的fFig.7 f on C4×C17

此时，f的权重为

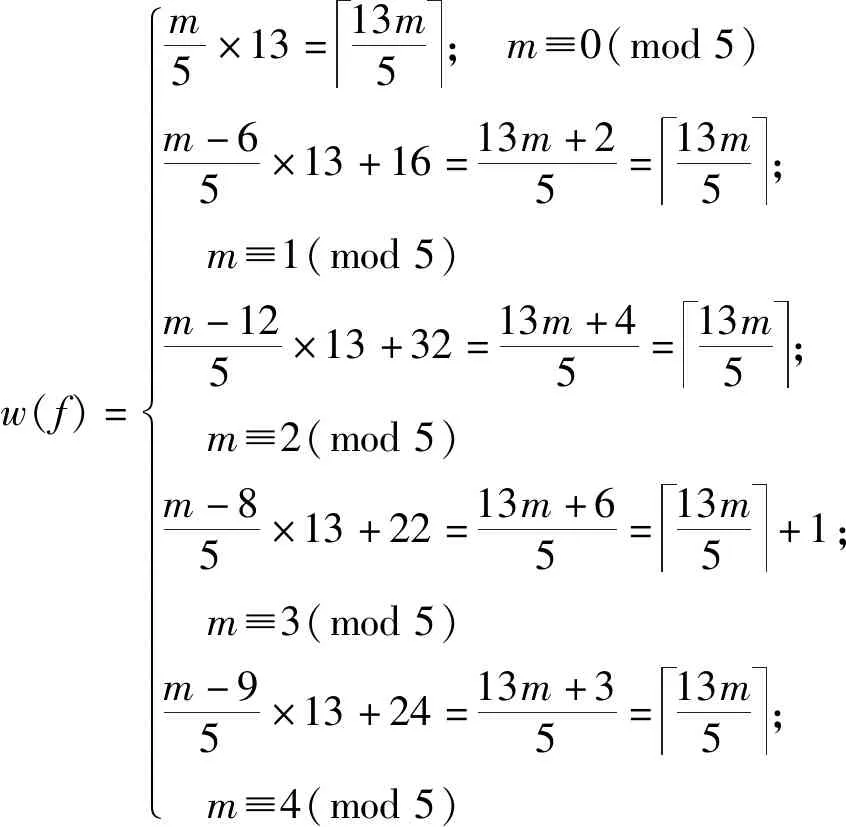
w(f)=m5×13=13m5; m≡0(mod5)m-65×13+16=13m+25=13m5; m≡1(mod5)m-125×13+32=13m+45=13m5; m≡2(mod5)m-85×13+22=13m+65=13m5+1; m≡3(mod5)m-95×13+24=13m+35=13m5; m≡4(mod5)ìîíïïïïïïïïïïïïïïïïïï

由情况1和2可知

γ{R3}(C4×Cm)≤w(f)=