基于等几何分析的离散变量拓扑优化方法研究
2022-05-23胡清元,李小渔,梁缘
胡 清 元, 李 小 渔, 梁 缘
(1.江南大学 理学院,江苏 无锡 214122;2.大连理工大学 运载工程与力学学部,辽宁 大连 116024 )
0 引 言
结构拓扑优化旨在根据给定的约束条件,寻求最优的材料分布,发挥材料最高性价比[1].基于传统有限元分析的拓扑优化方法发展成熟,涌现出了众多的优秀方法,例如基于单元惩罚密度的SIMP方法[2-3]、基于演化结构的ESO方法[4]、基于双向渐进结构优化的BESO方法[5]、基于水平集的level-set优化方法[6-7],以及基于显示边界描述的MMC/MMV方法[8-9]等.这些方法仍在不断发展,也被用于指导实际工程问题[10],取得了不同程度的成效.
然而,就目前广泛被采用的基于有限元SIMP方法的拓扑优化来说,仍存在两个亟待解决的问题.首先,受限于传统有限元单元的以直代曲特性,拓扑优化所得结果边界往往不够光滑,需要网格足够细密或经可视化后处理才能得到光滑边界;其次,SIMP方法通常会产生灰度单元,导致该处材料布局结果模糊.这些问题导致优化结果难以指导后续设计加工.
等几何分析于2005年被Hughes等提出[11],该方法直接采用CAD模型中天然内含的曲边单元进行有限元分析,将设计和分析融为一体.得益于等几何分析的优势,Gao等[12]采用密度分布函数定义结构拓扑,以得到光滑性和连续性可控的优化结果;董振宇[13]基于Catmull-Clark体细分方法,开展了多分辨率等几何拓扑优化的一系列研究;杨佳明等[14]采用混合B样条进行材料密度分布和等几何分析,研究了实体模型的等几何优化.
本文基于等几何分析,采用离散变量拓扑优化方法,针对平面问题展开理论算法研究.基于序列近似整数规划和正则松弛算法的离散变量拓扑优化算法由Liang等[15]提出,该方法将单元密度严格限制为0或1,因此可以得到完全黑白的材料布局.将离散变量拓扑优化方法引入等几何分析框架,一方面可以利用等几何分析曲边单元的优势,另一方面可以优化出清晰的结构边界,使得优化结果对后续设计加工更具指导性.
1 等几何分析简介
等几何分析采用非均匀有理B样条(NURBS)作为基函数同时插值几何和位移场,其本质可理解为采用NURBS作为形函数的等参有限元.因此,本章重点介绍NURBS及由此带来的等几何分析特性.
从一维单变量B样条函数出发,B样条函数可由预先给定的节点矢量Ξ生成:
Ξ=(ξ1ξ2…ξn+p+1)
(1)
节点下标i=1,2,…,n+p+1,最后一个下标编号给出了所生成的B样条函数的个数n和阶次p.接下来,利用Cox-de Boor递推公式
(2)
生成B样条函数Ni,p,如图1(a)所示.
由于B样条函数无法描述圆锥曲线,故对基函数进行有理化处理,给定权重wi,即可得到NURBS函数:
(3)
当权重都为1时,NURBS函数退化为B样条函数.搭配相应控制点pi,可生成曲线
(4)
通常,CAD和等几何分析所采用的节点矢量以0开始、以1结束,并要求所生成的NURBS函数是开的,即对于p次NURBS函数节点矢量Ξ,其开始的0和结束的1被重复p+1次.图1(b)给出了生成圆弧曲线的示例.
生成二维曲面需要扩充维度,为此,给定另一组节点矢量Ψ和权重,得到NURBS函数Rj,q(η),其中η为该维度的方向参数,j为函数个数,q表示函数阶次.搭配相应控制点pi,j,得到张量积曲面
(5)
与几何模型的插值类似,等几何分析采用相同的NURBS基函数近似位移场:
(6)
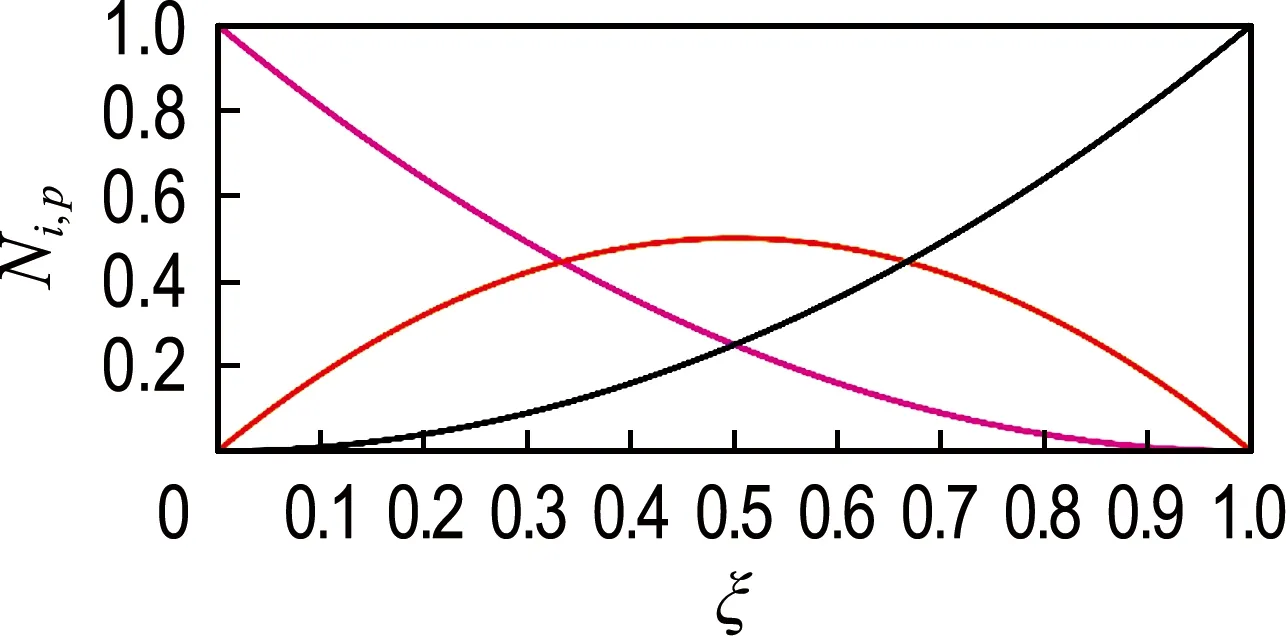
(a)NURBS基函数
其中ui,j=(ui,jvi,j),为对应控制点pi,j上的自由度,ui,j和vi,j分别表示该点沿x轴和y轴的位移.
等几何分析后续步骤与等参有限元相同.需要注意的是,与传统的等参有限元相比,等几何分析直接采用原始的几何模型进行分析,无须划分网格,也不产生离散误差.但实际上等几何分析仍然依赖网格,该网格在几何建模的过程中由节点矢量Ξ×Ψ自然地生成.
2 离散变量拓扑优化方法
考虑在给定材料用量的约束条件下,求结构最小柔顺性的问题.将结构离散为M个单元,令ρ为单元密度,问题的优化列式为
(7)
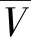
为求得目标函数c(ρ)的最小值,需要求出c关于ρi的变化率,即目标函数灵敏度.借鉴SIMP方法,假设单元弹性模量与单元密度之间的关系为
E=E0ρP
(8)
其中P=3是惩罚参数.目标函数的灵敏度为
(9)
根据Liang等[15]的方法,将式(7)转化为求解如下的整数线性规划问题:
(10)
由于整数线性规划的约束条件以及目标函数的组合复杂性,很难获得全局最优解.通过转化整数松弛变量约束以及引入拉格朗日乘子λ和σ,得到如下的对偶关系:
(11)
同时有
(12)
以及
(13)
这里β=2×104,是摄动参数.给定λ初始值,通过求解式(13)得到对偶变量σi,结合对偶关系式(11)得到原设计变量ρi,如果更新后的设计变量ρi满足收敛准则,即认为达到了近似解,跳出迭代;否则通过式(12)更新λ,继续迭代.
3 算法实现细节
本研究所述算法的代码实现基于开源等几何分析框架IGAFEM[16]和离散变量拓扑优化开源代码DVTOPCRA[17].在将两者有机融合的基础上,需要注意以下细节:
首先,需要注意的是,Liang等提出的离散变量优化算法[15]是基于密度的.考虑到如果将等几何分析的控制点密度作为设计变量,那么即使单个控制点的密度是非黑即白的,通过NURBS函数插值后所得曲线意义也将变得不明确,所涉及单元可能仍是灰度的.因此,本研究将单元密度作为设计变量.在参数空间Ξ×Ψ得到0或1的密度后,通过式(5)映射到物理空间,即得到包含曲边单元的材料布局,如图2所示.
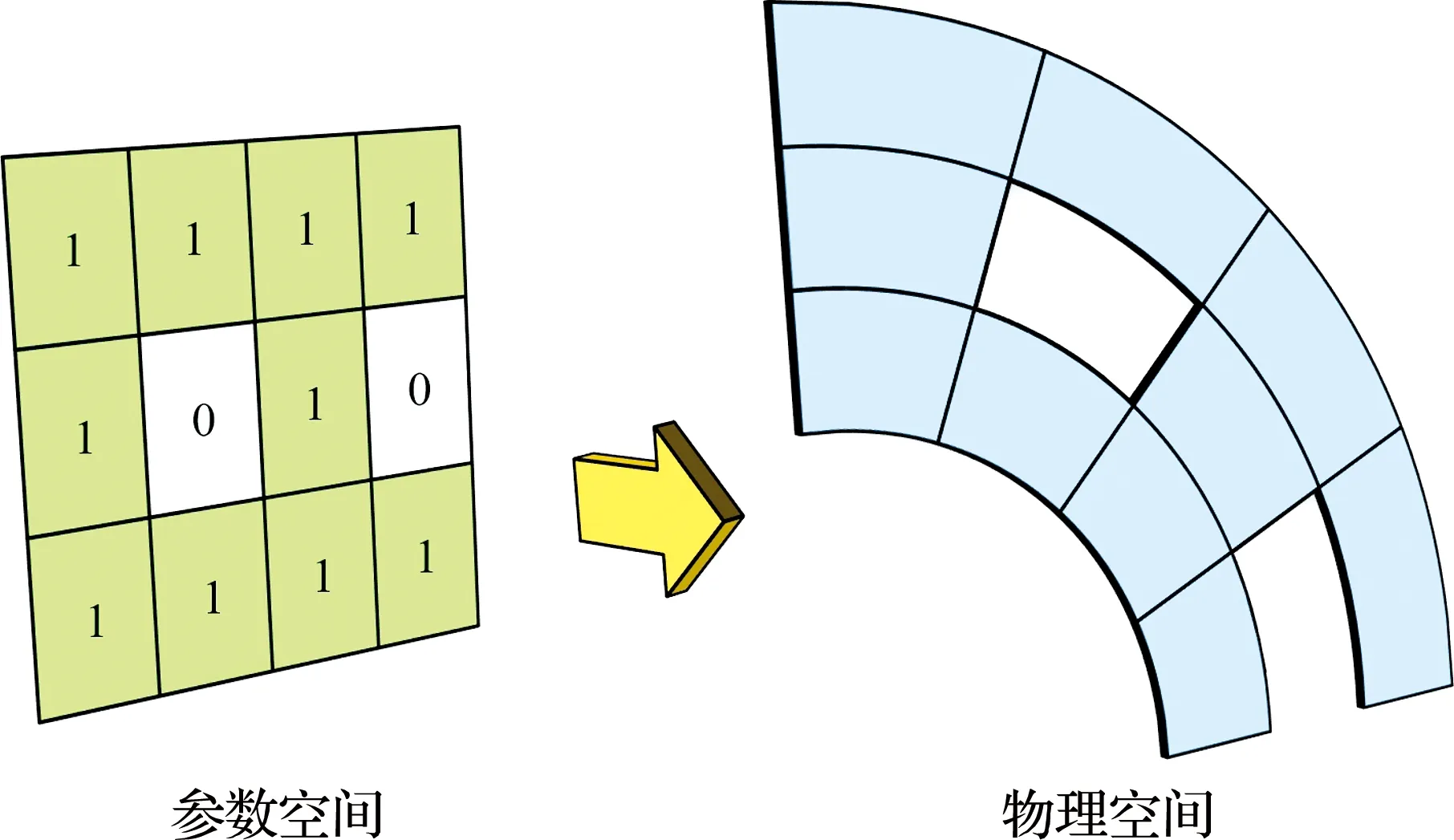
图2 参数空间单元映射到物理空间曲边单元Fig.2 Mapping from elements in parameter space to curved elements in physical space
此外,为避免出现棋盘格现象,需对灵敏度进行过滤.传统有限元中的灵敏度过滤方法高度依赖结构化网格,需要对邻近单元进行搜索.由于等几何分析中存在曲边单元,本文采用基于Helmhöltz 方程的隐式过滤方法[18],该方法无须搜索邻近单元,易于处理复杂网格.过滤公式为
(14)
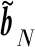
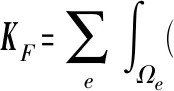
(15)
为标量问题的等几何刚度阵,Re为基函数插值矩阵,∇Re为基函数梯度矩阵,
(16)
(17)
最终得到过滤后的单元灵敏度列阵
(18)
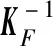
由于优化算法求解的是近似的子问题,需要严格控制迭代过程,保证近似子问题的解缓慢收敛到真实解.这里采用体分比缩减因子χ,用于逐渐减少材料用量约束,在当前体分比约束下计算收敛后,再按χ缩减体分比约束继续计算.根据数值测试,参数χ取值范围为[0.95,1.00).本文令体分比缩减因子χ=0.98,即假定每一轮迭代结构中只有2%的材料发生改变,以限制设计变量的变化范围,起到运动极限的作用,从而保证基于灵敏度的整数规划子问题(10)的近似精度.在未来工作中可以使用Liang等提出的基于信赖域的方法精确施加运动极限[19].
4 数值算例
4.1 悬臂梁
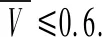

图3 悬臂梁Fig.3 Cantilever beam
本文方法所得优化结果见图4,迭代过程中的结构柔顺性变化和体分比v变化见图5.目标函数值为3 210 N·m.图6展示了优化后结构的应力分布,可见应力分布均匀,整体处于较低水平.

图4 悬臂梁优化结果Fig.4 Optimization result of the cantilever beam
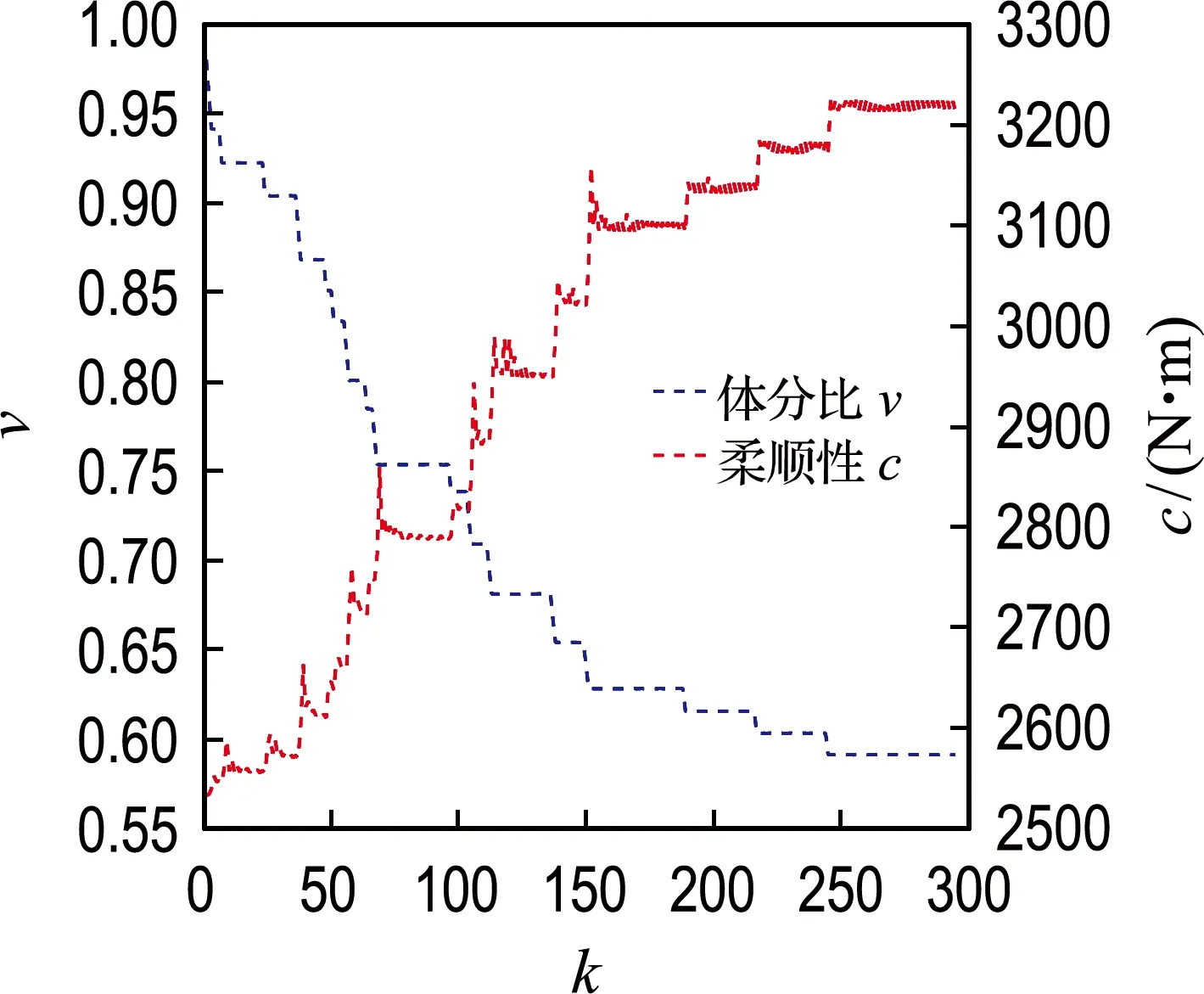
图5 悬臂梁迭代数据Fig.5 Iteration data of the cantilever beam

图6 悬臂梁应力分布Fig.6 Stress distribution of the cantilever beam
为了验证本文算法的有效性,在ABAQUS中采用了细密的有限元网格,图7中展示了ABAQUS的优化结果,目标函数值为3 394 N·m.由于连续体结构拓扑优化依赖于网格划分,而ABAQUS采用的有限元网格更加细密,因此本文方法所得结果与ABAQUS所得结果在构形上有所不同.离散变量下拓扑优化问题的数学本质是偏微分方程约束的非线性整数规划,因此不同的离散方法也会得到不同的局部最优解.图4与图7两种构形的目标函数值相近,则一定程度上可以说明两种优化结果构形的受力特性相似.

图7 悬臂梁ABAQUS优化结果Fig.7 Optimization result of the cantilever beam by ABAQUS
采用基于传统有限元的SIMP方法计算,网格划分与本文方法(图4)相同,优化结果见图8.可见SIMP方法优化结果边界产生大量灰度单元,边界模糊,而本文方法(图4)边界清晰,体现了本文方法的优势.

图8 悬臂梁SIMP法优化结果Fig.8 Optimization result of the cantilever beam by SIMP method
4.2 四分之一圆环
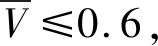
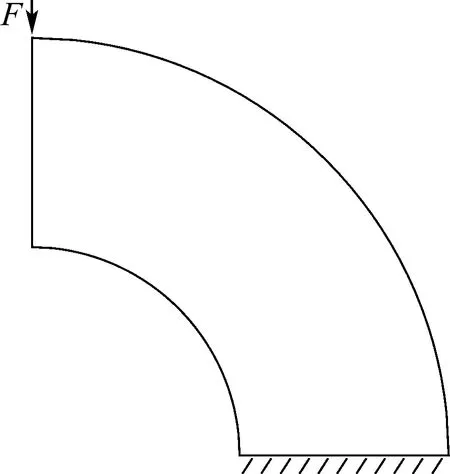
图9 四分之一圆环Fig.9 One-quarter annulus
采用本文方法得到的优化结果见图10,目标函数和材料用量迭代曲线见图11,目标函数值为28.6 N·m.应力分布图12表明,优化后的构形应力分布较为平均.图13为ABAQUS的优化结果,目标函数值为30.5 N·m.本文方法所得优化结果与ABAQUS结果相似,两种构形目标函数相近,验证了方法的有效性.

图10 四分之一圆环优化结果Fig.10 Optimization result of the one-quarter annulus
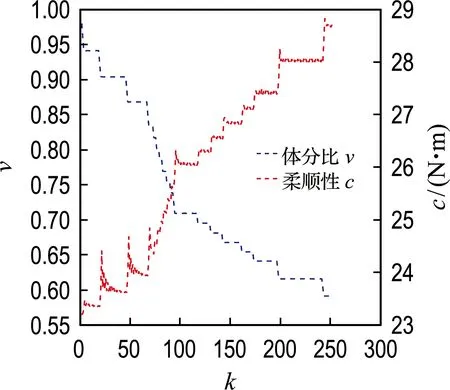
图11 四分之一圆环迭代数据Fig.11 Iteration data of the one-quarter annulus
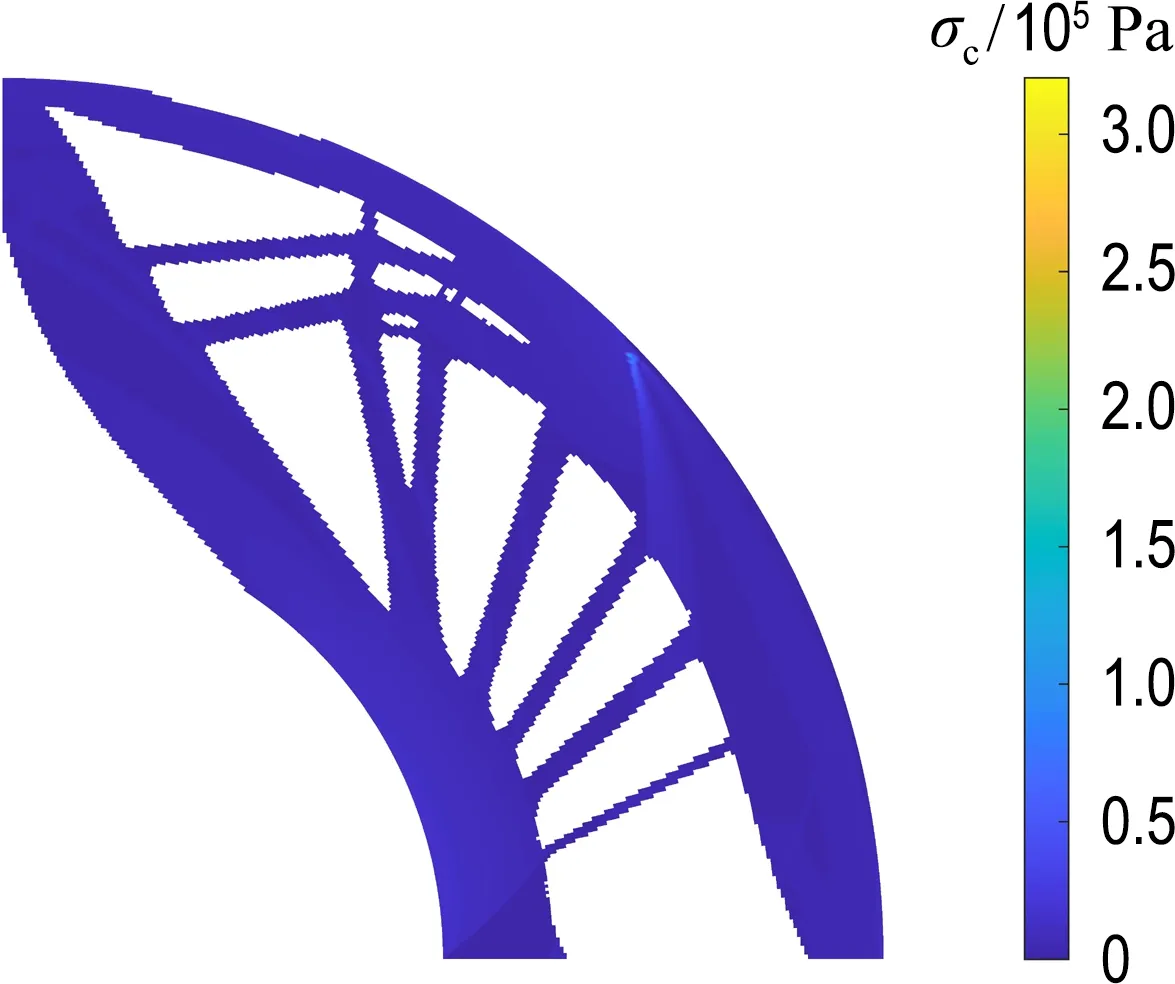
图12 四分之一圆环应力分布Fig.12 Stress distribution of the one-quarter annulus

图13 四分之一圆环ABAQUS优化结果Fig.13 Optimization result of the one-quarter annulus by ABAQUS
此外,ABAQUS分析所用自由度数为1.9×105,本文所用自由度数为6.7×104,相比ABAQUS节省了计算量.但本文所得到的结果中存在大量曲边单元,例如,将图10中画框部分放大为图14(a),可见在本文方法的优化结果中,对局部某些包含曲线边界的区域,采用较少单元即可使结构边界清晰、光滑;而ABAQUS单元对应部分(图14(b))虽然单元更密,但几乎所有曲线边界均呈锯齿状,通常需要采用黑线描边的方式进行可视化后处理.

(a)本文
5 结 语
针对基于传统有限元SIMP拓扑优化方法存在的问题,本文在等几何分析框架内,结合离散变量拓扑优化算法展开了研究.本文提出的优化方法结合了等几何分析和离散变量拓扑优化的优势,一方面允许曲边单元存在,另一方面单元密度为非黑即白的,因此优化结果在局部某些曲线边界上清晰光滑.本研究还采用了基于Helmhöltz方程的隐式过滤方法,节省了搜索邻近单元的计算量,对曲边单元过滤效果良好.
通过算例对比,验证了方法的有效性,展示了方法的优势.与传统有限元相比,本文方法优化计算所得的构形在整体上更加清晰、在局部上更加光滑,对后续设计和加工更具指导意义.
