基于二值化处理的纹波电机位置修正算法
2022-05-23彭邦煌钟益林刘梓曼
彭邦煌, 钟益林, 熊 斌, 刘梓曼, 方 旭
(比亚迪汽车工程研究院, 广东 深圳 518118)
纹波防夹是一种基于直流有刷电机电流波动间接获取电机位置的方法, 属于无传感器探测技术。 普通有刷电机通过适当结构上调整即可输出良好品质的纹波电流信号,因此基于纹波电流的位置测算具有良好应用前景。 相比于传统的霍尔防夹控制 (图1a), 使用如图1b所示的电机纹波电流实现防夹技术, 能够减少传感器和相关线束的使用,从而实现低成本与轻量化。
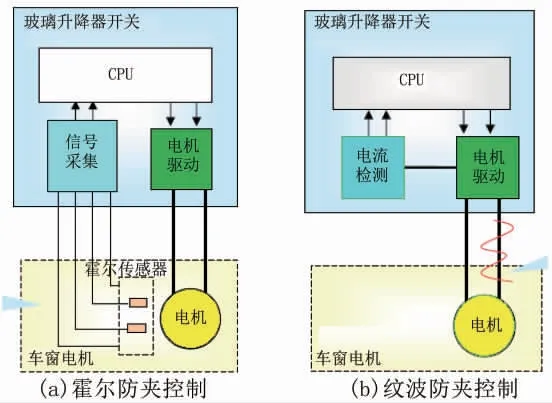
图1 霍尔防夹控制与纹波防夹控制电路图
1 纹波防夹概述
1.1 系统组成及应用
纹波防夹系统控制框图如图2所示, CPU驱动电机回路中串联纹波采集电阻, 实现纹波的差分信号采集。 电机防夹纹波信号采集示意见图3。

图2 纹波防夹系统控制框图

图3 电机防夹纹波信号采集示意图
1.2 纹波电机定位原理
直流有刷电机内部结构原理如图4 所示,其由1对对称布置的碳刷及8个电枢构成。 相邻两个电枢之间沟槽的存在, 使得电机在旋转过程中, 碳刷与换向器之间的电阻也在变化,由此产生的电流波动称为纹波电流。 通过采集电流, 解析其中纹波的个数, 可以确定电机当前的位置。

图4 纹波产生电机结构原理
2 纹波电机位置建模
利用纹波电流方法进行位置判断建立数学模型。 如图5所示, 以变量p表示车窗的当前位置, 表征车窗相对于下止点的距离, 零点为车窗下止点。 由于电机每转一圈, 纹波电流输出固定数量的纹波, p随纹波数改变, 当车窗上升时, p增大; 当车窗下降时, p减小。

图5 防夹区示意图
由下止点不间断运行到上止点产生的纹波数代表车窗最大行程, 用H示, 同一窗的H通常要求保持不变, 在车窗初始化自学习后保存在软件中。 通过比较p与H的差值判定车窗是否位于防夹区。 车窗上沿密封条还有一定深度且此区域不防夹, 在判定防夹区时, 将封条区产生的纹波数扣除。
利用纹波电流输出的纹波信号, 获取每个纹波的周期T, 电机转速越快, 纹波周期越短, 转速越慢, 纹波周期越长。 车窗在上升过程中遇到堵转时, 纹波周期增大, 设置合适的上限阈值T, 当纹波周期T大于T时, 可以认为车窗在上升过程中发生了堵转, 若堵转发生在防夹区 (图6),则判断车窗发生了夹持, 车窗下降一定行程保护夹持物安全。 同时记录在夹持过程中以及夹持后下降过程的位置信息p, 用于后续车窗升降使用。

图6 防夹触发条件
为了保证车窗的可靠到顶, 确保严密关窗, 当车窗位置高于防夹区域并且电机发送堵转维持一定时间时, 判断车窗到顶, 之后令车窗停止。
上述控制都基于电机纹波信号的采集处理, 电机纹波信号工况有: ①启动工况, 电流瞬间拉高, 随着转子加速至恒定转速, 电流进入稳定阶段; ②稳定工况, 恒流运行阶段, 电流波动较小, 电流大小由载荷决定; ③停止工况,电流迅速增大, 电机堵转后电流维持在一定值, 若维持堵转状态, 电机产生大量热; ④软停工况, 用户在玻璃升降器运行中突然操作开关进行停止, 且可能来回调整运作;⑤防夹工况, 触发防夹策略, 玻璃升降器进行保护操作并停止。
上述停止、 软停和防夹工况电机都会断电, 断电后电机的纹波信号不能有效提供。 但由于机械惯性, 电机还会运行一段行程, 此行程随着系统运行的累加, 超出系统判定公差, 导致防夹功能丧失。
电机断电后, 运行位置理论上可以采用系统控制预测,采用此种方式同时带来的工程控制问题如图7所示, 需要控制玻璃升降系统状态一致性等问题, 且不可预测。 本文针对此类问题, 提出了可行的解决方案。

图7 预测纹波信号工程控制
3 纹波电流信号采集处理
3.1 硬件采集方案
3.1.1 纹波电流信号硬件采集
利用电机断电后自感作用物理特性, 采集电机自感纹波信号, 补齐电机运行全过程信号, 纹波信号全过程采集见图8。
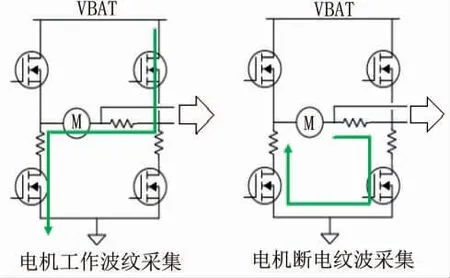
图8 纹波信号全过程采集
按图8改制电机 (带霍尔传感器) 及电路控制, 采集信号如图9所示, 电机断电后由于机械惯性, 产生了纹波信号, 此信号与电机正常运作平衡位置波动的波形不同, 是复合波。
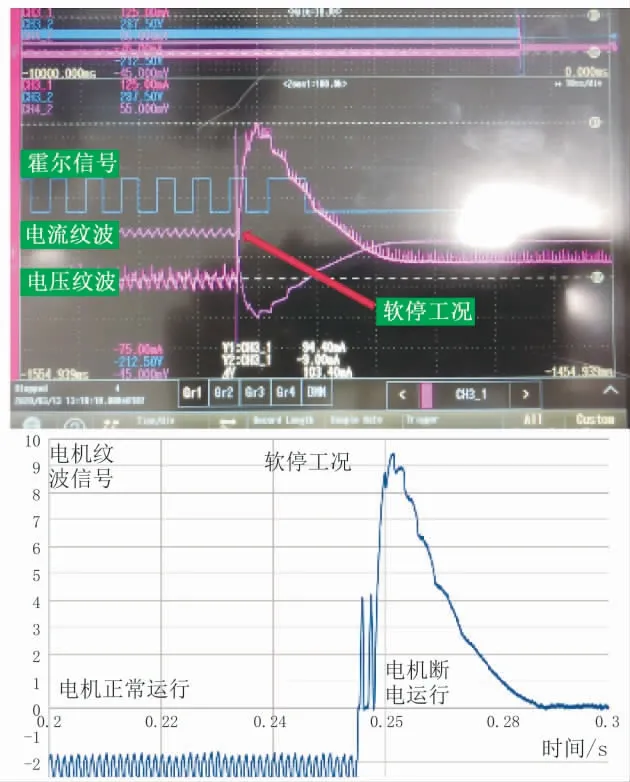
图9 电机断电后纹波信号采集
针对复合波形, 从系统控制物理特性进行分析研究如下。

式中: Q——系统状态切换储藏能量; u(t)——系统能量转换电压效应, 与Q理想等效为线性关系, 比例因子k;R——系统的等效电阻。
通过模型计算, 电机断电后复合波为系统切换后冲击波、 纹波与指数衰减波的复合调制波, 见图10。

图10 电机断电后复合波的成分
冲击波与指数衰减波是系统状态切换的系统携带初能导致, 为系统的物理特性, 无法从根本上抑制, 为得到单一可处理的纹波, 对复合波形进行解调。
3.1.2 波形特性分析
冲击波函数关系见式 (2), 波形特性见图11。

图11 冲击波时域、 频域特性
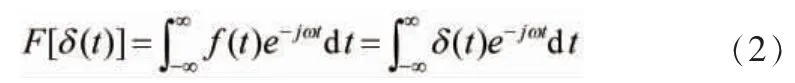
指数波函数关系如式(3)~(5)所示, 波形特性如图12所示。


图12 单边指数波时域、 频域特性
电机纹波函数关系见式 (6), 波形特性如图13所示。

图13 电机纹波时域、 频域特性
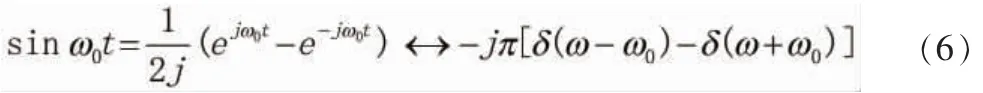
通过波形特性分析, 带通滤波可以解调所需的电机纹波信号。
3.1.3 纹波信号带通滤波调制
设计巴特沃思滤波带通滤波器(图14), 技术指标 如下。
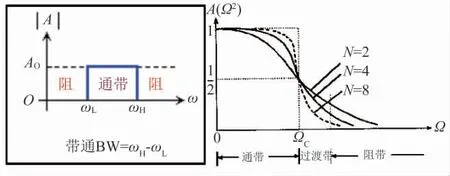
图14 带通滤波器
带通: 2×π×400~2×π×800; 带阻: <2×π×50&>2×π×1150。
设计的硬件电路见图15, 测试的滤波效果见图16, 可以有效过滤采集电机断电后产生的5个纹波。

图15 带通滤波电路
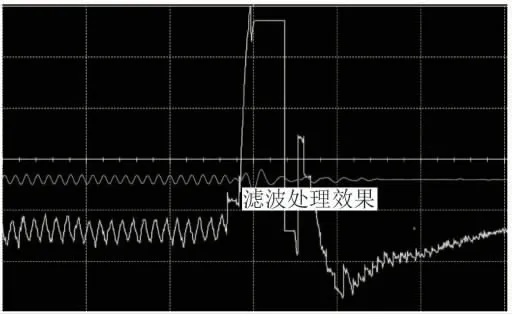
图16 带通滤波测试效果
3.1.4 纹波信号硬件采集设计难点
采用无源电路滤波设计产生的电感、 电容规格参数很大, 电路设计不易集成且成本大。 采用有源电路滤波可以克服元器件参数问题, 但由于系统设计工况的互斥: 电机堵转工况工作频率很低(150Hz左右), 需要低通采集保留; 电机软停工况产生指数冲击波,需要带通过滤, 过滤100Hz以 下 波 形; 导 致电路设计滤波器阶数很高, 成本高不易实现 ,具体如图17~图18所示。

图17 二阶有源带通滤波器(BPF)

图18 互斥滤波要求
基于上述设计需求, 且电路滤波方案实现困难, 本文采用数字滤波处理。
3.2 软件采集处理
3.2.1 数字滤波器
数字滤波器, 是指输入、 输出均为数字信号, 通过一定运算关系改变输入信号所含频率成分相对比例或者滤除某些频率成分器件。
1) 从功能上分: 低通、 带通、 高通、 带阻。
2) 从实现方法上分: 有限冲激响应FIR、 无限冲激响应IIR。
3) 从 设 计 方 法 上 来 分: Chebyshev (切 比 雪 夫),Butterworth (巴特沃斯) ……
本文采用了切比雪夫Ⅰ型低通滤波器, 切比雪夫Ⅰ型带通滤波器。 数字滤波器滤波系统函数及运算线性差分方程如下。

3.2.2 数字信号采样
从模拟滤波器变换所得数字滤波器单位取样响应h(n)是相应模拟滤波器单位脉冲响应h(t)等间隔取样值, 即

如图19所示, T为取样周期, 为避免采样频率与信号频率 (1.5kHz)混叠问题, 采样频率设计采用10kHz。

图19 信号数字采样
3.2.3 切比雪夫Ⅰ型低通滤波器设计
电机启动、 稳态、 堵转工况纹波信号处理设计低通切比雪夫Ⅰ型滤波器, 技术指标如下。 Ω: 0~2π×1500, a衰减幅值小于1dB; 高阻Ω: >2π×2000, a减幅值大于15dB;滤波器指标如图20所示, 模拟参数设计函数如下。

图20 低通滤波器性能指标

式中: Ω——有效通带截止频率; ε——与通带波纹有关的参量, 0<ε<1; V(x)——N阶切比雪夫多项式, 定义为

求得响应模拟系统函数如下。

对模拟系统函数进行频率去归一化处理, 再双线性变换, 将整个s平面映射到整个z平面上, 映射关系如下。

滤波器设计参数如图21所示, 为4阶低通滤波, 考虑CPU运算, 系数值a、 a、 a、 a、 a、 b、 b、 b、 b可圆整调节。
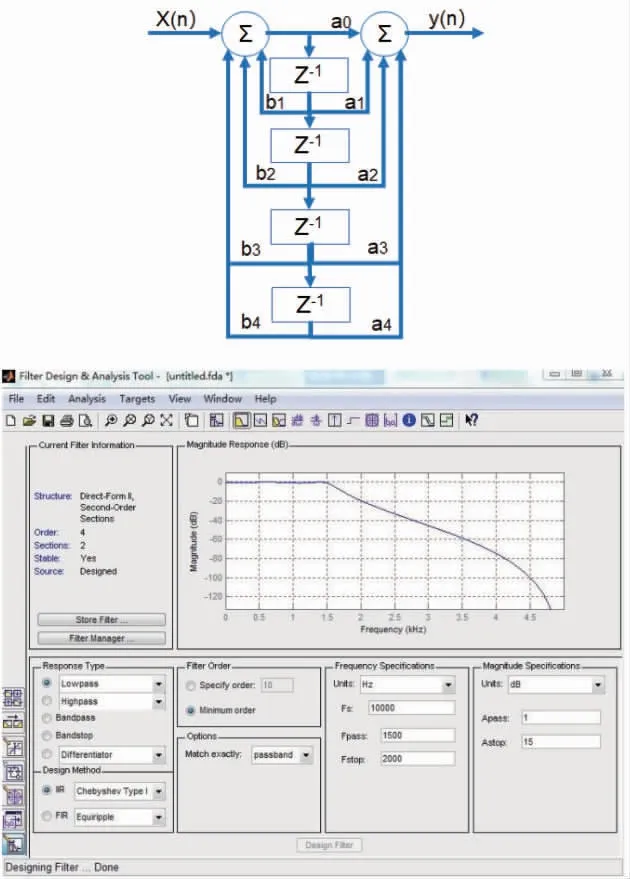
图21 4阶低通滤波器设计参数
3.2.4 切比雪夫Ⅰ型带通滤波器设计
设计带通切比雪夫Ⅰ型滤波器, 技术指标如下。 Ω:2π×300~2π×1000, a衰减幅值小于1dB; 带阻Ω: <2π×100且>2π×1500, a衰减幅值大于15dB。
对上文的模拟系统函数进行频率去归一化处理 (同上), 通过式(14)~(15)进行低通转带通函数处理, 再双线性变换 (同上) 将整个s平面映射到整个z平面上。
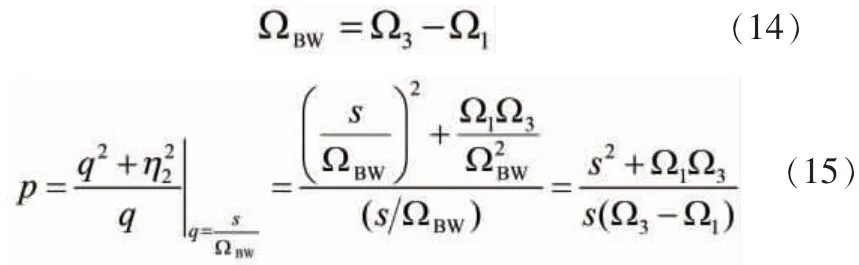
式中: Ω, Ω——分别是通带下限和上限截止频率;Ω, Ω——分别是阻带的下限、 上限频率。
滤波器设计参数如图22所示, 为6阶带通滤波, 考虑CPU运算, 系数值a、 a、 a、 a、 b、 b、 b、 b、 b、 b可圆整调节。

图22 6阶带通滤波器设计参数
3.2.5 滤波器测试
对设计滤波器分别进行常温25℃、 高温85℃和低温-30℃测试, 效果如图23~图25所示, 数字滤波器有效过滤采集了电机纹波信号。 其中在堵转控制过程频繁吸合, 产生很多杂波, 需要优化控制, 且低温软停过程, 由于阻力因素,电机行程运动很小。
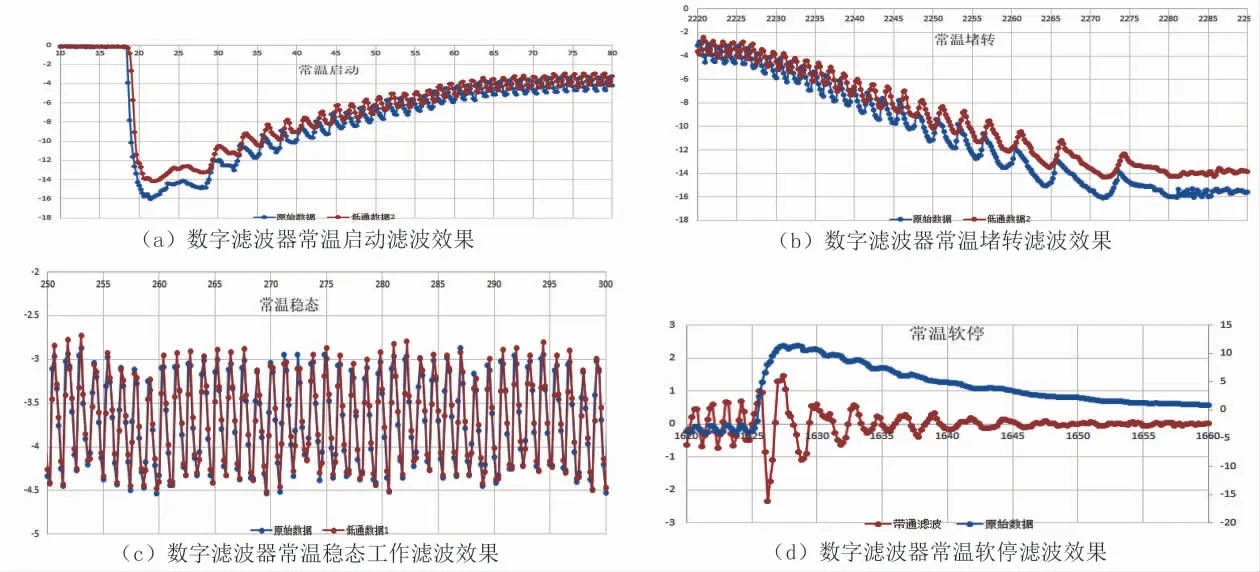
图23 滤波器常温25℃测试效果

图25 滤波器低温-30℃测试效果
3.3 纹波的计算
3.3.1 二值化处理
对滤波处理结束后纹波信号, 最终需要转化为电机转动位置, 所以需要对波形进行计数, 本文采用二值化处理,如图26所示。

图26 数字滤波器纹波二值化处理
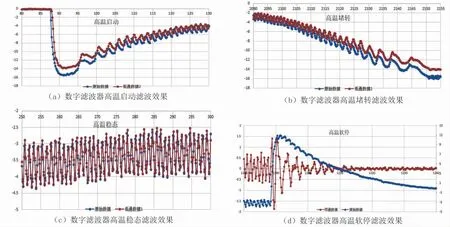
图24 滤波器高温85℃测试效果
车窗电机不同工作工况, 纹波信号存在差异, 采用单一数字二值化控制处理控制模型, 存在丢波问题。 针对不同的工况, 分别设计了4种二值化处理控制模型。
3.3.1.1 电机稳态工作工况
通过电机稳态工作典型波形分析 (图27), 设计二值化处理控制模型1。 单边波幅采集点N=6、 波幅≌1, 数字二值化控制处理采用N=6的递推平均滤波法判幅, 幅值A采用近似半波功率A(根据波形匹配取值0.6) 判波处理。

图27 数字低通滤波信号波形分析
数字二值化控制处理控制模型1:
A=Y(N)-Y(N-6)
A≥A取值1
A<A取值0
控制处理后二值化波形如图28所示。

图28 数字低通滤波信号二值化
车窗电机不同工作温度二值化处理如图29所示 。 在低温、 常温与高温工况下, 对相应工况下的波形能有效地实行二值化, 准确实现纹波的计数, 不存在丢波或多波的现象。

图29 车窗电机不同工作温度稳态二值化处理
3.3.1.2 电机启动工况
启动工况纹波信号波形周期大, 采用单一数字二值化控制处理控制模型, 存在丢波问题 (图30), 通过图31的波形分析, 设计二值化处理控制模型2。
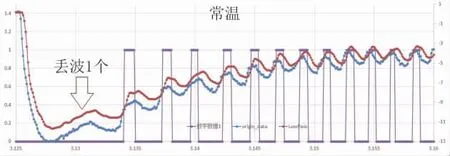
图30 单一数字二值化控制处理丢波问题
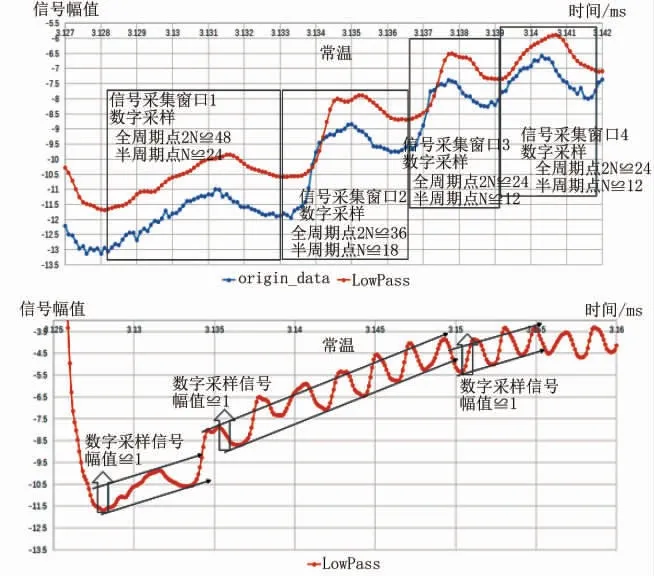
图31 启动纹波信号波形分析
数字二值化控制处理控制模型2 (N=12, A=0.24):
A=Y(N)-Y(N-12)
A≥A取值1.5
A<A取值0
控制处理后二值化波形如图32所示, 启动阶段丢失的波形被修正。

图32 启动纹波信号波形修正
车窗电机不同工作温度二值化处理如图33所示。 二值化处理控制模型2分别在相应的温度下弥补了启动工况大周期波形丢波的现象。

图33 车窗电机不同工作温度启动二值化处理
3.3.1.3 电机中途断电工况
车窗电机中途运行停止断电, 电机工作产生纹波信号物理特性存在差异。 通过波形特性分析, 波形衰减快, 波幅值小, 设计二值化处理控制模型3。
数字二值化控制处理控制模型3 (N=6, A=0.3):
A=Y(N)-Y(N-6)
A≥A取值1.5
A<A取值0
控制处理后二值化波形如图34所示, 电机中途停止后的小幅值波形被识别, 对纹波数进行了修正。
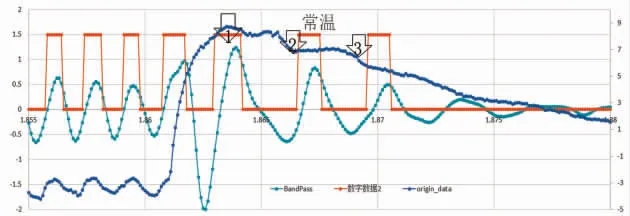
图34 中途停止纹波信号波形处理
车窗电机不同工作温度二值化处理如图35所示。 二值化处理控制模型3在不同温度下, 能分别对电机中途断电工况下的小幅值波形进行有效计数。
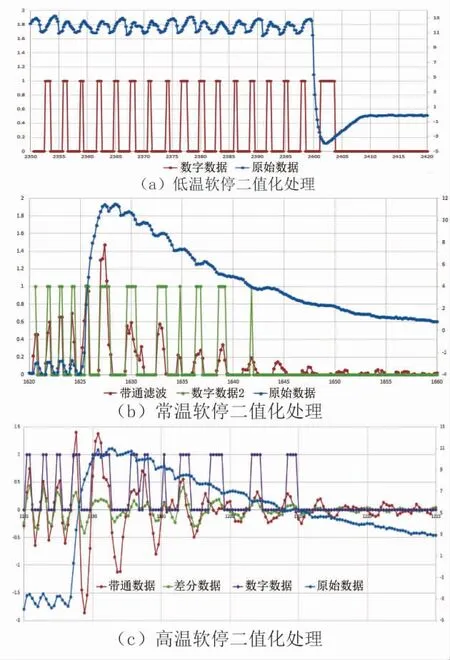
图35 车窗电机不同工作温度软停二值化处理
3.3.1.4 电机堵转工况
堵转工况纹波信号波形周期大, 如采用单一数字二值化控制处理控制模型, 存在丢波问题 (图36), 通过如图37的波形分析, 设计二值化处理控制模型4。
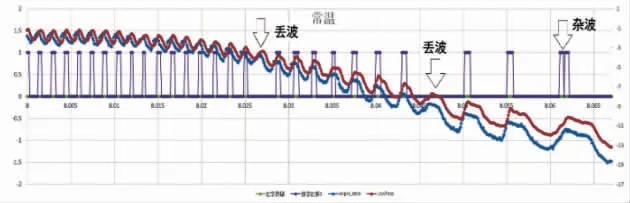
图36 单一数字二值化控制处理丢波、 杂波问题
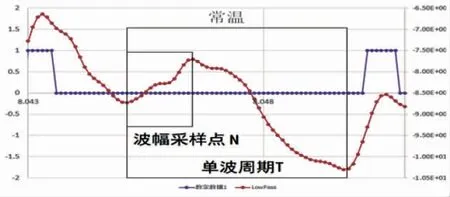
图37 堵转纹波信号波形分析
数字二值化控制处理控制模型4 (N=12, A=0.24):
A=Y(N)-Y(N-12)
A≥A取值1.5
A<A取值0
控制处理后二值化波形如图38所示, 堵转工况下产生的大周期信号能被有效识别, 对纹波数进行修正。
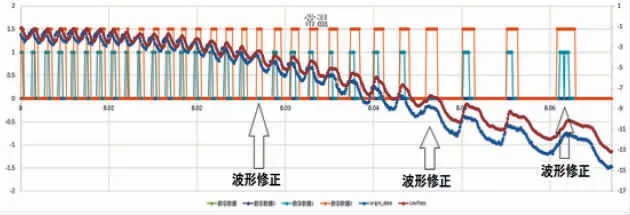
图38 堵转纹波信号波形修正
车窗电机不同工作温度二值化处理如图39所示。 二值化处理控制模型4在不同温度下, 能分别对电机中途断电工况下产生的大周期信号进行有效计数。

图39 车窗电机不同工作温度堵转二值化处理
3.3.2 波形对标
针对不同二值化处理控制模型处理方波结果, 需要进行整体修正处理, 即各方波处理结果需要时间对标修正处理。 本文根据电机工作物理特性设计时间基准判定附标,通过电机上电工作、 断电停止的电流驱动阶跃特性 (图40), 设计二值化处理控制模型5。
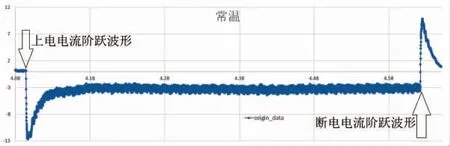
图40 电流驱动阶跃特性
数字二值化控制处理控制模型5 (N=6, A=6):
A=Y(N)-Y(N-6)
A≥A取值2
-A<A<A取值0
A≤-A取值2
控制处理后二值化波形如图41所示。

图41 电流驱动阶跃二值化处理
对上述二值化控制模型处理方波进行综合控制结果如图42所示。 对启动、 断电、 堵转电机纹波波形进行波数修正, 有效解决了电机在启动阶段 (图42a)、 电机中断停止阶段 (图42b) 以及软停堵转阶段 (图42c) 纹波信号丢失导致的电机位置偏差问题。
通过上述波形波数修正补偿处理, 可以整体控制波形波数±1个公差, 实现了纹波防夹电机工作全过程信号采样,从而确保纹波防夹电机位置精确计算, 为系统可靠工作提供信号采集保证。
4 结论
本文介绍纹波防夹原理, 建立了利用纹波确定电机位置的数学模型。 对硬件采集方案进行分析, 对遇到的成本以及滤波互斥等问题, 提出了软件采集方案, 并设计了相应的切比雪夫Ⅰ型低通滤波器, 切比雪夫Ⅰ型带通滤波器对电流信号中的纹波进行提取。 对提取后的纹波在不同温度下, 分别在启动、 稳定、 电机中断、 堵转等工况下设计了二值化处理控制模型, 能有效解决在不同工况下出现的大周期、 小幅值波形等引起的丢波与多波问题, 实验结果表明二值化处理控制模型具有良好的波形计数能力。 该研究成果为后续的纹波防夹过程中的电机位置确定, 提供理论支持。

图42 对启动、 断电停止、 软停堵转阶段波形进行波数修正
