一类变号系数矩阵的代数方程组正解存在唯一性
2022-05-21侯青青刘喜兰
侯青青,刘喜兰
(宝鸡文理学院数学与信息科学学院,陕西宝鸡 721013)
1 引言
本文主要研究形如式(1)非线性代数方程组在系数矩阵变号的情况下解的存在唯一性及正解的存在性.
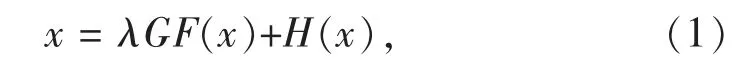
式(1)中λ∈R 上的参数,G=(gij)n×n是n×n 阶系数矩阵,

f,h 是R→R 上的连续函数.系数矩阵为正满足.若gij>0,则G>0(或若gij≥0 则G≥0),∀(i,j)∈[1,n]×[1,n],且
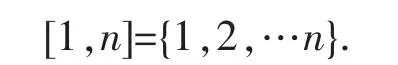
代数方程以及方程组求解是较为复杂的问题,对于非线性代数方程组的求解,在复杂系统、网络、优化和一些其他领域有很广泛的研究和应用[1,2].许多数学问题,如微分方程的数值解、离散边值问题和复杂动力系统的稳态问题都与代数方程组正解的存在性密切相关[3,4],事实上已经有很多文献研究了非线性代数方程组解与正解的存在性和唯一性.如,在系数矩阵为正的条件下,当时,文献[5,6]利用Guo-Krasnoselskii 不动点定理或构造Rn上的一个特殊锥,讨论了方程组(1)解的存在性与正解的存在唯一性.当参数λ=1,H(x)≡0 时,文献[7-9]利用单调迭代法和锥上的不动点定理,讨论了方程组(1)解的存在性与正解的存在性.特别地,文献[10]利用不动点定理讨论了在H(x)≡0 时,方程组(1)正解的存在性.本文讨论了在系数矩阵变号时,方程组(1)解的存在唯一性,及正解的存在性.
2 主要结论
首先给出证明定理的2 个引理.
引理1[11](Brouwer 不动点定理)设X 是Rn的一个非空凸紧子集,T:X→X 是一个连续映射,则T 有一个不动点.
引理2[11](Banach 不动点定理)设(X,ρ)是一个完备的距离空间,T 是(X,ρ)到其自身的一个压缩映射,则T 在X 上存在唯一的不动点.
为了方便起见,以下列出6 个所需条件:
(H1)f,h:R→R 为有界连续函数,即存在正数a,b>0 满足

(H2)f,h 在R 上满足Lipschitz 条件,即存在正常数L1和L2,使得

且0<L2<1;

则方程组(1)的解是算子T 在Rn中的不动点,由此得到定理1、定理2、定理3.
定理1假设条件(H1)成立,则对∀λ∈R,方程组(1)有一个解xλ.
证明对∀λ∈R,定义

则由以上不等式知T:X→X 是一个连续映射,根据引理1 知T 存在一个不动点,即方程组(1)有一个解.
定理2假设条件(H1)和(H2)成立,则当|λ|<λ*时,方程组(1)有唯一的解xλ.
证明令X=[-δ,δ]n⊂Rn,则X 是完备的度量空间.


因此,T:X→X 是压缩映射,由引理2 知T 存在唯一不动点,即方程组(1)存在唯一解.
根据以上证明得到了方程组(1)解的存在唯一性,下面讨论系数矩阵G 与函数H(x)在变号情况下,方程组(1)正解的存在性.
定理3假设条件(H1)和(H3)成立,则当λ<0时,方程组(1)有正解xλ.
证明因为条件(H1)成立,所以由定理1 知,方程组(1)的解存在.
又因为条件(H3)成立,所以存在N>0,当u∈[0,N]时,f(u)>0,h(u)>0,此时


即证得,当λ<0 时,方程组(1)有正解xλ.
类似定理3 可以得到定理4、定理5、定理6.
定理4假设条件(H1)和(H4)成立,则当λ>0时,方程组(1)有正解xλ.
证明因为条件(H1)成立,所以由定理1 知,方程组(1)的解存在.
又因为条件(H4)成立,此时

其中γ 与定理3 中保持一致.
所以存在λ>0,当‖xλ‖∞<δ 时,

即得证,当λ>0 时,方程组(1)有正解xλ.
定理5假设条件(H1)和(H5)成立,则存在μ>0,当λ∈(μ,+∞)时,方程组(1)有正解xλ.
证明因为条件(H1)成立,所以由定理1 知,方程组(1)的解存在.
又因为条件(H5)成立,所以存在N>0,当u∈[0,N]时f(u)>0,h(u)<0,此时
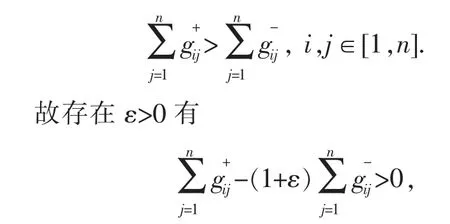
其中γ 与定理3 中保持一致.

即证得,当λ∈(μ,+∞)时,方程组(1)有正解xλ.
定理6假设条件(H1)和(H6)成立,则存在η<0,当λ∈(-∞,η)时,方程组有正解xλ.
证明因为条件(H1)成立,所以由定理1 知,方程组(1)的解存在.
又因为条件(H6)成立,所以存在N>0,当u∈[0,N]时,f(u)>0,h(u)<0,其中γ 与定理3 中保持一致,此时取
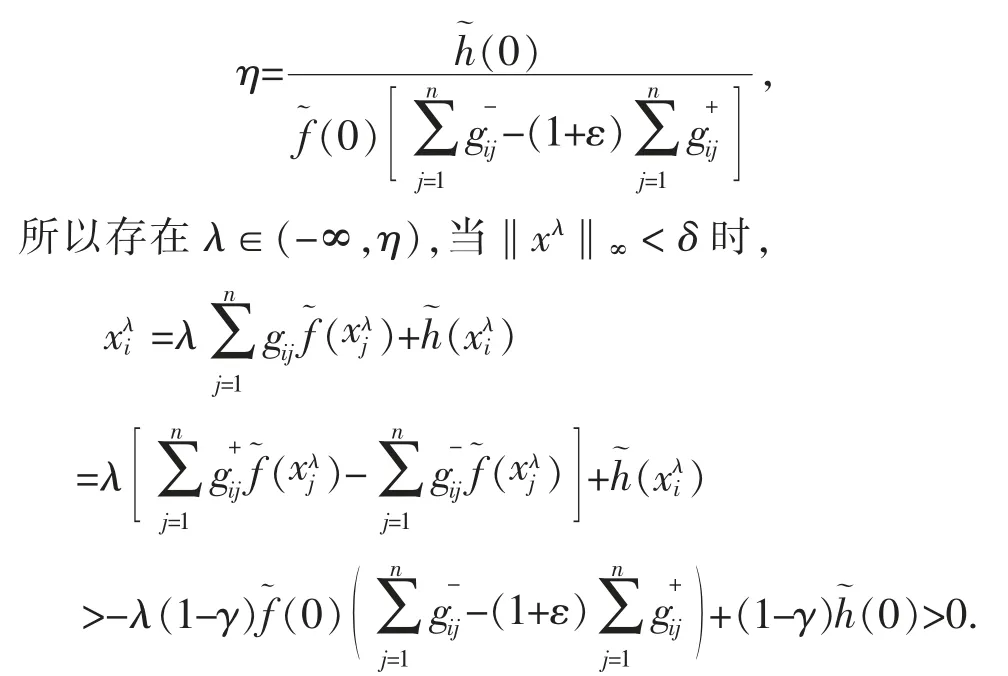
即证得,当λ∈(-∞,η)时,方程组(1)有正解xλ.
