基于同态加密的联邦学习方案研究

梁亚楠

（北京交通大学计算机与信息技术学院，北京 100044）

为了解决数据孤岛问题，McMahan提出联邦学习（federated learning），每个拥有数据源的组织训练1个模型，各个组织在各自的模型上彼此交流沟通，通过模型聚合得到一个全局模型。训练过程中，模型的梯度可能会对用户的隐私造成泄露，采用传统加密手段会使数据加密后失去原有语义，导致训练过程无法进行。

同态加密（homomorphic encryption，HE）技术为解决上述问题提供了思路，由Rivest等在20世纪70年代提出[1]。研究者将支持任何计算方法的同态加密算法称为全同态加密[2]。现有全同态加密算法效率偏低，难以应用到实际场景中；部分同态加密算法只具有加法或乘法一种同态性质，加解密效率较高，被常用于消息传输、数字签名。

1 相关知识

1.1 同态加密的概念

同态加密方法H通常由四部分组成：

式中：KeyGen——密钥生成函数，在非对称加密中，输入密钥生成源g，输出用于加密的公私钥对{pk，sk}=KenGen(g)；Enc——加密算法，将明文m作为输入，输出密文c=Enc(m)；Dec——解密算法，即输入密文c，输出明文m=Dec(c)；Eval——评估函数，将密文c和公钥作为输入，输出与明文对应的密文。

式中：∘——特定形式的代数运算。

1.2 同态加密在联邦学习的应用

同态加密是计算机安全领域和密码学领域的一项热门的隐私保护手段。加密算法需要大量的计算成本，过去仅少量应用于机器学习领域，对隐私保护的需求大于对计算资源的需求时，同态加密逐步被应用到联邦学习中。在联邦学习中，同态加密主要被用于保护客户端上传的梯度。

基于HE的FL的模型训练过程如图1所示。

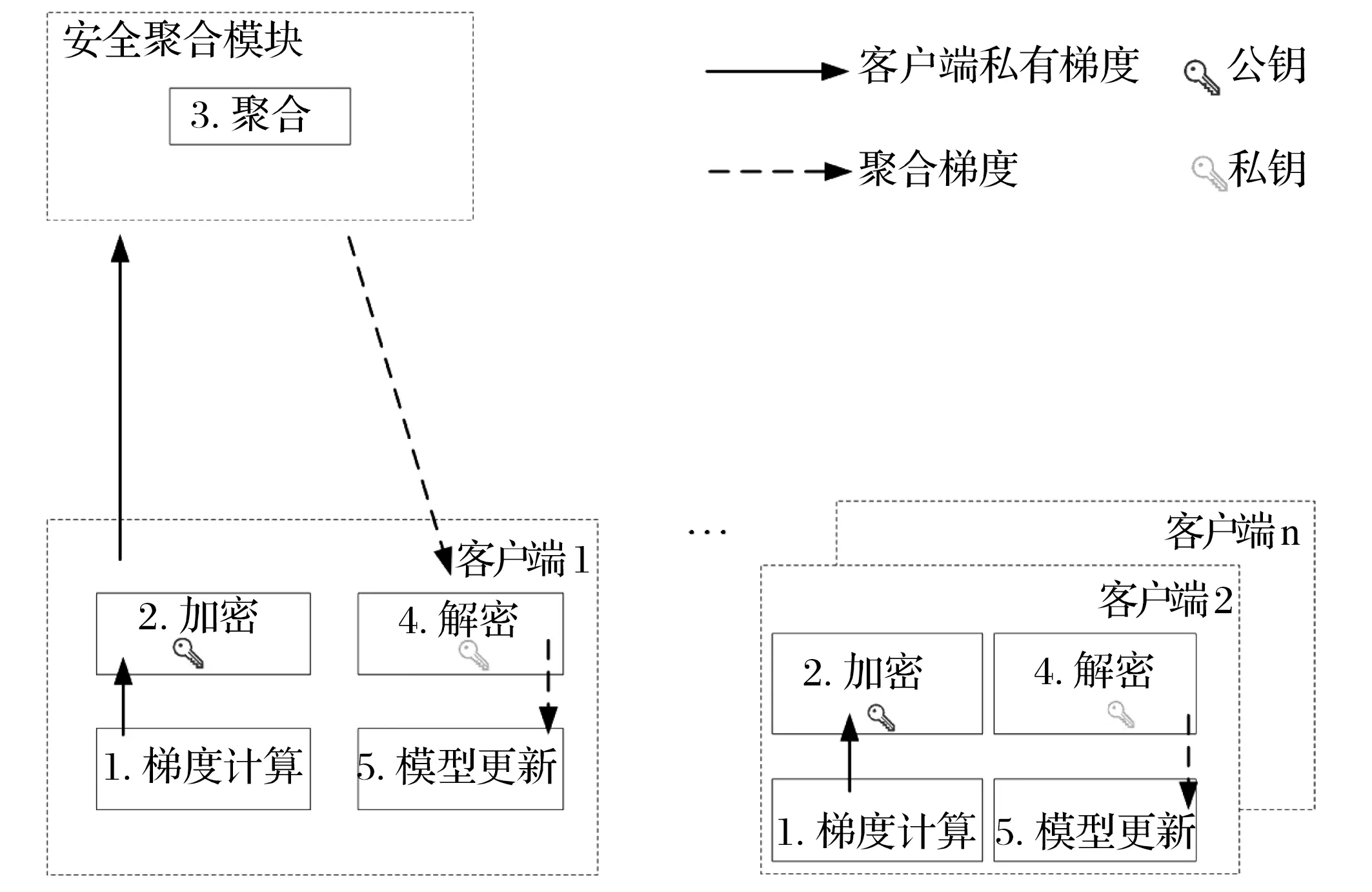
图1 基于HE的FL的模型训练过程

基于纵向联邦学习的隐私保护两方的逻辑回归算法，利用Paillier算法[3]进行安全梯度下降，训练逻辑回归模型，利用Paillier算法的加密的掩码和各方计算得到的中间数据进行加法运算以及常数乘法运算。在安全梯度下降算法中，双方交换加密后的中间结果掩码，将加密的梯度信息发送给协调方进行解密以及模型的更新。

2 基于同态加密的联邦学习方案研究

2.1 基于Paillier的联邦学习方案

在联邦学习的模型中主要考虑两类实体，一类为客户端，包含N个参与训练的用户，作为模型训练但资源有限的一方，为了更高效地达到预期目标，通常在所有参与方确定一个初始模型后（如DNN），在每一次的迭代过程中利用自己的数据集进行训练，将训练样本相对应的梯度权重参数加密后上传至聚合服务器，从服务器发回的结果中解密得到新的参数，更新本地参数。

除了数据聚合的过程外，在训练过程中同样以Paillier半同态加密方案作为安全机制，实现在加密状态下的Logistic Regression训练。

假设有n个样本数据集：

LR的对数损失函数，明文状态为：

损失函数值L关于模型参数θ的梯度满足：

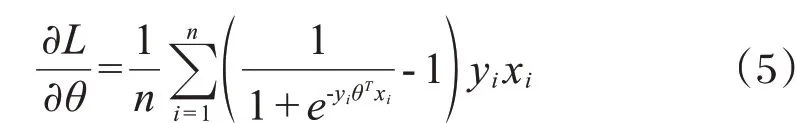
利用梯度下降，求出每一步的参数更新：

参数θ和数据(x，y)均在明文状态下计算，联邦学习场景中存在数据泄密的风险，基于HE的联邦学习要求在加密的状态下进行参数求解，传输的参数θ是一个加密后的值[[θ]]，将损失函数改写为：

而在上述过程中，Paillier加密算法只支持加法同态和标量乘法同态，不支持乘法同态和复杂的指数、对数运算，无法在加密状态求解。文献[4]提出一种Taylor损失近似原始对数损失的方法，将原始的对数损失函数进行泰勒展开，使用多项式近似对数损失函数，损失函数转化为只有标量乘法和加法的运算，利用Paillier进行加密求解。

使用二阶多项式近似对数损失函数，将z=yθTx代入泰勒展开的损失函数：

y2=1，因此直接去掉y，将式（6）代入式（2）：

对（9）求导，得到损失值L关于参数θ的梯度值：

得到加密梯度：

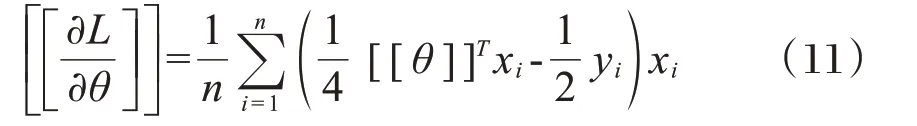
2.2 基于CKKS同态加密的优化方案

本方案采用CKKS同态加密方案，CKKS加密方案是基于LWE困难问题的同态加密方案，与Paillier同态加密方案相比，此加密方案保有加法同态性质以及有限次乘法同态性质，使得加密结果不会出现影响训练结果的误差。

若双方的向量内积计算有两个，参与方A，B各有一个向量VA={a0，a1，...，an}，VB={b0，b1，...，bn}，要求计算两个向量的内积，且不泄露各自的隐私

A 使用自己的公钥（CKKS 算法）加密数据EncA(VA)，将密文发送给B；B用A的公钥（CKKS算法）加密数据EncA(VB)；B计算C0=EncA(VA)EncA(VB)=EncA(a0·b0)，…，EncA(an-1·bn-1)；B对C0移位得 到C'0，求和得C1=C0+C'0；B对C1移位得到C'1，求和得C2；B得到最终结果，将其发送给A；A解密得到结果。

Paillier算法中，需要泰勒展开以计算近似损失函数，计算量大。CKKS可以使用公式（2）直接对加密参数θ和数据(x，y)进行运算。CKKS引入rescaling，使同态计算期间，编码前后的消息大小保持基本不变，保证方案所需的最大密文模数随运算电路深度呈线性增长，极大地提高方案的效率。

3 性能分析

基于FATE的试验框架下，使用乳腺癌数据集[5]作为训练数据，在同态加密下进行联邦学习训练模型，本地训练的每一轮迭代中，随机挑选固定大小的训练数据进行训练。

同态加密联邦学习训练的模型准确度如图2所示。

图2 同态加密联邦学习训练的模型准确度

结果表明，采用CKKS加密方案可以节省时间，在保证用户隐私的情况下达到近似的准确率。

4 安全性分析

根据联邦学习的隐私需求，在“诚实且好奇”[6]的聚合服务器下，必须保证用户个人数据的私密性。本方案满足联邦学习环境下，各参与方协作训练所有功能需求，可以保证安全性。

假设4.1：针对“好奇”的服务器，系统模型是安全的。“诚实且好奇”的服务器不了解有关参与方本地数据集的任何信息，服务器不能从加密的权重参数中得到梯度的信息。

服务器是诚实的，即服务器会按照参与方的要求以及训练的流程正常执行相关操作，且“好奇”的服务器会分析处理其收到的加密过的密文信息。如果加密过的密文能够抵抗选择明文攻击，则不会从密文获得任何信息，证明其是安全的。

方案中，传输到服务器的有关参与方的相关信息通过CKKS加密方案加密，CKKS加密方案能够抵抗选择明文攻击证明其是安全的。而CKKS同态加密方案是基于LWE问题[5]的同态加密算法，LWE是基于格上的困难问题，是求解带噪声的线性方程组问题，LWE问题尚无有效的量子求解算法，基于LWE假设的加密方案被认为是抗量子的，证明设计方案是安全的。

基于同态加密的联邦学习框架如图3所示。

图3 基于同态加密的联邦学习框架

5 结语

针对在联邦学习的环境下，本文研究用于保护用户隐私的数据聚合方法，使用基于LWE问题的CKKS同态加密方案，可以提升计算效率，具有安全性。

但方案仍存在一定不足，针对用户数据方面，参与方所提供的数据质量较差会影响训练效率；用户在参与过程中掉线，可能无法得到想要的效果。未来将在解决数据异质性以及鲁棒性上进行进一步的研究，考虑进一步提升计算效率。