一种城市公共自行车系统调度优化模型
2022-05-21邵卿
邵 卿
(湖南铁路科技职业技术学院,湖南株洲 412000)
城市公共自行车系统有助于解决城市交通拥堵和公共交通出行“最后一公里”难题,但系统运转过程中需要解决车辆的周转调度问题。蒋塬锐等[1]针对共享单车供需失衡、共享率低等问题,以提高用车高峰期调度的及时性为目的,在调度结构中引入调度池,明确调度池的使用规则,提出共享单车四级调度结构,考虑节点的调度需求大于调度车的装载容量和多辆调度车共同满足单个节点的调度需求的情况,以调度总成本最小为目标,建立共享单车静态调度模型。李军等[2]将公共自行车顾客借、还车辆的过程看作排队现象,完整描述排队系统的输入、输出过程及排队规则和服务方式,利用实例车辆借还数据,标定顾客借还车的到达及站点服务时间均服从负指数分布,基于损失制排队系统效率指标计算方法,建立站点最优化车辆调配数(空桩数)计算模型。李迎晨等[3]提出基于遗传算法的公共自行车高峰期调度模型,可以满足早晚高峰居民出行的自行车需求。高亮等[4]为提高公共自行车系统调度效率并降低调度成本,提出基于预测库存变化率的公共自行车动态调度方法,建立优化目标为车辆总行驶距离最短的动态调度模型。于德新等[5]针对现有自行车调度模型假设条件的局限性,提出共享经济模式下转运最大化策略,在详细分析共享单车调度成本及相关参数的基础上,以成本最小和投放率最高为目标建立共享单车调度模型,引入精英策略和进化算子对遗传算法进行改进,采用TOPSIS法在改进算法求解出的有效路线集中选择最优路线。
1 模型构建
模型规划描述了确定待建租赁点和各点的调配量的情况下,规划调度车辆的路线安排和分配,使总运输成本最小。待建的站点编号被定为j(j∈J1),将车场编号定为0;设运输车辆编号定为v(v∈V),建立模型:),目标为总运输成本最小,包括固定成本和可变成本。
设定约束条件:
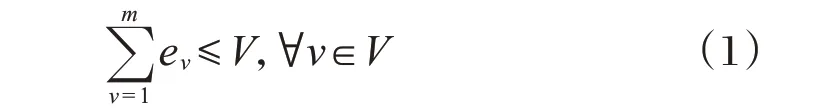
限制调度车数量。
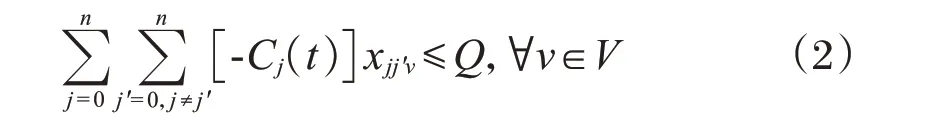
限制调度车的运输容量。
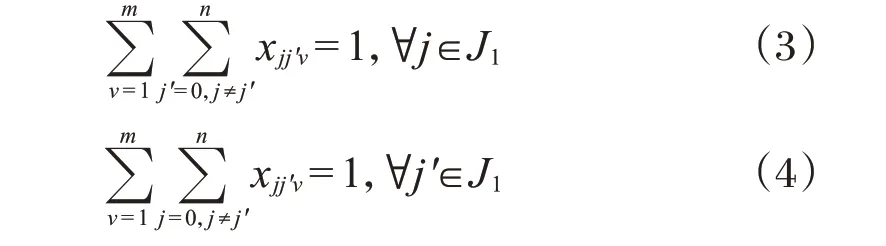
各站点都被服务,且一辆车仅服务一次。

车辆v为租赁点j调度服务的决策变量,车辆v在租赁点j′结束调度工作后,再到租赁点j进行调度,则xjj′v=1,否则xjj′v=0。

运输车辆v运输路径的决策变量,若车辆v被使用,则ev=1,否则ev=0。
2 算例分析
2.1 算例简介
拟在某规划区域内建设一个公共自行车租赁系统,进行自行车调运工作,根据居民的出行需求确定10个自行车出行需求点,分配相应数量的自行车和停车桩,以满足居民的出行需求,做到任一时段居民在其步行范围内的租赁点均能够借到车和还出车,使规划区域内居民总出行时间最短。但租赁点的建设数目应为7~13,避免租赁点建设太多造成资源的浪费以及租赁点建设过少无法满足出行者的需求。
候选租赁点和需求点之间的距离如表1所示。
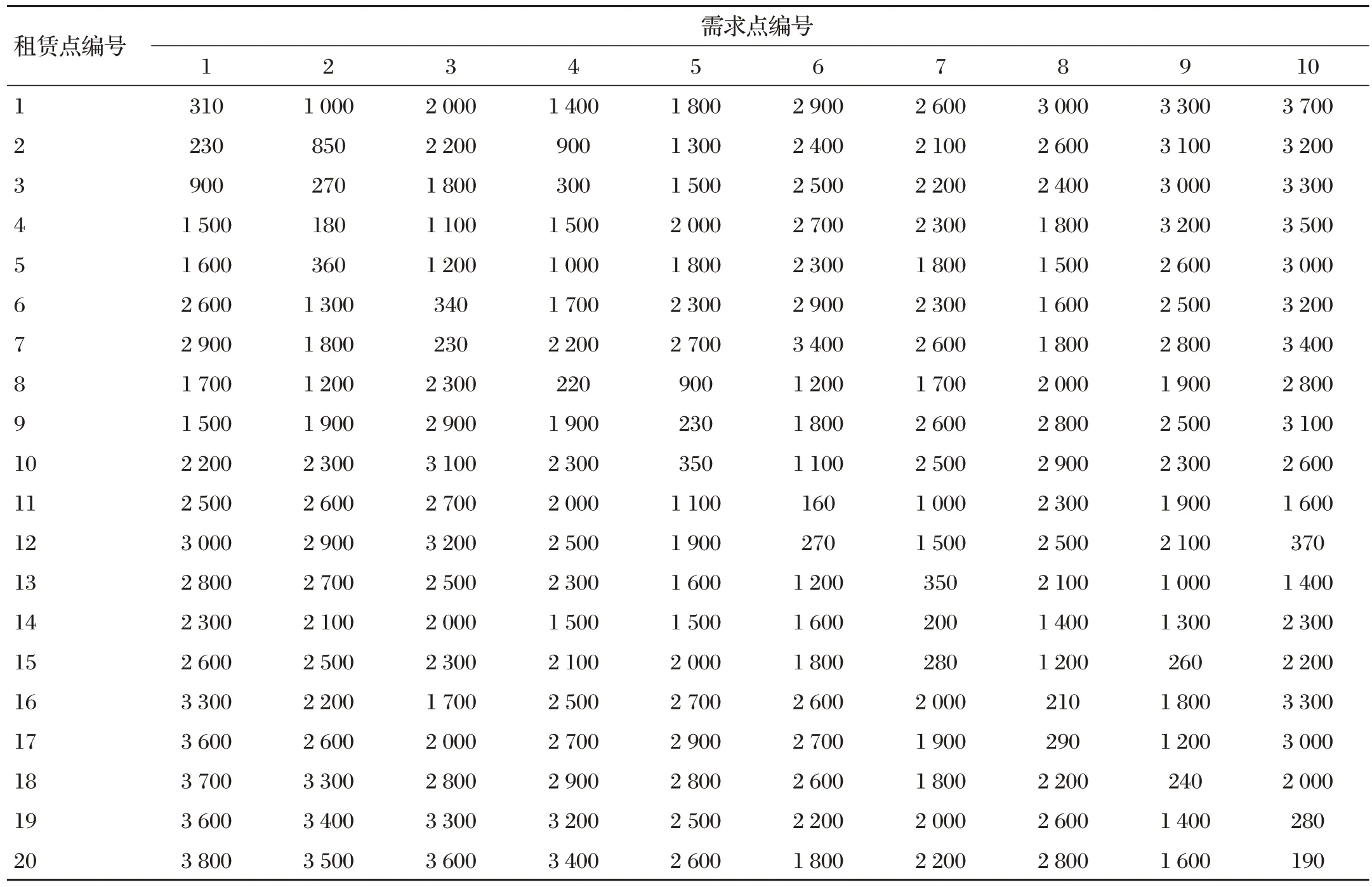
表1 候选租赁点和需求点之间的距离 单位:m
时段1各个需求点的公共自行车租借需求如表2所示。
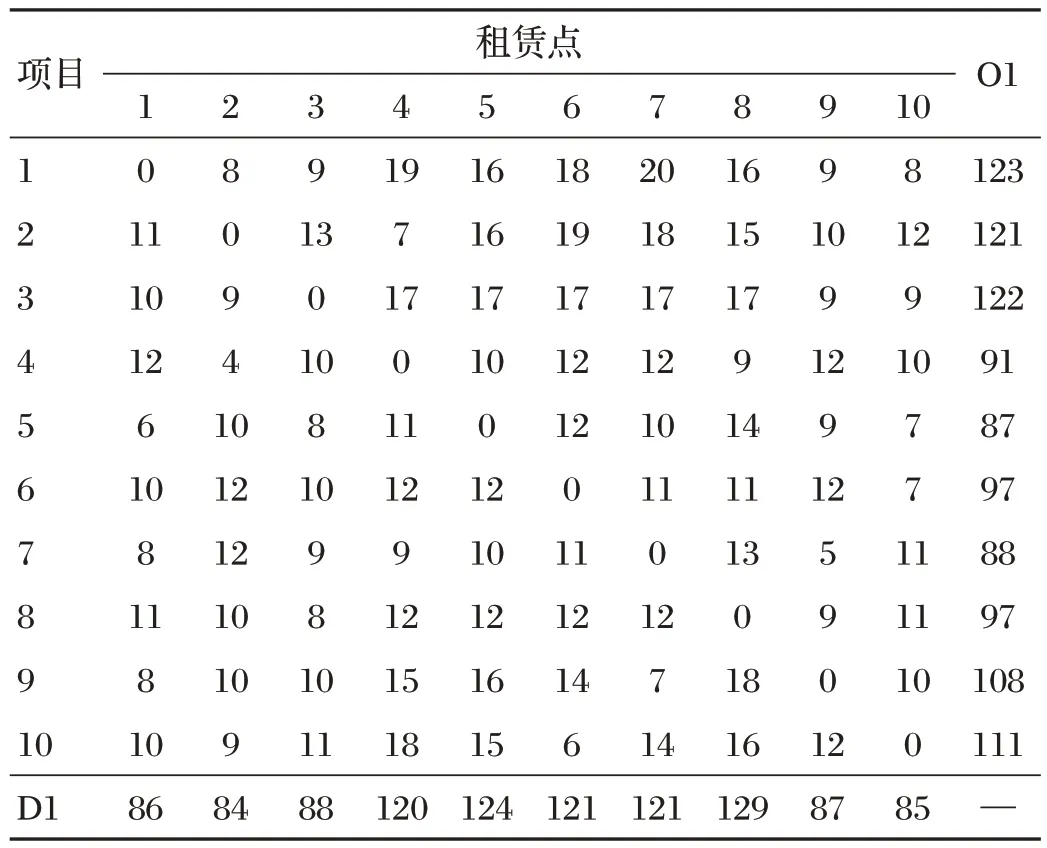
表2 公共自行车租借需求
算例运算思路逻辑图如图1所示。
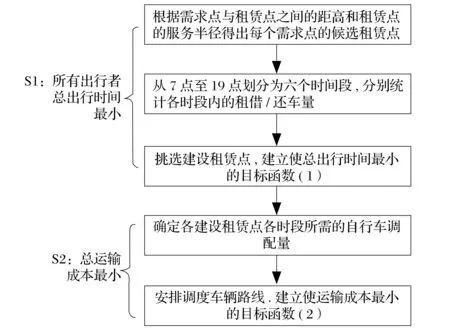
图1 算例运算思路逻辑图
2.2 算例求解
(1)相关常量取值。
C=400 m、M=10 000、g=50 000元、α=15辆、f1=300元、f2=2 000元、v1=1.4 m/s、v2=5 m/s、V=2辆、p=2元/km、r=40元、Q=100辆。
(2)根据租赁点与需求点间的距离以及租赁点的服务半径C可得每个需求点对应的候选租赁点。
需求点对应的候选租赁点如表3所示。
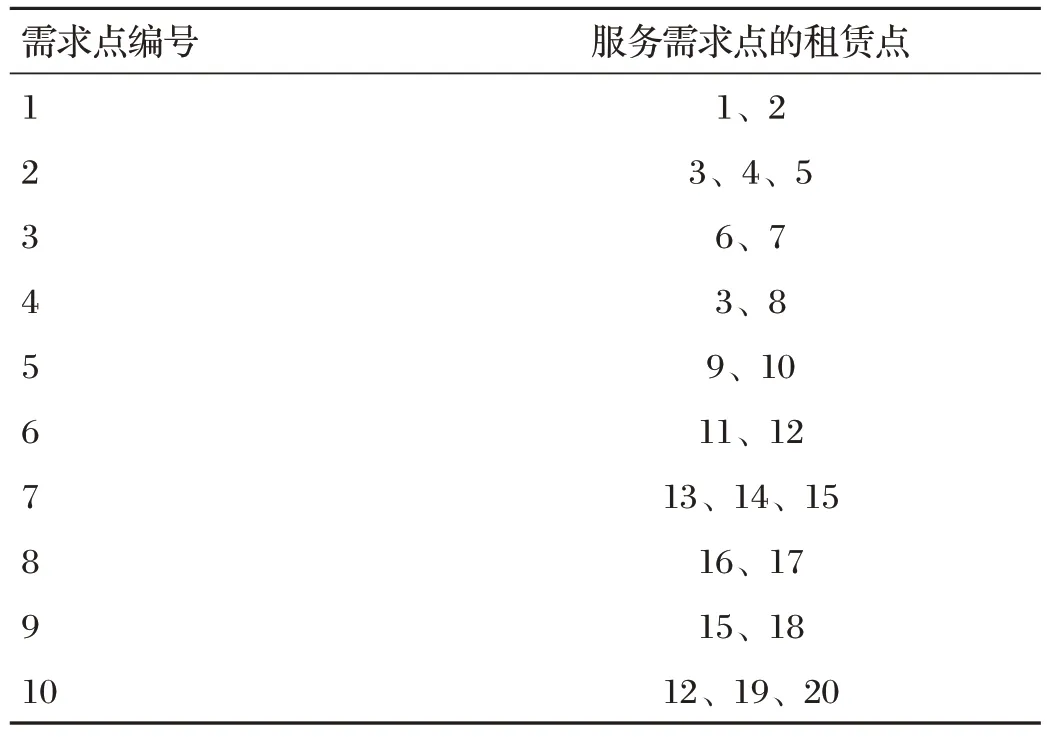
表3 需求点对应的候选租赁点
(3)运用LINGO编程求解,运行该程序计算规划区域内居民最短的总出行时间为4 096 021秒,运输成本为363.5元,共需建设13个租赁点,编号分别为2、4、6、7、8、9、11、14、16、17、18、19、20。
租赁点应分配的自行车数和停车桩数如表4所示。
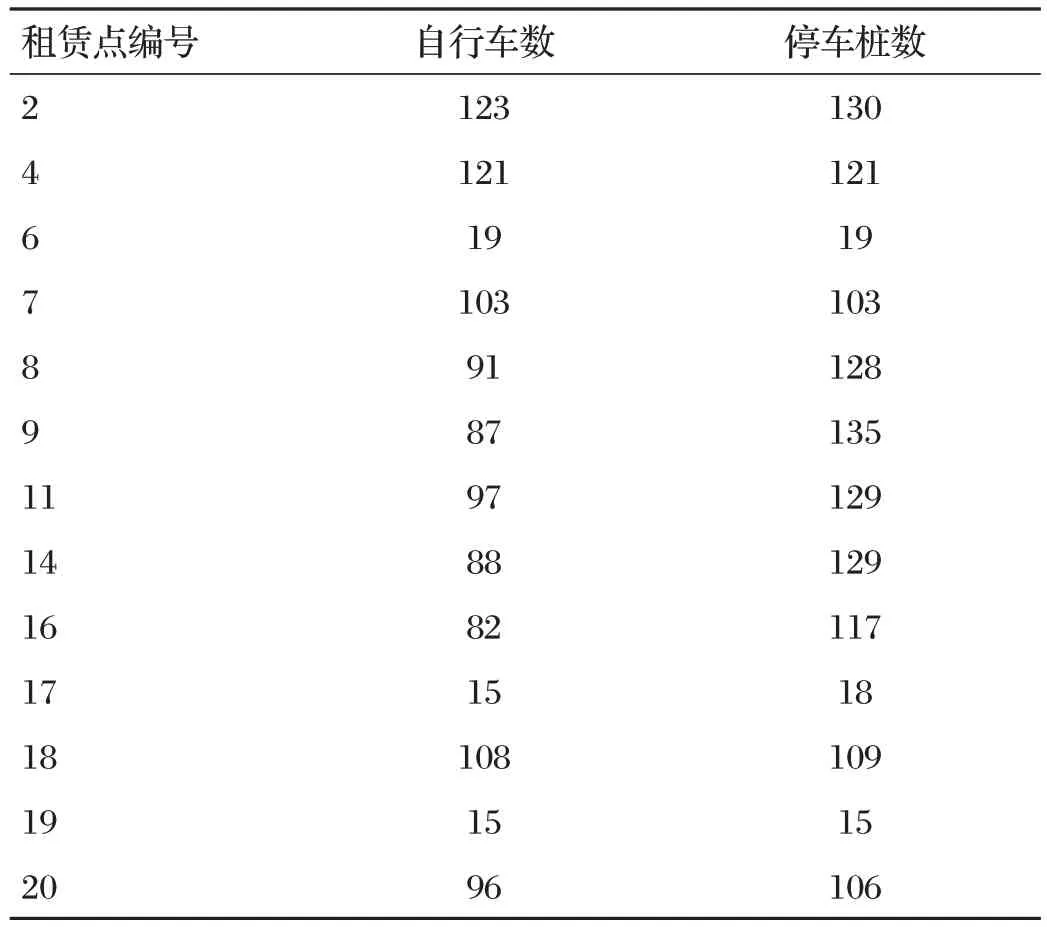
表4 租赁点应分配的自行车数和停车桩数
依据选址方案及租赁点和需求点之间的距离表可得到各建设的站点应服务的需求点和调度车辆路径。调度车辆运行路径为2→4→6→7→16→17→14→18→19→20→11→8→9。
各租赁点各时段的调配量见表5。
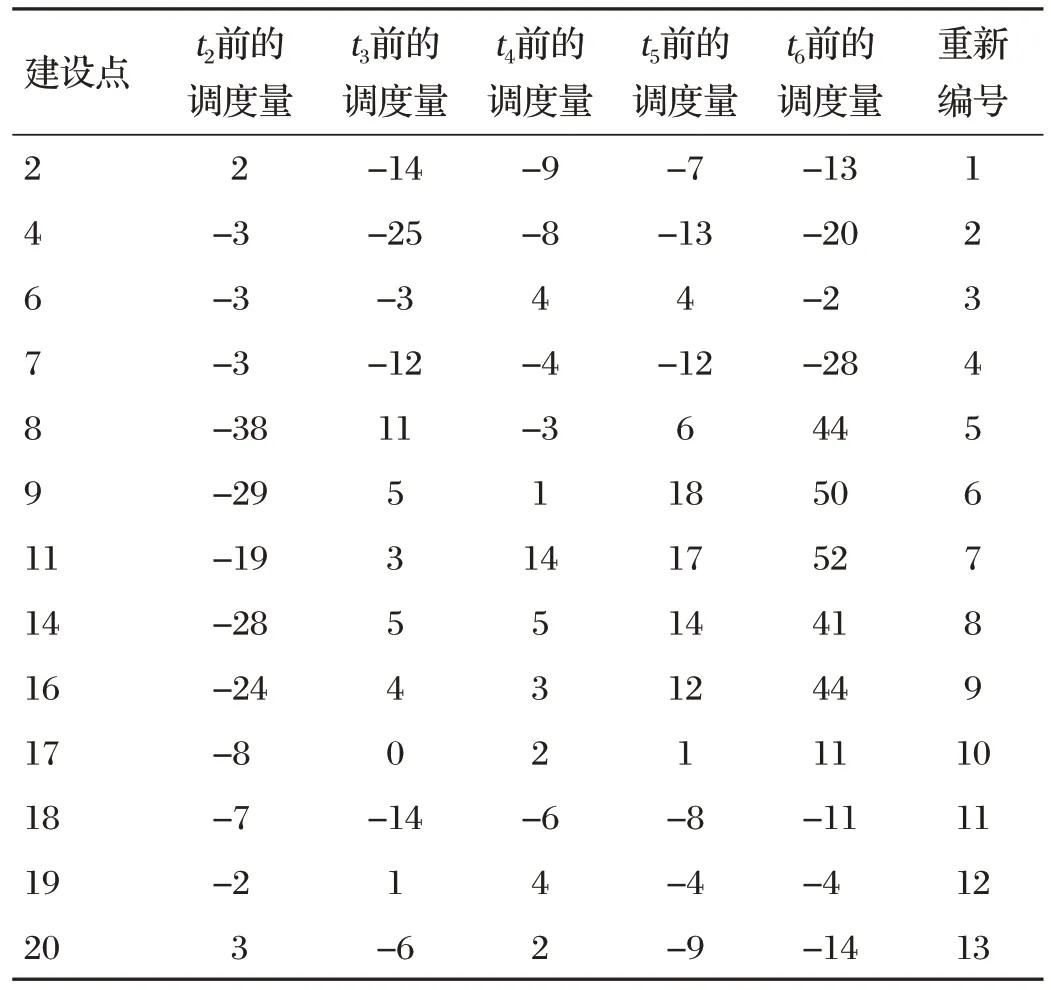
表5 各租赁点各时段的调度量
租赁点服务需求点和调度车辆路径如图2所示。
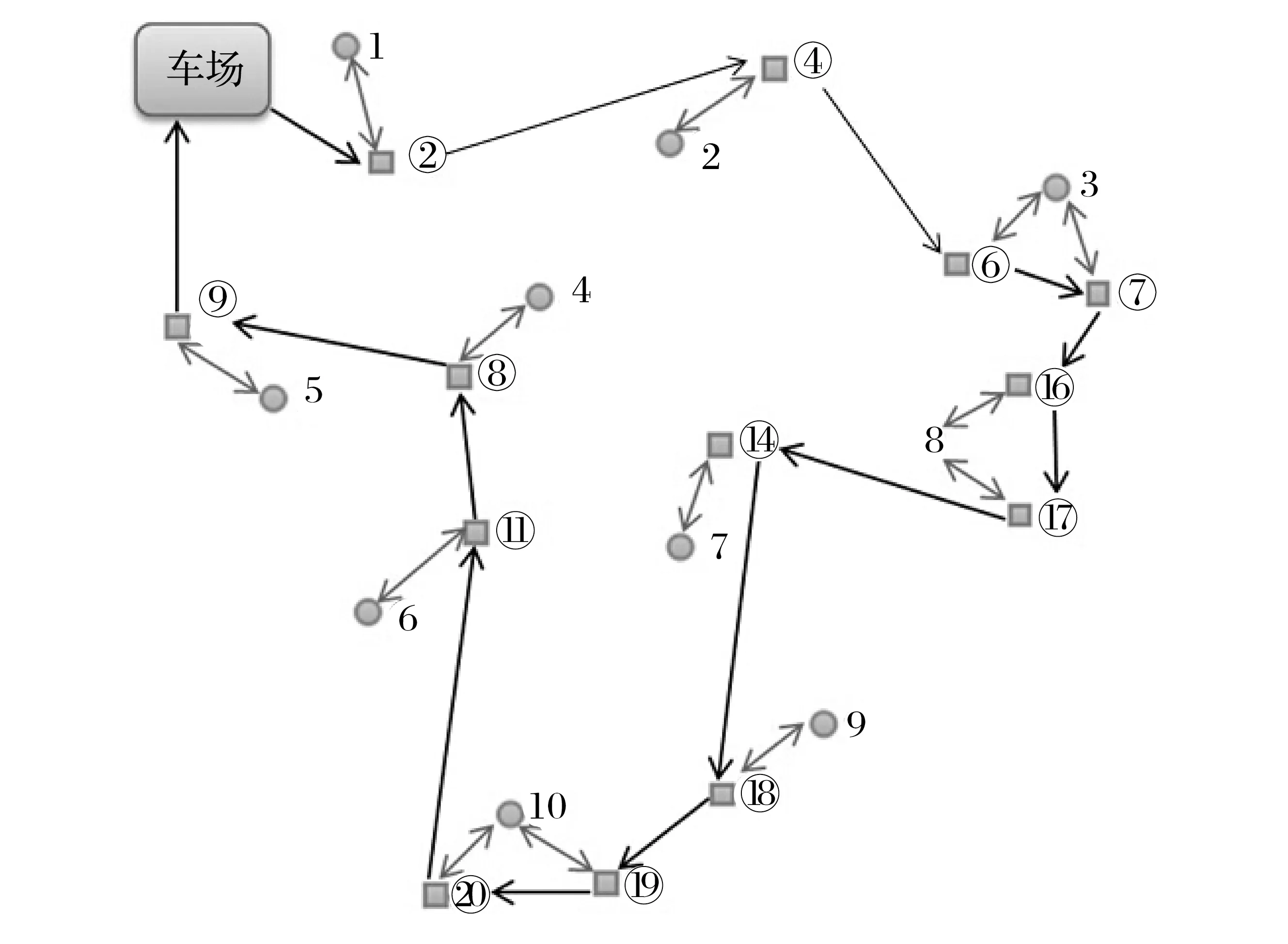
图2 租赁点服务需求点和调度车辆路径
3 结语
本文研究城市公共自行车系统调度优化问题,基于问题分析建立相关的函数关系,构建公共自行车调度优化模型供科学决策参考,未来可以考虑将研究对象的范围由本文适用的小区扩大至街区。
