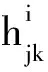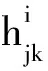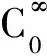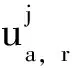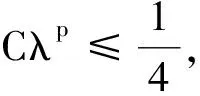一类线性椭圆型偏微分方程组解的边界正则性
2022-05-21杜厚维向长林
杜厚维,向长林
1.长江大学信息与数学学院,湖北 荆州 434023 2.三峡大学三峡数学研究中心,湖北 宜昌 443022
1 引言
考虑如下椭圆型偏微分方程组解的边界正则性:
-Δu(x)=Ω(x)·u(x)x∈B
(1)
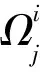
上述方程组可以用分量表示为:

(2)
上述分量表示使用了Einstein求和约定:重复指标代表求和。
方程组(1)可以用来线性化很多具体的几何偏微分方程,这是因为具体的几何偏微分方程通常是非线性的问题,研究起来非常困难。例如,假设u=(u1,…,um)是从B映射到N的调和映照,N是等距嵌入到Rm中的光滑黎曼流形,则调和映照方程可以表示为:
式中:A(u)代表靶流形N在Rm中的第二基本形式。以ν代表流形N的法丛的一组标准正交基,只需要取:

则上述方程可以写成式(2)的形式。又如,假定u:B→R3满足预定平均曲率方程:
-Δu=-2H(u)∂xu∧∂yu
(3)
式中:H代表预定的平均曲率。直接验证可知式(3)可以写成方程组(2)的形式,只需要取:
对于上述的几何偏微分方程,通常无法直接得到光滑的解,因此优先考虑的都是弱解的存在性,此时需要付出正则性的代价,即弱解的光滑性一般来说比较差。由此带来的一个基本问题就是提升解的正则性,即证明弱解事实上恰是想要得到的光滑解。这里的一个显然的困难在于方程组(1)的右端的低正则性。由假设可知右端Ω·u∈L1(B),这使得该问题恰好处于经典的椭圆方程Lp理论的端点p=1上,从而无法直接使用Lp理论去提升正则性。而且,FREHSE[1]的下述反例表明,如果仅仅假设Ω是平方可积函数,则弱解可以不连续:令m=2,u=(u1,u2)是从平面上的单位圆盘B1(0)⊂R2到单位圆周S1⊂R2的映射,定义为:
直接验证可知u∈W1,2(B1(0),R2)是方程(1)的解,其中Ω定义为:
此时解属于L∞但是不连续。因此,一定要求具有额外的好性质,才能够保证解的连续性。譬如,RIVIRE[12]通过略微加强Ω的可积性,即假设Ω属于Lorentz空间L2,1,就能够证明方程组(2)解的连续性。但是这个里面的一个缺陷是,在应用到实际问题中时,难以保证Ω属于Lorentz空间L2,1。
在开创性的工作[11]中,RIVIRE发现,不仅仅是调和映照方程与平均曲率方程,而且平面上所有的椭圆型共形不变的Lagrange泛函的临界点都可以写成方程组(1)的形式,其中Ω是平方可积函数,且Ω具有额外的代数结构:
即此时Ω还是反对称矩阵。因此,RIVIRE假设方程组(1)中的Ω平方可积且具有反对称性。在该假设下,RIVIRE创造性地应用UHLENBECK[15]的分解方法,证明方程组(1)满足守恒律,并且具有Jacobian结构,从而可以利用Hodge分解与积分补偿理论[1]证明解的连续性。这一结果同时解决了共形几何中的两大猜想。特别的是,RIVIRE的这一工作以大不相同的方法再次得到了HELEIN[6]关于二维弱调和映照连续性的著名结果。反对称性是RIVIRE非常关键的一个假设。有反例表明,如果Ω是对称矩阵,则弱解可以是不连续(甚至是无界)[11]。RIVIRE与STRUWE[13]进一步把文献[11]中的主要结果推广到了高维情形。
(4)
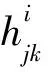
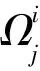
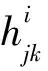
则方程组(1)的每一个解都是局部Hölder连续的。
上述文献讨论的是解在区域内部的连续性问题,即内部正则性,解的整体正则性是与内部正则性同样重要的一个问题。要得到整体正则性,必须要建立边界正则性。譬如,考虑平面有界区域上的薄膜,固定其边界,则薄膜具有最小能量的状态对应于区域上的调和函数。很自然的问题是:薄膜在边界会有断裂的点吗? 或者调和函数能够连续到区域的边界去吗?又如,RIVIRE的工作[11]留下一个自然的问题:假设u是方程组(1)的弱解,并且具有连续的边值,那么解是整体连续的吗? 在假定Ω满足与文献[11]同样的条件下,MÜLLER与SCHIKORRA[10]对这一Dirichlet边值问题给出了肯定的回答。他们利用Gauge变换重新改写方程,从而得以改进RIVIRE[11]的连续性结果,并证明了解在区域内部的局部Hölder连续性,最后再通过比较原理等方法得到边界附近的连续性。同样地,在LAMM与RIVIRE关于四阶椭圆方程组的研究[7]中,他们用守恒律的方法建立了解的内部连续性,但是没有得到Hölder连续性与边界正则性结论。最近,GUO等[2]用衰减估计的方法把文献[7]的连续性结果改进为局部的Hölder连续性,并利用比较原理等方法证明了该四阶方程组两类边值问题的边界正则性。对于某种特定的四阶以上的临界增长的高阶非线性椭圆方程组,LAMM和WANG[8]也建立了类似的边界正则性结果。
文献[5]考虑了方程组(1)解的内部正则性,但没有考虑带有边值的整体正则性问题,为此,笔者考虑方程组(1)在条件(4)下的边界正则性问题。
2 主要结论
令1≤p≤2,a∈B,r>0使得Br(a)⊂B,其中Br(a)表示以a为中心r为半径的开圆盘。定义:
(5)
文献[5]不仅证明了解的连续性,而且证明了如下的估计:存在与解无关的常数p∈(1,2),C>0,R0>0,μ>0,使得对方程组(1)的任意解u,任意的a∈B,只要0 R0,1-|a| },都有: (6) 记Br(x0)⊂R2表示平面上以x0为心r为半径的开圆盘,Lp(D,Rm)表示区域D上的取值于Rm中的p次可积函数的全体,它的范数为: W1,p(D,Rm)是标准的Sobolev空间,f=(f1,…,fm)∈W1,p(D,Rm)表示每个分量fi(1≤i≤m)是区域D上的p次可积函数,且具有p次可积的1阶弱导数,它的范数定义为: 用: 表示函数u在区域D上的振幅。用字母C表示各种不等式中出现的常数,它的大小可以随着出现位置的不同而不同。 引理1令x∈B,r=dist(x,∂B)>0。则对任意的映射u∈W1,2(B2r(x)∩B,Rm),都存在r1∈(r,2r)使得u∈W1,2(∂Br1(x)∩B),且: 证明由Fubini定理有: 该不等式意味着,存在r1∈(r,2r),使得u∈W1,2(∂Br1(x)∩B)。再由Sobolev嵌入: W1,2(∂Br1(x)∩B)⊂C1/2(∂Br1(x)∩B) 即可得到引理1中的估计。 下面的局部最大值原理是证明定理1的关键估计,笔者采用文献[8]中定理3的方法。 引理2令u∈W1,2(B,Rm)是(1)的一个弱解,且假设Ω满足定理1的条件。若u在∂B上等于某个连续函数g∈C(∂B),则存在C>0使得对任意的x∈B,R>0,q∈Rm,都有下述估计成立: 式中:DR(x)=B∩BR(x)。 M≥‖u‖L2(D4R(x)) 否则结论自动成立。由M的定义,可以选取x0∈DR(x),使得: (7) 令r0=dist(x0,∂DR(x))>0。则Br0(x0)⊂DR(x),并且对任意的0 (8) 接下来用引理1可以找到r2∈(r0,2r0)使得: osc∂Br2(x0)u≤C‖u‖L2(B2r0(x0))≤C‖u‖L2(D4R(x)) 注意到Br2(x0)∩∂DR(x)≠Ø。用(r,θ)表示以x0为中心的极坐标。则对任意的θ∈S1,只要(r1,θ),(r2,θ)∈DR(x),就有: 对所有的θ取下确界,得: ≤C‖u‖L2(D4R(x)) 因此,用式(8)与上述估计,对任意的x*∈∂Br2(x0)∩DR(x),可得: 想要的估计从上述不等式即可得到。 证明令u是方程组(1)的一个弱解,且Ω满足定理1的条件。假设u在∂B上等于某个连续函数g∈C(∂B)。令x0∈∂B,q=g(x0),由积分的绝对连续性,对任意的ε>0,都可以找到R>0使得: 从而存在r1∈(R,2R)使得: 于是,由引理2有: 由g的连续性可知,上述不等式蕴含了u连续到边界。 推论1假定u∈W1,2(B,R3)是平均曲率方程(3)的弱解,若H∈L∞∩W1,2(B)且u在边界∂B上具有连续的边值,则u连续到边界。 假设B是一个单位圆盘,在这种情形下,区域内部到边界可以由射线连接,因此可以不需要极大值原理。 证明应用与文献[14]类似的方法证明。为简便起见,记S=∂B,S(r)=∂Br。对r∈[0,1],ω∈S及x=rω∈S(r),记: υ(r,ω)=u(rω) 固定y0=ω0∈S,令x=ρω是B的内点且靠近y0,ρ非常接近1。令δ=1-ρ,令σ是一个待定的非常小的正数,用Cσ表示顶点在原点的锥,锥的张角为σ,锥开口方向的中线与ω0相同。假设x∈B∩Cσ,选取一个点x′=ρω′∈Bδ/2(x)∩Cσ,其中方向ω′∈S将在随后选取。由三角不等式得: |u(x)-g(y0)|≤|u(x)-u(x′)|+|u(x′)-g(ω′)|+|g(ω′)-g(y0)| (9) 由假定,g是S上的连续函数,这意味着当δ与σ都很小时,不等式(9)右端的第3项随之变得很小。由式(6)与Hölder不等式可知: 因而当δ→0时,不等式(9)右端的第1项也将趋于零。因此,只需证明当δ与σ很小时,不等式(9)右端的第2项也很小即可。 为此应用文献[14]的想法,该想法本质上依赖于Sobolev映照的ACL性质。对任意的σ∈(0,π): 从而: 再用反证法即知存在一个具有正测度的集合Eσ⊂(Cσ∩S),使得: 假设: 对所有这样的θ成立,现在可以证明(9)右端的第2项很小: 其中ω∈Eσ。选取σ=cδ(注意到H1(Cσ∩S)≈σ)和ω∈Eσ,从上述估计可以得到: 当δ→0时,定理3得证。 由于文献[5]已经证明了估计式(6),因此定理2是定理3的一个简单应用。 文献[5]通过选取非常高明的试验函数,用一个比较初等的方法证明了定理1。笔者在此给出定理1的另外一种初等证明。 由MORREY的Dirichlet增长定理(见文献[4]),只需要证明引理3,则定理1自然成立,详细的证明见文献[5]。 引理3设u是方程(1)的弱解,且定理1中的条件成立。记: 则对任意的p∈(1,2),都存在只依赖于p和H以及系数υ常数λ∈(0,1),r0>0,使得对任意的a∈B,0 (10) 证明1)任取开球Br(a)使得B2r(a)⊂B。在球Br(a)上把u分解为2个部分u1,u2,其中u1是球Br(a)上的调和函数组,在边界∂Br(a)上等于u,u2=u-u1。则u2满足方程: 2)估计u2。由于u2在边界∂Br(a)上等于零,故存在一个只依赖于p的常数C>0使得: (11) (12) (13) 于是,由u2的方程及分部积分公式得: (14) 这里的第1个、第2个不等式用到了哈代空间H1(R2)与有界平均振荡空间BMO(R2)的对偶关系,其中⊥υk·(φi)∈H1(R2),且: 证明见文献[14]。第3个不等式利用了式(12)和式(13): 这里的常数C还依赖于H。 因此,在不等式(14)中对φ取上确界,由式(11)可得: (15) 式中:C是一个只依赖于p,H的正常数。 3)对u作估计。λ∈(0,1)待定,有: 上述第1个不等式利用了调和函数的增长估计,证明见文献[4]; 最后一个不等式由式(15)得到。从而: ≤C(λp+λp-2‖υ)Mp(a,2r;u) 从而结论成立。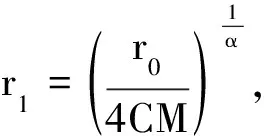
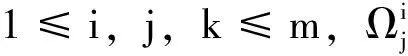
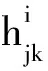
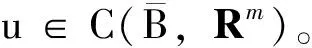
3 定理1的初等证明