弹性需求下带可交易电子路票的交通网络多目标双层规划模型

吕一兵，肖扬，王潇

长江大学信息与数学学院，湖北 荆州 434023

城市交通系统支撑着社会经济的快速、有序发展，同时也决定着人们的日常生活质量。随着全球城市化进程的不断加快，汽车产业快速发展，全球范围的交通拥堵和车辆尾气排放问题已对社会、经济和环境造成了一系列负面影响。发展可持续性交通，是我国交通未来的大趋势。因此，研究交通运输的可持续性在当代城市快速发展过程中的重要性越来越凸显。

交通运输的可持续发展关键在于如何缓解交通拥堵的现状和降低交通系统运行所带来的尾气排放。一般来说，有2类缓解交通拥堵的办法：一是增加道路供给，二是降低交通需求[1]。增加道路供给是最简单、最直接缓解交通拥堵的方式，但由于目前国家的空间资源的占用率较高，土地资源并不是无止境的，不能单单依靠占地修路的方式缓解交通拥堵的现状。而且，盲目提供交通设施已经被证明是适得其反的策略。另外，政府投资在交通运输方面的资金有限，增加道路供给又会诱导出行者更多出行需求，所以仅仅增加道路供给不足以缓解交通拥堵的现状，而将上述两种手段结合起来，可望更有效地缓解交通拥挤。

增加道路供给的方法主要有2种：价格手段和数量手段，具体有新修路段、改建旧路、红绿灯优化、更新交通工具等[2]。长期以来，道路收费被认为是缓解交通拥挤的有效价格手段，其既可以引导和调节交通需求，提高收费区域运行速度，又能直接减少交通拥堵。道路收费可分为拥堵收费和排放收费。在排放收费的基础上，美国经济学家戴尔斯1968年提出了“碳排放权交易”概念，环境资源可以像商品一样交易。近年来，由碳排放权衍化而来的可交易路权(电子路票)的方法也逐渐成为缓解交通拥堵问题的研究热点。可交易电子路票可被看成是灵活的限行或者改良后的拥堵收费，不仅能缓解目前的交通拥堵问题，也有助于减轻道路拥堵收费的不公平所产生的社会和政治方面的负面影响，是一种具有较大潜力的交通策略。受环境领域中广泛应用的总量管制和交通制度的启发，YANG等[3]率先提出这种电子路票的分配和收取方案，这种方案有很多优点，在交通领域引起了广泛关注；陈慧等[4]系统介绍了可交易电子路票的基本概念和工作机制，总结了近年来研究者所得到的定性特性和理论性质；邵娟等[5]利用改进的牛顿算法对可交易电子路票作了价格设计；在可交易电子路票的实际应用中，孙振东等[6]研究了可交易电子路票下的私家车通勤路径选择，证明电子路票对出行者出行行为选择有显著的影响。另外，将可交易电子路票机制和停车换停系统组合使用，能有效改变出行需求，从而缓解交通拥堵[7]。唐杰等[8]将电子路票机制加入城市交通控制系统和诱导系统，进行协同发力，功能互补，极大地提高了交通运行效率；关艳魁[9]建立了拥堵收费和可交易电子路票机制协同多模式优化模型，并应用在了物流配送中。

与交通拥堵相伴随的是空气污染问题。统计数据表明，交通运输排放约占我国碳排放总量的10%。交通拥堵会造成车辆行驶速度过慢、通行时间增加，使车辆能耗增加，所排放的有害气体也随之增多[10]。吴亦政等[11]研究了交通环境中大气污染扩散模型，交通道路附近的大气污染严重，并持续向外扩散；袁康贵[12]分析了当下交通环境的实际影响因素，总结了影响环境的各方面要素。此外，车辆行驶速度对机动车尾气排放有着重要影响[13,14]，通过改变出行结构和行驶速度可以减少尾气排放，改善交通环境。黄琼等[15]总结并分析了国内外几种普遍应用的尾气排放模型及算法，并提出了将尾气排放模型和交通模型相结合的设想；樊杰玉等[16]通过测量不同速度和加速度下尾气排放的瞬时速率，定量分析了尾气中所含有害气体的含量，结果表明，速度对CO的排放速率均有显著影响，相关性可以用精确的排放模型来描述；张兰怡等[17]综述了国内外尾气排放模型的研究成果，分析了不同模型的优点和缺陷，并提出尾气排放和机动车所处的环境有极大的关联；WANG等[18]设计了一种能同时平衡经济增长和环境管理的交通网络设计的双目标二层规划模型。

在前期相关研究中[19，20]，笔者同时考虑尾气排放和交通系统总阻抗，构建了城市交通网络设计的多目标双层规划模型，并给出了相关数值结果。在上述相关研究中，对于上层多目标函数，其权重系数为给定的常数，这样的处理方式并不能保证得到模型的最优解，从而影响实际应用效果。为此，结合前期相关研究，对于上层多目标函数拟引进权重变量，即将上层目标函数的权重系数作为上层决策变量，该处理方式更有利于得到问题及模型的最优解。

1 符号和定义

2 多目标双层规划模型的构建

考虑通用交通网络G(N,A)，并假设出行者是同质的，即具有相同的时间价值。在可交易电子路票方案(tradable credit scheme,TCS)中引入排放函数和经济效益之后，确定上层目标函数；然后，定义弹性OD对需求情况下带有TCS的确定性用户均衡；最后，在弹性OD对需求情况下同时考虑经济效益和环境影响建立带有TCS的多目标双层规划模型。

对于一个交通网络G=(N,A)，假设每个出行者的出行时间价值相等。下面给出假设条件[1]：

1)每条路段的出行时间只是该路段自身流量的函数，与交通网络上其他路段的流量无关，也就是说不考虑路段之间的相互影响。另外，对于任意路段a的固定能力增加ya时，路段出行时间函数ta(va,ya)关于交通流量va单调递增且连续可微。

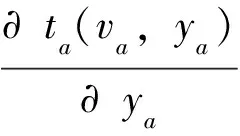
3)对于a∈A，路段能力增加的投资函数ga(ya)关于ya连续可微。

2.1 可交易电子路票方案(TCS)

笔者考虑的是基于路段的可交易电子路票收费方案，即TCS具有以下特征[2]：

1)政府将电子路票平均分配给所有出行者，不收取任何费用；

2)出行者在使用路段时需要支付该路段通行收取的电子路票，即计费方案为κ={ua,a∈A}；

3)电子路票可以根据出行者的需求在市场上自由交易，电子路票的交易价格p由市场决定，政府不干预，只起到监督的作用。

2.2 尾气排放

机动车尾气具有种类多、危害大、不易见的特点，其中主要包含CO、HC、NOx和悬浮颗粒。机动车在行驶过程中，会产生大量的CO，且CO排放量随车速的增加而减少，HC排放量和NOx排放量随车速的增加而增加。考虑到城市中一般车速都在中低速，因此选择将危害最大的CO作为排放因子进行计算。为简化分析，采用TRANSYT-7F的CO排放函数[19]：

式中：la为路段长度；ta(va)为路段出行时间。

2.3 上层模型

交通网络总的出行时间(TT)定义如下：

(1)

弹性需求下交通网络中出行者带来的总收益(TUB)定义如下：

(2)

因此，交通网络总经济效益(EB)为：

(3)

采用王炜等[3]基于平均速度对汽车的CO排放因子进行拟合所得到的最佳拟合模型(R2=0.99)：

(4)

则所考虑的交通网络CO每公里排放量为：

(5)

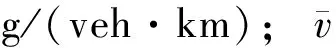
上层问题从政府角度出发，在满足投资、成本约束的条件下使交通网络的综合效益最大化(即经济效益最大化且交通排放最小化)：

(6)

路段能力增加的约束可表述为：

(7)

综上，上层问题可以表述为：

(8)

2.4 下层模型

从交通出行者角度出发，在满足弹性需求的Wardrop用户均衡(UE)条件下最小化广义出行成本(出行时间和电子路票价值的总和)。对于一个通用的交通网络G=(N,A)，存在可行的OD需求对Ωd模式和路段流模式Ωv：

(9)

(10)

因此，在给定的电子路票方案(κ,K)和道路容量扩充y∈Y下，用户均衡(UE)问题，即下层问题可以表述为：

(11)

2.5 多目标双层规划模型

弹性条件下的基于可交易电子路票机制的城市交通连续网络设计问题有2类决策者，即政府和出行者，他们具有不同的目标函数。上层问题从政府的角度考虑，在满足投资成本约束条件下最大化系统综合社会效益；下层问题从出行者的角度考虑，最小化广义出行成本，2个决策者互相牵制，并且有主从递阶的关系。因此，弹性需求条件下的基于可交易电子路票机制的城市交通连续网络设计问题的多双层规划模型(BLP)可以表示如下：

(12)

对所建立的多目标双层规划模型(12)，笔者拟将权重因子x视为上层决策者的决策变量，从而得到问题(12)的最优解。

3 模型求解

3.1 双层规划的转换

在问题(12)中，对上层目标函数引入决策者的偏好(x1,x2)可将问题(12)转化为如下双层单目标规划问题：

s.t.x1+x2=1

x1≥0,x2≥0

(13)

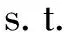
在问题(13)中，对于给定的上层决策者偏好x以及路段能力增加方案y∈S，下层规划问题满足某种约束规格下，可以得到如下下层规划问题式的K-K-T条件：

(14)

(15)

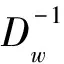
(16)

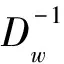
(17)

(18)

(19)

(20)

(21)

式中：ρw，p以及μw为下层问题相应约束条件的拉格朗日乘子；μw表示OD对w的广义出行成本；p表示电子路票在市场中的单位交易价格。

因此，在问题(13)中，以下层规划问题的K-K-T条件代替下层问题，则问题(13)可以转化为如下的一般非线性规划问题：

(22)

3.2 松弛算法

对于问题(22)，由于互补约束条件的存在，光滑优化问题的约束规格得不到满足，直接采用一般的非线性规划方法求解问题(22)比较困难。因此，笔者拟采用文献[1]和[18]中设计的松弛算法对问题(22)进行求解。松弛算法的主要思想是对互补条件(14)、(16)、(18)、(20)进行近似化处理，主要求解步骤如下：

步骤1 设置辅助参数初始值：θ0>0，ε>0，更新因子λ∈(0,1)，迭代次数k=0。

步骤2 将互补条件(14)、(16)、(18)、(20)分别设置辅助参数θk，并求解如下松弛的单层非线性规划问题：

s.t.x1+x2=1,0≤x1,x2≤1

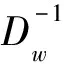
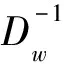
(23)

并得到最优解(yk,vk,uk,dk,μk,ρk,pk,xk)。

步骤3 若θk<ε，停止计算并转步骤4；否则令θk+1=λθk，转到步骤2。

步骤4 得到最优解(y*,v*,d*)=(yk,vk,dk)。

4 模型有效性

采用美国公共道路局1964年公布的路段出行函数：

(24)

式中：Ta和ba是参数，分别表示路段a的自由通行时间和原始通行能力。

考虑到增加了路段通行能力ya和电子路票pua，所以路段出行函数可以表示为：

(25)

对于路段a增加的容量ya，道路改造建设所需的成本函数记为：

(26)

为了验证模型(13)的有效性，笔者采用与文献[19]相同的交通网络模型，即图1所示的交通网络，车辆从A、B两地出发到达C地，网络有5个节点包括2个起节点和1个讫节点，5条路段和2个OD对：AC和BC，对5个路段进行改造，扩大路段容量ya并收取电子路票，出行者使用路段所需电子路票数量分为ua，投资预算B=1000，分配给OD对w上每个出行者的电子路票数量qw=5，φ=0.1和其他相关数据如表1所示。

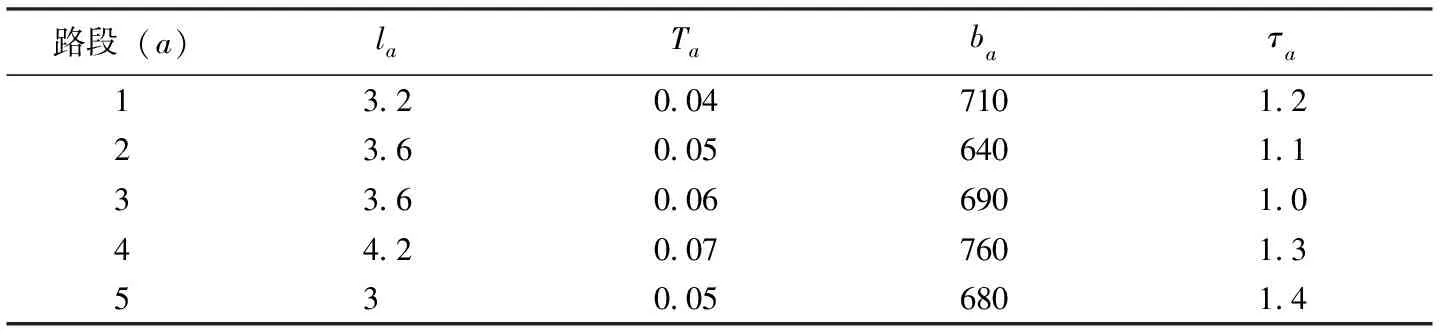
表1 交通网络相关参数

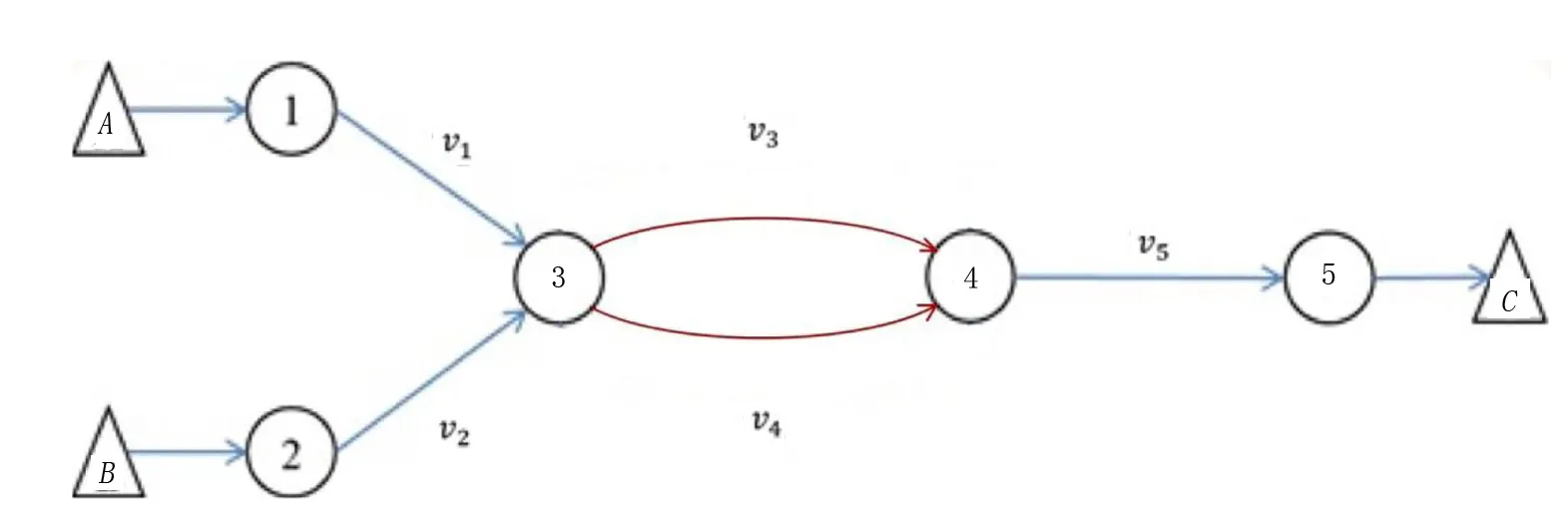
图1 交通网络模型

利用模型(13)对图1的交通网络进行求解，得到该交通网络中道路总阻抗和CO尾气排放量的综合效益为-2199.690，其他数据见表2。

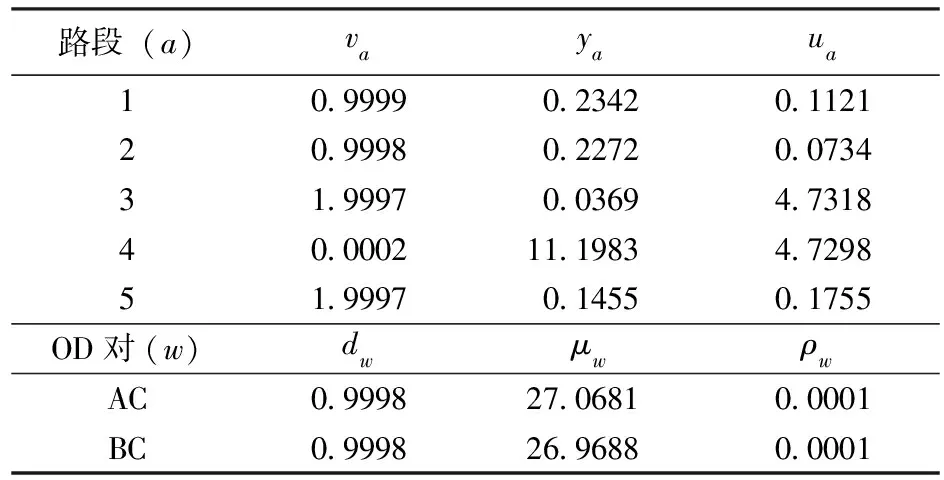
表2 模型(13)所得到的最优解

表3给出了模型(13)得到的上述交通网络中道路总阻抗和CO排放量与前期相关研究工作得到的数值的比较，不难看出，笔者所建立的模型能够获得更优的综合效益。这也表明了笔者所建模型的可行、有效性。

表3 结果比较

值得指出的是，相比于前期研究工作，将上层权重系数作为整个模型的变量，更加有利于从整体的角度对权重变量进行优化，而不是仅仅将上层权重系数给定为某个固定的值。当然，在该模型中，最优权重为x=(1,0)，相当于没有考虑上层第2个目标，这主要是由于2个目标函数的数量级相差比较大。

5 结语

在综合考虑交通网络总阻抗和尾气排放的基础上，构建了弹性需求下带有可交易电子路票的交通网络多目标双层规划模型。为得到模型的最优解，将上层多目标函数引入权重变量，通过对权重变量的优化得到问题的最优解。数值结果表明，相比于前期相关工作，笔者构建的模型更能得到最优的综合效益。