基于深度卷积神经网络的复杂多目标规划问题机器学习方法
2022-05-21张涛陈薇周俊刘瑞林陈芳
张涛,陈薇,周俊,刘瑞林,陈芳
长江大学信息与数学学院,湖北 荆州 434023
多目标规划问题是指同时优化多个相互冲突目标的优化问题,由于其可以全面体现决策者的意愿,从而广泛应用于工程实践中,如跨流域调水问题[1]、土地资源使用问题[2]、工程设计问题[3]、绿色煤炭生产问题[4]等。但由于多目标问题的复杂性,其有效的算法设计一直是优化领域的研究热点。
智能算法的发展促进了最优化方法从“方法定向”到“问题定向”的转变。相对于传统算法,智能优化算法具有以下优点:对目标函数和约束函数的性能要求更为宽松;计算效率比理论上的最优性更为重要;多数算法有一个多个体的种群,寻优过程实际上就是一个种群进化的过程。结合多目标规划问题的结构特征,智能算法已成为求解多目标规划问题的重要手段。SCHAFFER设计了求解多目标规划问题的向量评价遗传算法(VEGA)[5];FONSECA和FLEMING提出了求解多目标规划问题的遗传算法MOGA[6],该算法易于操作且计算效率较高,但该算法过于依赖共享参数,极易陷入局优;SRINIVAS和DEB提出了求解多目标规划问题的非受控排序遗传算法(NSGA),该算法具有较好的收敛性且Pareto最优解分布均匀,但算法计算量大,计算复杂度高[7];HORN等提出了基于小生境技术的多目标规划问题的遗传算法(NPGA),该算法计算效率较高且能获得较好的Pareto最优解集,但难以选择和调整小生境半径和比较集的规模[8];KNOWLES等提出了基于外部存档的多目标进化算法(PAES),该算法利用外部存档技术保留非支配个体,并采用一种自适应的网格保持种群的多样性[9];CORNE等利用挤压系数保持种群的多样性,提出了Paeto包络的多目标优化选择算法(PESA)[10];后续又对PESA 算法进行改进,提出了求解多目标规划问题的PESA-Ⅱ算法,该算法采用网格选择,与基于个体选择的PESA算法相比,在一定程度上提高了算法的运行效率[11];基于外部精英集存档技术和保持种群多样性的聚类技术,结合基于个体强度的适应度赋值方法,ZITZLER等提出了求解多目标规划问题的强度Pareto进化算法(SPEA),该算法为多目标进化算法的设计提供了一种新的思想,但该算法在选择压力较小时,几乎等效于随机搜索[12];他们后续又对SPEA算法的适应度分配策略、个体分布性评估方法以及非支配解集的更新策略进行了改进,提出了第二代求解多目标规划问题的强度Pareto进化算法(NSGA-Ⅱ),该算法虽然与SPEA算法的计算复杂度相同,但SPEA-Ⅱ的Pareto最优解的分布均匀性得到了极大的提高[13];基于快速非受控技术,DEB等提出了求解多目标规划问题的快速非受控排序遗传算法(NSGA-Ⅱ),该算法具有良好的收敛性与Pareto最优解具有较好的分布均匀性且计算效率较高,但难以找到孤立点[14]。
自2003年开始,由于粒子群优化算法以及人工免疫系统优化算法等新的进化思想被引入多目标优化的领域,多目标进化算法的研究又得到了进一步的发展。2004年,COELLO等提出了多目标规划问题的粒子群算法(MOPSO),该方法简单易行且具有较高的计算效率[15];2008年,基于人工免疫系统模拟抗体的优化过程,JIAO等提出了经典的求解多目标规划问题的非支配邻域免疫算法(NNIA),该算法收敛速度较快,在求解高维多目标优化问题时具有一定的优势[16]。
近年来,国内外学者以多目标进化算法为主要手段,设计了一系列的多目标规划问题求解算法,并取得了一定的成果。然而,多目标规划问题进化算法中仍存在一些共性问题:测试函数的Pareto最优解集模式单一;种群多样性与算法收敛速度相互牵制,且随着问题维度的增加,求解难度急剧上升。最近,深度卷积神经网络因在图像边缘提取中的高效性备受瞩目,该方法几乎可以“瞬时”完成图像边缘提取。事实上,将多目标规划问题的像空间进行图像表征,则Pareto最优前沿通常映射为图像边缘的特定部分。基于此,笔者设计了一种基于深度卷积神经网络的复杂多目标规划问题的机器学习方法。
1 模型与基本概念
假设x∈Rn,f:Rn→Rm,g:Rn→Rq,以最小化问题为例,多目标规划问题的数学模型可表述为:
(1)
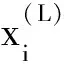
多目标规划问题的概念图如图1,相关定义如下:
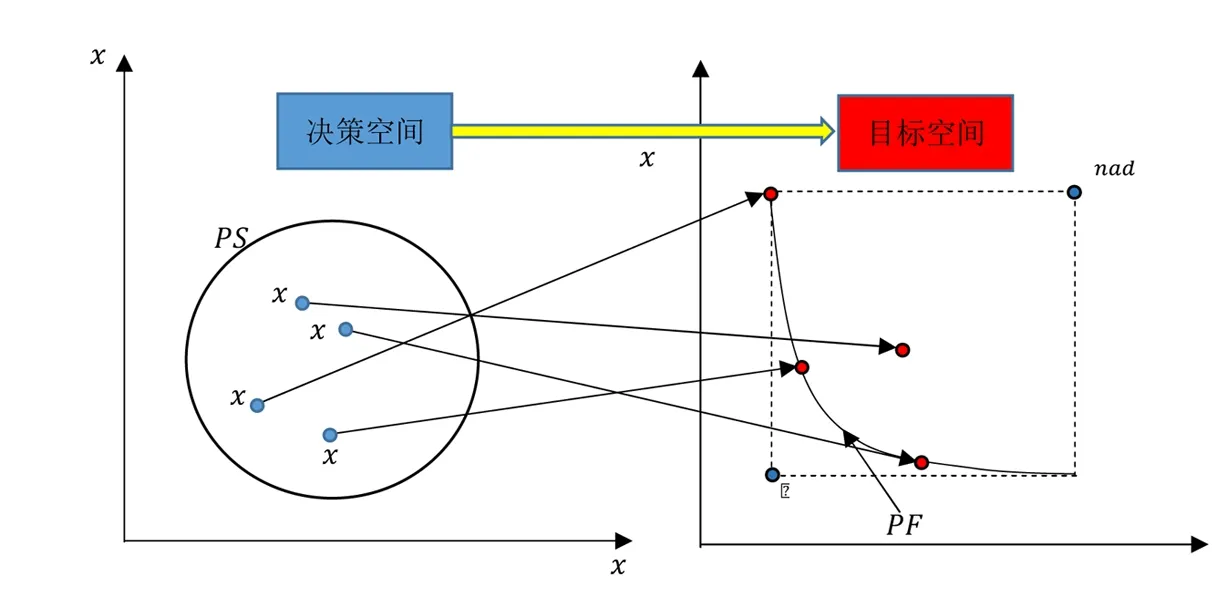
图1 多目标规划概念图
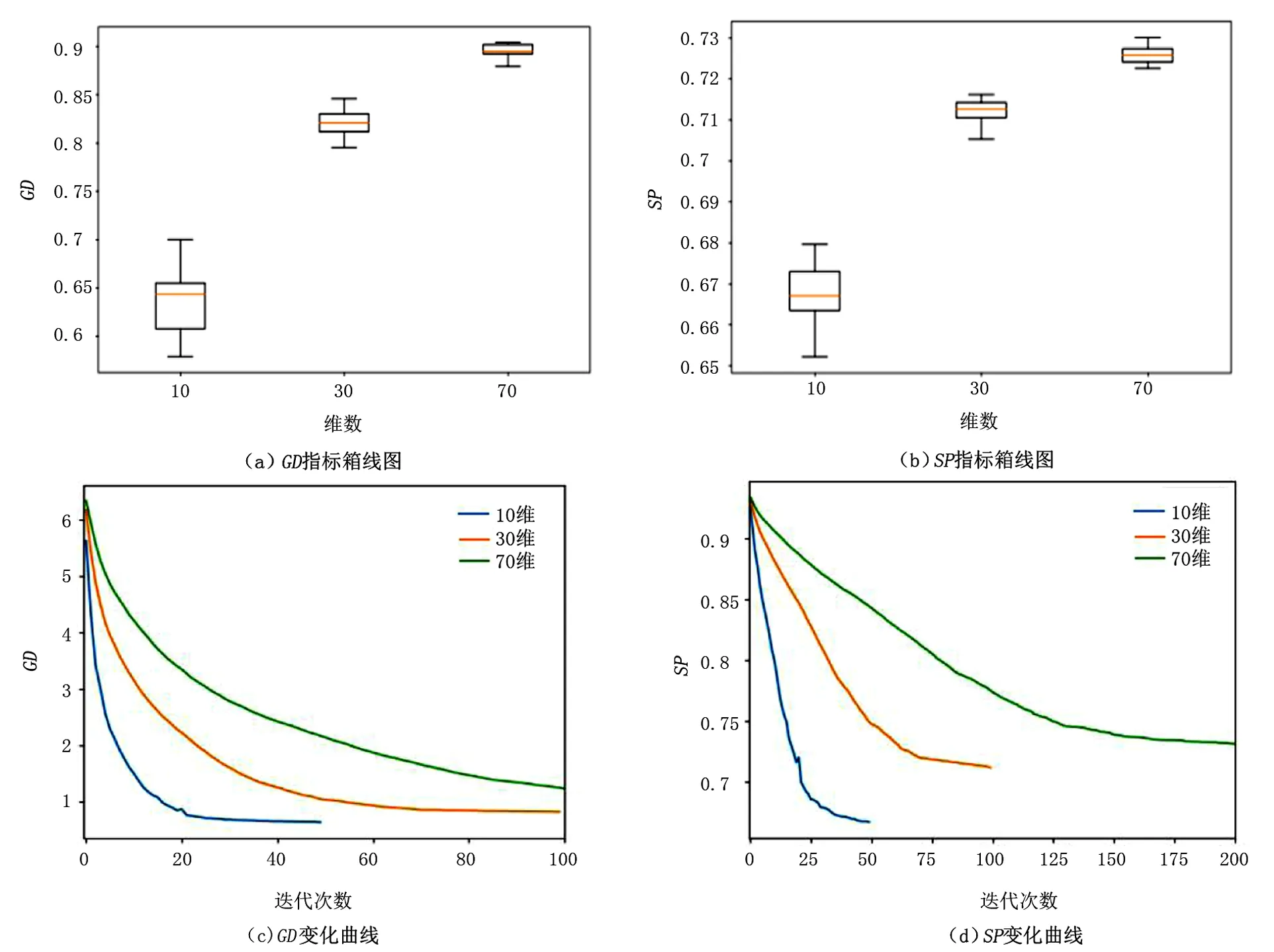
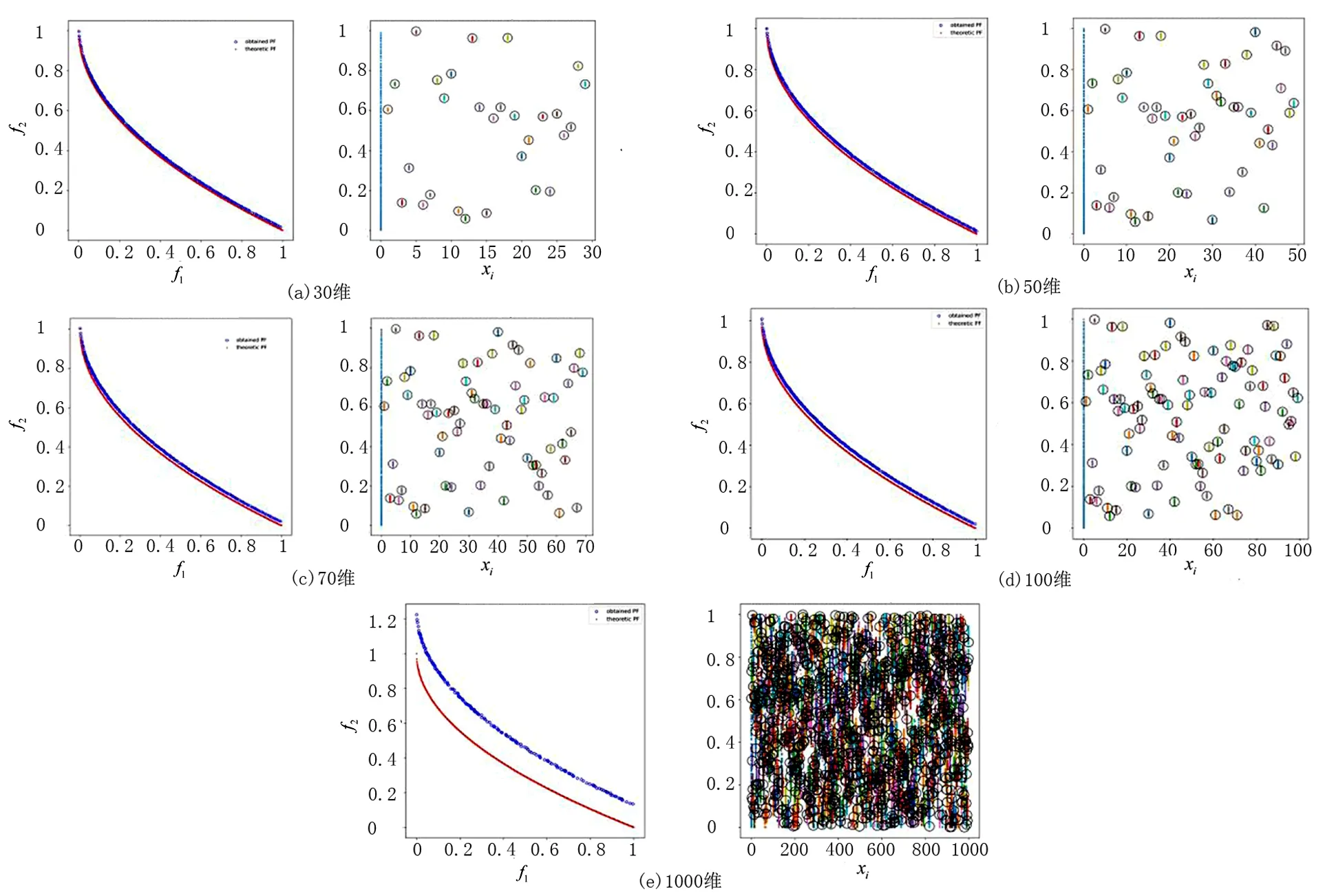
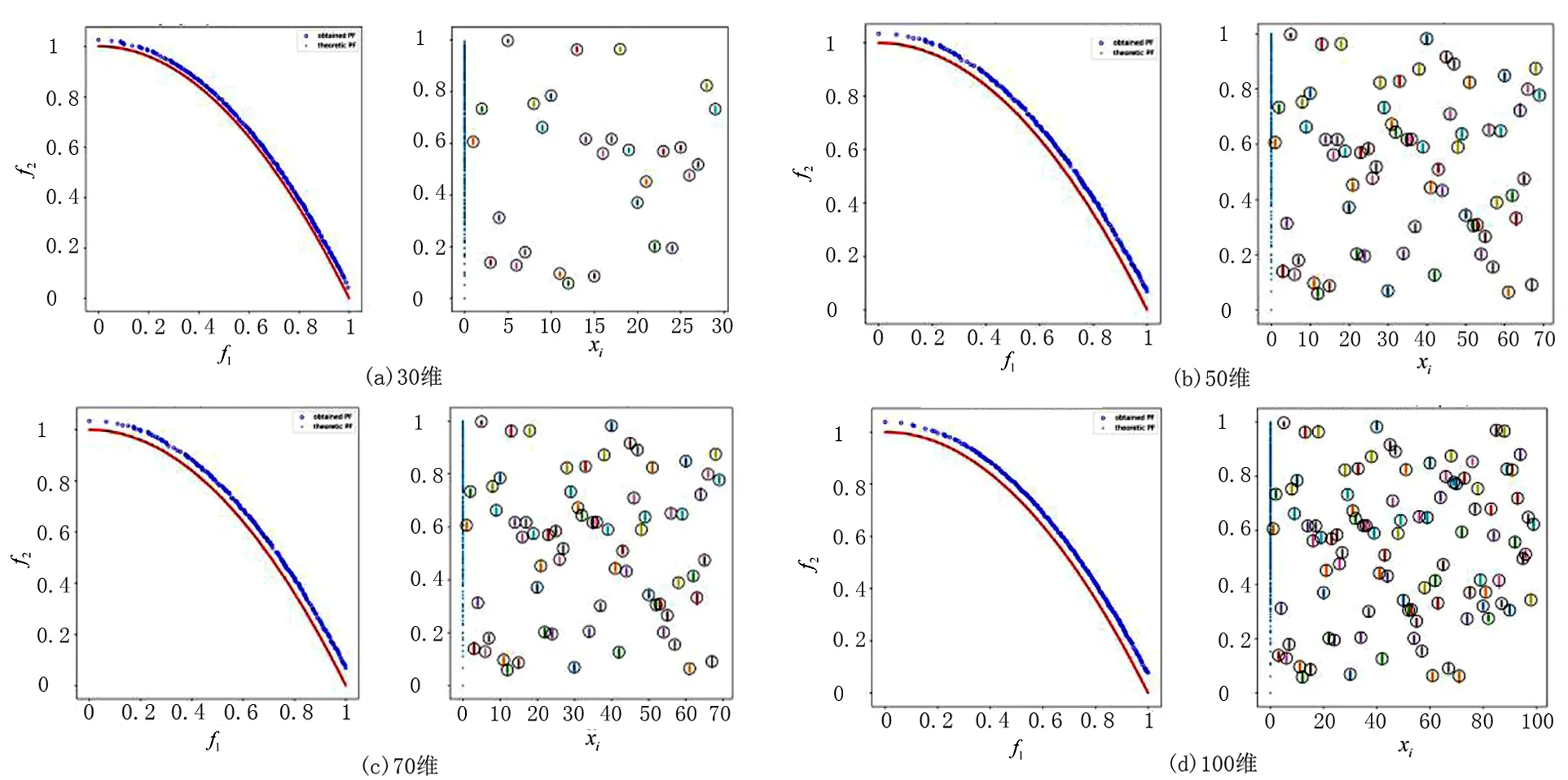
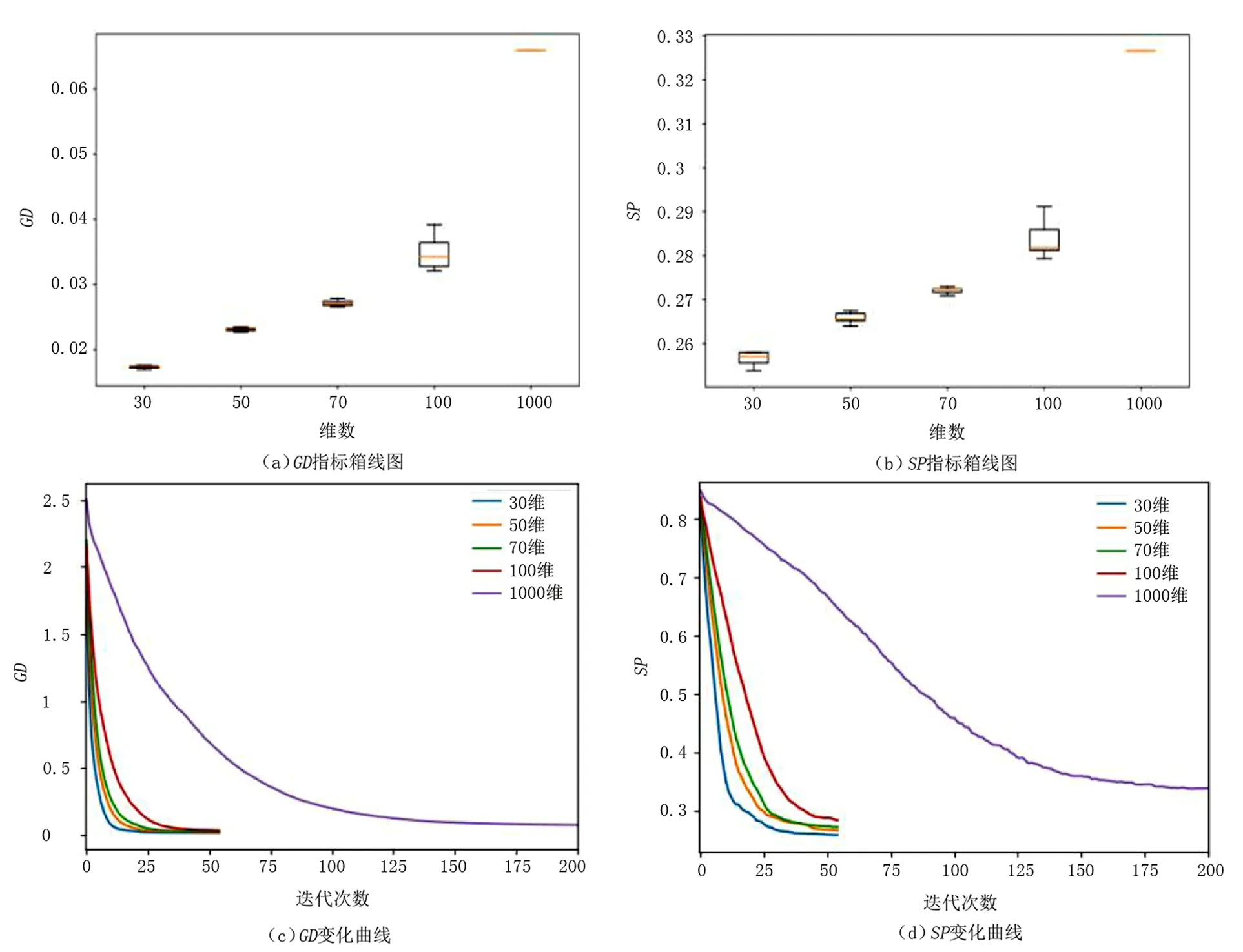
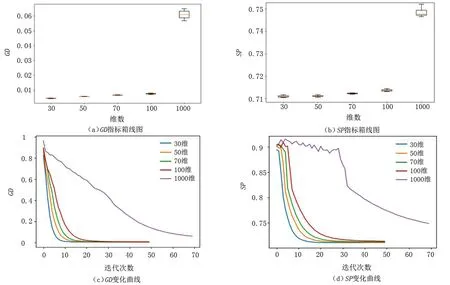
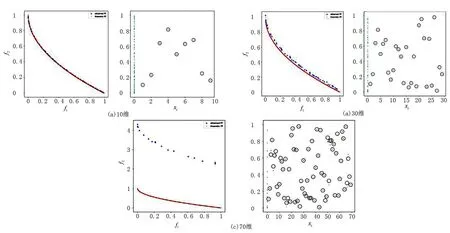
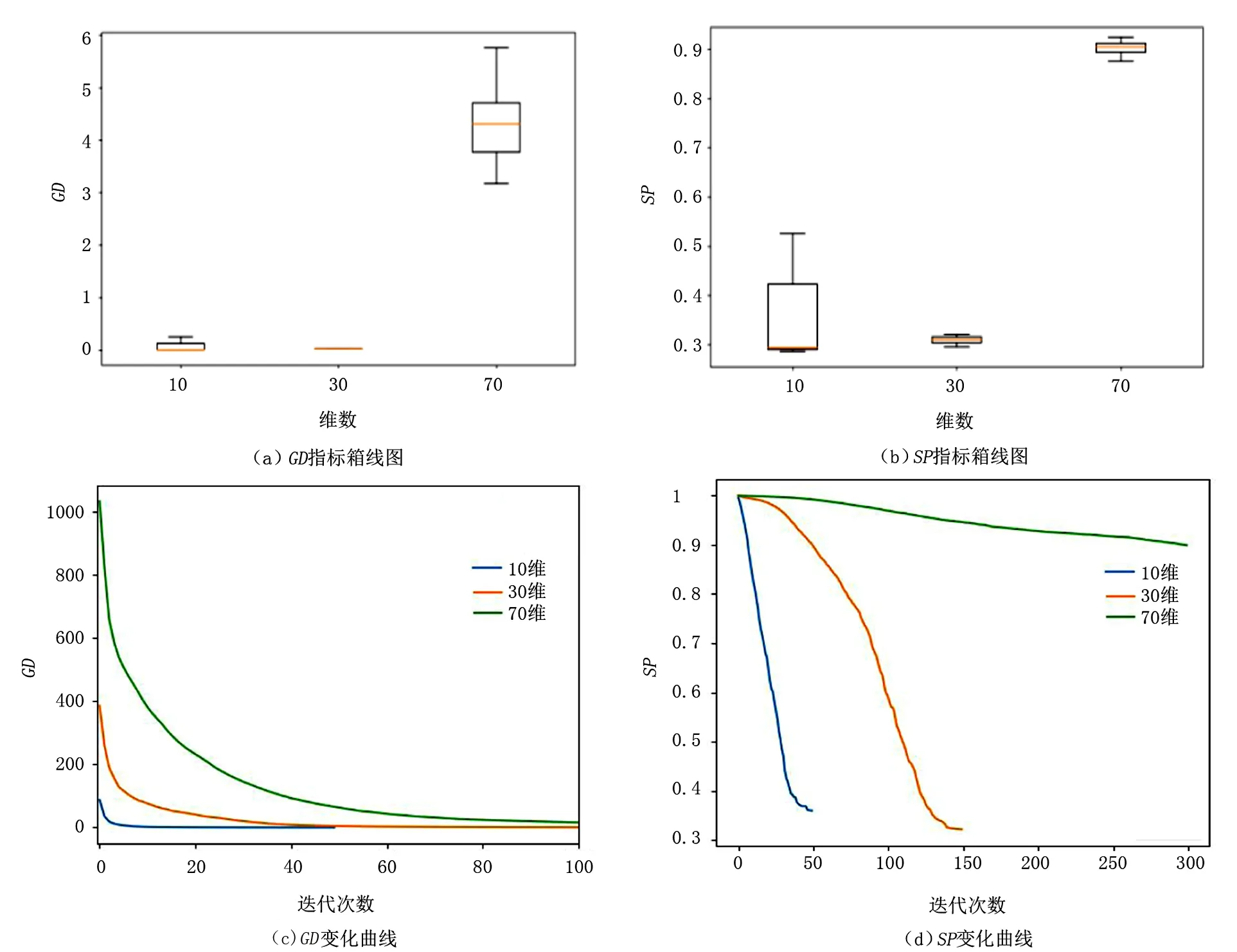
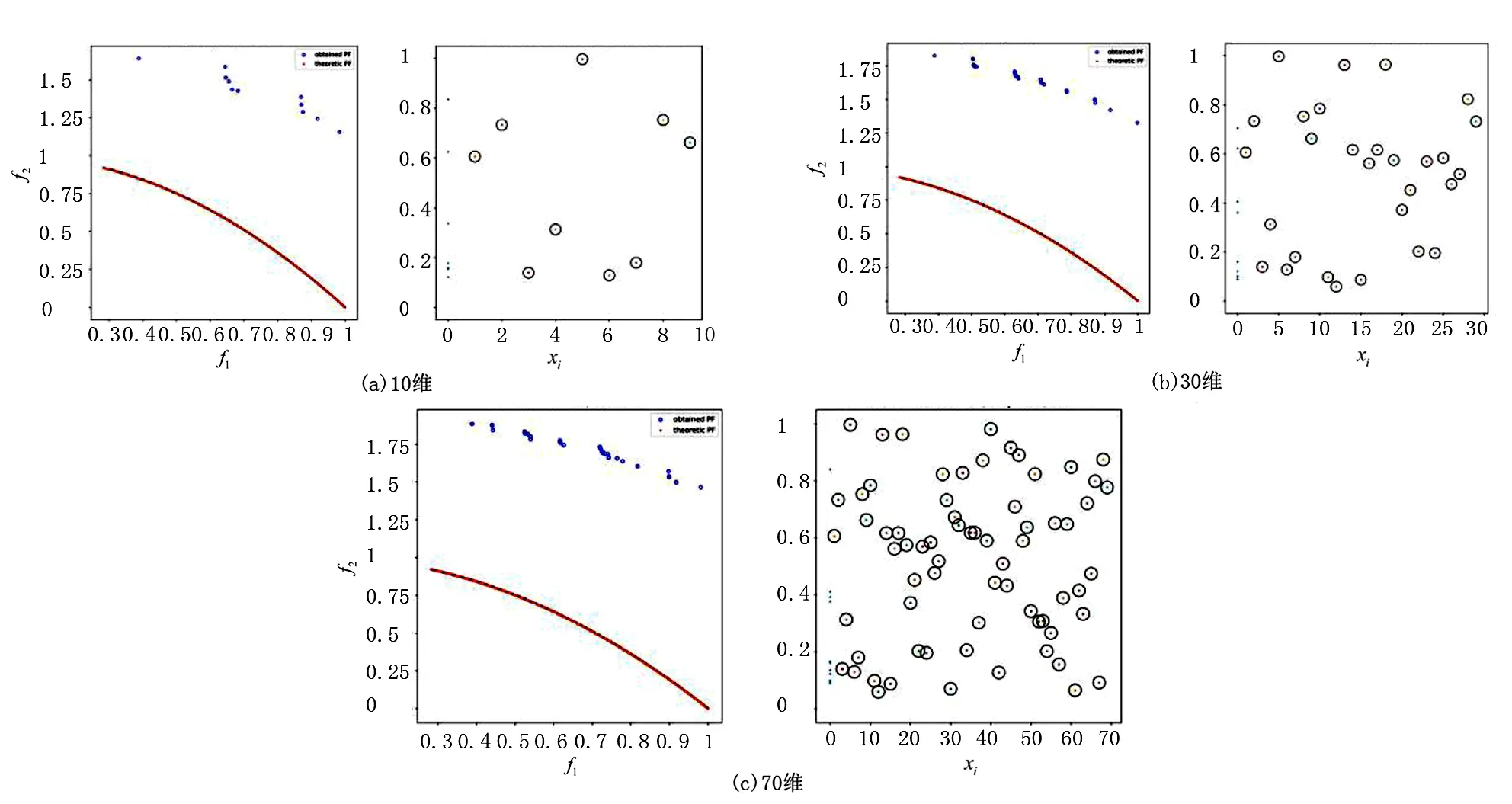
定义1(Pareto支配)对任意2个可行解x和y,若对∀i∈{1,2,…,m}满足fi(x)≤fi(y),且∃i∈{1,2,…,m},使fi(x) 定义2(Pareto最优解)对可行解x*,若不存在x∈S,使得xx*,则x*为问题(1)的一个Pareto最优解。 定义3(Pareto最优解集)给定问题的所有Pareto最优解构成Pareto最优解集(Pareto-optimal set,PS),记作: P*={x*∈S|∃x∈S,x*x} 定义4(Pareto前沿)对于给定问题的所有Pareto最优解所对应的目标向量构成问题(1)的Pareto前沿(Pareto Front,PF),记作: PF*={f(x)=(f1(x),f2(x),…,fm(x))|x∈P} s.t.x∈Ω 首先,在原像空间中,提出“部分精英集的Gauss采样+部分拉丁超立方采样”的混合采样新方法,其中部分样本以精英集中的Pareto最优解为中心进行Gauss采样以保证所获Pareto前沿不差于上一代,部分样本利用拉丁超立方采样以保证样本的多样性。接着,在像空间中,利用基于深度卷积神经网络图像特定边缘提取直接获取Pareto最优前沿。反复迭代上述过程,直到满足精度要求。 算法流程如下所述: Step 1 在决策空间中随机初始化一组解X,设置循环次数N; Step 2 将X带入问题模型得到Y; Step 3 利用深度卷积神经网络从Y构成的图像中提取Pareto最优前沿Z; Step 4 得到Pareto前沿Z对应的决策变量集合S; Step 5 由S根据智能采样算法产生新的决策变量集合X; Step 6 从Step 2开始循环N-1次。 智能采样算法流程如下: Step 1 得到当前最优解集S; Step 2 以S中每个向量为中心,进行Gauss采样得到集合P; Step 3 生成一组随机数组成集合R; Step 4 将S、P和R合并后进行拉丁超立方采样,得到集合Q; Step 5 将S、P和Q合并,得到新的样本集合X。 基于深度卷积神经网络的Pareto前沿提取算法流程如下: 步骤1 将目标空间图像转换成二值数字图像; 步骤2 根据图像大小,设置相应的卷积核,建立深度卷积神经网络模型,其中卷积核设置如下: 网络所需层数由卷积核大小和输入图像大小计算后设置; 步骤3 将数字图像输入神经网络模型得到对应的Pareto前沿图像; 步骤4 将Pareto前沿图像转换成对应的Pareto解集。 为了测试算法求解复杂多目标规划问题的效率和普适性,基于文献[14],将5个经典多目标规划问题进行了如下改进:①重新构造测试模型,测试模型的最优Pareto解集具有随机性;②增加测试模型维度。改进后的测试模型称为R-ZDT。所有试验均在Dell Precision 7530移动工作站上运行,工作站主要配置如下:Nvidia Quadro P3200M(6GB RAM,1792 CUDA core)的GPU、Intel i7-8750H CPU以及16GB RAM。 改进后的测试模型R-ZDT1~R-ZDT5分别如下: R-ZDT1: R-ZDT2: R-ZDT3: R-ZDT4: R-ZDT5: 其中:xi∈[0,1];εi~U([0,1])。 算法的性能评价主要分为2个方面:一是衡量算法收敛性能的指标,刻画利用算法所得最优解和理论Pareto最优前沿的逼近程度,如世代距离指标GD;二是衡量算法多样性的指标,主要衡量解集在PF上分布的均匀程度,如空间指标SP。 世代距离指标GD计算公式如下: (2) 式中:np=|P|;m为目标个数;di表示为P中第i个解到P*上离其最近的解的欧式距离。GD的值越小,算法的收敛性能越好。一般地,P*由问题的真实PF上均匀采样的点集构成。 空间指标SP计算公式如下: (3) 改进测试模型R-ZDT1~R-ZDT5的求解结果分别如图2~图11所示。图2、4、6、8、10中,各分图的左图展示问题的理论Pareto最优前沿与利用笔者算法求解得到的Pareto最优前沿,右图展示理论Pareto最优解集与利用笔者算法求解得到的Pareto最优解集。 图11 R-ZDT5的GD和SP指标箱线图及变化曲线 值得注意的是,所有测试函数的最优前沿均与模型中的f2(x)函数密切相关。其中,测试函数R-ZDT1~R-ZDT3中的f2(x)函数为单调函数,测试函数R-ZDT4和R-ZDT5中的f2(x)函数具有多模态性。对于测试模型R-ZDT1~R-ZDT3,从图2、图4以及图6可以看出,利用笔者算法所获得最优Pareto前沿面能很好地收敛到理论最优Pareto前沿面且分布均匀;从图3、图5以及图7可以看出,算法在保证收敛的前提下具有较快的收敛速度。 图2 R-ZDT1的Pareto最优前沿和Pareto最优解集 图3 R-ZDT1的GD和SP指标箱线图及变化曲线 图4 R-ZDT2的Pareto最优前沿和Pareto最优解集 图5 R-ZDT2的GD和SP指标箱线图及变化曲线 图6 R-ZDT3的Pareto最优前沿和Pareto最优解集 图7 R-ZDT3的GD和SP指标箱线图及变化曲线 对于测试函数R-ZDT4,由于f2(x)函数的多模态性,导致原问题具有多个局部Pareto最优前沿,算法极易陷入局优。从图8可以看出,当决策变量维数小于70时,利用笔者算法所获得最优Pareto前沿面能很好地收敛到理论最优Pareto前沿面且分布均匀;从图9可以看出,该算法具有较快的收敛速度。 图8 R-ZDT4的Pareto最优前沿和Pareto最优解集 图9 R-ZDT4的GD和SP指标箱线图及变化曲线 对于测试函数R-ZDT5,从图10和图11可以看出,算法虽然具有较快的收敛速度但全局收敛性较欠缺。 图10 R-ZDT5的Pareto最优前沿和Pareto最优解集 针对多目标规划进化算法中测试函数的Pareto最优解集模式单一、种群多样性与算法收敛速度相互牵制的问题,提出了一种基于智能采样和特定边缘提取的多目标规划问题算法。其中,智能采样中的高斯采样用于局部搜索,超立方拉丁采样用于全局搜索,利用卷积神经网络特定边缘提取实现最优Pareto最优前沿的“瞬间”提取。最后,对5个复杂多目标规划问题进行仿真试验,结果表明,该算法对求解复杂多目标规划问题的具有可行性且具有较高的计算效率。未来,还需要深入挖掘该算法的采样机理,对算法进行改进,并从理论上明确该算法的最佳应用范围;对于具体的边缘提取,根据其原理,进一步简化网络架构。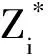

2 算法
2.1 算法总体流程
2.2 智能采样算法流程
2.3 基于深度卷积神经网络的Pareto前沿提取算法
3 数值试验与结果分析
3.1 测试模型
3.2 算法性能评价指标
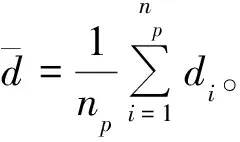
3.3 试验结果


4 结语
