金属靶板侵彻数值模拟对比研究*

陈 亚，谈 超，郭亚洲,3

（1. 西北工业大学航空学院，陕西 西安 710072；2. 西安现代控制技术研究所，陕西 西安 710072；3. 西北工业大学冲击动力学及工程应用陕西省重点实验室，陕西 西安 710072）

数值模拟已成为当今科学研究的重要手段，而有限元软件作为数值模拟的具体实现途径，也成为探究科学和工程问题不可或缺的工具。将数值模拟与实验相结合，不仅可极大降低研究成本，完善实验中不易测得的物理量，同时也可以为理论研究提供数据支撑。在金属靶板侵彻这一问题上，利用数值模拟技术已进行了大量研究。

Rusinek 等使用ABAQUS 对弹体侵彻进行了数值模拟，靶板材料为钢，型号为Weldox 460E，厚度为12 mm；弹体为圆锥形，弹体速度为120～600 m/s；选用Johnson-Cook (J-C)本构模型和J-C 失效准则，探究了弹体直径对靶板穿透效果的影响。结果表明，弹道极限与弹体直径呈线性关系，侵彻过程中靶板温升与设置的摩擦因数有关，摩擦因数越大，靶板温升越大。Iqbal 等借助ABAQUS 软件，针对靶板材料1100-H12，并分别设置1 mm 厚的单层和双层（0.5 mm+0.5 mm） 2 种靶板，选用J-C 本构模型和失效准则，探究了这2 种靶板所表现出来的抗侵彻差异。模拟结果表明，单层靶抗卵形弹体侵彻性能优于双层靶。Børvik 等采用LS-DYNA 开展了不同形状（平头形、半球形和圆锥形）弹体侵彻模拟工作，靶板与Rusinek 等的研究对象相同，仍然选用J-C 本构模型和失效准则，数值模拟结果与实验结果吻合较好。Dey 等在Børvik 等模拟结果的基础上，利用LS-DYNA 进行了侵彻模拟来探究最准确的失效准则，结果发现带损伤的J-C 本构和失效准则效果最佳，模拟数据与实验数据吻合最好。Flores-Johnson 等选取铝板和钢板，型号分别为7075-T651 和Weldox 700E，弹体为圆锥形，同样选用J-C 本构模型和失效准则，利用LS-DYNA 探究靶板层数对抗侵彻能力的影响，模拟结果表明，相同材料和厚度的多层靶抗侵彻性能远低于单层靶。

当前比较常用的可用于模拟侵彻问题的数值软件包括LS-DYNA、ABAQUS、PAM-CRASH、NASTRAN、MARC、MAGSOFT、ADINA 和COSMOS 等。每种软件都有其自身特点，无法简单评价哪种软件最强大。但是在具体的工程实践中，能正确地选择合适的软件是模拟成功的重要因素。本文中，将以文献[4-5, 9-12]的相关侵彻实验为基础，结合J-C 本构模型和失效准则，利用CATIA 建模，采用HYPER-MESH 进行网格划分，采用LS-DYNA、ABAQUS、PAM-CRASH 等3 种软件进行模拟分析，并对这3 种软件的模拟能力进行整体的比较与分析，通过综合比较其弹体剩余速度、弹体变形量、靶板变形量以及冲塞块速度等物理量的模拟结果与实验结果的差异，分析不同软件的优缺点，为靶板侵彻问题模拟工具的合理选择提供依据。

1 计算模型和方法

1.1 实验数据与结果来源

本文中主要采用数值模拟手段对不同商业软件进行对比研究，因此实验方案与设计均来自文献[9-12]。在其实验中，靶板材料为钢，型号为Weldox 460E，边长为500 mm，厚度为12 mm；弹体由ARNE 工具钢制成，直径（20 mm）和质量（197 g）是恒定的，由于质量恒定，弹体的长径比（/）比有所变化，不同弹体的几何形状如图1所示。

图1 实验中所使用的弹体[11]Fig. 1 Projectiles used in the experiments[11]

平头形弹体侵彻实验中选取10 种不同初始冲击速度，分别为399.6、303.5、285.4、244.2、224.7、200.4、189.6、184.3、184.8 和181.5 m/s。半球形弹体侵彻实验中选取7 种不同初始冲击速度，分别为452.0、420.6、362.9、326.7、300、292.1 和278.9 m/s。需要说明的是，本文中所述的初始速度即为弹体的着靶速度。根据测得的弹体初始速度和残余速度，可以绘制残余速度曲线，如图2所示。弹道极限速度定义为最高冲击速度（未打穿）和最低冲击速度（目标完全打穿）之间的平均值。

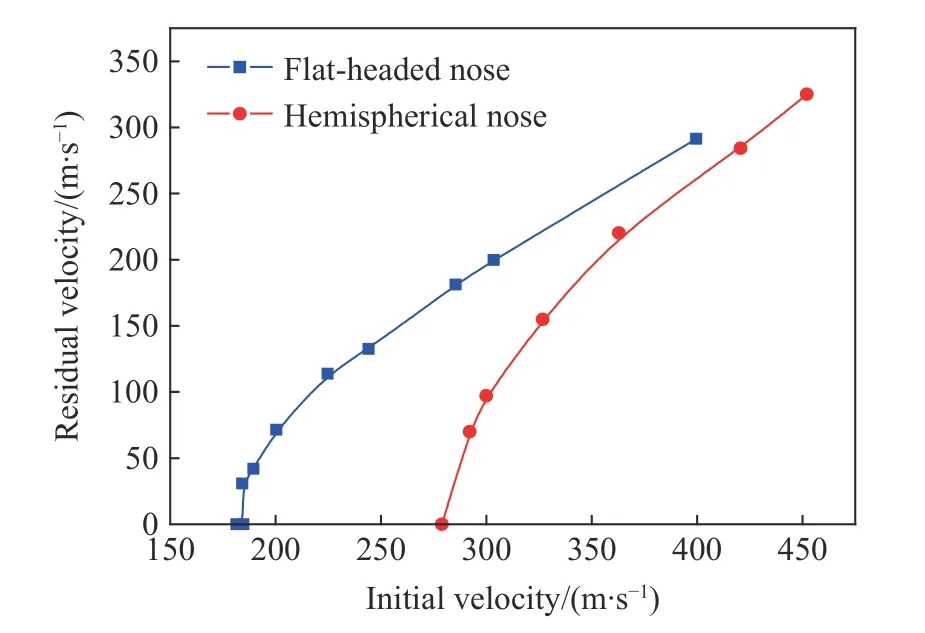
图2 不同形状弹体侵彻钢板时，弹体剩余速度随弹体初速度的变化[11]Fig. 2 Changes of projectile residual velocities with their initial velocities during penetration of the projectiles with different nose shapes into steel targets[11]

从图2中的剩余速度曲线可以得出一些直接结论。首先，可以看出弹体头部的形状会明显影响靶板的弹道阻力。半球形弹体的弹道极限速度近300 m/s，而平头形弹体的弹道极限速度低至185 m/s。观察到的弹道极限速度的差异主要归因于弹体形状引起的破坏模式的变化。平头形弹体在侵彻过程中，会有近似圆形的冲塞块从靶板中弹出，这种破坏模式主要由剪切带决定。半球形弹体侵彻时，则主要是通过延性孔扩大而穿透目标，将弹体前面的材料推开，经过剧烈的局部鼓胀后，半球形弹体从靶板中冲击出杯状冲塞块。

1.2 计算模型

本文中为保证不同有限元软件模型的统一性，所有模型在CATIA 中统一建模，采用HYPERMESH 划分网格，如图3 所示。并采用自定义单位制，长度单位为mm，时间单位为s，质量单位为g。其他单位可由这些基本单位推导得来。

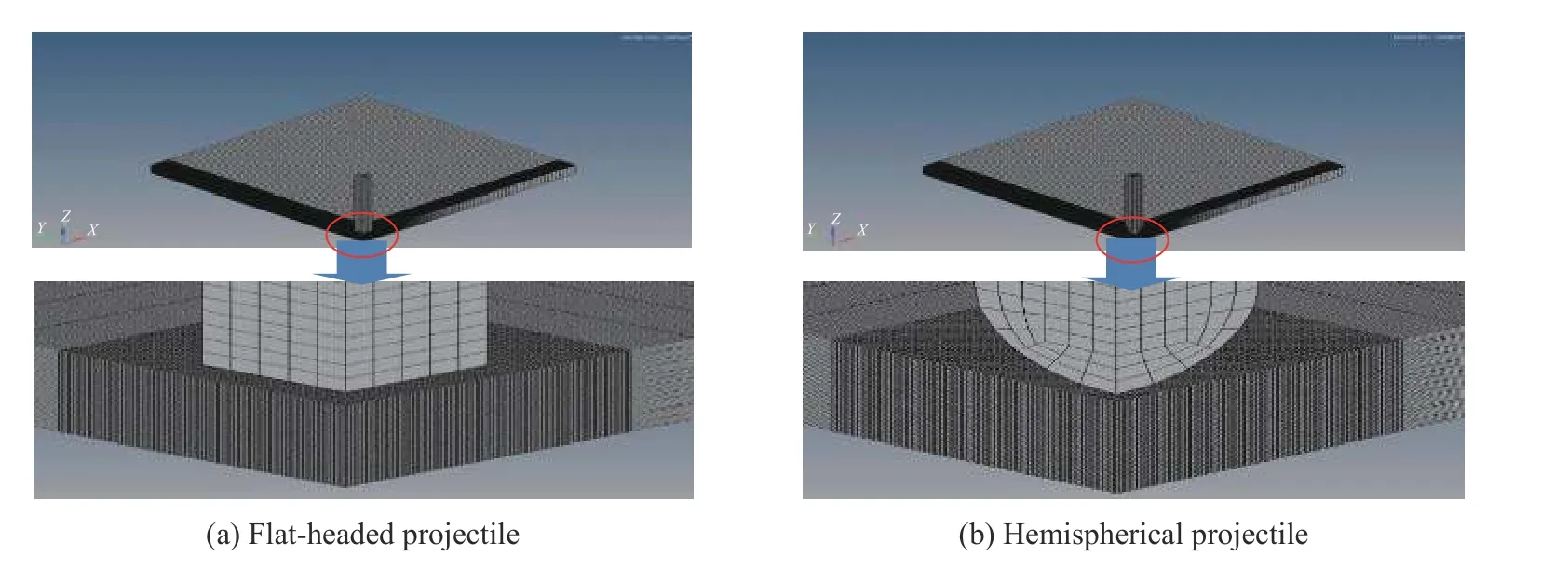
图3 弹体和靶板有限元模型Fig. 3 Finite element models of the projectiles and targets

鉴于PAM-CRASH 主要为三维碰撞模拟软件，此次建模均为三维模型。但为尽量减小计算工作量，考虑到模型的对称性，将数值分析的模型取整个模型的1/4。网格划分时，弹体与靶板接触区域网格加密，最密处网格单元尺寸为0.2 mm，远离接触的区域逐渐过渡为稀疏的网格。

1.3 材料模型

2 计算结果对比分析

2.1 平均相对误差

在有限元模拟中，误差是模拟结果与真实值之差。结合误差定义，此次通过计算多组实验数据与模拟数据相对误差的平均值来探究模拟结果的优劣：

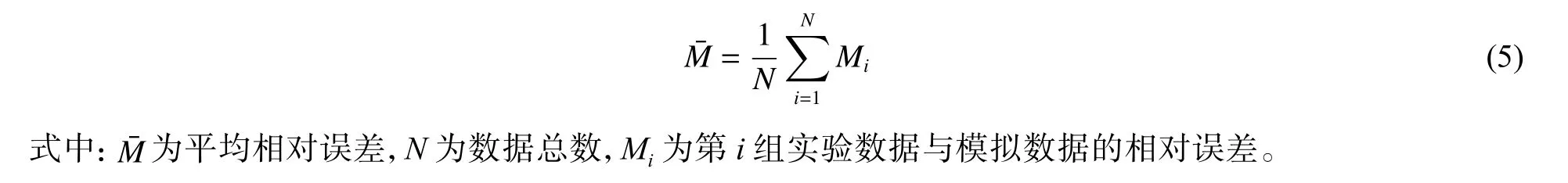
2.2 失效模式对比分析

图4～5 所示为使用3 种有限元软件对平头形弹体和半球形弹体侵彻12 mm 厚钢板过程的模拟结果，靶板材料为Weldox 460E（PAMCRASH 无法取镜面对称，保留1/4 模型）。模拟结果与实验结果分析的破坏模式十分类似。通过图4 可以清楚地发现，在3 种软件的模拟结果中，平头形弹体产生的破坏都是冲塞破坏，一个近似靶板厚度的冲塞块被挤压出来。在25 和50 µs 时，即弹体接触上靶板且冲塞块还未脱离靶板时，弹体与靶板的接触面应力最高，ABAQUS 和PAM-CRASH 的模拟结果约为3×10Pa，LSDYNA 的模拟结果约为1×10Pa。而在75 µs 后，冲塞块从靶板中打出，此时靶板冲塞孔处的应力最高，ABAQUS 和PAM-CRASH 模拟结果约为6×10Pa，LS-DYNA 模拟结果约为1.1×10Pa。而图5 展示的半球形弹体侵彻模拟结果表明，弹体将靶板挤向弹头的两侧，碰撞区域靶板不断变薄。同时弹体前进的速度导致该区域出现了强烈的拉伸应变，将一个薄塞块从靶板中挤出。结合3 种软件模拟的应力云图可发现，每时每刻应力最高区域均为弹体与靶板的接触面，应力约为1.2×10Pa。

图4 模拟得到的平头形弹体在224.0 m/s 速度下侵彻过程中的von Mises 应力云图Fig. 4 Simulated von Mises stress contours for penetration of the blunt flat-headed projectile with the initial velocity of 224.0 m/s

图5 模拟得到的半球形弹体在327.0 m/s 速度下侵彻过程中的von Mises 应力云图Fig. 5 Simulated von Mises stress contours for penetration of the hemispherical projectile with the initial velocity of 327.0 m/s

2.3 弹体参数模拟结果对比分析

弹体剩余速度是衡量有限元软件侵彻模拟效果最直接的参数。图6 为不同有限元软件弹体剩余速度的模拟结果与实验结果的对比。从图6 可以看出，3 种软件模拟结果与实验结果大体上吻合，所呈现的曲线变化趋势也几乎一致。在差异方面，平头形弹体侵彻模拟效果稍好于半球形弹体模拟；半球形弹体模拟效果最好的是初速度在高于弹道极限100 m/s 左右时；而在平头形弹体模拟中，除LS-DYNA 误差较大外，另2 种软件的模拟结果与实验结果均基本吻合。此外，2 种弹体形状的侵彻模拟中，ABAQUS和LS-DYNA 模拟的弹道极限均高于实验值，而PAM-CRASH 模拟的弹道极限恰恰相反（由于平头形弹体在弹道极限附近，实验的初速度较接近，因此图中不能清楚展示）。具体平均相对误差见表1，当计算所有数据的平均相对误差时，3 种软件模拟结果的误差基本在15%～25%之间。较大的误差主要来源于弹道极限附近的模拟结果，因为弹道极限附近剩余速度的绝对值较小，相对误差很大。去除掉弹道极限附近速度后，可以观察到所有软件模拟结果的平均相对误差均低于10%，大部分在5%以下。

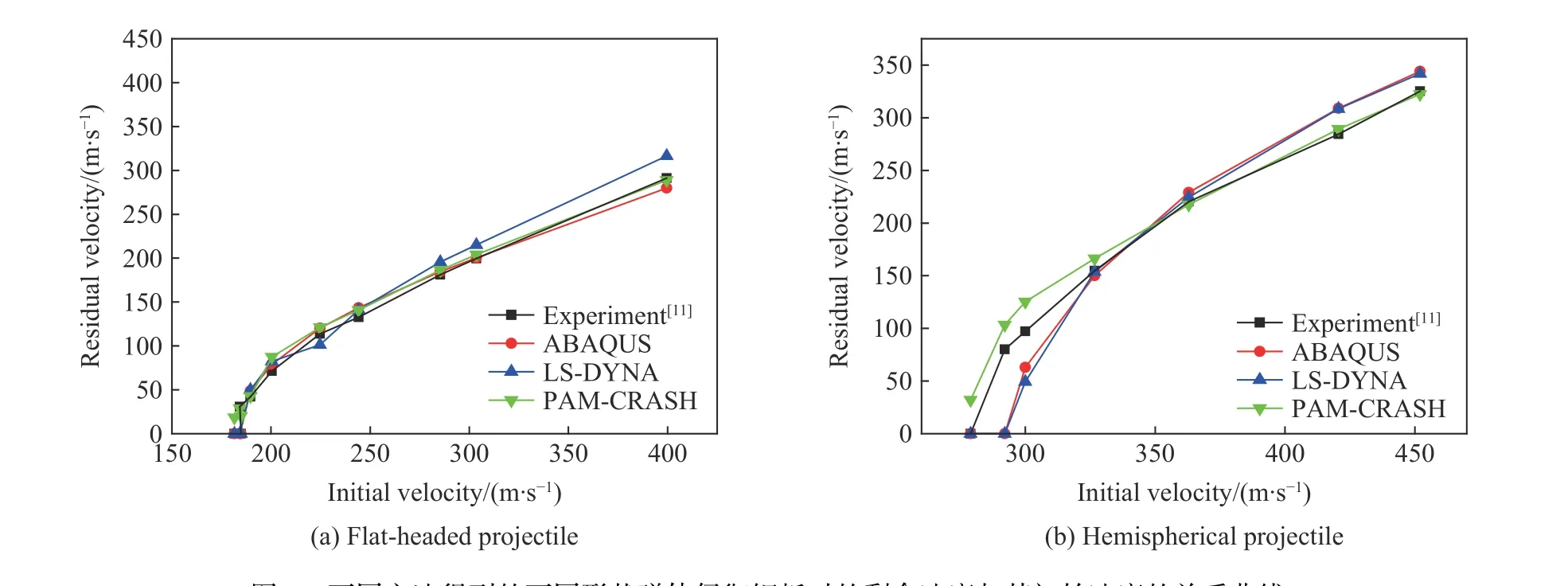
图6 不同方法得到的不同形状弹体侵彻钢板时的剩余速度与其初始速度的关系曲线Fig. 6 Changes of projectile residual velocities with their initial velocities obtained by different methods for penetration of the projectiles with different nose shapes into steel targets

表1 弹体剩余速度平均相对误差对比分析Table 1 Comparative analysis of the average relative error of the residual projectile velocity

图7～8 为3 种有限元软件对弹体直径和长度变形量的模拟结果与实验结果的对比。首先，从图7～8 可以很直观地看到，LS-DYNA 软件的模拟结果与实验结果偏离较大，在弹体变形量方面，LS-DYNA 的模拟结果不能很好地反映真实情况。其次，从表2 可以发现，对于2 种形状的弹体，ABAQUS 对弹体直径变化量的模拟结果与实验结果最接近，平均相对误差为分别为18.51%和22.32%，而PAM-CRASH 的则为48.00% 和87.91%；在弹体长度变形量方面，平头形弹体的PAM-CRASH 模拟效果更好，平均相对误差为22.35%，ABAQUS 的为30.19%。尽管ABAQUS 和PAMCRASH 的模拟结果优于LS-DYNA 的模拟结果，但误差仍旧偏大。经过查文献和分析认为，产生此类误差的主要原因可能有3 个：(1)本文中由于弹体屈服强度较高（1.9 GPa），因此计算中设置为弹性，而真实侵彻实验中则有可能发生局部塑性变形；(2)在实验和模拟结果的测量过程中测量误差难以避免，考虑到弹体的变形量是毫米量级，所以0.1 mm 的测量误差就会引起极大的差别；(3)实验中弹体测量是在弹性回复之后，而在模拟中则没有考虑弹性回复的问题。最后需要指出的是，本次模拟主要研究内容为靶板的破坏，对弹体的本构模型以及网格等未进行深入的对比研究。

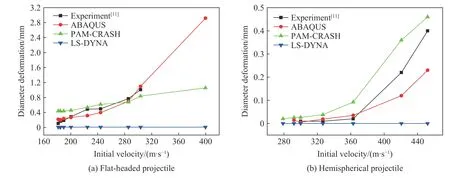
图7 不同方法得到的不同形状弹体侵彻钢板时的弹体直径变形量与其初始速度的关系曲线Fig. 7 Changes of projectile diameter deformations with their initial velocities obtained by different methods for penetration of the projectiles with different nose shapes into steel targets

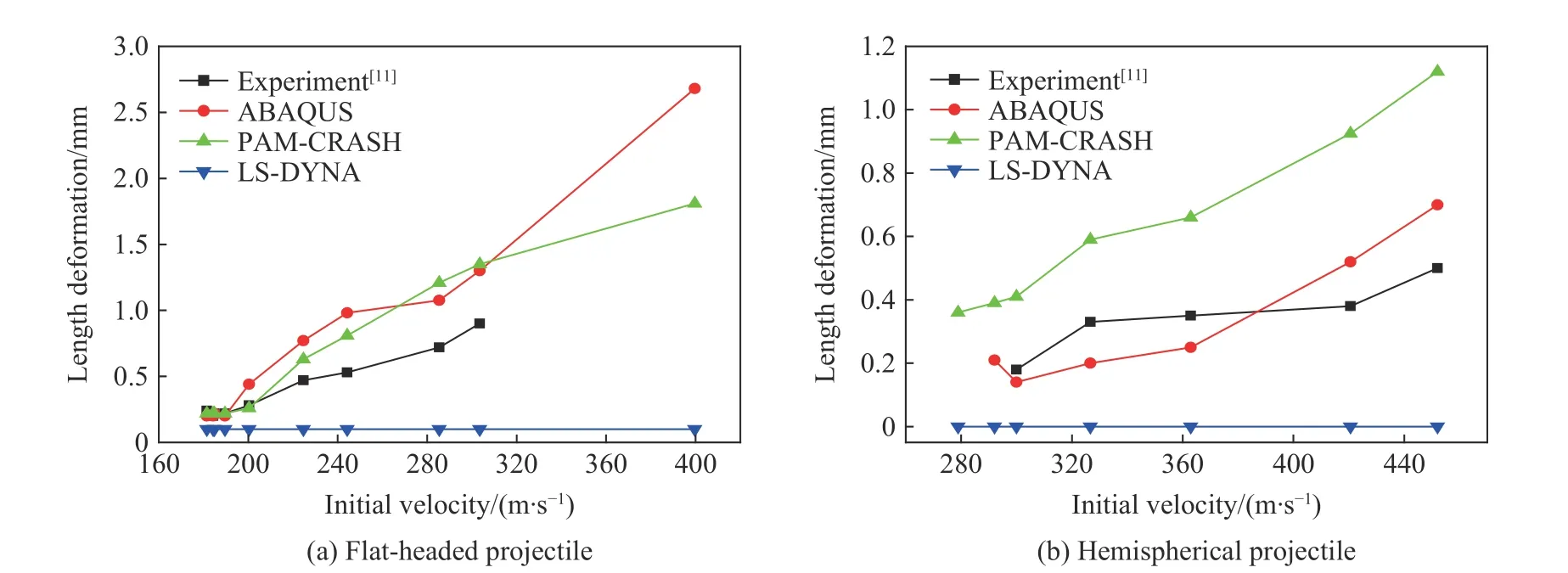
图8 不同方法得到的不同形状弹体侵彻钢板时的弹体长度变形量与其初始速度的关系曲线Fig. 8 Changes of projectile length deformations with their initial velocities obtained by different methods for penetration of the projectiles with different nose shapes into steel targets

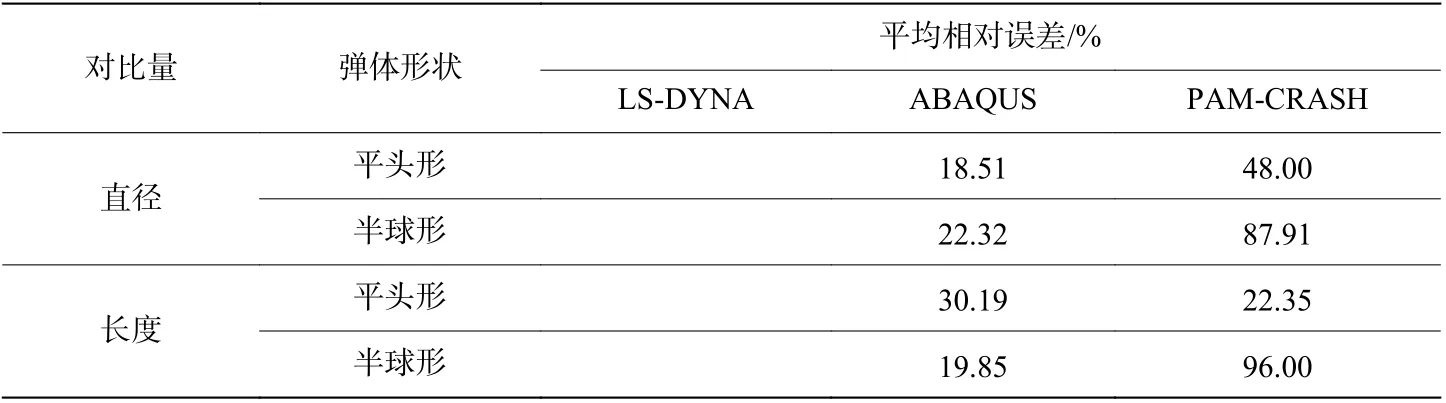
表2 弹体变形量平均相对误差对比分析Table 2 Comparison of the average relative error of the projectile deformation

2.4 靶板参数模拟结果对比分析

冲塞块飞出是靶板最主要的失效模式。图9 为平头形和半球形弹体冲塞块速度的模拟结果与实验结果的对比。从图9 可以看出，3 种有限元软件模拟的冲塞块速度与实验结果大致吻合。在不含临近弹道极限的模拟误差时，3 种软件模拟得到的结果偏差均低于15%，多数低于10%。其中PAM-CRASH 模拟结果误差最小，ABAQUS 次之。具体平均相对误差可见表3。

表3 冲塞块速度平均相对误差对比分析Table 3 Comparison of the average relative error of plug velocity

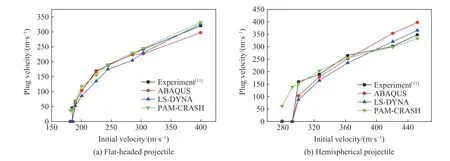
图9 不同方法得到的不同形状弹体侵彻钢板时冲塞块速度与弹体初始速度的关系曲线Fig. 9 Changes of plug velocity with initial projectile velocity obtained by different methods for penetration of the projectiles with different nose shapes into steel targets

图10 为不同有限元软件中靶板最大变形量的模拟结果与实验结果的对比。从图10 中可观察到，模拟结果与实验结果的变化趋势保持一致，随着弹体初速度的提高，最大变形量逐渐递减，这也符合Calder 等的理论。在ABAQUS 软件中，当弹体初速度较低时，弹体速度接近弹道极限速度，此时靶板最大变形量模拟结果出现较大误差，因此在起始点存在跳跃。此外，所有软件的模拟结果均略高于实验结果，具体平均相对误差如表4 所示；并且可以发现，2 种弹体形状下，PAM-CRASH 的模拟结果与实验结果最接近，平均相对误差分别为19.58%和11.99%，而LS-DYNA 的平头形弹体模拟结果和ABAQUS的半球形模拟结果误差较大，分别为41.26%和28.45%。经过分析认为，如此大的误差可能是由2 个因素导致的：第1 个因素是测量方法，本文中的测量是在靶板冲塞孔上表面处均匀选取10 个节点，测量出10 个节点在侵彻速度方向的位移，然后取平均值，而关于实验中靶板最大变形量的测量方法，相关论文中并未提及；第2 个因素是因为数值模拟的结果是在断裂后获得的，而相应的实验结果是在靶板的弹性回弹之后测量的，可能会引起一定误差。

表4 靶板最大变形量平均相对误差对比分析Table 4 Comparison of the average relative error of maximum deformation of the target

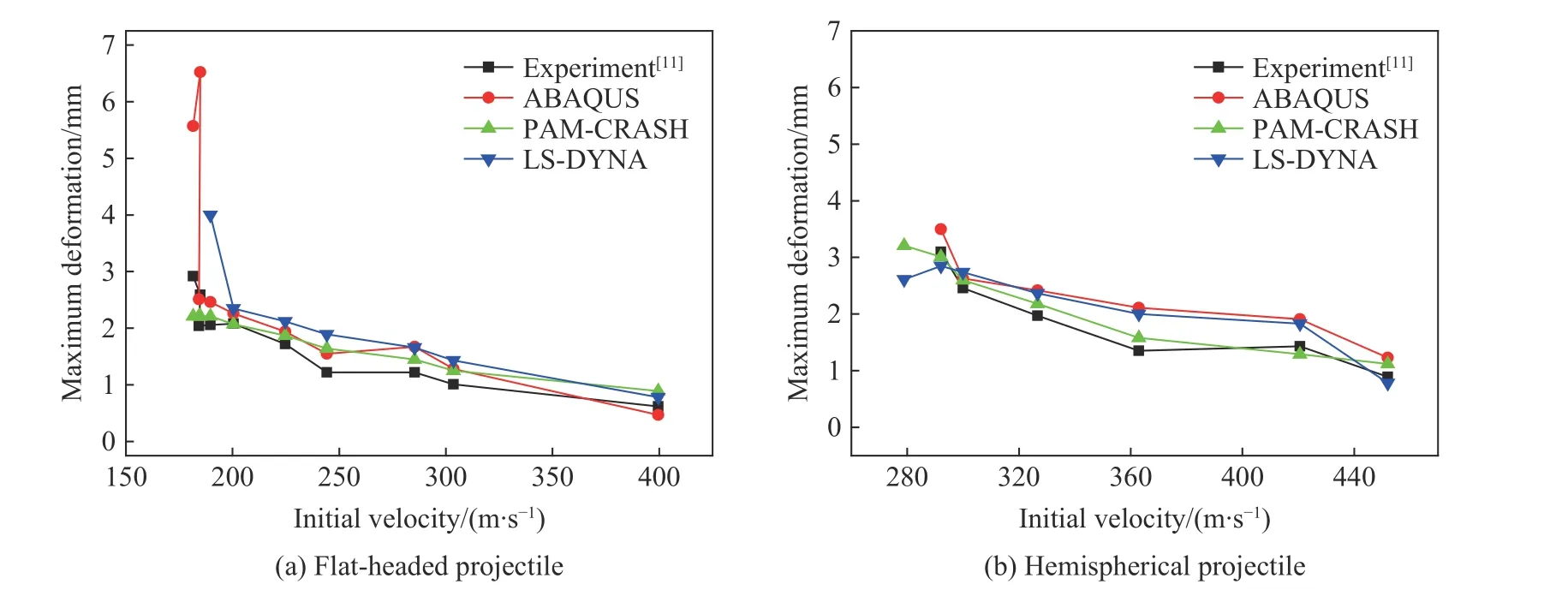
图10 不同方法得到的不同形状弹体侵彻钢板时靶板最大变形量与弹体初始速度的关系曲线Fig. 10 Changes of the maximum deformations of the targets with initial projectile velocity obtained by different methods for penetration of the projectiles with different nose shapes into steel targets

2.5 各软件计算结果的鲁棒性分析

数值模拟中，有部分参数无法通过实验获得，只能使用默认值或者凭借计算人员的经验进行设置，给模拟结果带来了很大的不确定性。如果软件模拟结果对这些参数的依赖性很强，那么无疑会增大软件的使用难度，同时也对使用者提出了更高的要求。本节中，对网格密度、摩擦因数、惩罚刚度缩放因数、接触刚度、黏性阻尼因数等不易通过实验获得的参数进行了对比分析，获得了利用3 种软件模拟侵彻问题时模拟结果的鲁棒性。

在模拟过程中，设置一组基准有限元参数（即2.2～2.4 节中的计算参数）。当研究某一参数的变化对模拟结果的影响时，其他参数均被设置成基准参数，并保持恒定。

结合Børvik 等所做的实验，利用LS-DYNA 进行平头形和半球形弹体侵彻12 mm 厚靶板的模拟，靶板材料为钢板，型号为Weldox 460E。对平头形弹体和半球形弹体各建立3 种计算模型，接触区域靶板网格单元尺寸分别为0.30、0.20、0.15 mm，弹体采用基准网格密度1 mm。

图11～13 为不同靶板网格密度对平头形弹体剩余速度及冲塞块速度模拟结果的影响。图14～15 为不同靶板网格密度对半球形弹体剩余速度及冲塞块速度模拟结果的影响。弹体节点选取自平头形弹体和半球形弹体底面中心点，冲塞块节点选自冲塞块底面中心点。在远离弹道极限（平头形弹体弹道极限为189 m/s，半球形弹体为292 m/s）的399.6 和452.0 m/s 时，靶板网格单元尺寸的逐渐增大对于弹体剩余速度及冲塞块速度模拟结果影响不大。而临近弹道极限时，不同形状弹体对于网格依赖性则表现不同，半球形弹体几乎依旧保持网格无关性，当靶板网格单元尺寸依次为0.15、0.20、0.30 mm 时，剩余速度及冲塞块速度变化趋势很小，基本可以忽略。而当平头形弹体初始速度为200.4 m/s，靶板网格单元尺寸为0.20、0.30 mm 时，剩余速度及冲塞块速度最后均趋近于零，即在模拟结果中表现为靶板未被打穿，弹体速度降为零，这显然与实验结果不符，为此又选取了平头形弹体初速度为224.7 m/s 进行模拟，模拟结果与之前类似。因此，在不同的网格密度下，平头形弹体剩余速度和冲塞块速度不同，随着靶板网格单元尺寸的增大，弹体剩余速度及冲塞块速度均逐渐降低，且靶板网格单元尺寸为0.15 mm 时，模拟结果最接近实验值。

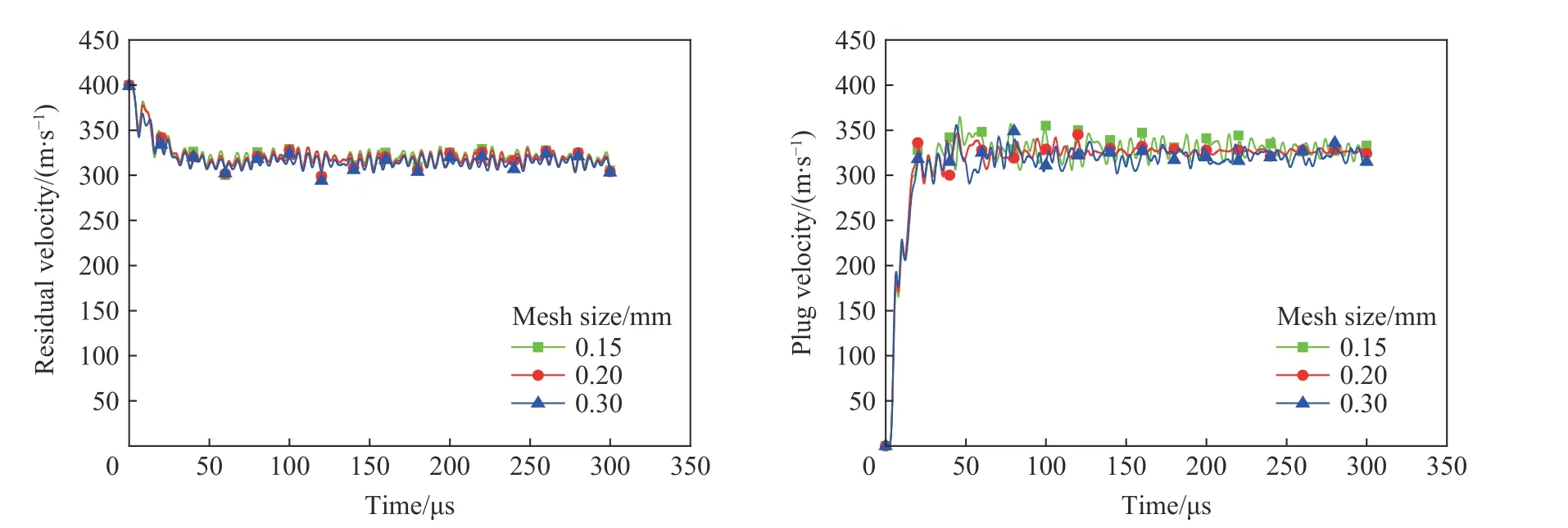
图11 采用LS-DYNA 模拟初始速度为399.6 m/s 的平头形弹体侵彻钢靶时，靶板网格单元尺寸对平头形弹体剩余速度和靶板冲塞块速度的影响Fig. 11 Influences of target mesh size on the projectile residual velocity and target plug velocity simulated by LS-DYNA for penetration of the flat-headed projectile with the initial velocity of 399.6 m/s into the steel target

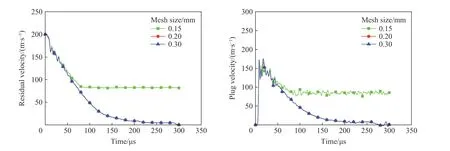
图12 采用LS-DYNA 模拟初始速度为200.4 m/s 的平头形弹体侵彻钢靶时，靶板网格单元尺寸对平头形弹体剩余速度和靶板冲塞块速度的影响Fig. 12 Influences of target mesh size on the projectile residual velocity and target plug velocity simulated by LS-DYNA for penetration of the flat-headed projectile with the initial velocity of 200.4 m/s into the steel target

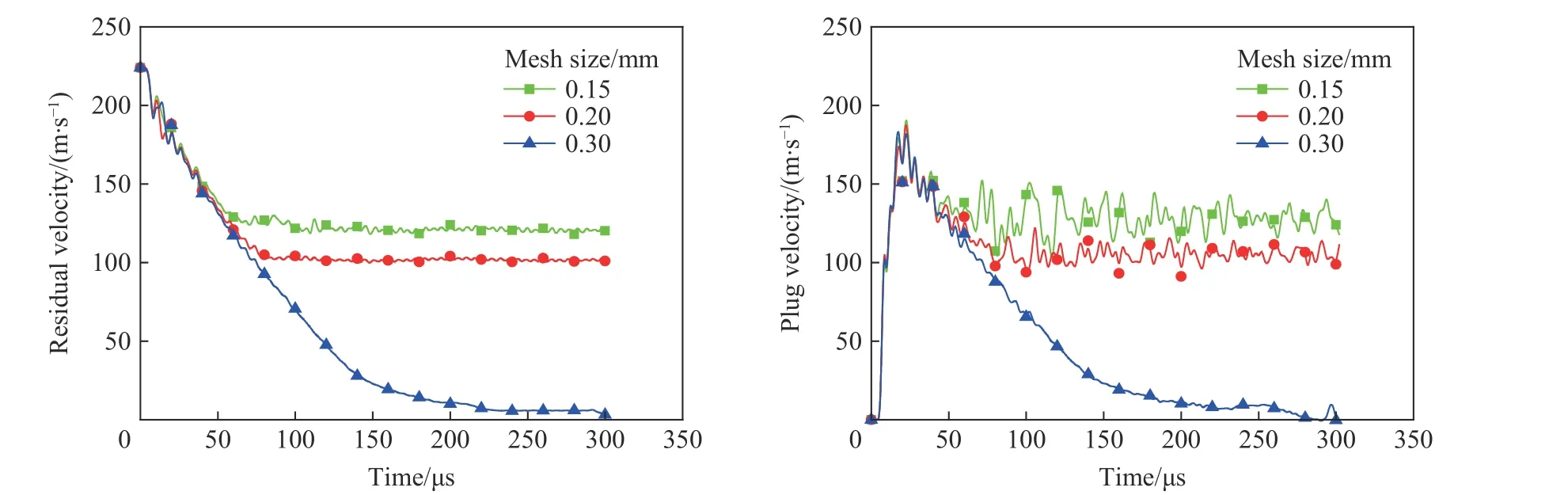
图13 采用LS-DYNA 模拟初始速度为224.7 m/s 的平头形弹体侵彻钢靶时，靶板网格单元尺寸对平头形弹体剩余速度和靶板冲塞块速度的影响Fig. 13 Influences of target mesh size on the projectile residual velocity and target plug velocity simulated by LS-DYNA for penetration of the flat-headed projectile with the initial velocity of 224.7 m/s into the steel target

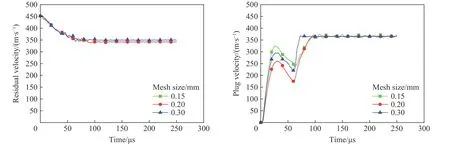
图14 采用LS-DYNA 模拟初始速度为452.0 m/s 的平头形弹体侵彻钢靶时，靶板网格单元尺寸对半球形弹体弹体剩余速度和靶板冲塞块速度的影响Fig. 14 Influences of target mesh size on the projectile residual velocity and target plug velocity simulated by LS-DYNA for penetration of the hemispherical projectile with the initial velocity of 452.0 m/s into the steel target

可以看出，靶板网格密度对于平头形侵彻模拟结果有一定影响，弹体着靶速度越临近弹道极限，模拟结果对网格的依赖性越强，其中网格单元尺寸为0.15 mm 时，模拟结果与实验结果最接近。对于半球形弹体的侵彻模拟，靶板网格单元尺寸的变化对模拟结果基本没有影响。因此，在用LS-DYNA 进行侵彻实验的相关模拟时，对平头形弹体的侵彻，接触区域的靶板网格选取0.15 mm 更合适，而对半球形弹体的侵彻要选取0.20 mm 更高效。

随后，探究摩擦因数对模拟结果的影响。给出5 组动摩擦因数值：0，0.1，0.3，0.5，1.0。使用LSDYNA 进行平头形和半球形弹体侵彻12 mm 厚靶板的模拟，靶板材料为钢板，型号为Weldox 460E。

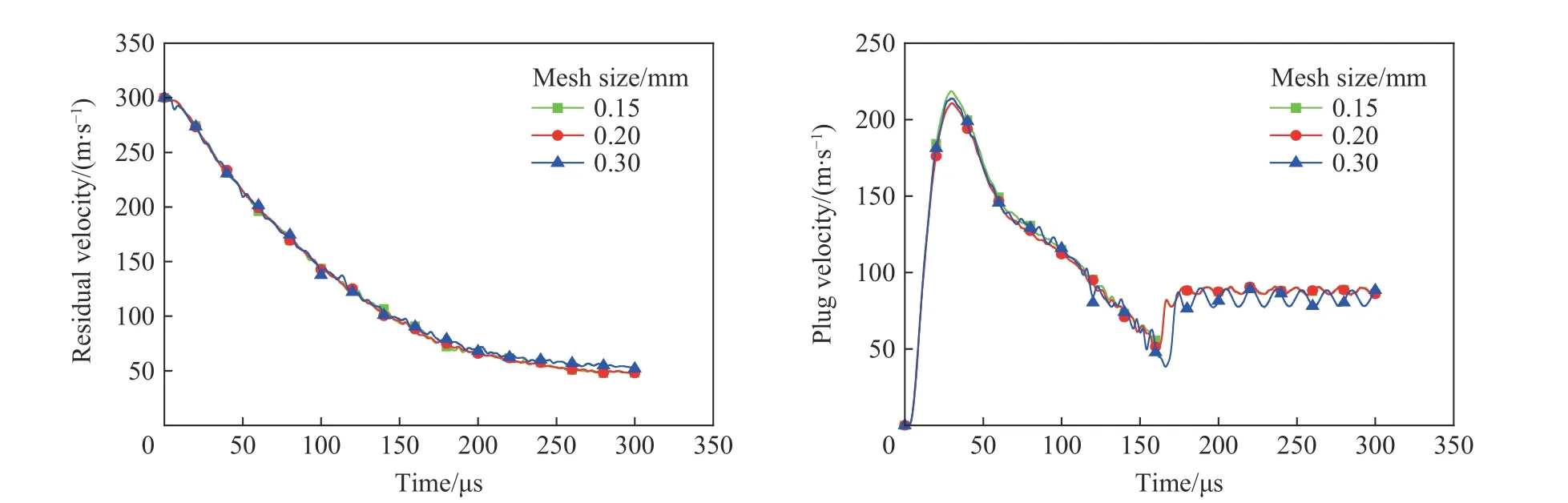
图15 采用LS-DYNA 模拟初始速度为300.0 m/s 的平头形弹体侵彻钢靶时，靶板网格单元尺寸对半球形弹体弹体剩余速度和靶板冲塞块速度的影响Fig. 15 Influences of target mesh size on the projectile residual velocity and target plug velocity simulated by LS-DYNA for penetration of the hemispherical projectile with the initial velocity of 300.0 m/s into the steel target

图16～17 为摩擦因数对弹体剩余速度及冲塞块速度的影响，节点位置与研究网格密度的节点保持一致。从图中可以看出，随着动摩擦因数的增大，无论是平头形弹体还是半球形弹体，其速度变化很小，几乎所有的数据线重合在一起，可知摩擦因数对LS-DYNA 模拟获得的剩余速度无影响。因此，在LSDYNA 的模拟中，弹体与靶板之间摩擦因数的变化对弹体剩余速度、冲塞块速度无影响。

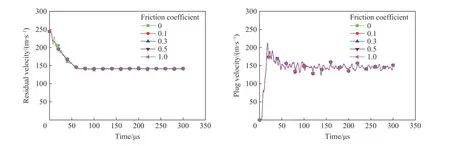
图16 采用LS-DYNA 模拟初始速度为244.2 m/s 的平头形弹体侵彻钢靶时，摩擦因数对平头形弹体剩余速度和靶板冲塞块速度的影响Fig. 16 Influences of friction coefficient on the projectile residual velocity and target plug velocity simulated by LS-DYNA for penetration of the flat-headed projectile with the initial velocity of 244.2 m/s into the steel target

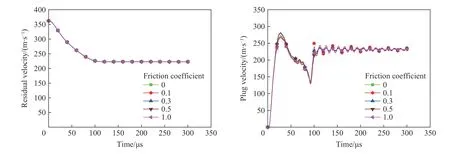
图17 采用LS-DYNA 模拟初始速度为362.9 m/s 的半球形弹体侵彻钢靶时，摩擦因数对弹体剩余速度和靶板冲塞块速度的影响Fig. 17 Influences of friction coefficient on the projectile residual velocity and target plug velocity simulated by LS-DYNA for penetration of the hemispherical projectile with the initial velocity of 362.9 m/s into the steel target

为研究接触刚度对模拟结果的影响，使用LS-DYNA 进行模拟，选取6 组不同的惩罚刚度缩放因数（SLSFAC）：0.05、0.10、0.20、0.30、0.40、0.50，在模拟过程中分别设置不同的惩罚刚度缩放因数进行计算分析。图18～19 为惩罚刚度缩放因数对弹体剩余速度及冲塞块速度的影响。节点位置与研究网格密度的节点保持一致，速度变化与惩罚刚度缩放因数无影响，可随机选取。从图18～19 可以看出，随着惩罚刚度缩放因数的增大，平头形弹体的剩余速度和冲塞块速度几乎不变，半球形弹体的冲塞块速度略有增长，但变化也很小，设置相邻惩罚刚度缩放因数的速度差在5 m/s 左右。

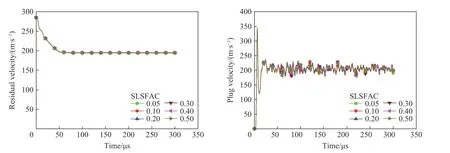
图18 采用LS-DYNA 模拟初始速度为285.4 m/s 的平头形弹体侵彻钢靶时，惩罚刚度缩放因数（SLSFAC）对弹体剩余速度和靶板冲塞块速度的影响Fig. 18 Influences of penalty stiffness scaling factors (SLSFACs) on the projectile residual velocity and target plug velocity simulated by LS-DYNA for penetration of the flat-headed projectile with the initial velocity of 285.4 m/s into the steel target

为研究黏性阻尼因数（viscous damping coefficient, VDC）对模拟结果的影响，使用LS-DYNA 进行模拟，选取7 组VDC 值，分别为0、10、20、30、40、50、60。将这7 组参数分别应用到数值模拟中，对比分析模拟结果。

图20～21 为黏性阻尼因数对弹体剩余速度及冲塞块速度的影响。节点位置与研究网格密度的节点保持一致，速度变化与黏性阻尼因数无影响，可随机选取。与惩罚刚度系数类似，从图20～21 中可以看出，随着黏性阻尼因数的增大，平头形弹体的剩余速度和冲塞块速度值保持恒定，而半球形弹体冲塞块速度有所降低，但变化也很小，最大差值为10 m/s 左右。

图19 采用LS-DYNA 模拟初始速度为326.7 m/s 的半球形弹体侵彻钢靶时，惩罚刚度缩放因数对弹体剩余速度和靶板冲塞块速度的影响Fig. 19 Influences of penalty stiffness scaling factor on the projectile residual velocity and target plug velocity simulated by LS-DYNA for penetration of the hemispherical projectile with the initial velocity of 326.7 m/s into the steel target

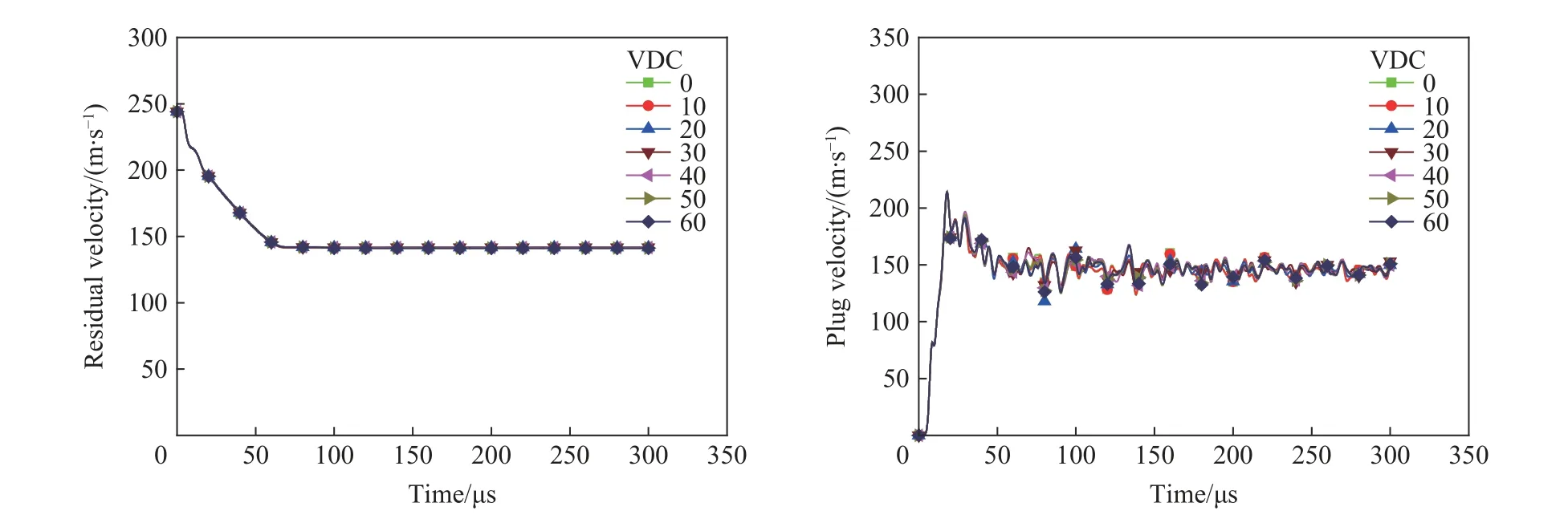
图20 采用LS-DYNA 模拟初始速度为244.2 m/s 的平头形弹体侵彻钢靶时，黏性阻尼因数（VDC）对弹体剩余速度和靶板冲塞块速度的影响Fig. 20 Influences of viscous damping coefficient (VDC) on the projectile residual velocity and target plug velocity simulated by LS-DYNA for penetration of the flat-headed projectile with the initial velocity of 244.2 m/s into the steel target

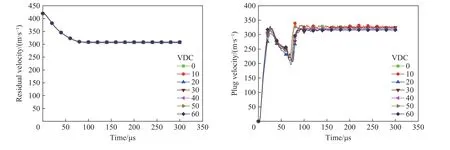
图21 采用LS-DYNA 模拟初始速度为420.6 m/s 的半球形弹体侵彻钢靶时，黏性阻尼因数对弹体剩余速度和靶板冲塞块速度的影响Fig. 21 Influences of viscous damping coefficient on the projectile residual velocity and target plug velocity simulated by LS-DYNA for penetration of the hemispherical projectile with the initial velocity of 420.6 m/s into the steel target

采用相同方法研究了ABAQUS 和PAM-CRASH 的模拟结果对于模型参数的依赖性，将主要有限元模型参数对3 种软件数值模拟结果的影响总结如表5～7 所示，表中：无影响指影响幅度小于1%；有一定影响指影响幅度为1%～10%，影响较大指影响幅度大于10%。需要指出的是，上文关于3 种软件模拟结果的误差分析中，均采用了最佳网格尺寸的模拟结果。

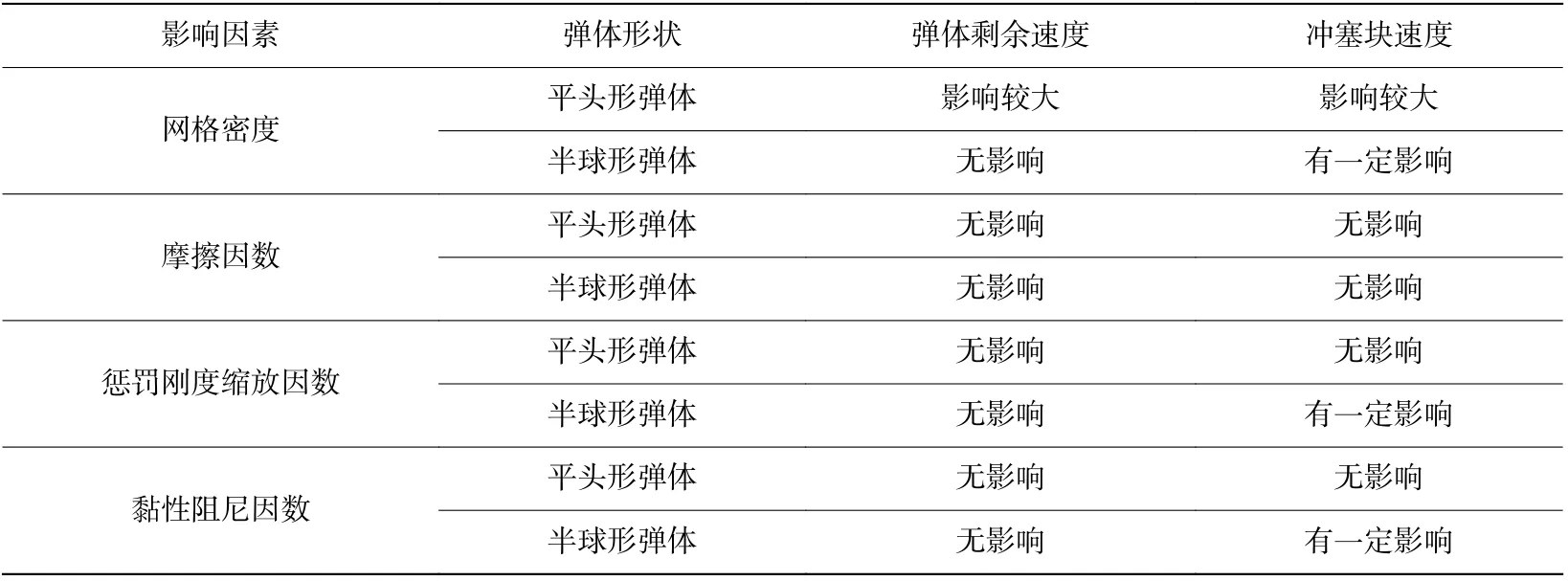
表5 主要有限元模型参数对LS-DYNA 数值模拟结果的影响Table 5 Influences of main finite element parameters on the numerical simulation results of LS-DYNA

从表5 可以看出，各模型参数对LS-DYNA 模拟结果影响不大，仅平头形弹体的数值模拟结果受网格单元尺寸影响较大，LS-DYNA 鲁棒性较好。结合表6 发现，模型参数对ABAQUS 模拟结果均有所影响，其中网格尺寸对平头形弹体及摩擦因数对半球形弹体侵彻模拟效果影响较大。而表7 表明，PAMCRASH 对参数的设置最敏感，几乎所有模型参数均对于其模拟结果有较大影响。

表6 主要有限元模型参数对ABAQUS 数值模拟结果的影响Table 6 Influences of main finite element parameters on the numerical simulation results of ABAQUS

表7 主要有限元模型参数对PAM-CRASH 数值模拟结果的影响Table 7 Influence of main finite element parameters on the numerical simulation results of PAM-CRASH

2.6 其他因素及差异对比分析

本文的模拟是在相同状况下的Inter(R) Xeon(R) CPU E5-2650 v4@ 2.20GHz 处理器、96.0 GB 内存的计算机上进行。当网格单元尺寸较大时模拟得到的弹道极限远小于实验值，结果不符合要求，因而必须增大接触区域的网格密度。然而，随着网格密度的加大，计算时长也随之增长。为获得合适的模拟结果，ABAQUS 和LS-DYNA 软件中靶板网格单元尺寸为0.20 mm，PAM-CRASH 软件中靶板网格单元尺寸则为0.30 mm，导致计算所耗时间也有所差异，如表8 所示。

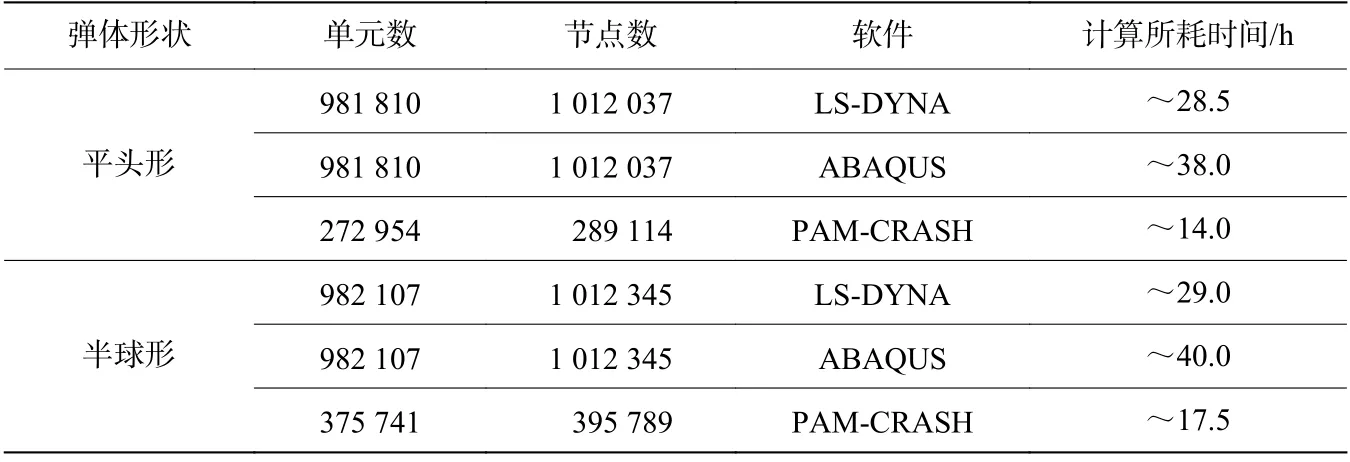
表8 不同软件计算时长比较Table 8 Comparison of the calculation time of different software

在计算过程中，发生错误导致计算不能进行是难以避免的。其中ABAQUS 报错率最高，包括网格扭曲过大、单元形变速度与膨胀波速之比大于1 等一系列问题，主要解决方式是提高网格质量，调整最小步长；使用PAM-CRASH 中最常见的错误是出现负体积问题，主要解决方式是提高网格质量和适当调整接触厚度，另外，PAM-CRASH 自带的网格划分质量偏低；而LS-DYNA 则报错率不高，可修改K 文件或者卡片输入，较方便。

由于应用广泛，ABAQUS 和LS-DYNA 的参考书籍丰富，并且手册详细，可以通过多途径解决问题。而PAM-CRASH 使用人员相对较少，学习类书籍偏少，并且手册中有些知识介绍比较简略。

3 种软件都是功能强大的有限元分析软件，每种软件都有自己的独特之处，在模拟时3 种软件也有所差异：在材料的模型材料输入中，ABAQUS 和LS-DYNA 均输入了Grüneisen 状态方程，而PAMCRASH 没有输入；PAM-CRASH 在输入J-C 本构和失效准则参数时，都忽略了温度项，且与温度相关的其他参数都未输入；考虑到软件中内嵌的J-C 断裂准则与常规的J-C 断裂准则表达式有差别，ABAQUS 和PAM-CRASH 在取值时，需要取其相反数；在接触设置上，LS-DYNA 和PAM-CRASH 均设置了接触刚度，而ABAQUS 则为“硬接触”；在固支方式上，ABAQUS 和PAM-CRASH 是全部约束四周边界，而LS-DYNA 则是参考时党勇等的方法，定义了非反射边界。以上是3 种有限元软件在此次模拟中的相关差异。但在材料的建模方式、网格划分、材料参数的确定和输入保持了统一，最大程度控制相对变量，因此模拟结果是具有可比性的。

3 总 结

本文中，基于金属靶板侵彻实验，全面对比分析了LS-DYNA、ABAQUS、PAM-CRASH 等3 种有限元软件模拟结果与实验结果的差异，包括失效模式、弹体剩余速度、弹体变形量、冲塞块速度、靶板变形量以及客观因素等。结果表明，3 种软件模拟结果与实验的破坏模式十分类似。平头形弹体是冲塞破坏，半球形弹体是拉伸破坏；在弹体剩余速度、冲塞块速度2 个方面，模拟结果与实验结果大体上吻合；平头形弹体侵彻模拟效果稍好于半球形弹体；模拟数据的平均相对误差普遍低于20%，其中PAMCRASH 误差最小，LS-DYNA 相对较大。但在弹体变形量和靶板变形量的对比上，由于子弹材料设置为弹性，3 种软件得到的结果偏差均较大。此外，3 种软件各有特点，如ABAQUS 和LS-DYNA 计算获得的弹道极限高于实验值，而PAM-CRASH 则低于实验值；ABAQUS 报错率最高，在计算时长和模拟效果上较平衡；LS-DYNA 报错率低，鲁棒性较好，模型参数的变化对其计算结果影响不大；PAM-CRASH 受模型输入参数影响较大。本文的结论是基于靶板材料为Weldox 460E 钢、弹体为ARNE 工具钢、冲击速度为180～450 m/s 的条件下获得的，但是对于其他材料在此速度范围内的侵彻问题计算也有指导意义。