基于响应面法的纤维金属层合板抗弹性能优化设计*

孔祥韶，杨 豹,2，周 沪,2，郑 成，刘 芳，吴卫国

（1. 武汉理工大学绿色智能江海直达船舶与邮轮游艇研究中心，湖北 武汉 430063；2. 武汉理工大学船海与能源动力工程学院，湖北 武汉 430063；3. 武汉理工大学交通与物流工程学院，湖北 武汉 430063）

纤维金属层合板是由纤维增强复合材料与金属或金属合金交替层铺而成的新型复合结构，由于其具有优异的强度、刚度、耐腐蚀、耐疲劳以及冲击吸能等性能，在航天航空、汽车以及船舶等行业都存在巨大的应用潜力。纤维增强复合材料本身具有各项异性、界面差异性较大、设计灵活多变等特点，且金属层和纤维层的厚度以及排列顺序也会对层合板的抗弹吸能特性产生一定影响。因此，开展纤维金属层合板优化设计研究对其力学性能增强和轻量化具有重要意义。

近年来，学者们对于复合材料结构的设计和优化开展了大量研究工作，通过对复合材料的铺层方案进行优化设计，显著减小了结构质量，且制造工艺和结构强度也可以满足要求；通过采用遗传算法对复合材料层间黏结参数进行优化设计，可显著提升其拉伸和剪切强度。复合材料结构动态响应和吸能等特性优化也受到了研究人员的关注，Mostofi 等采用响应面法对聚脲-铝层合板结构进行优化设计，得到了冲击载荷作用下层合板中心永久变形最小时的铝板厚度、聚脲层厚度和总预爆压力，并验证了优化方案的合理性；王振等基于响应面模型开展了复合材料锥形圆管结构的优化设计，优化后的单向碳纤维复合材料圆锥管的比吸能提高了15.6%，初始峰值载荷降低了51.8%，质量减小了22.4%；顾杰斐等基于变刚度层合板的抗屈曲机制建立了一种铺层优化设计方法，通过遗传算法得到了初步最优的铺层方案，通过与原方案对比，最优铺层方案的屈曲载荷提高了25.7%；冯振宇等确定了不同复合材料薄壁结构设计参数相关的响应面方程，采用序列二次规划算法对模型进行优化求解并验证了该方法的适用性。Cutolo 等结合理论分析和实验测试，以每层纤维方向为设计变量，以特定边界条件下的应变能为优化目标，得到了多层纤维的最佳排列，改善了结构的应力分布，提高了抗屈曲能力。Ghashochi-Bargh 等采用粒子群算法和有限条法对3 种不同边界条件的纤维金属层合板的固有频率响应进行了优化，以铺层角度、层数、面板长宽比、金属板厚为设计变量，得到了使纤维金属层合板固有频率最大的设计方案。Arhore 等利用多层损伤有限元模型，基于遗传算法优化的方法研究了多层结构对纤维金属层合板冲击性能的影响，以每一铺层的厚度和纤维方向为设计变量对结构的吸能效果进行优化，得到了吸能效果良好的设计方案。

从目前已开展的研究工作来看，纤维金属层合板的优化目标多以减小结构质量为主。层合板在受到弹体高速冲击时的抗弹吸能效果需给予考虑和关注。响应面分析法（response surface methodology，RSM）在对结构耐撞性、结构可靠性等方面的优化应用研究较多，而该方法在高速冲击下结构吸能优化方面开展的研究较少。本文中，以提升纤维金属层合板的抗弹吸能性能为目标，采用响应面分析法，分别以纤维铺层方向、金属层和复合材料层厚度为设计变量，对纤维金属层合板进行优化设计，以期为纤维金属层合板的抗弹设计提供一定参考。

1 弹体冲击纤维金属层合板过程的数值模拟

1.1 有限元模型参数

采用平面几何尺寸为1 00 mm×100 mm 的纤维金属层合板作为研究对象，纤维增强材料为玻璃纤维增强聚丙烯（glass fiber reinforced polypropylene, GFPP），如图1 所示。分别定义下层Al、中间层Al、上层Al（靠近弹体一侧）的厚度为、、以及纤维层厚度为。材料的各项性能参数见表1～2。表中：ρ 为密度，、、分别为纤维方向弹性模量、横向弹性模量和厚度方向弹性模量，、、分别为纤维面内泊松比、纤维和厚度方向面内泊松比、横向和厚度方向面内的泊松比，、、分别为纤维面内剪切模量、纤维和厚度方向面内剪切模量、横向和厚度方向面内的剪切模量，、分别为纤维方向的拉伸强度和压缩强度，、分别为横向拉伸强度和横向压缩强度，、、分别为纤维面内剪切强度、纤维和厚度方向面内剪切强度、横向和厚度方向面内的剪切强度。铺层形式为A3G23，即铝合金薄板的数量为3，每层厚为0.5 mm，纤维增强材料叠合块的数量为2，每块厚度为1 mm，每个纤维增强材料叠合块中的GFPP 层数为3。优化前的层合板总质量为78.70 g。弹头直径为10 mm，弹体长15 mm，初始速度为200 m/s。

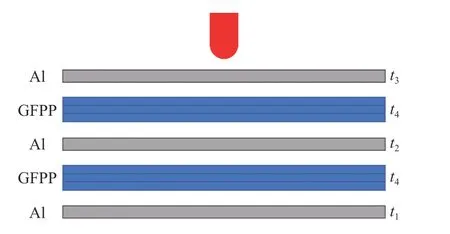
图1 A3G23 层合板铺层方案示意图Fig. 1 Schematic diagram of A3G23 laminate layup scheme

表1 热塑性纤维增强材料的弹性参数Table 1 Elastic parameters of thermoplastic fiber reinforced materials

表2 热塑性纤维增强材料的强度参数Table 2 Strength parameters of thermoplastic fiber reinforced materials

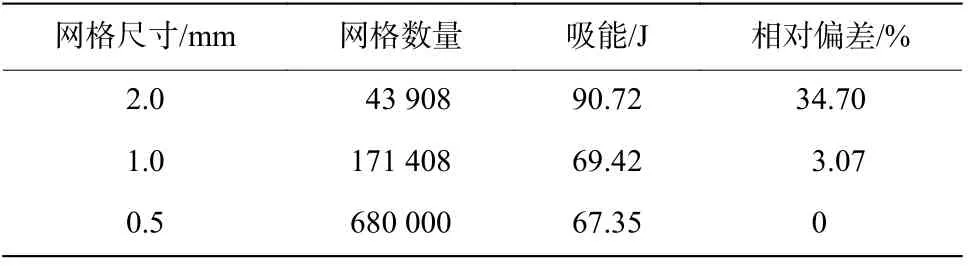
表3 网格收敛性分析Table 3 Analysis of grid convergence

表4 Cohesive 单元的材料参数[16]Table 4 Material parameters of the cohesive element[16]

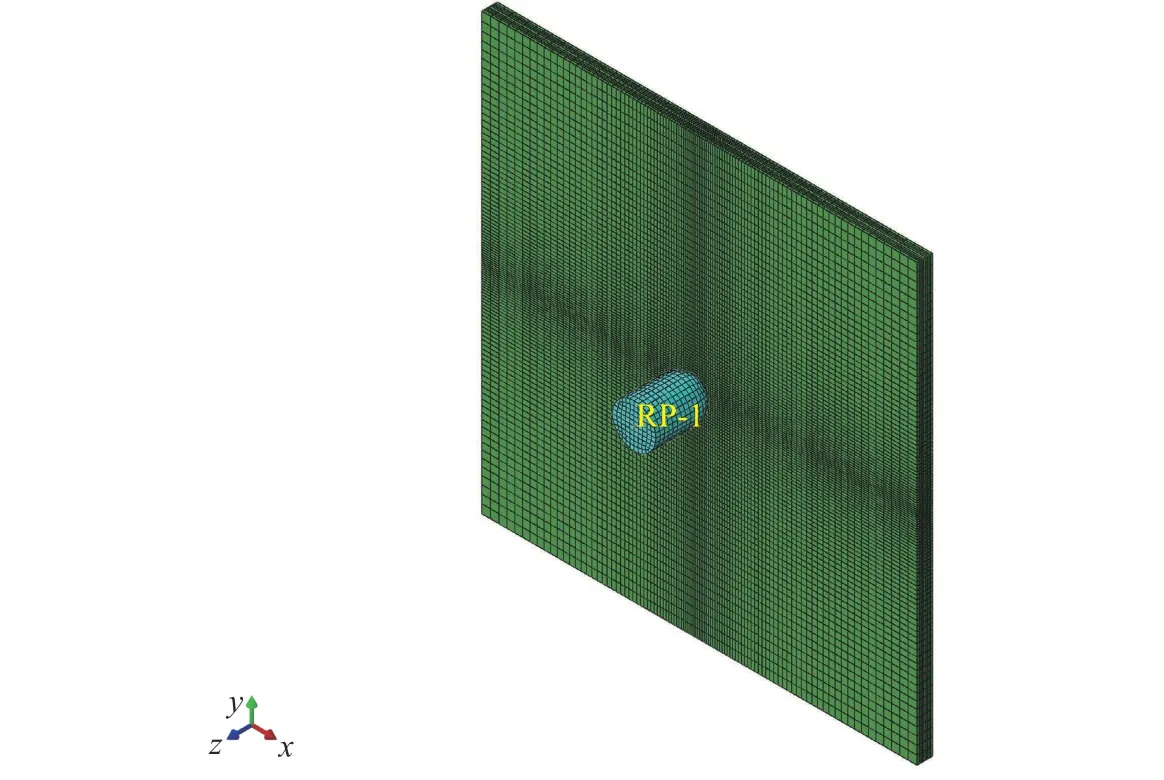
图2 优化前的层合板模型Fig. 2 The original laminate model

1.2 实验验证及结果分析

为验证所采用的数值模拟方法的准确性，以纤维金属层合板的高速冲击实验为研究对象，对3Al(6-O)/2G 型纤维金属层合板的穿甲实验进行模拟分析，实验中采用高压气枪对弹体加速，层合板前设置测速示波器，层合板后设置2 台高速摄影仪，分别用于测量弹体的初速度和剩余速度，进而得到层合板的吸能情况，实验布置如图3 所示。将实验与数值模拟结果进行对比分析，如表5 所示。可以看到，数值模拟所得弹体剩余速度与实验结果吻合较好，各工况模拟结果与实验结果的相对误差均在5%以内。对于3Al(6-O)/2G 型纤维金属层合板，实验及数值模拟中弹体侵彻后的剩余速度与初速度的拟合公式为：

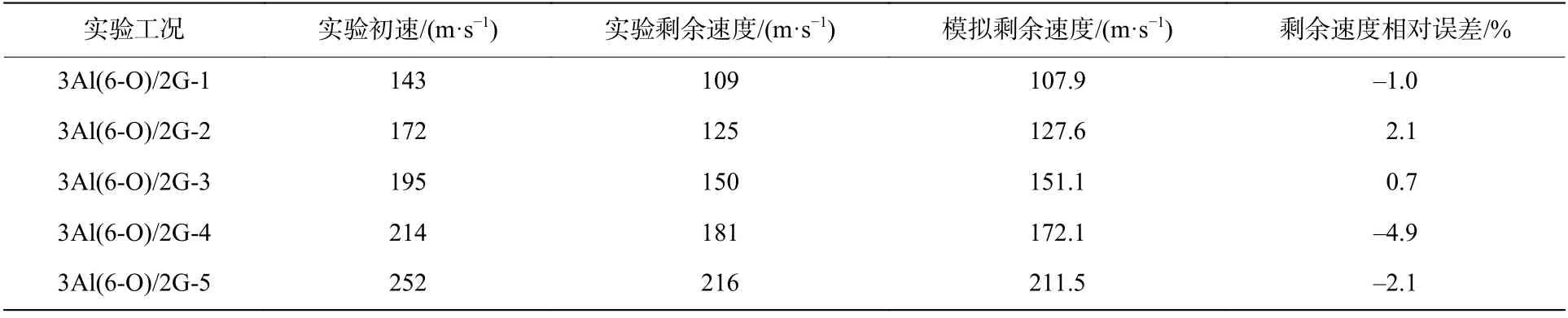
表5 弹体剩余速度实验结果与数值模拟结果对比Table 5 Comparison of projectile residual velocities between experimental and numerical results

图3 纤维金属层合板高速冲击实验布置Fig. 3 Layout diagram of high-speed impact experiment for fiber metal laminates

式中：为弹体剩余速度，为弹体初始入射速度，为层合板弹道极限速度，和为拟合参数。

所得弹道极限速度为118 m/s，如图4 所示。以弹体入射速度为172 m/s 的工况为例，实验与数值模拟所得纤维金属层合板破坏形貌如图5～6 所示，纤维金属层合板中部分纤维发生拉伸断裂，铝合金背板产生大范围的塑性变形，进一步撕裂形成花瓣状并造成穿孔，铝合金与纤维之间的分层主要分布在冲击附近区域。实验以及数值模拟中层合板的变形模式和穿孔形貌均吻合较好。通过以上对比验证，说明本文中的数值模拟方法具有较高的准确性，可进一步用于层合板优化方案的计算分析。

图4 弹体剩余速度与入射速度的关系曲线Fig. 4 Change of projectile residual velocity with its incident velocity

图5 实验与数值模拟的纤维金属层合板横截面破坏形貌Fig. 5 Experimental and numerical failure morphologies of fiber-metal laminates (a cross-sectioned view)

图6 实验与数值模拟的纤维金属层合板背面破坏形貌Fig. 6 Experimental and numerical failure morphologies of fiber-metal laminates (a top view)

2 纤维金属层合板吸能优化分析

纤维金属层合板的纤维层具有设计灵活多变、材料各向异性等特点，因而可以通过改变材料相应的结构参数来调整其性能。层合板结构的性能设计可通过选择合适的铺设角度、各铺层的叠放顺序、各铺层厚度等方面展开。在铺层设计时，通常还需要综合考虑强度、刚度以及工艺制备等方面的要求。

2.1 纤维铺层方向优化分析

根据复合材料铺层优化设计方案的计算要求，优化后的铺层应当满足以下基本原则。

（1）考虑设计和生产制造的工作量，在满足受力的前提下，铺层方向数应该尽量少。工程上常采用0°、±45°、90°的标准铺层，以降低制造加工的复杂性。

（2）取向相同的铺层叠放不能超过2 层。

（3）上下两部分复合层铺设方向关于中间金属层均衡对称，防止拉-剪、拉-弯耦合引起固化后的翘曲变形。

（4）铺层取向按承载选取原则，铺层轴线应与内力拉压方向一致，最大限度地利用纤维轴向具有高强度和高刚度的特性。其中，0°为主方向，主要承受纵向载荷；90°有利于调节泊松比和改善横向强度；±45用来承受剪切载荷。

（5）对于冲击载荷区的设计原则，需配置一定数量的与载荷方向成 ± 45的单层，以便将集中载荷扩散。表面纤维应均布于各个方向，使相邻层夹角尽可能小，目的是防止基体受载和减少分层。

基于上述原则，对纤维铺层方向进行方案设计，如表6 所示。分别对12 组铺层方案进行参数化建模计算。后续处理中分别提取各铺层方案中弹体的动能时程曲线，如图7 所示。

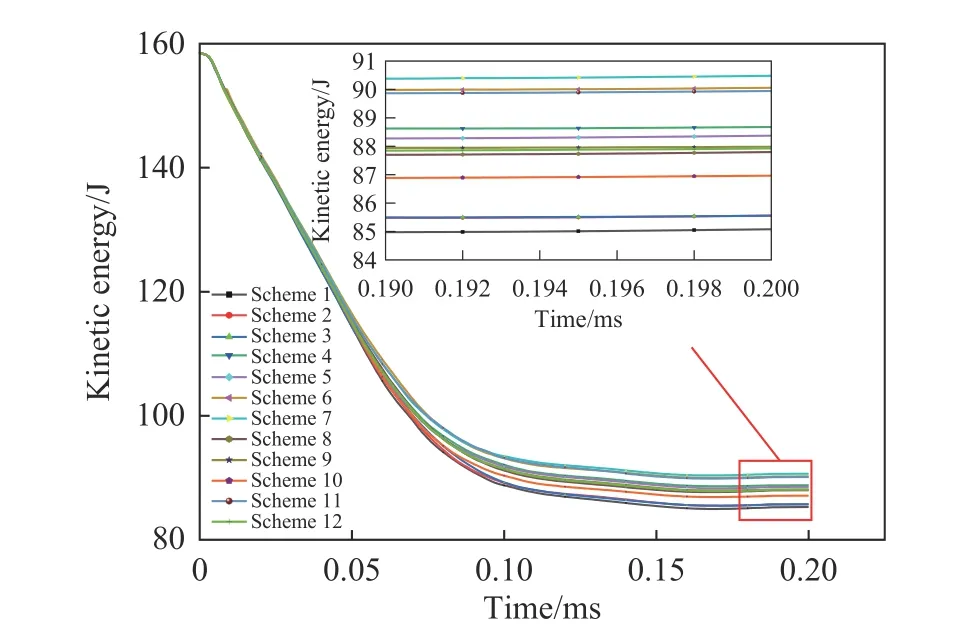
图7 不同铺层方向下弹体动能-时间变化曲线Fig. 7 Kinetic energy-time curves of projectile under different layup directions

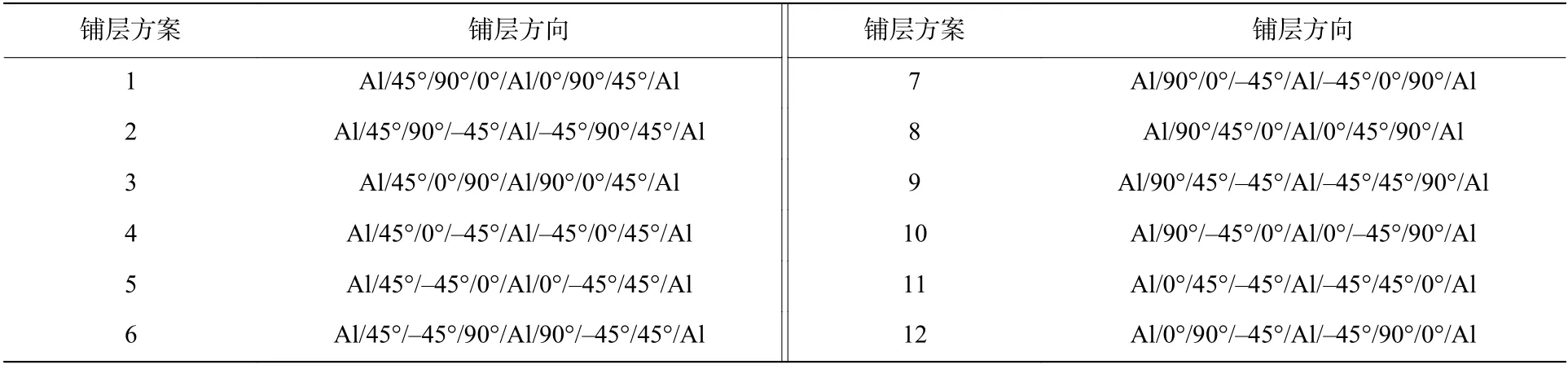
表6 纤维金属层合板铺层方案Table 6 Layer schemes of fiber metal laminates

图8 中直观展示了不同铺层方案的层合板吸能效果。其中铺层方案0 为优化前的层合板铺层方案。在上述12 种铺层方案下，铺层方案1 的抗弹吸能效果最好，因此在该铺层方案的基础上继续优化。

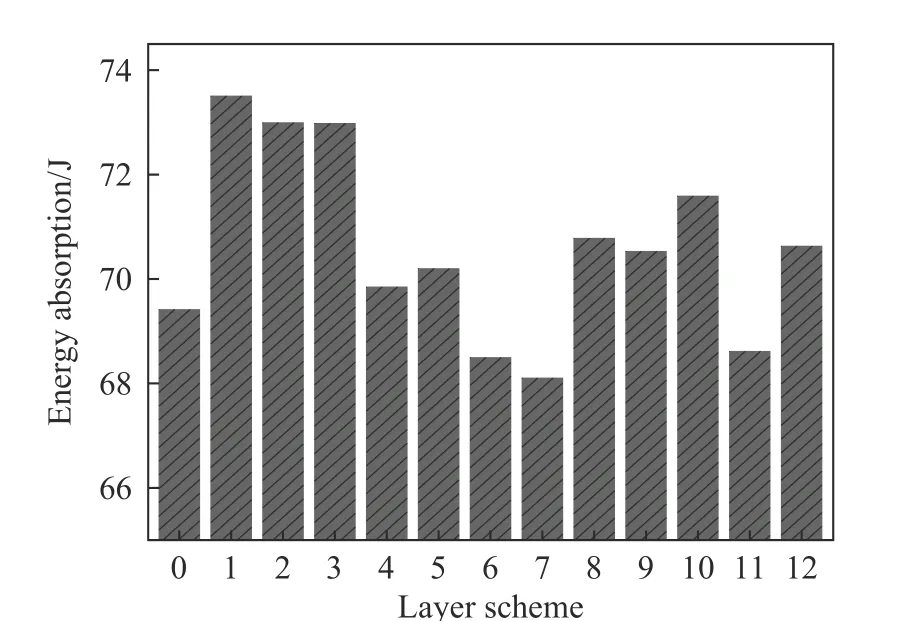
图8 不同铺层方案下层合板的吸能效果Fig. 8 Energy absorption effects of the lower laminates under different layer schemes

2.2 层合板铺层厚度优化分析

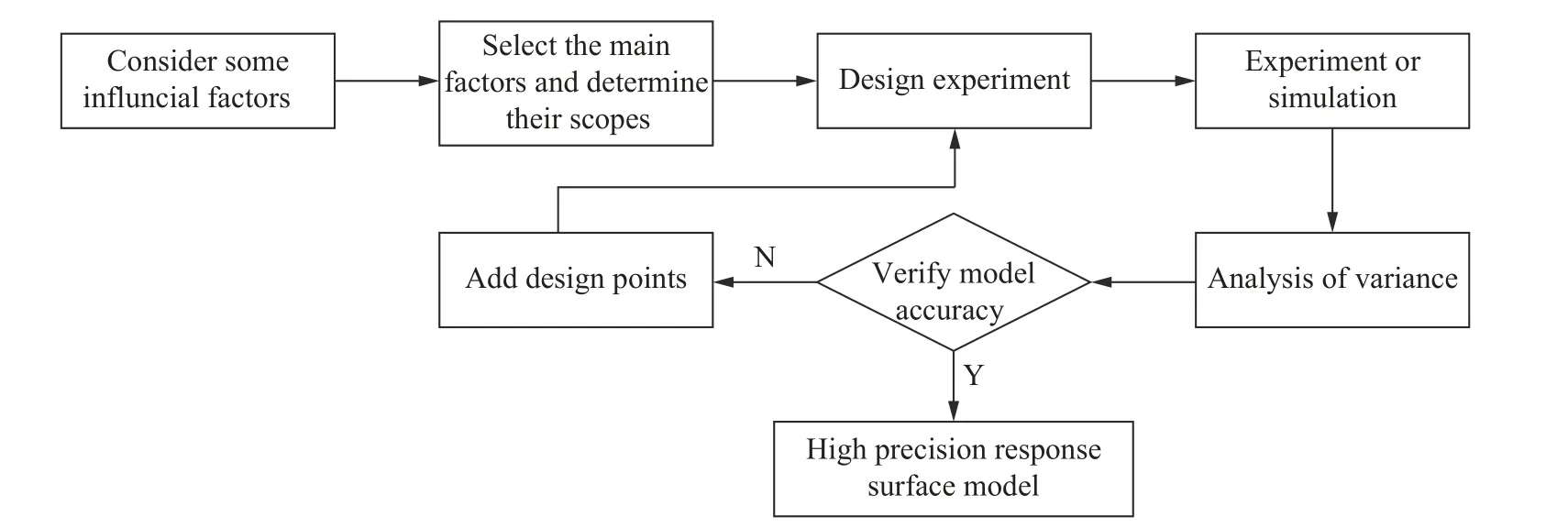
图9 响应面优化设计流程Fig. 9 Response surface optimization design process

各因子设计水平如表7 所示，对目标层合板进行BBD 实验设计，编码后实验设计方案，因子数为4，实验样本数为27。使用ABAQUS 分别对27 个样本进行参数化建模并计算，后处理中采集各样本的吸能和质量计算比吸能。实验设计方案和比吸能数据如表8 所示。使用MATLAB 对实验样本进行响应面设计，根据方差分析对模型进行优化，方差分析结果如表9 所示。其中，模型＜0.000 1，模型极显著，决定系数接近1，与调整决定系数相差不大，模型精度较高，可用于预测。4 个因子的均小于0.05，说明4 个因子对模型影响显著，即对比吸能的影响明显。在各因子交互项中，α×α、α×α之间影响显著，相互作用明显，响应面曲线和等高线分别如图10～11 所示。α×α、α×α、α×α之间相互作用不显著。因此，得到的二阶响应面模型为：

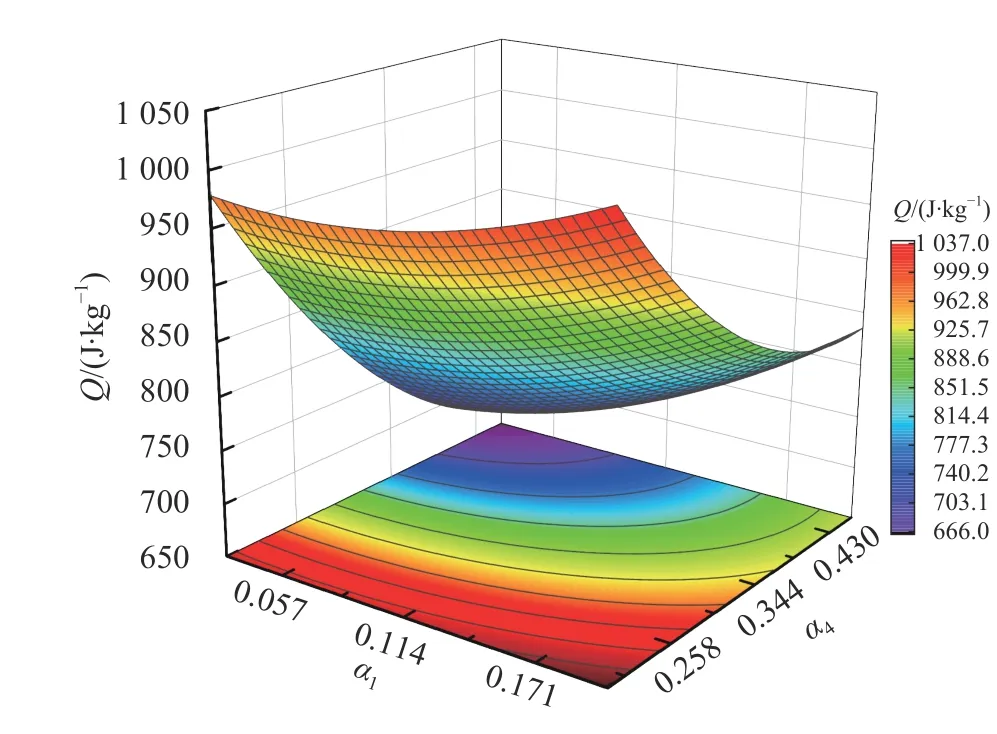
图10 α 1 和 α 4 交互作用对比吸能影响的响应面和等高线Fig. 10 Response surfaces and contour lines of interaction between α 1 and α 4 on specific energy absorption

表7 设计因子水平Table 7 Design factor levels

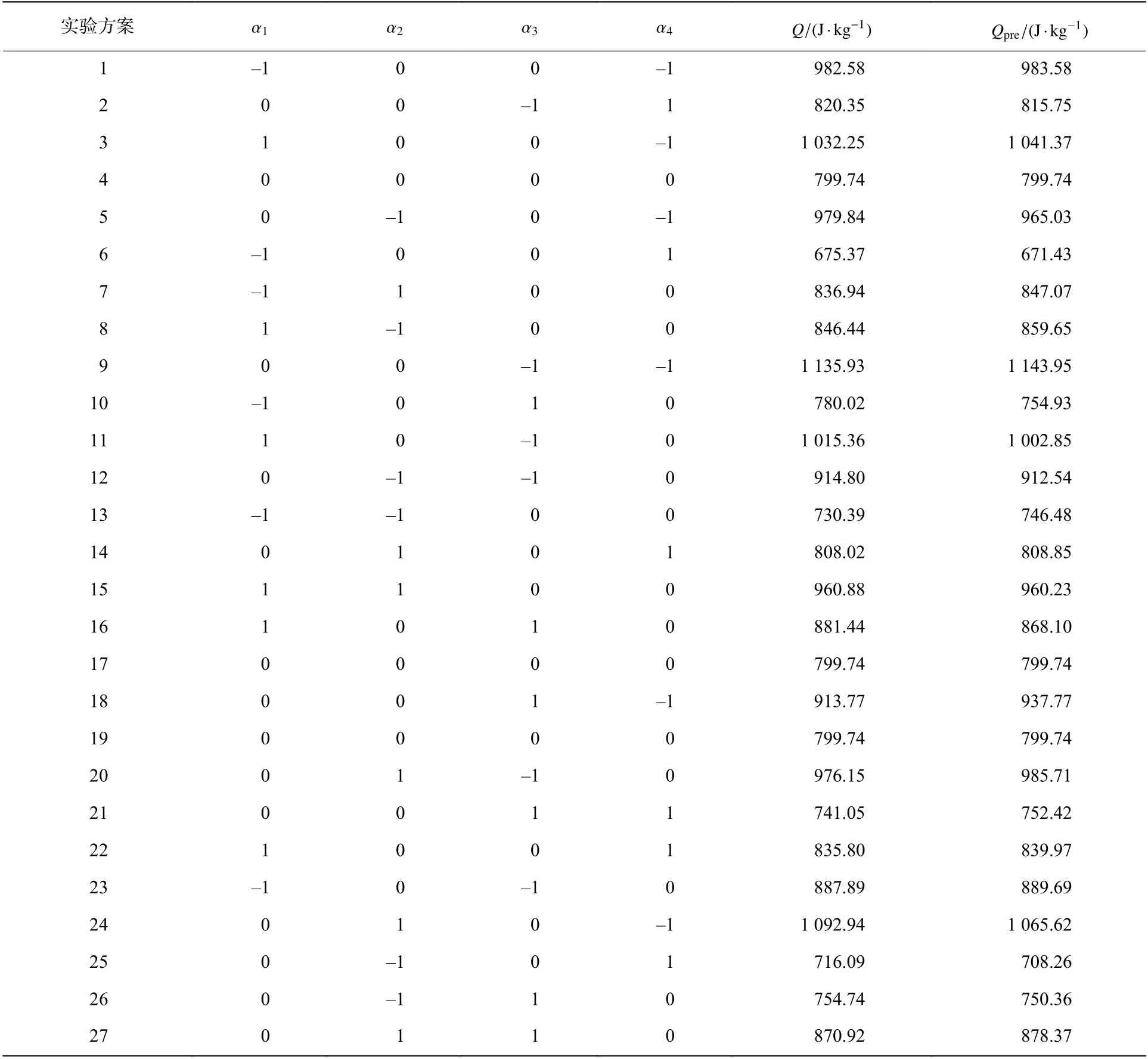
表8 BBD 实验设计Table 8 Experimental schemes designed by the BBD method

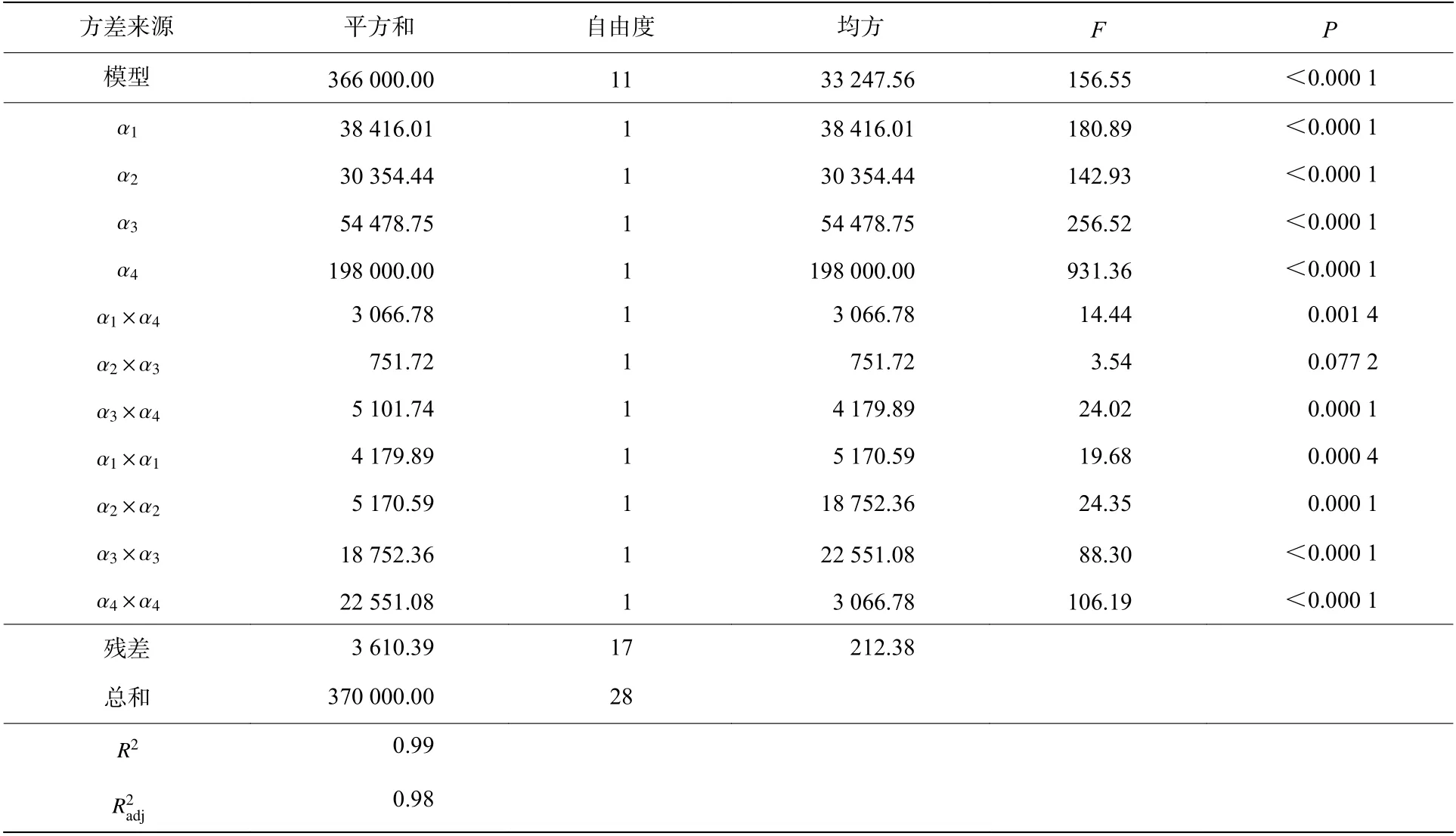
表9 方差分析和参数估计Table 9 Analysis of variance and parameter estimation

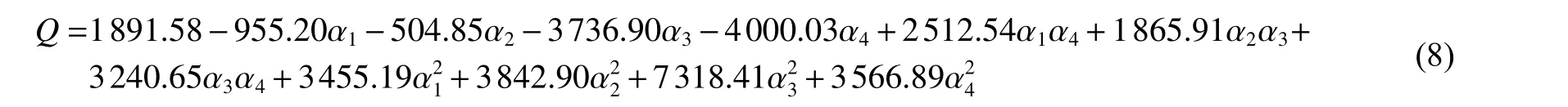
本文中，利用响应面分析法分析了4 个因子之间的相互作用，所得到的响应面方程一定程度上可用于预测模型的比吸能，27 个样本点的预测值如表8 所示。4 个因子对模型比吸能的影响程度最高为 α，其次为 α，再次为 α，影响程度最低为 α。

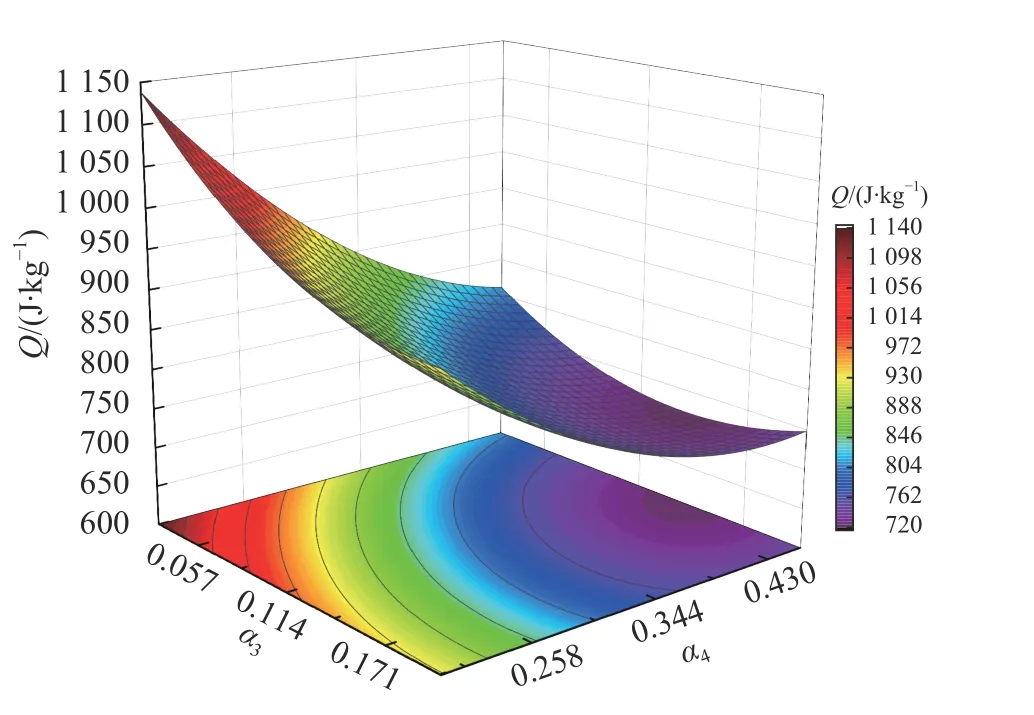
图11 α 3 和 α 4 交互作用对比吸能影响的响应面和等高线Fig. 11 Response surfaces and contour lines of interaction between α 3 and α 4 on specific energy absorption

2.3 遗传算法寻优分析

根据2.2 中所得的响应面方程（式(8)），采用遗传算法进行寻优分析。在保证优化后层合板的总厚度和总质量不超过优化前层合板的前提下，尽可能改善层合板的吸能效果。因此，建立层合板吸能优化数学模型和约束条件：

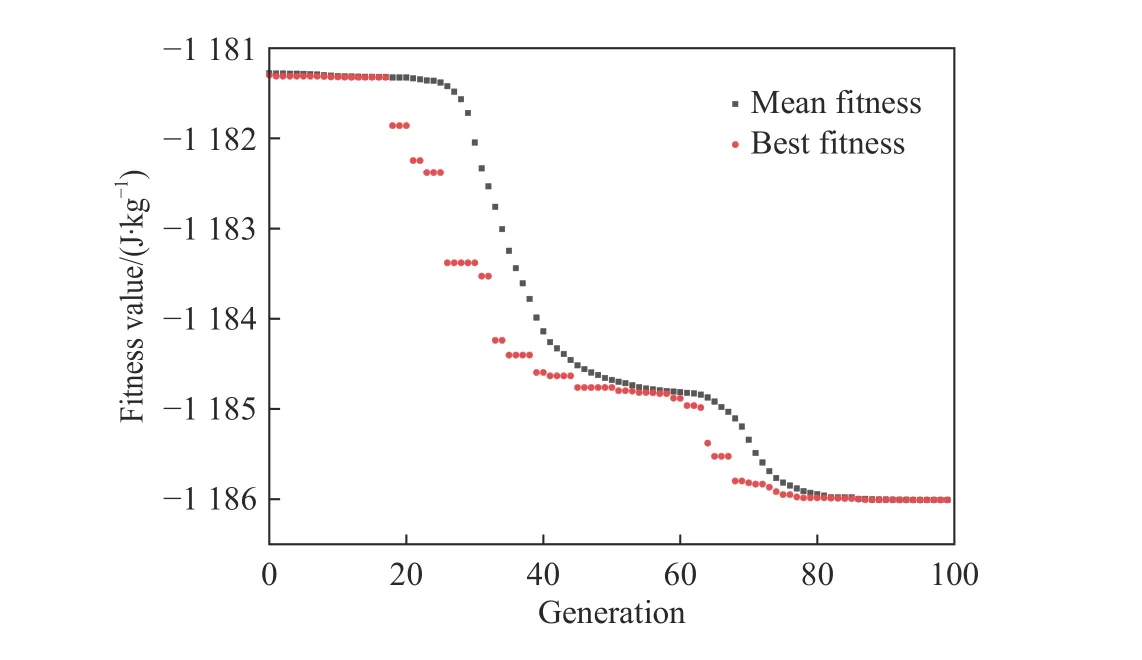
图12 遗传算法寻优过程Fig. 12 Genetic algorithm optimization process

表10 遗传算法优化结果Table 10 Genetic algorithm optimization results

2.4 优化结果验证

根据2.3 节中的优化结果，建立层合板优化方案模型并开展计算分析，优化后的层合板有限元模型如图13 所示。层合板背面板和前面板的最终破坏形式分别如图14～15 所示，层合板产生由弹体圆周向四周扩展的裂纹，为花瓣状。图16 为弹体侵彻层合板过程中各时刻层合板的形态。0.05 ms 时，弹体穿透上层铝薄板，中间层铝板和下层铝板被高速运动的弹体挤压而向外膨胀，发生大变形，纤维层和金属层间发生分层现象。0.10 ms 时，层合板背面板受到拉应力作用，下层铝板出现裂口，随着应力的不断升高，单元不断发生失效和脱落，脱落的单元碎片被弹体的剩余动能冲出靶板背面，随之一起运动。下层铝和纤维层分层范围进一步扩大。0.15 ms 时，弹体即将穿透整个层合板，随着侵彻的深入，层合板裂口不断增大，部分纤维被拔出，层间分层现象更明显。0.20 ms 时，随着靶板材料的破坏和失效，靶板对弹体冲击的抵抗力逐渐减小。最终弹体以一定的剩余速度完全穿透层合板，弹体速度逐渐趋于平稳，惯性力作用后层合板破口面积趋于稳定。

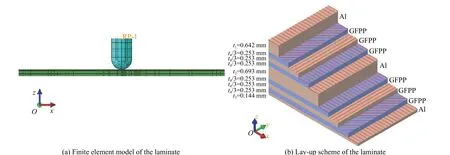
图13 优化后层合板模型Fig. 13 Optimized laminate model

图14 层合板最终变形模式（背面板）Fig. 14 Final deformation mode of laminates (back plate)

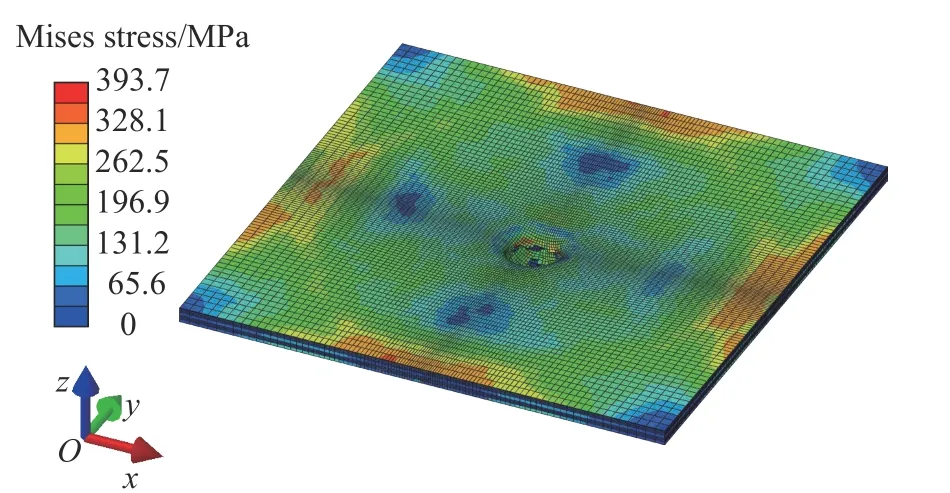
图15 层合板最终变形模式（前面板）Fig. 15 Final deformation mode of laminates (front plate)

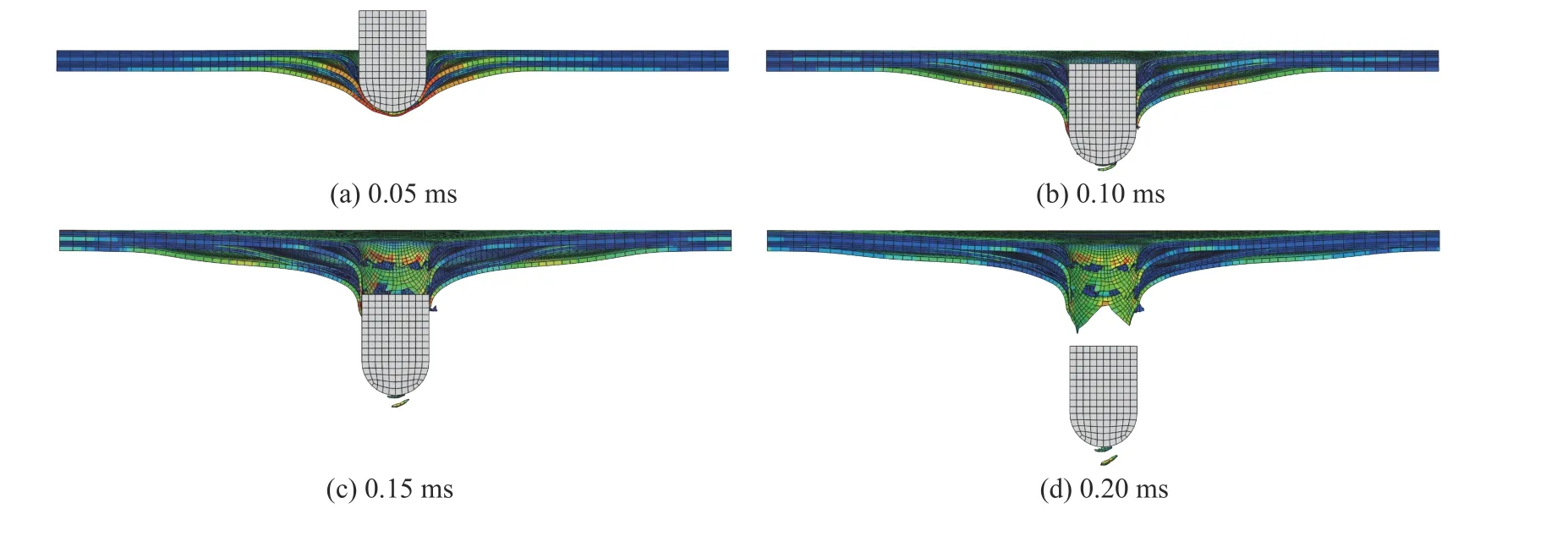
图16 弹体侵彻层合板过程Fig. 16 Process of a projectile penetrating laminated plates

计算得到优化后的层合板比吸能为1 192.66 J/kg，与遗传算法求得的优化解误差为0.56%，说明响应面设计方法是可行的。如表11 所示，优化后的层合板总厚度=3 mm，总质量为69.50 g，抗弹吸能为82.89 J。与初始方案层合板相比，厚度减小了14.30 %，质量减小了11.70 %，吸能增加了19.40 %，优化前后层合板吸能效果对比如图17 所示。

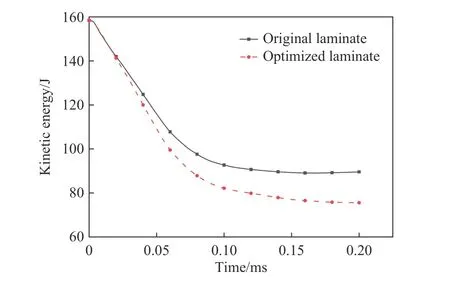
图17 优化前后层合板吸能效果Fig. 17 Energy absorption effect of original and optimized laminates

表11 优化前后层合板主要参数Table 11 The main parameters of original and optimized laminates

3 结 论

利用ABAQUS 进行参数化建模分析，结合多组有限元分析样本，通过响应面算法对铺层形式为A3G23 的纤维金属层合板进行优化设计，得到以下结论。

（1）A3G23 层合板在不同纤维铺层方向下的吸能效果略微存在差异。其中，当采取的铺层方向为Al/45°/90°/0°/Al/0°/90°/45°/Al 时，层合板吸能效果最佳。比较12 种不同铺层顺序方案下的层合板吸能效果，不难发现，层合板最外层铺层方向优先采取45°，层合板最内层铺层方向优先采取0°。

（2）A3G23 层合板中金属层和纤维层的厚度分布对吸能效果有显著影响。根据响应面分析结果可知，4 个因子中，纤维层厚度 α对比吸能的影响程度最高，上层铝厚度 α影响程度较其他因子低。就因子间相互作用而言，上层铝厚度 α和下层铝厚度α分别与纤维层厚度α之间的相互作用显著。当纤维厚度 α取值在中、低、高任一水平时，下层铝厚度 α增大会提高层合板的比吸能，上层铝厚度 α增大会显著降低层合板的比吸能。

（3）较薄的上层铝板、较厚的中间层和下层铝板可以提高抗弹性能，优化后的层合板在弹体的冲击下，下层铝板和纤维间分层更明显，也进一步体现更大吸能的结果。

（4）优化后的层合板比吸能为1 192.66 J/kg，较优化前的抗弹性能有明显提高。层合板厚度减小了14.30 %，质量减小了11.70 %，吸能增加了19.40 %。响应面优化模型比较理想，可为A3G23 层合板的铺层设计提供一定依据。