[100]LiF 单晶在60 GPa 以内冲击加载下的高压屈服强度特性*

谭 叶，李雪梅，俞宇颖，南小龙，甘元超，叶想平，胡建波，王倩男

（中国工程物理研究院流体物理研究所冲击波物理与爆轰物理重点实验室，四川 绵阳 621999）

材料高压高应变率冲击响应特性作为冲击波物理的重要研究内容，往往借助于速度剖面测量进行诊断和分析。加窗测量由于可以有效减弱自由面波反射的影响，对于获取波形畸变尽可能小的速度剖面十分重要，在高压强度、冲击相变、熔化等研究中发挥了重要作用。这时，样品内原位波剖面反演依赖于光学窗口自身的冲击特性参数，需要分别描述其应力球量（）和偏量（）特性的状态方程和本构方程，后者特指描述材料屈服强度特性的函数，如SCG 模型、PTW 模型等。然而，当前相关研究在进行原位波剖面反演时往往忽略光学窗口的强度特性，而只采用状态方程近似描述其应力状态。这种流体近似处理在数百万大气压的高压区是合理的，但在光学窗口尚具有抗剪切能力的中低压力区将导致数据反演精度降低。以氟化锂（LiF）窗口为例，忽略其强度特性可能导致待测材料屈服强度偏离～10%，这对于精密实验是不可忽略的影响。另外，笔者在Sn 相变特性研究中也发现，LiF 窗口屈服强度差异可导致锡相变特征拐点相差～60 m/s。

LiF 单晶由于波阻抗适中、光学透明压力范围宽（冲击：～210 GPa；准等熵：～800 GPa)等优点，是最常用的光学窗口材料。针对LiF 冲击特性已有较多报道，但集中于光学特性、状态方程10,、弹性波衰减及塑性变形机理，高压强度特性研究十分缺乏。Ao 等对[100]LiF 单晶开展了磁驱准等熵加载屈服强度特性研究，发现在5～114 GPa 范围内其强度随压力提高而显著提高，最高至5 倍常压值。Brown 等也对10 GPa 以内磁驱加载下[100]LiF 的屈服强度进行过实验测量。而材料高压强度具有显著的路径相关性，目前尚未见到平面冲击加载下LiF 强度特性的文献报道。

本文中，利用平面撞击技术对～60 GPa 压力内[100]LiF 的强度特性开展系统的实验研究，获得平面冲击加载下LiF 屈服强度随压力的变化规律，确定可描述冲击加载[100]LiF 强度特性的本构模型和参数，比较分析冲击和准等熵2 种加载路径下的强度差异，以期为LiF 窗口在材料本构关系和冲击相变等精密实验中的应用提供重要支撑。

1 实验原理和方法

[100]LiF 单晶在22 GPa 以内冲击加载下具有弹塑性双波响应。为了尽可能减小弹塑性双波导致的复杂波系干扰，提高强度测量精度，采用图1(d)所示的“正碰+LiF 台阶样品布局+LiF 窗口”方式开展冲击-卸载、冲击-再加载速度剖面测量，图中DPS 为多普勒探针系统（Doppler pins system）。这时，由于样品/窗口界面无波反射（波阻抗相同），弹性前驱波不会对塑性冲击波及追赶卸载/再加载波造成干扰而引起速度剖面畸变，实测界面速度即为样品原位粒子速度，由台阶样品的实测界面速度剖面和拉氏分析方法即可准确反演沿卸载（再加载）路径的声速（）-原位粒子速度（）剖面，而无需考虑波直线弯曲和飞片冲击参数的影响。在LiF 为单波响应的更高压力区，也可采用LiF 飞片撞击LiF 窗口的反碰方式。由于LiF 单晶波阻抗低、脆性大，以上述正碰方式为主，在低压区可排除弹塑性双波影响，在单波压力区可以降低弹速要求，从而避免高弹速反碰时LiF 飞片出现损伤而导致的界面速度剖面测量失效。

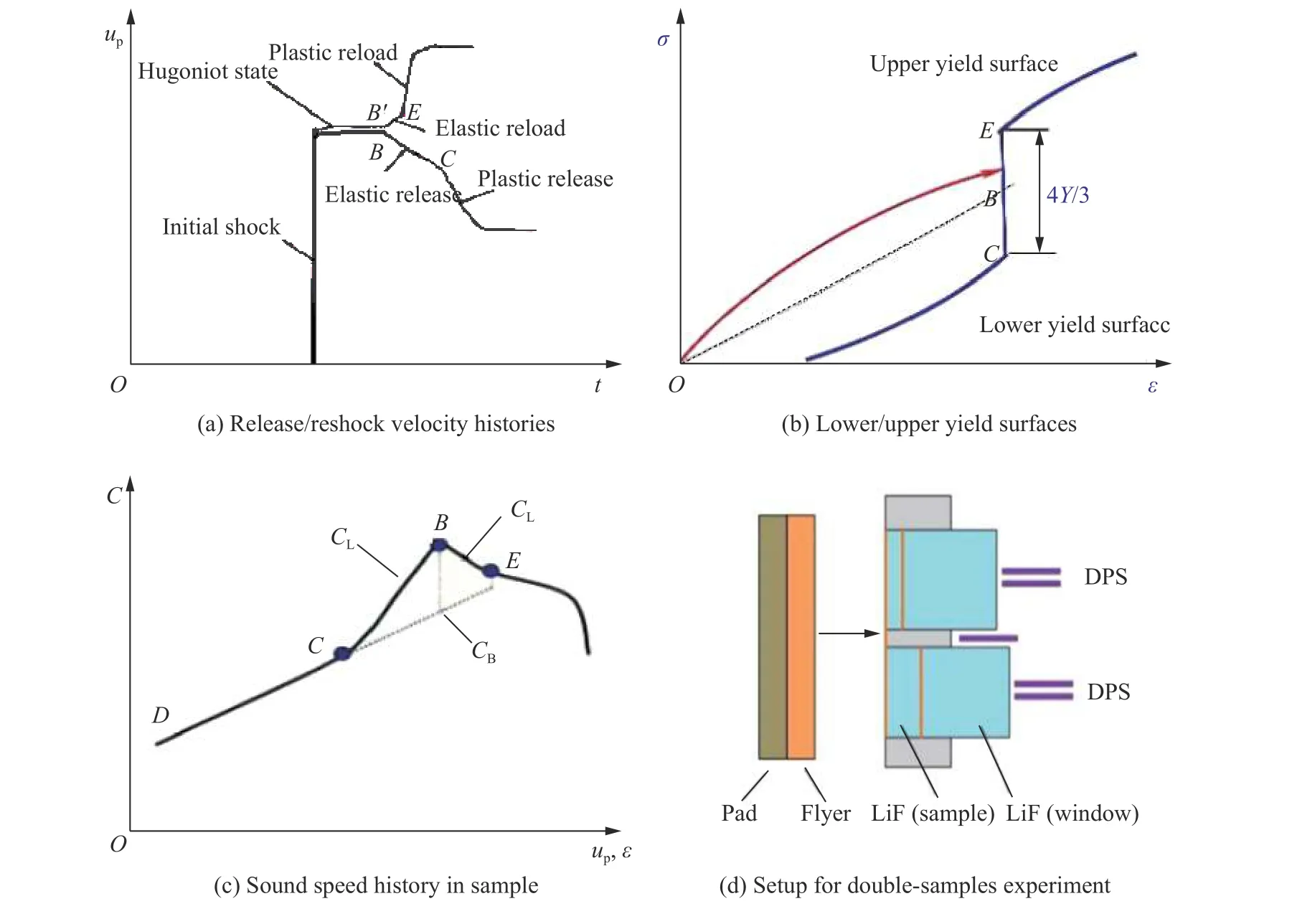
图1 冲击加载下双屈服面法强度测量基本原理Fig. 1 Schematic illumination for the Asay self-consistent method of strength determination

2 实验基本参数

共开展60 GPa 以内6 个压力点的平面冲击加载LiF 强度测量实验。除=32.8 GPa 的压力点只进行了冲击-卸载实验外，其余压力点均包括冲击-卸载和冲击-再加载实验各1 发，基本参数见表1。表1 中PC 为聚碳酸酯（polycarbonate），OFHC 为无氧铜（oxygen free high-conductivity copper）；为飞片速度，即弹速，为飞片厚度，为LiF 样品厚度；实验S-09 中无配对的相近弹速再加载实验， (τ−τ)以实验S-06和S-08 的线性外插值（0.35 GPa）近似；实验S-11 和S-12 为反碰实验，其余为正碰；压力取同一组配对冲击-卸载、冲击再加载实验的平均值。实验采用火炮/气炮加载技术，以双台阶样品正碰为主，无氧铜飞片（＜10 GPa 时飞片材料为-切石英）以预定弹速撞击由[100]LiF 台阶样品和[100]LiF 窗口组成的物理靶，飞片、LiF 台阶样品直径分别为56 和26 mm；第1 块LiF 样品厚度=0（碰靶面），以增大台阶样品厚度差从而提高声速测量精度。反碰实验的飞片和物理靶均为[100]LiF，直径为28 mm。飞片和样品尺寸可确保不小于500 ns 的界面速度剖面平台，且卸载/再加载段主体不受边侧稀疏影响。卸载或再加载追赶波则通过飞片背面的低阻抗或高阻抗衬垫分别引入。[100]LiF 单晶纯度高于99.99%，常态密度为2.638 g/cm，抽样超声测量得到的常压纵波声速为6.643 km/s、横波声速为5.143 km/s。

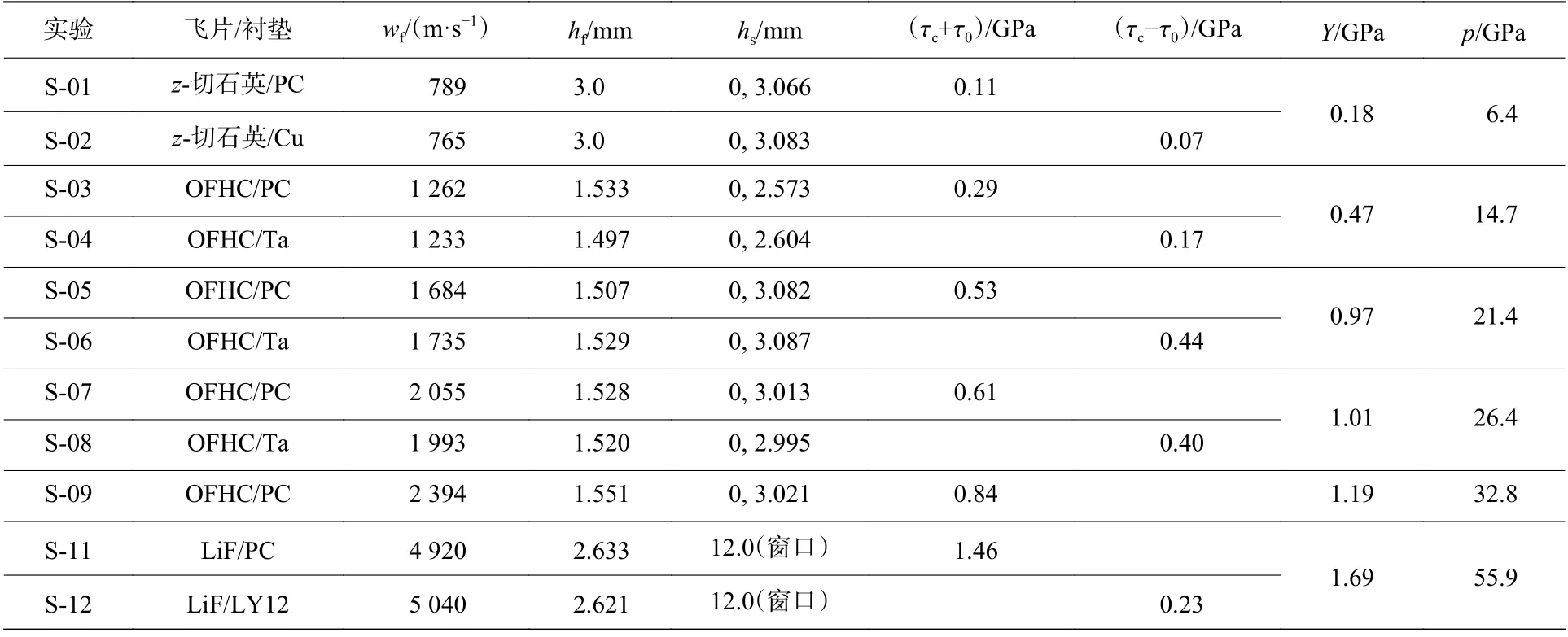
表1 主要实验参数及结果Table 1 Main experimental parameters and results

实验中采用激光干涉测速技术DISAR (displacement interferometer system for any reflector)测量LiF 样品/LiF 窗口界面速度剖面。由于正碰实验的第1 块样品测试面以及反碰实验的测试面为飞片/LiF 窗口界面，为了防止碰靶时窗口表面微损伤引起的光学不透明或透明性下降，LiF 窗口的碰靶面采用了贴Al 箔（厚约8 µm）工艺，以确保飞片/LiF 窗口界面速度干涉条纹信号的有效获取。而样品/窗口界面则通过在LiF 窗口测试面镀Al 膜（厚约1 µm）的方式提高其反光性能，以获取高信噪比的界面速度干涉条纹信号。

3 实验结果与分析

不同加载压力下测得的LiF 双台阶样品/LiF 窗口界面（样品厚度(=0),）的典型原位粒子速度剖面如图2～4 所示，其中由于窗口折射率效应引起的速度修正采用文献[10]给出的公式进行。最高压力点（55.9 GPa）实验数据由二级轻气炮反碰加载获得，由于弹速较高，速度剖面质量略差，主要是由高弹速发射时脆性LiF 飞片内部出现局部非均匀损伤所致。其余几个压力点均采用正碰方式，由于相同压力下正碰加载所需弹速显著降低，实验采用碰靶姿态较优的火炮作为加载平台，速度剖面质量整体较优，LiF 样品/窗口界面准弹性卸载/再加载特征信号明显，再加载信号前端未出现飞片局部脱开引起的非预期速度回跳，确保了完备双屈服面法框架下LiF 屈服强度的求取。

在图2～4 所示的正碰实验中，利用飞片/LiF窗口界面（样品厚度=0）、LiF 样品/LiF 窗口界面（样品厚度）的实测粒子速度剖面，由下式：

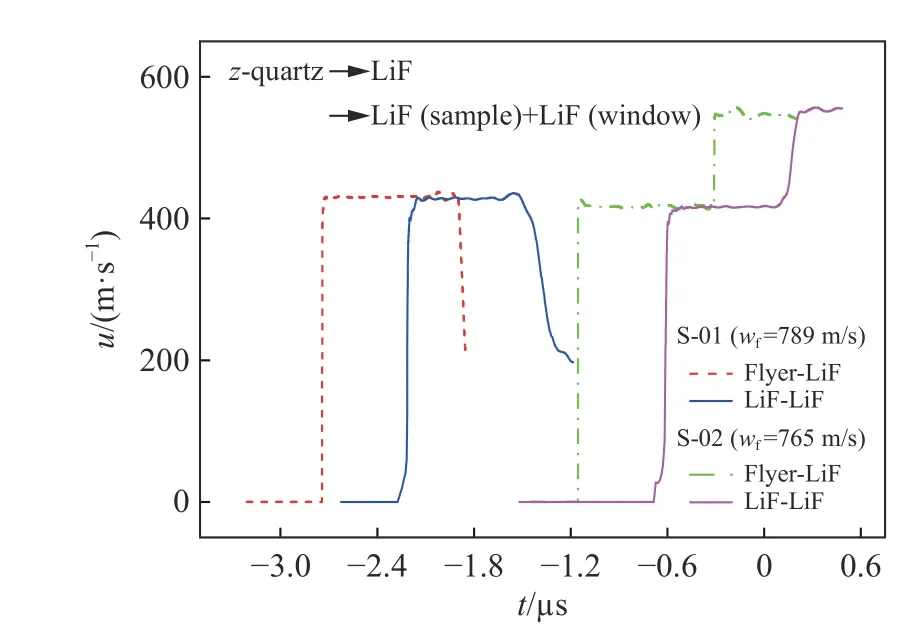
图2 典型的LiF 样品卸载、再加载界面速度剖面测量结果（p=6.4 GPa，z-切石英飞片）Fig. 2 Typical release/reshock velocity profiles measured at the sample-window interfaces for [100] LiF(p=6.4 GPa, z-quartz flyer)

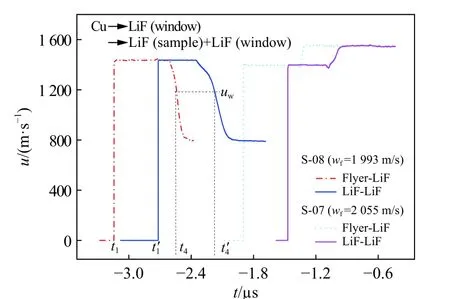
图3 典型的LiF 样品卸载、再加载界面速度剖面测量结果（p=26.4 GPa, Cu 飞片）Fig. 3 Typical release/reshock velocity profiles measured at the sample-window interfaces for [100] LiF(p=26.4 GPa, Cu flyer)

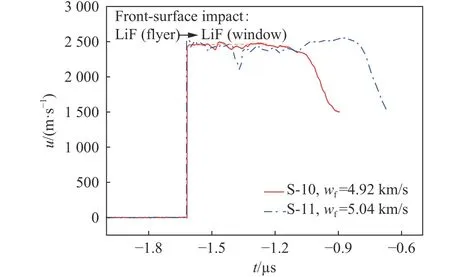
图4 典型的LiF 样品卸载、再加载界面速度剖面测量结果（p=55.9 GPa, LiF 飞片）Fig. 4 Typical release/reshock velocity profiles measured at the sample-window interface for [100] LiF (p=55.9 GPa, LiF flyer)

利用上述分析方法对实测台阶样品（反碰时方法较简单，故略）的界面速度剖面进行数据反演，可获得声速-原位粒子速度曲线（-），详见图5(a)。在本文实验压力范围内，全部-曲线均有显著的准弹性特征；卸载进入下屈服面后，各曲线体波声速的走势基本一致，与理论近似线（点画线，≈+2λ）偏离较小。32.8 GPa 压力点由于仅有冲击-卸载速度剖面，(τ−τ)以21.4 和26.4 GPa 等2 个压力点的线性外插值（0.35 GPa）近似，在图5(b)中以空心“○”表示，得到的值以空心“□”表示。

图5 数据反演获得的[100]LiF 声速-原位粒子速度曲线及屈服强度-压力关系Fig. 5 Sound speed-in-situ particle velocity profiles and pressure dependence of strengths for [100] LiF educed from experimental data

整体看来，冲击加载下，[100]LiF 单晶在～60 GPa 压力范围内仍维持显著的固体强度特性，屈服强度随压力提高而显著提高，强度效应不可忽视。另外，在该压力范围内，(τ−τ)均显著大于零，若仅以卸载实验求取屈服强度而忽略τ与τ的差异将导致屈服强度偏低（=2τ＞τ+τ），而本文完备的冲击-卸载、冲击-再加载实验数据获取显著地提升了双屈服面法强度测量的准确性。

将本文冲击加载[100]LiF 屈服强度数据与文献[18-19]给出的磁驱准等熵加载数据进行汇总比较，如图6 所示。尽管磁驱数据存在一定的分散性，但整体看来，在～60 GPa 压力范围内，冲击加载下的[100]LiF屈服强度高于磁驱准等熵加载结果。

材料高压屈服强度与加载条件、材料微结构均密切相关。加载条件方面，应变率、压力、温度是影响材料屈服强度特性的重要因素。从加载应变率来看，文献[18-19]中的磁驱加载平均应变率为1×10～5×10s，低于本文平面冲击加载（加载前沿～10s）；相应地，磁驱加载时材料的温升较小，冲击加载的温升较高。从图6 给出的2 种加载路径下[100]LiF 屈服强度差异来看，若排除材料微结构差异，则在本文加载压力范围内，[100]LiF 的应变率硬化效应更明显，而温升引入的软化效应相对较弱。

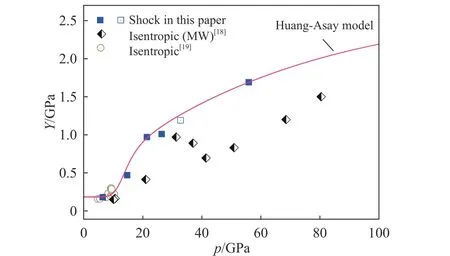
图6 不同加载路径下[100]LiF 的屈服强度比较Fig. 6 Comparison of yield strengths between planar shock and isentropic loading for [100] LiF

暂不考虑应变率因素，采用下式：

从图6 可以看出，方程(4)可较好地对本文的冲击加载LiF 强度特性进行描述。但由于未考虑应变率效应，尚无法用同一套参数对磁驱准等熵加载数据进行统一描述。另外，本文在30～60 GPa 压力范围内的数据点偏少，由此获得的冲击加载下LiF 屈服强度随压力的变化规律还是初步的，更准确地表征有待更多实验数据支撑。此外，后续工作将进一步补充复杂路径实验数据，深入分析压力、应变率、温度对[100]LiF 强度特性的影响规律，为适用性更强的高压-高应变率本构模型研制提供支撑。

4 小 结

利用平板碰撞和双屈服面法，结合原位剖面测量技术，获得了60 GPa 以内冲击加载下典型光学窗口材料[100]LiF 屈服强度随压力的变化规律，分析了冲击加载和磁驱准等熵加载2 种不同路径下的LiF 屈服强度特性差异，得到主要结论如下：

（1）在～60 GPa 压力范围内，[100]LiF 具有明显的抗剪切变形能力，屈服强度随加载压力提高而显著提高，压力硬化效应明显；

（2）相同压力时，冲击加载下的LiF 屈服强度高于磁驱准等熵加载，在～60 GPa 压力范围内应变率硬化效应占主导，温度软化效应相对较弱；

（3）采用以SCG 模型为基础的Huang-Asay 本构模型可较好地描述本文冲击加载下的LiF 强度特性，并由此确定了模型参数。

LiF 在实际应用中往往被作为冲击实验的光学窗口使用。本文结果为LiF 窗口在材料本构关系和冲击相变等精密实验中的应用提供了重要支撑，数据反演时通过加入LiF 窗口自身的本构模型，可以排除窗口强度效应的影响，提高非透明样品内部的本构响应、相转变等数据的反演精度。后续工作拟补充开展基于阻抗梯度飞片提供的复杂可控路径加载强度实验，进一步比较不同加载路径下[100]LiF 的屈服强度特性，深入分析压力、应变率、温度对其强度特性的影响规律，为适用性更强的高压-高应变率本构模型研制提供更丰富的基础实验数据。