轴类间隙内摩擦损失模型验证及流动特性分析
2022-05-21邓清华胡乐豪赵奕萌杨国英李军丰镇平
以透平、电机为代表的旋转机械在工作中不可避免地产生各种损失
,一方面,损失降低能量转换效率,另一方面,损失最终转换成热量使相关部件温度升高,给设备的高效和安全运行带来严重问题
。因此,旋转机械中的损失是研究热点之一。
旋转机械由静子和转子构成,为避免动静碰摩,静子和转子之间会预留一定间隙。通常情况下,间隙内会充满流体,当转子旋转时运动的转子与流体之间发生相对运动,产生摩擦损失,消耗机械能。
研究表明,在大型低速且工质压力不高的旋转机械内,摩擦损失通常可忽略不计。在小型高转速旋转机械内,尤其当工质压力较高时,摩擦损失则成为了损失的主要来源,在美国桑迪亚国家实验室设计的超临界二氧化碳(sCO
)高速原理样机中,摩擦损失约占总损失的37.5%
。
人之生也柔弱,其死也坚强。 万物草木之生也柔脆,其死也枯槁。 故坚强者死之徒,柔弱者生之徒。 是以兵强则不胜,木强则兵。 强大处下,柔弱处上。
实际上,早在20世纪就有学者对间隙内的摩擦损失进行实验测量,并在此基础上提出预测摩擦损失的模型。目前,常见的摩擦损失模型有4种
:Wendt、Bilgen等分别提出了适用于光滑壁面的摩擦损失模型,其模型同时考虑了流动状态和泰勒涡的影响;Vrancik、Yamada等在理论和实验研究基础上也分别提出了摩擦损失模型,与Wendt和Bilgen模型不同的是,这两种模型仅考虑了流动状态影响。需要指出的是,虽然以上4种损失模型均是基于实验结果得出,但是对于同一工况,有些损失模型的预测结果偏差远超过了工程可接受的程度,实际无法应用。Saari对电机间隙内的摩擦损失进行了实验研究,并将实验结果与Bilgen提出的摩擦损失模型的预测结果进行了比较,模型预测结果与实验结果的偏差较小
。
近几十年来,诸多研究者采用数值方法开展了间隙流动特性与摩擦损失的研究。2002年,刘难生等通过对三维不可压缩Navier-Stokes方程进行离散,数值模拟两个同心圆柱间隙内的流动,研究间隙内流场细节,预测流动失稳时的临界雷诺数
,该研究初步探明了Taylor-Couette(TC)流动机理及其发展过程,但是未对于高雷诺数下的流动特性进行分析。2014年,杜珩等采用直接数值模拟方法,研究了在不同间隙宽度时间隙内的流动状态,结果表明随着间隙宽度增加,泰勒涡对流动脉动特性贡献增大
,但该研究仅关注大尺度泰勒涡运动对流动的影响,没有阐明小尺度涡的影响机理。
2018年,Liu等对不同电机结构的摩擦损失的研究结果表明,电极上增加围带可减小间隙内的摩擦损失
。同年,Anderson等采用数值方法研究电机进出口效应及流动非定常性对摩擦损失的影响,发现泰勒涡的形成与发展受雷诺数的影响较大
。需要指出的是,Liu和Anderson在以电机为研究对象时考虑了流体轴向速度,间隙内流动为Poiseuille-Couette-Taylor(PTC)流动,摩擦损失也因此受到了影响。
近年来,sCO
循环及其动力部件的发展非常迅速
,研究发现在小型高转速机械中,sCO
的摩擦损失比空气的摩擦损失高出数十倍。因此,对sCO
摩擦损失的研究成为新的热点之一。2019年,蒋宇对sCO
原理样机中的摩擦损失进行了数值计算,发现sCO
的摩擦损失主要与转子转速有关
。2020年,梁腾和等研究了间隙内sCO
的摩擦损失及流动特性,研究发现当间隙内sCO
压力较大时,转子表面粗糙度对摩擦损失的影响较大,常见的损失模型已无法准确预测摩擦损失
。
在以往研究中,对于常见的摩擦损失模型缺乏全面系统地验证与校核,且间隙内的流动特性与损失关系也未明晰。因此,本文针对转轴和壳体形成的轴类间隙,数值验证文献[6]的摩擦损失模型,分析了间隙内流动状态对摩擦损失的影响,为高速电机和叶轮机械设计过程中摩擦损失模型的选择提供依据,同时为完善或发展新的摩擦损失模型提供了参考。
1 摩擦损失
前人的理论研究结果表明,摩擦损失与间隙内流动状态、工质密度
、间隙内径
、线速度
以及间隙长度
有关,具体的计算公式如下
=
π
(1)
式中
为表面摩擦系数。
当间隙内流动为层流时,可以通过理论分析,推导出表面摩擦系数
的计算公式为
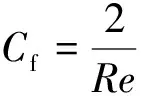
(2)
式中雷诺数
定义如下

(3)
其中
为工质的动力黏度,特征长度取间隙宽度
,特征速度取线速度
。
2.误填基本建设支出经费。如把学校所有的基本建设支出填入“基本建设支出”。基本建设支出是反映各级发展与改革部门集中安排的公共财政预算(不包括政府性基金以及各类拼盘自筹资金等)用于购置固定资产、土地和无形资产,以及购建基础设施、大型修缮所发生的支出。学校的基本建设大部分是使用事业收入来安排建设的。
本文采用ANSYS Fluent对流场进行定常数值模拟,其物性数据来自NIST Refprop物性库,流体域的剖分采用结构化网格。
=
(4)
式中
、
、
为常数,一般由实验确定。

(5)
当间隙内流动为湍流时,表面摩擦系数
的计算公式依赖于实验总结出的经验公式,表1给出了常用的表面摩擦系数
的计算公式。
为确定多港口地区港口投资的均衡,需确定投资人的投资收益函数以及投资策略空间,并模拟港口投资之间的投资博弈行为。

从表1中可以看出,模型1、模型3的表面摩擦系数
仅为
的函数,而模型2、模型4的表面摩擦系数
与
、结构参数
均有关,这实际上是损失模型的构建方法不同导致的。
模型1假设间隙内速度在湍流状态下满足底数为e的对数分布

(6)
本文模型的主要几何尺寸如表2所示。表3是本文数值计算的边界条件,工质为空气,用于开展湍流模型和网格无关性验证、摩擦损失及流动分析等研究。端壁、静子壁面均设置为静止无滑移壁面,转子壁面为旋转无滑移壁面。需要指出,文献[11]的线速度范围为156~233 m/s,本文为了验证结果更具适用性,数值计算的线速度范围为74~233 m/s,其他边界条件与文献[11]相同。
=
2;
=
2
(7)
将式(7)代入式(6),可得

(8)
式中:(
)
为表面摩擦系数
;
、
分别为1.633、0.884。
模型3的构建方法与模型1基本相同,只是其假设间隙内速度满足底数为10的对数分布,
、
分别为5.5、5.75。
模型2和模型4的构建方法基本相同。在实验数据基础上发现摩擦损失主要与结构参数
和流动参数
有关,拟合出了摩擦损失模型的经验公式
主要考察了政府会计制度的改革以及国家会计制度改革对事业单位现有财务管理的影响,旨在促进未来治理制度和公共财务管理的某些改革。发现我国公用事业会计系统存在的一些问题,如会计核算和登记等系统管理不够规范,制度内容不健全等。在现行的会计和预算管理系统中,原有财务系统并不能反映该机构的实际情况。制度核算体制改革至关重要,会计制度改革是一项长期任务。目前,事业单位会计制度改革后,可以更有效地改善事业单位会计制度,大大提高事业单位的经济管理和资产管理,同时提高事业单位的办事效率。
=
-
(9)
其中结构参数
定义为
4.药物浓度检测:特殊人群如儿童、妊娠妇女及肾功能不全患者等用药在条件允许情况下可进行治疗药物浓度监测(TDM)。
2 几何模型及数值方法校核
2.1 几何模型
芬兰赫尔辛基理工大学(HUT)以空气为工质实验研究了转子转速对摩擦损失的影响
,HUT流体域几何模型如图1所示,静子壁面、转子壁面以及两侧端壁组成了封闭的流体区域,且所有壁面均为水力光滑壁面。

式中:
为当地速度;
为摩擦速度;
、
均为经验系数,由实验获得;
为当地径向位置。由于忽略了间隙的曲率对流动状态的影响,因此认为当地速度为间隙中间处的速度,即


2.2 数值方法验证
另外,本文分析中用到的泰勒数,反映了离心力与黏性力对流动状态的影响,定义如下
2.2.1 湍流模型验证
湍流模型一般分为基于Bossinesq假设的涡黏性模型和雷诺应力模型。常见的
-
模型和
-
模型均属于涡黏性模型,其优点是避免了对雷诺应力项的直接求解,计算量小,缺点是在强旋转、大曲率、外受力场作用较强的流场中,其计算精度低。雷诺应力模型直接建立雷诺应力的输运方程,其优点是考虑了旋流和流向表面曲率变化的影响,缺点是需要求解更多数量的方程,计算量大。
本节湍流模型验证基于HUT几何模型,网格数为308万,静子内表面的第一层网格高度为5.0 μm,网格增长率为1.1,径向网格层数为15。
本文采用
-
模型、
-
模型、SST模型和雷诺应力(RSM)模型4种湍流模型进行验证,湍流模型的验证结果如图2所示,可以看出,RSM模型与实验结果最为接近。另外,在本文的计算域中,间隙宽度较小,当转子旋转时间隙内会产生不稳定流动,常见的
-
模型和
-
模型无法对间隙内流场进行准确、细致地刻画,而雷诺应力模型则对不稳定流动的求解具有更高的精度。综合以上考虑,本文选取RSM模型进行计算。

2.2.2 速度分布验证
鉴于各水库工程的成本费用和所在地区经济发展水平、水资源紧缺程度各有不同的实际,按照“分期实施、逐步到位”和“区域基本同价”的原则,建议对30座大型水库和各区域典型中型水库工程的城镇供水(原水)价格作出调整。供水价格调整后,各水管单位要努力深化改革,强化内部管理,切实控制成本,降低费用,完善计量方式和水费使用办法,规范成本核算,实现良好的经营管理以促进水利行业发展。
2.2.1小节通过不同湍流模型验证了摩擦损失大小,本节为进一步验证RSM模型捕捉的流场细节,将计算流体动力学(CFD)数值计算结果与Adebayo等
采用粒子图像测速技术的实验测量结果进行比较,如图3所示。
教师对课堂管理宽松,缺乏互动交流 学生上课使用手机现象普遍,教师会提出口头警告,但有部分教师放任其自由发展,不会对学生课堂使用手机做出硬性要求,不影响正常教学秩序即可,选择性忽略上课使用手机的学生。教师是课堂教学的组织者和管理者,有对学生上课使用手机进行制止的权利。学生在相对宽松的课堂管理下,不会去提前预习,也深知教师并不会刻意去提问,所以不愿与教师、同学进行互动交流,久而久之,上课使用手机与教师课堂管理态度产生关系。
武陵山景区周边也有著名旅游景区,如武隆仙女山、大木花谷等相应也有特色小镇建设的规划,存在区域内的竞争关系。
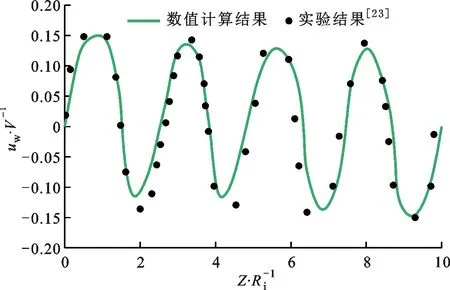
速度分布验证的几何和工况参数与文献[17]保持一致,具体如下:间隙内径为25 mm,间隙外径为57 mm,间隙宽度为32 mm,间隙长度为250 mm,转速为500 r/min;工质为空气,压力为0.101 3 MPa,温度为298.15 K,密度为1.184 0 kg/m
,动力黏度为17.8 μPa·s。数值计算采用结构化网格,湍流模型采用RSM模型,网格参数与2.2.1小节保持一致,网格数为200万。在图3中,横坐标
为轴向坐标,纵坐标
为轴向速度,可以看出,实验测量的速度值与数值计算得到的速度分布基本一致,说明本文采用RSM模型的计算结果是可靠的。
2.2.3 网格无关性验证
为提高网格质量和计算精度,本文针对图1所示的几何模型,采用结构化网格剖分计算域,同时为保证壁面的
能满足要求,对转子、静子的壁面网格进行了加密处理。综合考虑,转子外表面、静子内表面的第一层网格高度为5.0 μm,网格增长率均为1.1,径向网格层数为15,计算域网格如图4所示。

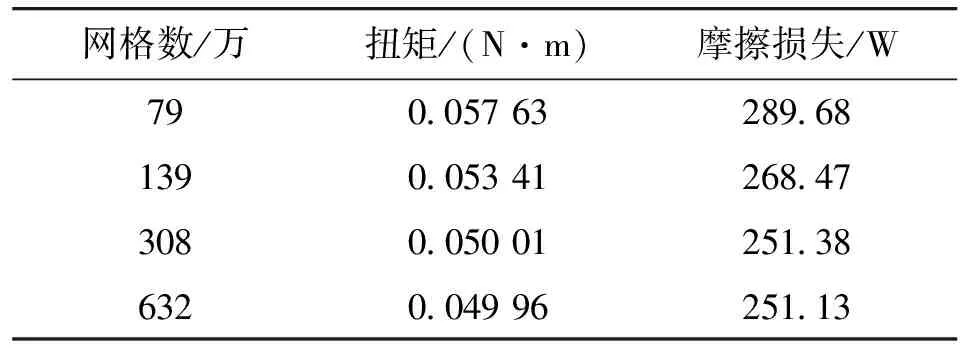
本文采用79万、139万、308万、632万的网格分别进行数值计算,边界条件如表3,转子线速度为178 m/s。表4为网格无关性验证结果。当网格数从308万增加到632万时,间隙内的摩擦损失从251.38 W减小到251.13 W,二者相差0.099%,扭矩数值基本相同。因此,本文选择308万的网格开展间隙内摩擦损失的数值研究。
3 计算结果分析
3.1 不同线速度下损失模型验证及流动分析
本节采用如表3所示的边界条件验证了表1的4种摩擦损失模型,并将数值计算结果与4种损失模型的预测结果进行比较,如图5所示。
婆婆听了我的想法,考虑了一个晚上,最后郑重地告诉我:“孩子,我尊重你的选择,明天我们就去医院检查,如果没什么问题,你就去外地,我跟你去,陪在你身边照顾你!”
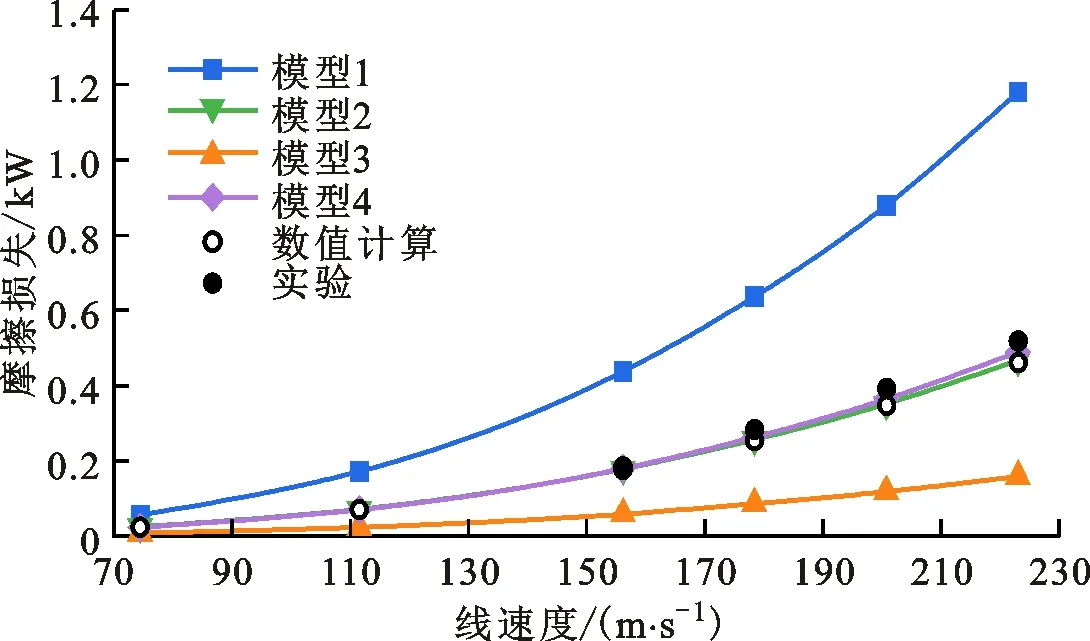
从图5中可以看出,在相同线速度条件下,模型1的预测结果远大于其他3个模型的预测结果,与模型2的最大相对偏差为153%。模型3的预测结果均小于其他模型的预测结果,与模型2的最大相对偏差为-65%。模型4与模型2的计算结果较为接近,两者之间的相对偏差小于10%。
比较数值结果后可以发现,当转子线速度范围在74~233 m/s时,模型2、模型4与数值结果的预测结果较为接近,相对偏差均小于10%,而模型1、模型3的预测结果差异较大,模型1与数值结果的最大相对偏差超过了150%,模型3与数值结果的最大相对偏差均超过200%。需要指出,随着线速度增大,模型2、模型4的预测结果与数值结果的相对偏差增大。当转子线速度为74 m/s时,模型2与数值结果的相对偏差为1.08%,模型4与数值结果的相对偏差为-5.22%;当转子线速度为233 m/s时,模型2与数值结果的相对偏差为1.44%,模型4与数值结果的相对偏差为6.15%。
从式(6)~式(9)可以看出,模型1、模型3在对表面摩擦系数
推导时忽略了间隙曲率的变化,仅考虑了流动状态的影响,而模型2、模型4在拟合公式时考虑了结构参数
影响。实际上,参考式(4)对于
的定义,结构参数
反映流体所受的离心力效应产生的泰勒涡对流动的影响,对于不同的
,泰勒涡对摩擦损失的贡献是不同的,一般而言,随着
增加,泰勒涡对摩擦损失的影响逐渐趋于主导地位。因此,模型1、模型3本质上忽略了间隙内泰勒涡对摩擦损失的影响,从而导致了数值结果与损失模型之间存在较大偏差。
另外,
越大,离心力效应越明显,间隙内更容易产生泰勒涡。研究发现,当
达到1 700~1 800时,间隙内将产生泰勒涡
,此时的
称为临界
。实际上,临界
会受转子半径与静子半径的比值、转子静子温度、间隙内流体的质量流量等因素影响
。
2.2 两组患者术后并发症发生情况比较 B组术后多器官功能障碍综合征(multiple organ dysfunction syndrome,MODS)发生率为2.9%(1/34),显著低于A组的8.3%(2/24),差异有统计学意义(P<0.05)。两组患者PND、短暂神经系统并发症、急性肾损伤、病死率比较,差异均无统计学意义(P>0.05)。
因此,综合数值结果与损失模型预测结果比较及对偏差的分析可以发现,模型2、模型4预测的摩擦损失更符合实际的摩擦损失,同时说明了间隙内泰勒涡对摩擦损失的影响不可忽略。
图6是线速度为74 m/s时间隙内的压力云图。需要指出,图例中的压力是以设定压力(0.101 3 MPa)作为参考压力。另外,由于间隙内的流动具有周期性特点,本文在分析间隙内的流动时主要分析一侧端壁的流动状况。
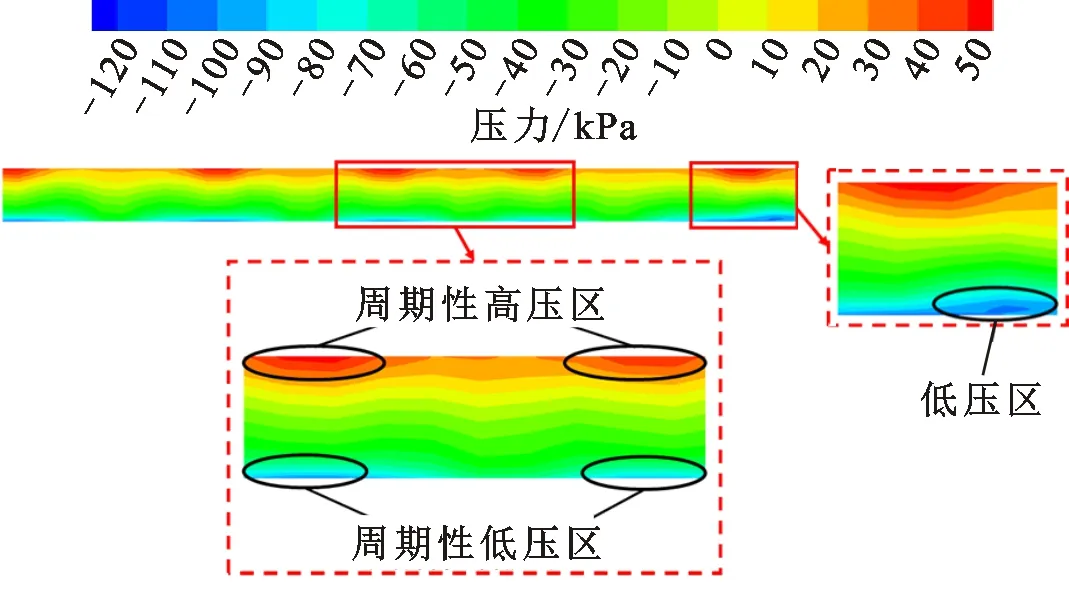
从转子壁面到静子壁面,压力逐渐升高,即转子侧的压力小于静子侧的压力。这是由于流体在转子壁面附近的速度大于在静子壁面附近的速度。另外,在转子和静子壁面附近分别存在周期性的高压区和低压区,并且转子壁面的低压区范围小于静子壁面的高压区范围。这是因为流体在黏性力和离心力共同作用下,间隙内会产生周期性的泰勒涡。
同时,受到静止端壁的影响,转子壁面附近存在一定范围的低压区,这是因为在端壁和转子壁面的共同作用下,流体在转子和端壁附近会产生较大的速度梯度,使该处的压力下降较快,产生明显的低压区。
(4)桥梁施工安全控制,安全是施工的第一要素,同时这也是整个施工过程中最重要的一个因素。所以为了避免可能出现的一些安全隐患及其可能产生的危险现象,必须确保施工的安全性,对施工过程的合理进行也要做出一些相应的措施,坚决避免一些可以预防的危险现象。
图7是不同线速度下间隙内的速度分布。当线速度为74~233 m/s时,整个间隙内都会存在周期性泰勒涡。同时发现,在端壁附近,泰勒涡形状和大小与远离端壁附近泰勒涡不同。这是因为静止端壁对间隙内流动产生影响。

从图7的速度云图中可以看出,流体速度从转子壁面到静子壁面逐渐减小,转子壁面附近的流体的速度与转子速度一致,静子壁面附近流体的速度为0。同时发现,当线速度为74 m/s时,端壁附近的低速区的范围较大,当线速度为233 m/s时,端壁附近的低速区范围明显减小,说明随着线速度增加,壁面附近的低速区的范围在逐渐减小,端壁对流体速度的影响逐渐减小。分析认为,这是因为线速度升高,惯性力对流动的影响增大,黏性力的影响减小,静止端壁对流动的影响逐渐减弱。
犹太人财商教育最重要的一点,是培养孩子延后享受的理念。所谓延后享受,就是指延期满足自己的欲望,以追求自己未来更大的回报,这几乎是犹太人教育的核心,也是犹太人成功的最大秘密。犹太人是如何教育孩子的呢?“如果你喜欢玩,就需要去赚取你的自由时间,这需要良好的教育和学业成绩。然后你可以找到很好的工作,赚到很多钱,等赚到钱以后,你可以玩更长的时间,玩更昂贵的玩具。如果你搞错了顺序,整个系统就不会正常工作,你就只能玩很短的时间,最后的结果是你拥有一些最终会坏掉的便宜玩具,然后你一辈子就得更努力地工作,没有玩具,没有快乐。”这是延后享受的最基本的例子。
图8给出不同线速度时在
=0.5截面上间隙内的平均速度分布,
为径向坐标。从图8可以看出,在不同的线速度下,间隙内速度的径向分布特征基本相同,速度沿径向均被分成转子壁面速度下降区、速度稳定区和静子壁面速度下降区3个区域。可以看出,流体在不同的线速度时速度稳定区的范围基本相同,达到的稳定速度为转子线速度的一半左右。转子和静子壁面附近速度梯度变化剧烈,实际上是由于壁面处的边界层导致的。
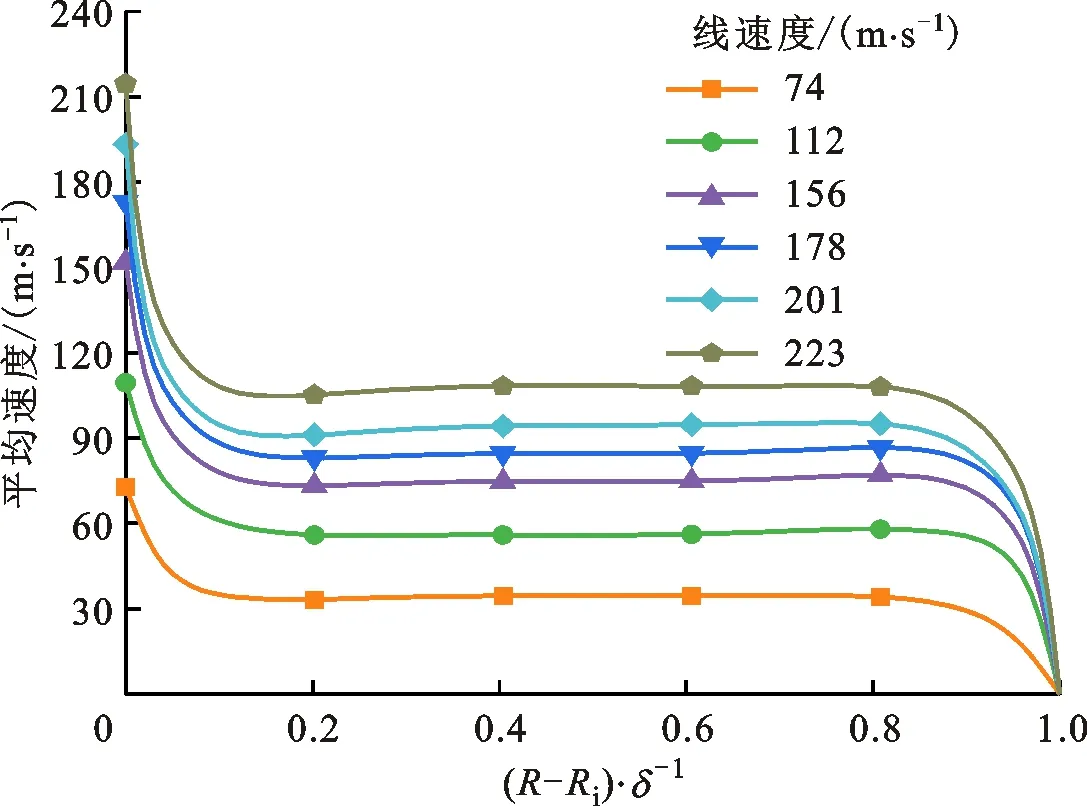
需要指出,随着线速度的升高,流体在转子和静子壁面附近的速度梯度增大。分析认为,转子线速度越大,流体所受的离心力作用越强,黏性力对流动的影响相应减小,因此壁面处的边界层厚度减小,导致边界层内的速度梯度增大。
图9是线速度为74~233 m/s时间隙内的涡量云图。从图9可以看出,转子和静子壁面处的涡量大于中心处涡量,并且沿径向方向,高涡量区和低涡量区有明显界限。这主要是因为壁面处受到边界层影响,流体的速度梯度大于中心处的速度梯度。另外,随着线速度的升高,壁面处的高涡量范围增大,这说明了随着线速度的升高,流体受到离心力的影响越来越显著,间隙内流动不稳定增强,因此间隙内的摩擦损失随线速度的升高而逐渐增大。

3.2 不同密度下损失模型的验证及流动分析
从式(1)可以看出,工质密度对摩擦损失会产生影响,为了全面校核该模型,本节重点研究间隙的摩擦损失随工质密度的变化关系。表5给出了在温度为323.15 K不同空气密度时的计算条件。

图10为不同线速度时摩擦损失随间隙内压力的变化,可以看出,在不同的线速度下,间隙内的摩擦损失随着压力的增加均呈线性增加,这与式(1)显示的摩擦损失与工质密度呈线性关系是一致的。同时,比较图10(a)、10(b)可以发现,在不同线速度下,间隙内的摩擦损失随压力的变化趋势基本相同,并且发现,当线速度为74 m/s和233 m/s时,模型4与数值计算结果较为接近,两者之间的最大相对偏差分别为-5.22%和6.15%,并且相对偏差随着流体压力的增大基本不变。模型1、模型3的相对偏差较大,最大相对偏差超过100%,超过了工程应用允许偏差范围,因此不建议在实际工程中应用。

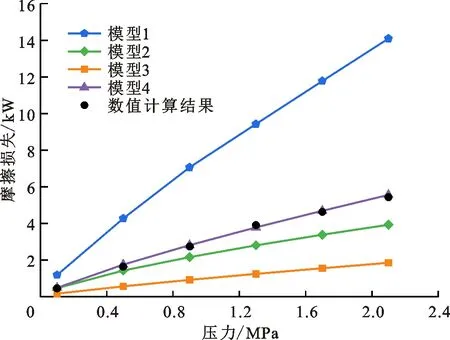
模型2的相对偏差随着流体压力的增加逐渐增大,当流体压力为0.101 3 MPa时,模型2与数值计算结果之间的最大相对偏差为1.44%,但是当流体压力为2.1 MPa时,两者之间的最大相对偏差为-27.60%。实际上,压力对预测精度影响是由于流动雷诺数不同导致的。当10
<
<6×10
时,模型2的预测精度更高,但是当
>6×10
时,模型4的预测精度更高且不受流动状态的影响。当10
<
<6×10
时,模型2采用多项式拟合了结构参数
对表面摩擦系数的影响,相比于模型4的单项式准确性更高。当
>6×10
时,模型2的偏差相对模型4较大,据分析,这主要是在文献[8]的模型2提出过程中,在雷诺数10
~10
范围内,摩擦损失研究的实验工况比文献[10]的模型4偏少,其模型精度受到了一定影响。
图11给出了转子线速度为74 m/s时不同密度下间隙内的速度分布。从图11可以看出,随着间隙内的压力增大,流体密度增大,流体动力黏度基本不变,因此间隙内流动的
增大,导致转子和静子壁面附近边界层的厚度减小。当压力为0.1 MPa时,壁面附近可以看到明显的高速区和低速区。然而,当流体压力为2.1 MPa时,径向方向上的速度梯度较小,壁面附近的高速区和低速区基本消失。

同时,当压力为0.1 MPa时,整个间隙内充满了泰勒涡,但是随着压力增大,泰勒涡在逐渐减少,当压力为2.1 MPa时,整个间隙内流动基本呈单向不稳定流动,流动处于湍流状态。文献[25-26]指出,随着流动的
增大,泰勒涡的形态也会从一般的泰勒涡形状发展为波状泰勒涡、调制波状泰勒涡,最终演化为湍流状态。分析认为,在相同的线速度条件下,即间隙内的工质受到的离心力相同时,随着工质压力增加,流动的雷诺数增加,间隙内流动的不稳定性增强,从而导致泰勒涡结构发生变化,直到最终发展为完全的湍流流动。因此,间隙内的摩擦损失随着流体压力增加而增大,这与图10得出的结论是一致的。需要指出,随着流体压力增大,静止端壁对泰勒涡结构的影响逐渐减小,当压力为2.1 MPa时,端壁附近的泰勒涡结构也基本消失,说明此时间隙内流动主要受到离心力影响,端壁对流动的影响可以忽略不计。
4 结 论
本文基于摩擦损失实验数据,在不同线速度和密度条件下考核了4种摩擦损失模型的预测精度,分析轴类间隙内的流动特性,其主要获得结论如下:
(1)当线速度为74~233 m/s时,模型2、模型4的预测结果与数值结果较为接近,相对偏差均小于10%,模型1、模型3的预测结果与数值结果偏差较大,其最大偏差超出了工程中的允许偏差。随着线速度升高,模型2、模型4预测结果与数值结果的相对偏差增大。
更为关键的是,电商平台直接对接农户做C端,缩短了中间环节、减少了流转费用、节省了利润,溢出的利润与农户分享、使农户收益。“这些电商平台进来农资环节之后,可以提供一整入的种植技术和农业服务,而不仅仅是肥料。相对来说形成了一个封闭体系。”一位企业老总直呼惊出一身冷汗。显然,传统渠道伤不起!
(2)当线速度为74~233 m/s时,整个间隙内都存在周期性泰勒涡。速度沿径向被分成转子壁面速度下降区、速度稳定区和静子壁面速度下降区,稳定区的速度为转子线速度的一半左右。转子和静子壁面处的涡量大于中心处涡量,并且沿径向高涡量区和低涡量区有明显界限。
(3)间隙内的摩擦损失随着压力增加呈线性增加。比较发现,当10
<
<6×10
时,模型2的预测结果与数值计算结果更接近,最大相对偏差为1.44%。当
>6×10
时,模型4与数值计算结果更接近,两者之间的最大相对偏差为6.15%,并且相对偏差随着流体压力的增大基本不变。
:
[1] 曹润, 李志刚, 邓清华, 等. 超临界二氧化碳离心压气机设计和气动性能研究 [J]. 西安交通大学学报, 2020, 54(4): 44-52.
CAO Run, LI Zhigang, DENG Qinghua, et al. Design and aerodynamic performance investigation of supercritical carbon dioxide centrifugal compressor [J]. Journal of Xi’an Jiaotong University, 2020, 54(4): 44-52.
[2] CAO Run, LI Zhigang, DENG Qinghua, et al. Design and aerodynamic performance investigations of centrifugal compressor for 150 kW class supercritical carbon dioxide simple brayton cycle [C]∥Proceedings of the ASME Turbo Expo 2020: Turbomachinery Technical Conference and Exposition. New York, NY, USA: ASME, 2020: V011T31A019.
[3] 姜世杰, 李志刚, 李军. 凹槽状小翼对涡轮动叶叶顶气动和传热性能的影响 [J]. 西安交通大学学报, 2019, 53(9): 7-14.
JIANG Shijie, LI Zhigang, LI Jun. Effects of squealer winglet on the aerodynamic and heat transfer performances of turbine rotor blade tip [J]. Journal of Xi’an Jiaotong University, 2019, 53(9): 7-14.
[4] 张凤阁, 蒋晓东, 李应光, 等. 新型磁障转子无刷双馈电机热计算 [J]. 中国电机工程学报, 2018, 38(9): 2745-2752.
ZHANG Fengge, JIANG Xiaodong, LI Yingguang, et al. Thermal calculation on brushless doubly-fed machines with a magnetic barrier rotor [J]. Proceedings of the CSEE, 2018, 38(9): 2745-2752.
[5] CONBOY T, WRIGHT S, PASCH J, et al. Performance characteristics of an operating supercritical CO
Brayton cycle [J]. Journal of Engineering for Gas Turbines and Power, 2012, 134(11): 111703.
[6] NACHOUANE A B, ABDELLI A, FRIEDRICH G, et al. Estimation of windage losses inside very narrow air gaps of high speed electrical machines without an internal ventilation using CFD methods [C]∥Proceedings of the 2016 XXII International Conference on Electrical Machines (ICEM). Piscataway, NJ, USA: IEEE, 2016: 2704-2710.
[7] VRANCIK J E. Prediction of windage power loss in alternators [EB/OL]. (1968-10-01)[2021-09-24]. https:∥ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov /19680027690.pdf.
[8] WENDT F. Turbulente strömungen zwischen zwei rotierenden konaxialen zylindern [J]. Ingenieur-Archiv, 1933, 4(6): 577-595.
[9] YAMADA Y. Torque resistance of a flow between rotating co-axial cylinders having axial flow [J]. Bulletin of JSME, 1962, 5(20): 634-642.
[10]BILGEN E, BOULOS R. Functional dependence of torque coefficient of coaxial cylinders on gap width and Reynolds numbers [J]. Journal of Fluids Engineering, 1973, 95(1): 122-126.
[11]SAARI J. Thermal analysis of high-speed induction machines [D]. Helsinki: Helsinki University of Technology, 1998.
[12]刘难生, 董宇红, 陆夕云, 等. 旋转同心圆筒间Couette-Taylor流动的数值模拟 [J]. 中国科学技术大学学报, 2002, 32(1): 91-97.
LIU Nansheng, DONG Yuhong, LU Xiyun, et al. Numerical simulation of the Couette-Taylor flow between two concentric rotating cylinders [J]. Journal of University of Science and Technology of China, 2002, 32(1): 91-97.
[13]杜珩, 阙夏, 刘难生. 不同半径比Taylor-Couette湍流的直接数值模拟研究 [J]. 中国科学技术大学学报, 2014, 44(9): 761-768.
DU Heng, QUE Xia, LIU Nansheng. Influence of radius ratio on Taylor-Couette turbulent flow using direct numerical simulation [J]. Journal of University of Science and Technology of China, 2014, 44(9): 761-768.
[14]LIU Mingda, SIXEL W, DING Hao, et al. Investigation of rotor structure influence on the windage loss and efficiency of FSPM machine [C]∥Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ECCE). Piscataway, NJ, USA: IEEE, 2018: 6499-6505.
[15]ANDERSON K R, LIN Jun, WONG A. Experimental and numerical study of windage losses in the narrow gap region of a high-speed electric motor [J]. Fluids, 2018, 3(1): 22.
[16]XU Jinliang, SUN Enhui, LI Mingjia, et al. Key issues and solution strategies for supercritical carbon dioxide coal fired power plant [J]. Energy, 2018, 157: 227-246.
[17]CONBOY T, PASCH J, FLEMING D. Control of a supercritical CO
recompression Brayton cycle demonstration loop [C]∥Proceedings of the ASME Turbo Expo 2013: Turbine Technical Conference and Exposition. New York, NY, USA: ASME, 2013: V008T34A007.
[18]ZHAO Hang, DENG Qinghua, ZHENG Kuankuan, et al. Numerical investigation on the flow characteristics of a supercritical CO
centrifugal compressor [C]∥Proceedings of the ASME Turbo Expo 2014: Turbine Technical Conference and Exposition. New York, NY, USA: ASME, 2014: V03BT36A013.
[19]LI Zhigang, LI Zhuocong, LI Jun, et al. Leakage and rotordynamic characteristics for three types of annular gas seals operating in supercritical CO
turbomachinery [J]. Journal of Engineering for Gas Turbines and Power, 2021, 143(10): 101002.
[20]YUAN Tao, LI Zhigang, LI Jun, et al. Design and analysis of cooling structure for dry gas seal chamber of supercritical carbon dioxide turbine shaft end [C]∥Proceedings of the ASME Turbo Expo 2021: Turbomachinery Technical Conference and Exposition. New York, NY, USA: ASME, 2021: V010T30A012.
[21]蒋宇. 超临界二氧化碳动力循环原理样机综合设计及系统热力性能优化研究 [D]. 西安: 西安交通大学, 2019.
[22]梁腾和, 黄宏立, 马乐, 等. 涡轮机械转子在CO
工质中风摩损耗的数值分析 [J]. 厦门大学学报(自然科学版), 2020, 59(4): 522-547.
LIANG Tenghe, HUANG Hongli, MA Le, et al. Numerical analysis of windage loss of turbomachinery rotor in CO
[J]. Journal of Xiamen University(Natural Science), 2020, 59(4): 522-547.
[23]ADEBAYO D S, RONA A. Numerical investigation of the three-dimensional pressure distribution in Taylor Couette flow [J]. Journal of Fluids Engineering, 2017, 139(11): 111201.
[24]BEN NACHOUANE A, ABDELLI A, FRIEDRICH G, et al. Numerical approach for thermal analysis of heat transfer into a very narrow air gap of a totally en-closed permanent magnet integrated starter generator [C]∥Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE). Piscataway, NJ, USA: IEEE, 2015: 1749-1756.
[25]COLES D. Transition in circular Couette flow [J]. Journal of Fluid Mechanics, 1965, 21(3): 385-425.
[26]GOLLUB J P, SWINNEY H L. Onset of turbulence in a rotating fluid [J]. Physical Review Letters, 1975, 35(14): 927-930.
