新型冠状病毒肺炎传播动力学模型构建与分析
2022-05-21于振华黄山阁杨波高红霞卢思
新型冠状病毒肺炎(coronavirus disease 2019,COVID-19,简称新冠肺炎)在全球肆虐已长达一年半之久,原本已经得到稳定控制的疫情近期又呈现出二次暴发的趋势。截至2021年5月1日,新冠肺炎已经在印度、日本等多个国家二次暴发,新冠病毒的变异使疫情规模加速扩大,给社会经济发展造成巨大影响。近年来,传染病动力学研究进展迅速,大量数学模型被用于分析各种各样的传染病问题,以探索传染病一般传染规律
。因此,为了对新冠肺炎的传播规律进行研究,并对新冠肺炎传播趋势进行预测,可通过建立新冠肺炎传播数学模型,研究其传播趋势,分析不同群体的变化规律,探索抑制新冠肺炎传播的有效防控手段,这对于疫情治理具有重要的理论和实际意义。
在现有的传染病模型中,最具代表性的有SIR(susceptible-infected-recovered)、SIRS(sus-ceptible-infected-recovered-susceptible)、SEIR(susceptible-exposed-infected-recovered)等经典的传染病模型
。目前,针对新冠肺炎特点,也建立了相应的模型对其进行研究。在经典的SIR模型基础上,Jia等
运用动态扩展的SIR模型对意大利疫情进行分析和预测,估计出疫情持续时间。Cooper等
利用SIR模型对美国德克萨斯州的不同社区进行了研究,得出了采取适当的防控策略可以将社区疫情进行控制的结论。喻孜等
提出了时变参数的SIR模型,针对武汉的新冠肺炎进行了相关分析。Kudryashov等
采用SIR模型对较小疫情群体进行仿真分析,预测结果较好。Alenezi等
将SIR模型应用于科威特新冠肺炎疫情的分析预测,预测出该国的感染峰值。Lymperopoulos
将神经网络与SIR模型结合对新冠肺炎疫情进行评估,其预测效果良好。Lux
从社会动力学角度出发,运用SIR模型对欧洲各国新冠疫情进行分析,提出了控制疫情蔓延的方法。SIR模型的局限性在于其适用性受到限制,只能在疫情暴发阶段且有足够数据时可用,而且此模型对群体状态划分考虑不够充分,没有划分潜伏者、无症状感染者等,也没有考虑个人防护、政府管控等因素,对现实情况考虑不够完善。
病虫害是影响花卉观赏性及生长情况的重要因素。对于不同的花卉,病虫害的具体类型存在差异,因此应做好防控工作,采用综合措施提升对花卉的管理水平。花卉病虫害防治应以预防为主,通过加强花卉的田间管理,控制农药的使用,有效避免农药残留。花卉病虫害防治方法具体包括农业防治、生物防治、物理防治及药物防治等。
我继续说:“大风吹。”孩子们都想被叫到,声音一个比一个高:“吹哪里?”“吹赵鹤翔。你上课勤于思考,回答问题特别积极,调动了课堂气氛,老师很喜欢你。”他吐了吐舌头,说:“谢谢老师。”
除了经典的SIR模型,国内外许多学者也提出了其他改进模型。孙皓宸等
将校园新冠肺炎数据与传统SEIR模型结合,验证了数字追踪防控策略的有效性。王国强等
基于不同年龄层接触模式建立了SEIHR(susceptible-exposed-infected-hospitalized-recovered)新冠肺炎传播模型,对不同年龄段群体新冠肺炎的传播趋势进行了分析,研究发现居家模式对疫情的控制具有良好的有效性。李盈科等
介绍了关于新冠肺炎的潜伏期、代间隔和基本再生数等几个重要流行病学参数的研究进展和相应的估计方法。范如国等
运用SEIR模型对武汉的新冠肺炎拐点进行了预测分析。Carcione等
通过改变SEIR模型中感染期的上下限对意大利的疫情进行分析,并对疫情峰值进行了预测。Ivorra等
以SEIR模型为基础提出了SEIHRD(susceptible-exposed-infected-hospitalized-recovered-dead)模型,研究了不同检测病例比例对中国新冠肺炎疫情规模的影响。Jahanshahi等
通过分阶的SIRD模型对23个国家新冠肺炎时间序列数据进行分析,提出了运用多重分式方法可以更有效地预测新冠肺炎感染总人数的结论。Kuniya
基于SEIR模型利用带泊松噪声的最小二乘方法,估计了日本疫情的基本再生数,并对当下流行病学提出了相关建议。周武略等
把SEIR模型改进为SEAIC(susceptible-exposed-asymptomatic-infected-CT)模型,对武汉疫情初期的防控提出相关建议。Yarsky
设计了一种新的遗传算法,通过该算法可将美国各个州的数据与现有的SEIR模型匹配,取得了较好的拟合效果。López等
通过使用随机修正SEIR模型来探索不同的隔离情景,研究了潜伏期间感染的传播趋势,论证了保持社交距离和个人非药物干预可能消除封锁的必要性。Raslan
提出一种扩展SEIR模型分析和预测埃及新冠肺炎,预测结果与实际报告数据误差较小,并在此基础上讨论了隔离期时长对疫情的影响。杨波等
考虑实际防控措施,提出了一个新的新冠肺炎传播动力学模型,该模型能较准确地模拟新冠肺炎的传播动态,并利用武汉及湖北其他地区数据对该模型进行验证。以上模型均为SEIR模型的拓展,此类模型对群体状态划分考虑更加全面,反映出更多群体状态的变化趋势,但是部分模型过于复杂,难以对其动力学行为进行分析和验证,无法在动力学的基础上更好地了解疫情的动态传播过程。此外,以上大多数模型对参数采取了固定的取值策略,没有考虑到参数的动态变化,因此对疫情整体发展状况的预测不够准确。
通过对新冠肺炎传播的规律和特点研究,本文将疫情中的人群划分为易感者S(susceptible)、低危群体L(low-risk)、潜伏者E(exposed)、感染者I(infected)和治愈者R(recovered),建立了新的SLEIR模型,并对模型的平衡点、稳定性及分岔进行了分析,揭示新冠肺炎的传播机理。疫情发展过程是一个动态过程,其发展趋势会受各种因素影响,进而导致模型参数发生变化,本文在实际数据的基础上使用最小二乘参数估计方法,对模型参数进行分段估计,从而提高疫情预测精度。最后利用该模型对印度疫情的传播趋势进行模拟仿真、预测与分析,取得了较好的效果,说明SLEIR模型可以对新冠肺炎的传播趋势起到一定的预警和预测作用。
1 SLEIR模型假设和建立
1.1 模型假设
考虑到新冠肺炎疫情的特点,本文建立了一个新的SLEIR模型。此模型将人群分为易感染者(S)、低危群体(L)、潜伏者(E)、感染者(I)、治愈者(R)共5个群体。其中,易感染者(S)指不采取任何保护措施且未染病的群体,该群体在与感染者密切接触时,会有一定概率被病毒感染;低危群体(L)指采取保护措施且未染病的群体(例如佩戴口罩),该群体在与感染者密切接触时,感染病毒的概率较易感者大大降低;潜伏者(E)指被病毒感染但仍处于染病潜伏期的群体;感染者(I)指已经被病毒感染且疾病暴发的群体;治愈者(R)指感染病毒后被治愈的群体。现对新模型提出以下假设。
(1)在模型中,
(
)、
(
)、
(
)、
(
)、
(
)分别表示
时刻S、L、I、E、R状态群体占总人口的比例,假设模型总人口始终保持为一个常数,对任意时刻
均有
(
)+
(
)+
(
)+
(
)+
(
)=1。
(2)易感染者和低危群体均可能被病毒感染。
在第一个感恩节餐桌上出现的酸甜蔓越莓酱或蔓越莓果冻今天仍然供应。蔓越莓是一种小而酸的浆果。它生长在马萨诸塞州和新英格兰地区其他州的沼泽地或泥泞地区。印第安人用水果来治疗感染。他们用果汁染地毯和毯子。他们教殖民者如何用甜味剂和水煮浆果来制作酱汁。印第安人称之为“ibimi”,意思是“苦浆果”。当殖民者看到它时,他们称之为“鹤浆果”,因为浆果的花把茎折弯了,很像长颈的鹤。这些浆果仍然生长在新英格兰地区。
(3)考虑人口的出生、死亡、流动等种群动力因素,在动力系统中模拟出人口的流动,即易感群体和低危群体的补充及各群体的人口流出
,假设模型人口进入率为
,人口退出率为
。为简化计算,假设模型总人口恒定,那么人口进入率和退出率相同,人口进入和退出率
=
=
。
(4)一个病人(潜伏者或感染者)一旦与易感染者和低危群体发生接触行为则可能会造成传染。假设单位时间
内,一个病人感染易感染者和低危群体的数量与接触到的该群体数量成正比,感染率分别为
和
,故在单位时间
内易感染者和低危群体被感染数分别为
(
)(
(
)+
(
))和
(
)(
(
)+
(
))。
(5)根据新型冠状病毒的特点,易感染者被感染后存在潜伏周期,假设在本模型中,感染者只能通过潜伏者转化。假设单位时间
内,潜伏者转化为感染者的数量与此环境内潜伏者
(
)成正比,潜伏暴发率为
,从而在单位时间
内感染者的增量为
(
)。
(6)受医疗卫生水平影响,假设单位时间
内,感染者被治愈的数量与感染者
(
)成正比,治愈率为
,从而单位时间内治愈者的增量为
(
)。为进一步简化模型,暂且不考虑治愈者复阳情况。
基于上述假设,SLEIR模型的状态转移如图1所示。

1.2 模型的建立
根据上面的状态转移过程,利用非线性动力学理论对其进行动力学建模,构建出新冠肺炎传播SLEIR模型,表达式如下

(1)
式中:
为易感染者占新加入人口的比例;
和
分别为易感群体S和低危群体L的感染率。
对于模型(1),由假设可知
(
)+
(
)+
(
)+
(
)+
(
)=1,且前4个方程均不包含
(
),故实际上只需讨论前4个方程,将
(
)=1-(
(
)+
(
)+
(
)+
(
))代入模型(1),可约简为如下微分动力系统

(2)
由现实情况可知,S、L、E、I、R这5个群体皆为正数,系统(2)满足初始条件
(
)≥0,
(
)≥0,
(
)≥0,
(
)≥0,其状态空间
={(
(
),
(
),
(
),
(
)):
(
)≥0,
(
)≥0,
(
)≥0,
(
)≥0}。由于
为正不变集,因此只需考虑初始条件处于
内的解,其在
内具有存在性及唯一性。
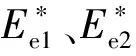
=(
,1-
,0,0)
(3)

(4)

(5)
其中
问卷设计以城市天际线的视觉美观程度为依据。审美心理中形成的总体体验被称作审美愉快,这种感受是美感的认识活动和美感的情感活动综合作用的结果[13]。因此,问卷将愉悦感作为评价依据,引导受访者根据愉悦感强弱对各段天际线的美学特征进行相应评价。评价根据李克特量表形式将愉悦程度由强到弱划分为5级:非常愉悦、比较愉悦、愉悦、比较不愉悦、非常不愉悦,分别赋值为5、4、3、2、1。

(6)
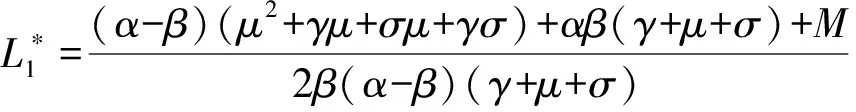
(7)


(8)


(9)

(10)

(11)
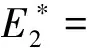

(12)


(13)
=(((
-
)(
+
+
+
)+
(
+
+
))
-
噢噢,好了!小六子真的没有死!他不仅没有死,这个黑不溜秋的小家伙好着呢。没事就好!小六子没有事就好!我看到小六子他人后,在心里这样默默地祈祷了一气,心里的一块石头才放下来。

(14)
根据系统(2)和再生矩阵法
,有
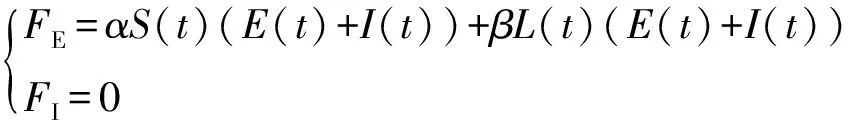
(15)
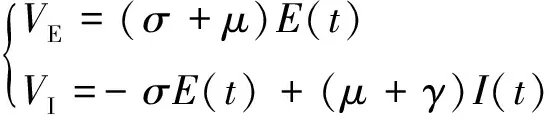
(16)
将平衡点
的取值代入
和
矩阵,则有
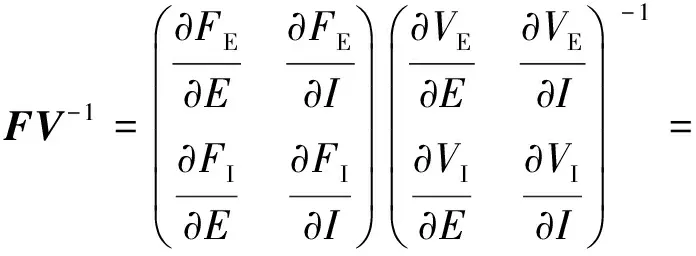


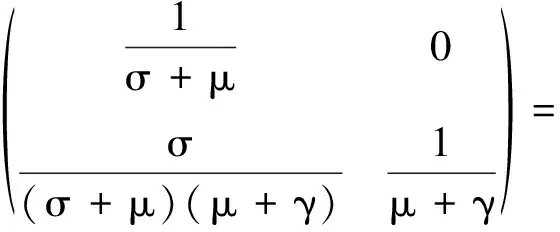

(17)
通过计算,矩阵(17)的谱半径为
1个月后,对照组和观察组低血压发生情况分别为:10例38.46%、2例7.69%,x2=26.802,p=0.000;高血压发生情况分别为:18例69.23%、5例19.23%,x2=50.674,p=0.000;低血糖发生情况分别为:7例26.92%、1例3.85%,x2=20.441,p=0.000;心脑血管疾病发生情况分别为:13例50.00%、3例11.54%,x2=34.719,p=0.000;感染发生情况分别为:7例26.92%、2例7.69%,x2=12.920,p=0.000;组间比较结果P<0.05。由于部分患者同时伴有多种并发症,因此数据统计有重复情况发生。
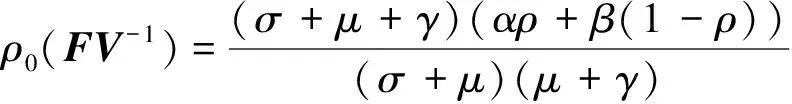
(18)
故系统(2)的基本再生数
为
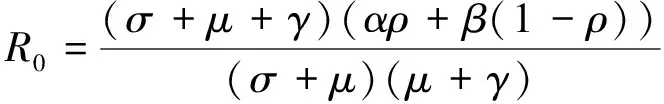
(19)
基本再生数
是一个非常重要的概念,它表示在发病初期,当所有人均为易感者时,一个感染者在其平均感染周期内所能感染的人数。
=1是区分疾病流行与否的阈值。
2 SLEIR模型动力学行为分析
2.1 平衡点及其稳定性分析
当且仅当
<1时,系统(2)在无病平衡点
渐进稳定。
系统(2)在无病平衡点
处的雅可比(Jacobi)矩阵为

(20)
通过计算可知
的特征根为
=-
(21)

(22)
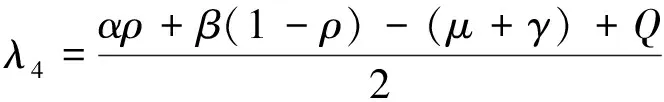
(23)
其中
=(
(
-
)
+2(
+
+2
)(
+
(1-
))+
(2
+
(1-2
)))
12
(24)
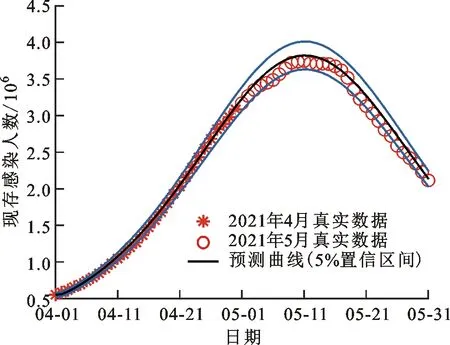
通过对印度2021年4月数据进行拟合,将拟合出的参数估计代入系统(2),将生成的预测曲线与5月份疫情真实数据进行比较,预测相对误差为2.805%,预测曲线如图8所示。

令
=0.2,
=0.1,
=0.15,
=0.4,
=0.15,
=0.15,则
=0.7<1。根据定理1,系统(2)的无病平衡点渐进稳定。当政府通过采取一系列措施对疫情进行管控,降低感染率
;或者通过加大医疗行业投入使治愈率
提高,使
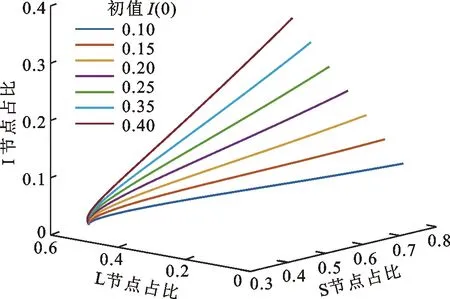
<1时,疫情将会在短期内结束。通过仿真,此时系统(2)不同状态群体的演化曲线如图2所示。图3为当I状态群体比例分别为0.10、0.15、0.20、0.25、0.30、0.35、0.40,
<1时,仿真后叠加形成的S-L-I平面相轨图。
They kept on walking until they found an 2)oasis, where they decided to take a bath. The one who had been slapped got stuck in the 3)mire and started 4)drowning,but the friend saved him.

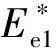


(25)

式(25)的特征方程为
+
+
+
+
=0
(26)
其中
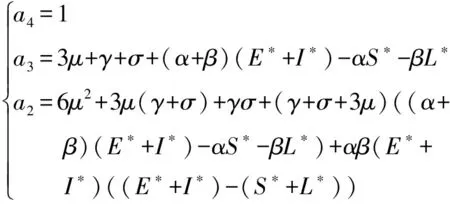
(27a)
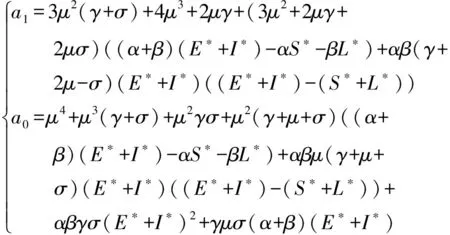
(27b)
根据Routh-Hurwitz判定准则,可得
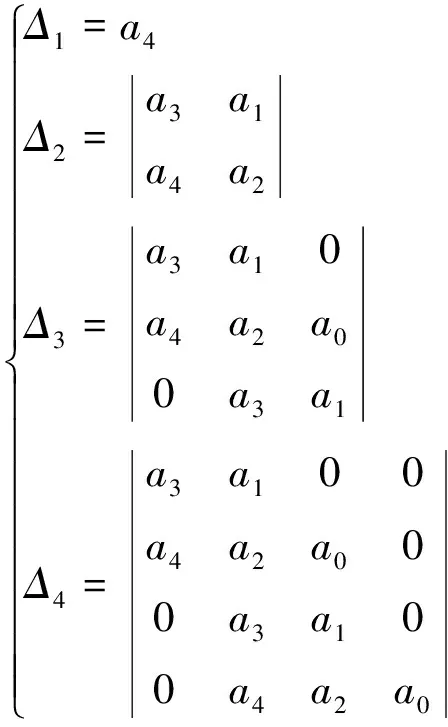
(28)

令
=0.4,
=0.2,
=0.15,
=0.4,
=0.15,
=0.15,则
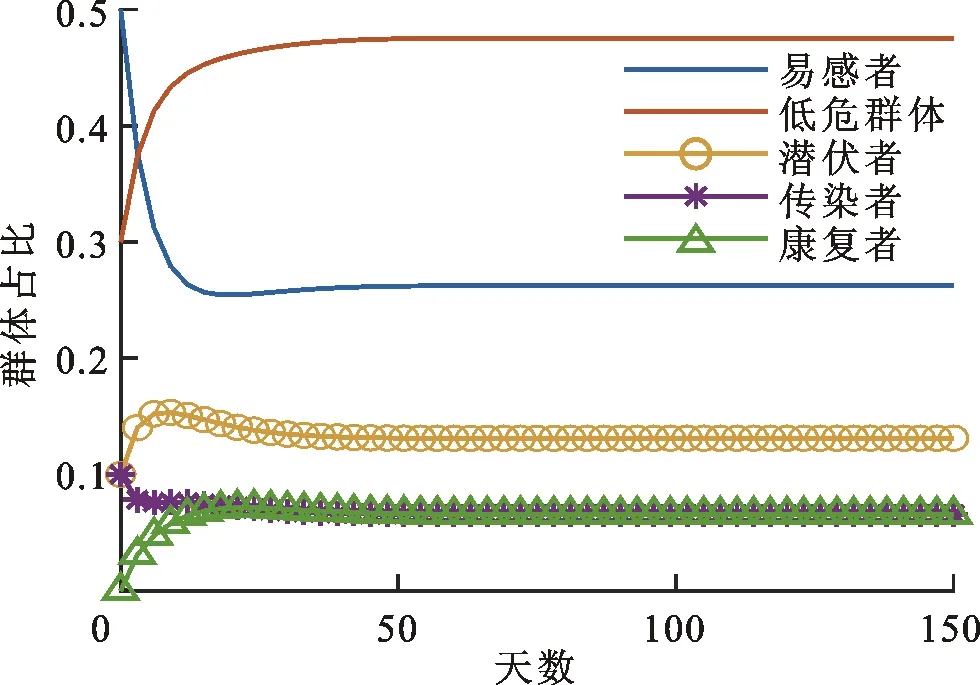
=1.4>1。根据定理2,系统(2)的地方病平衡点渐进稳定。当政府对于新冠肺炎缺乏管控经验时,感染率
处于较高水平;或者由于对医疗行业投入较少,使治愈率
处于低值,导致
>1,疫情将迅速暴发并持续发展,如印度疫情二次暴发前期,若对疫情不加控制,最终将会达到一个平衡状态,会有恒定比例的感染者存在。通过仿真,此时系统(2)的各状态群体演化曲线如图4所示。图5为当I状态群体比例分别为0.10、0.15、0.20、0.25、0.30、0.35、0.40,
>1时,仿真后叠加形成的S-L-I平面相轨图。

2.2 分岔分析
当
=1时,系统(2)在无病平衡点
处发生跨临界分岔。
当
=1时,系统(2)在无病平衡点
处雅可比矩阵的特征方程为
+
+
+
=0
(29)
显然此特征方程的一个特征根为0,故
为非双曲平衡点。

基本再生数
是影响新冠肺炎持续传播的一个重要因素。若政府对疫情不够重视,对疫情防控缺乏经验,会使感染率
升高,则
>1,疫情将会一直持续下去;若政府对疫情的管控采取主动积极的措施,使感染率
降低,则有
<1,疫情将最终消亡。
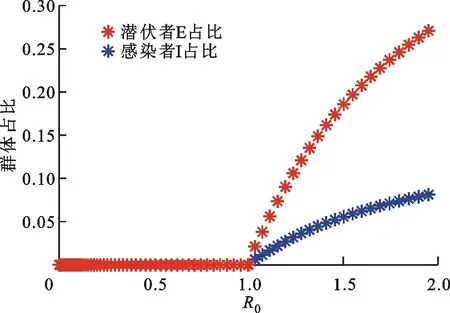
的取值与处于平衡点时感染者群体I和潜伏者E的占比关系如图6所示。从图6中可以看出,在
=1邻域内,系统(2)发生跨临界分岔。
4
(
-
)(
+
+
)(
+
+
+
))
12
要推进医院财务会计内部控制工作,就必须确保预算管理工作有序进行,医院管理者要从加强各部门之间的互相监督着手,从整体的预算管理抓起,确保医院资源得以充分应用。只有对资金应用做好准确预算,才能确保后续资金使用的有效性,推动医院财务管理更正规和科学地发展。因此医院财务管理信息化建设必须大力推动实施,积极引进信息化财务管理体系,保证预算工作的准确性,便于后续财务预算管理更顺利实行,从而达到控制医院资金收支平衡,充分发挥会计核算财务管理实际效果的目标。
3 基于SLEIR模型的疫情预测与分析
3.1 参数估计
平均相对误差定义如下式
当增压舱A舱(驾驶舱)出现破孔时,A舱空气外泄,导致的A舱压力急剧下降,其他增压舱室空气通过各舱室间的补气通道直接或者间接向A舱补气。由于各舱室容积和舱室间流通面积不同,导致各舱室的压力下降相较于A舱有一定的滞后,最终造成各舱室的泄压曲线和各舱室之间的压差变化曲线不同。在计算模型中需要明确各舱室的体积以及各舱室之间的流通面积和流通关系。
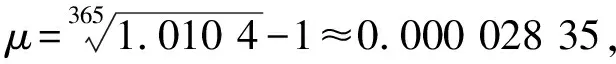
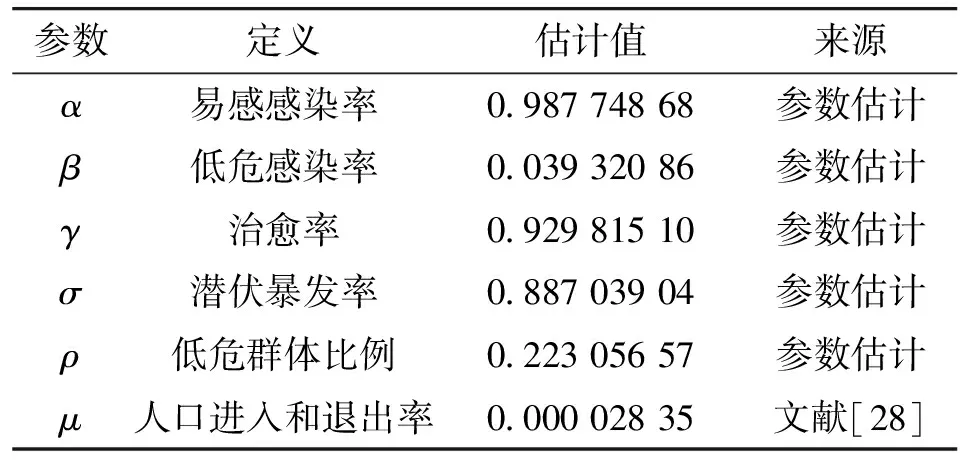
通过对霍普金斯大学所统计的2021年3月1日至2021年5月30日印度全国新冠肺炎数据,将其分为两个阶段,分别采用最小二乘法对模型进行参数估计,其第1阶段与第2阶段参数估计结果如表1和表2所示。

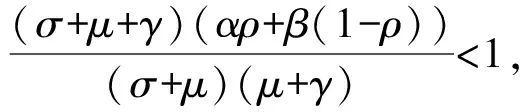
为了揭示新冠肺炎传播规律,预测疫情发展趋势。通过考虑疫情传播实际情况,以真实数据为依据,对SLEIR模型中的参数进行估计。

(30)
3.2 疫情预测
3.2.1 印度2021年3~4月疫情预测分析
通过对印度2021年3月疫情数据的拟合,将拟合出的参数估计代入系统(2),并将所得到的预测曲线与印度2021年4月的真实数据进行比较,预测相对误差为4.107%,预测曲线如图7所示。

通过对印度3月份的参数进行估计后,根据所估计的数值计算出其基本再生数
=0.958 1<1,可见印度疫情并不会一直延续下去,但是由于基本再生数接近于1,其疫情控制速度将极其缓慢。
设A=(a1,a2,…,an)为多属性决策问题中n个方案构成的方案集C=(c1,c2,…,cm)是由m个属性组成的属性集,ω=(ω1,ω2,…,ωm)为属性的权重向量,且满足:决策者在每一个属性下对各个方案的评价值用智立方数表示。
3.2.2 印度2021年4~5月疫情预测分析
通过对霍普金斯大学所统计的印度全国2021年4月1日至2021年5月30日新冠肺炎数据,采用最小二乘法对模型进行参数估计如表2所示。
由图2及表4可得出,咪唑啉、季铵盐、酰胺盐3种缓蚀剂的自腐蚀电位均正移,膦酸盐缓蚀剂的自腐蚀电位负移,加入缓蚀剂后,体系的自腐蚀电流密度均降低,自腐蚀电流密度越小,腐蚀反应越慢,从而缓蚀剂的缓蚀率越高,缓蚀率分别为83.65%、86.01%、87.64%和94.13%。其中,膦酸盐缓蚀剂的缓蚀率高达90%以上。
通过计算易得
<0,当
=
通过对表2中的参数估计进行观察后,发现其中易感感染率
≈0.987 7,接近于1,但是基本再生数
=0.583 19,处于一个低的估计值。因此,正如当下传染病领域的相关专家对印度数据的质疑
,本文通过对印度真实疫情数据拟合后得出的参数估计进行分析,同样也认为印度疫情的真实情况可能比官方数据公布的更加严重,其官方公布的疫情数据存在一定的异常情况,在3.3节SEIR模型的比较中也体现出了这种数据的异常。
3.2.3 印度9~10月及未来疫情预测分析
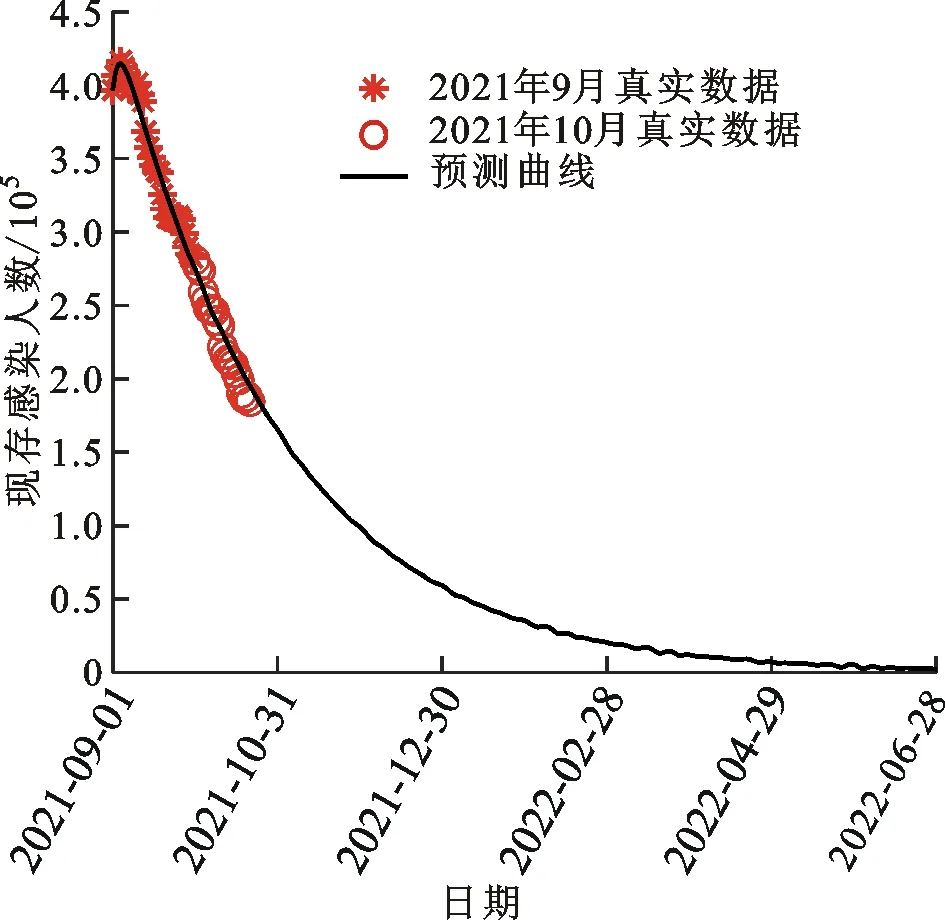
对印度3~5月份新冠肺炎疫情的预测充分说明了SLEIR模型的有效性。为了对印度长期疫情做出预测,首先将9月份疫情数据代入模型中进行参数估计,参数估计结果如表3所示,预测相对误差为3.266%,预测曲线如图9所示。


通过图9可以看出,SLEIR模型对于印度当前疫情具有较好的预测效果。假设在政府管控措施不变的情况下,通过SLEIR模型对印度之后的疫情发展做出预测,结果如图10所示。从图10结果可以看出,若病毒感染率不发生变化,印度的现存感染人数预计将在2021年12月份降至10万人以下,整个疫情预计将在2022年6月底结束。
产品结构上,茅台酱香系列酒从三年前的20几个品牌200多个品种,调整到现在的10个品牌60个品种,实施品牌、品种双瘦身,效益在上升。
3.3 不同模型仿真比较
本节通过SLEIR模型与传统SEIR模型的对比,比较两个模型对于疫情预测的差异。
对于SEIR模型
,有如下微分动力系统
综上所述,配网自动化能够保证电力系统可以正常运行,提高供电的可靠性。随着社会的进步与科技水平的不断提高,配网自动化技术未来的发展会更加光明。文章结合配电网自动化技术概念及运用优势,就配电网运行中的问题,提出了一此可行性的解决措施,为进一步推动配网自动化技术的应用提供了有效的参考依据,增强了配电网供电可靠性。
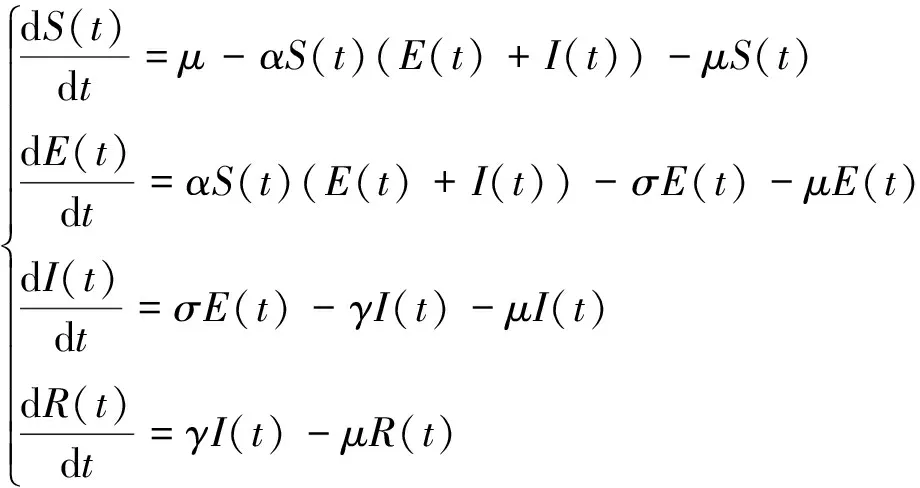
(31)
基于2021年3月印度新冠肺炎数据对SEIR模型重新使用最小二乘参数估计,其参数估计值如表4所示(SLEIR参数估计值为表1估计值),预测相对误差为15.796%(SLEIR模型为4.107%),预测曲线如图11所示。

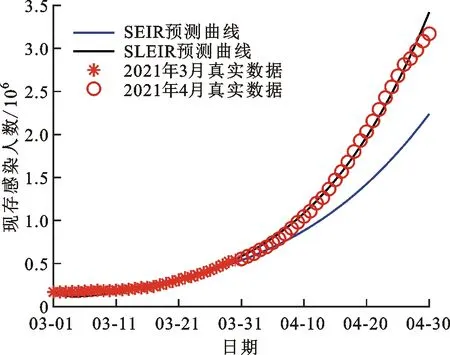
由图11和表4可以看出,根据SEIR模型进行疫情预测后,SLEIR模型的预测误差优于SEIR模型。因此,采取SLEIR模型对疫情的预测更符合实际。从仿真中也可以看出,根据实际数据对模型参数进行估计,对于提高模型预测精度是有必要的。
按照上述方法对SEIR模型进行第2阶段的拟合预测,其相关参数估计值如表5所示,预测相对误差为204.175%,预测曲线如图12所示。
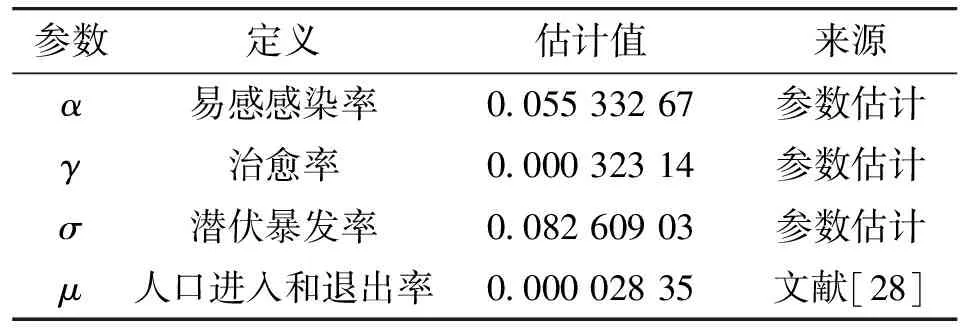
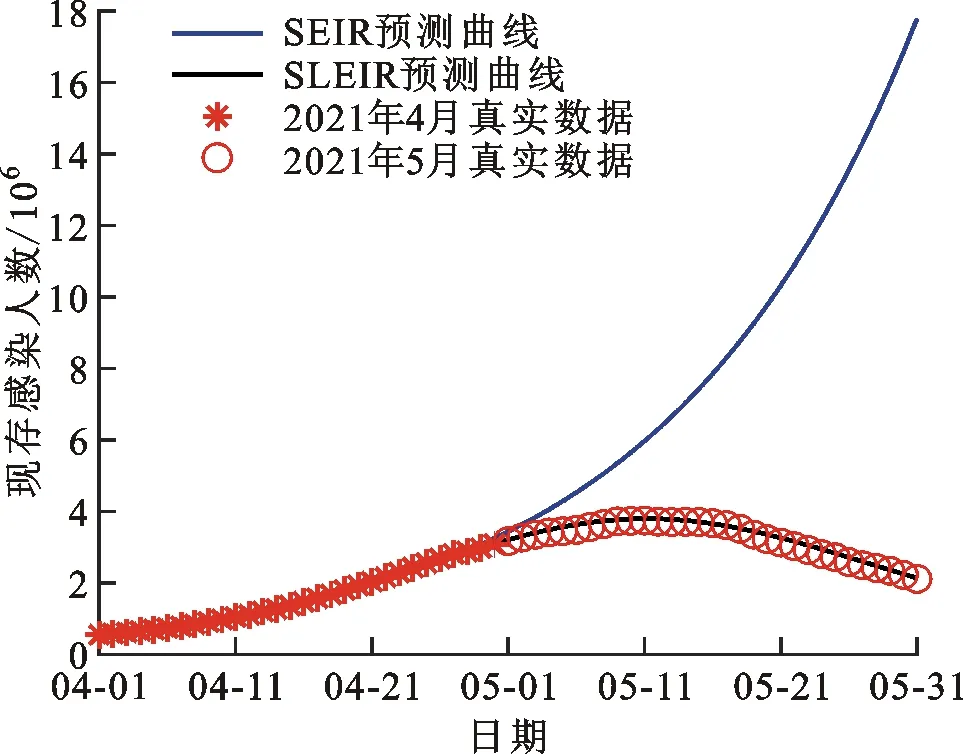
由表5可以看出,SEIR模型在第2阶段相对误差超过100%,已经无法达到预测效果,通过图12对SEIR模型的拟合预测曲线进行观察,SEIR模型预测效果差,无法反映出真实情况。此外,对表9中SEIR的参数估计值进行观察,其中易感感染率
≈0.055 3,治愈率
≈0.000 3,显然这种参数的估计值出现异常。
将SLEIR模型与SEIR模型进行比较,可以发现SLEIR模型对于第1、第2阶段的拟合预测均有良好的拟合结果,相较于SEIR模型可以适应更复杂的疫情状况。此外,通过对SLEIR和SEIR模型第2阶段参数估计值的异常情况进行观察,对印度2次疫情暴发中现存感染人数迅速转折下降的情况存有质疑,其数据不符合传染病发展规律,正如现在国内外专家对印度疫情状态的讨论和质疑
。
4 结 论
为了研究新冠肺炎传播的规律和机理,建立了一种新的新冠肺炎传播SLEIR模型,并从动力学角度对模型的平衡点、稳定性及分岔等性质进行分析,揭示了新冠肺炎的传播机制。采用最小二乘法对模型参数进行分段估计,模型预测精度更高,在对印度真实情况的拟合方面,该模型对印度疫情的两个阶段拟合度较高。将该模型用于印度新冠肺炎传播趋势预测中,其预测结果与真实数据也比较吻合,通过SLEIR模型对印度疫情最新的数据进行预测,取得了较好的效果,并对印度疫情的未来发展做出估计。最后,将SLEIR模型与传统动力学模型进行比较,新的SLEIR模型在多个阶段的预测误差均优于传统SEIR模型,进一步验证了模型的有效性以及对复杂真实情况的适应性,表明该模型能够对政府控制疫情发展做出一定程度上的参考。
:
[1] PINTO C M A, CARVALHO A R M. A latency fractional order model for HIV dynamics [J]. Journal of Computational and Applied Mathematics, 2017, 312: 240-256.
[2] CANDIDO D S, CLARO I M, DE JESUS J G, et al. Evolution and epidemic spread of SARS-CoV-2 in Brazil [J]. Science, 2020, 369(6508): 1255-1260.
[3] ROOSA K, LEE Y, LUO Ruiyan, et al. Short-term forecasts of the COVID-19 epidemic in Guangdong and Zhejiang, China: February 13-23, 2020 [J]. Journal of Clinical Medicine, 2020, 9(2): 596.
[4] ARAZI R, FEIGEL A. Discontinuous transitions of social distancing in the SIR model [J]. Physica: A Statistical Mechanics and Its Applications, 2021, 566: 125632.
[5] KIOUACH D, SABBAR Y. Global dynamics analysis of a stochastic SIRS epidemic model with vertical transmission and different periods of immunity [J]. International Journal of Dynamical Systems and Differential Equations, 2020, 10(5): 468-491.
[6] ALRABAIAH H, ARFAN M, SHAH K, et al. A comparative study of spreading of novel corona virus disease by using fractional order modified SEIR model [J]. Alexandria Engineering Journal, 2021, 60(1): 573-585.
[7] JIA Wangping, HAN Ke, SONG Yang, et al. Extended SIR prediction of the epidemics trend of COVID-19 in Italy and compared with Hunan, China [J]. Frontiers in Medicine, 2020, 7: 169.
[8] COOPER L, MONDAL A, ANTONOPOULOS C G. A SIR model assumption for the spread of COVID-19 in different communities [J]. Chaos, Solitons & Fractals, 2020, 139: 110057.
[9] 喻孜, 张贵清, 刘庆珍, 等. 基于时变参数-SIR模型的COVID-19疫情评估和预测 [J]. 电子科技大学学报, 2020, 49(3): 357-361.
YU Zi, ZHANG Guiqing, LIU Qingzhen, et al. The outbreak assessment and prediction of COVID-19 based on time-varying SIR model [J]. Journal of University of Electronic Science and Technology of China, 2020, 49(3): 357-361.
[10]KUDRYASHOV N A, CHMYKHOV M A, VIGDOROWITSCH M. Analytical features of the SIR model and their applications to COVID-19 [J]. Applied Mathematical Modelling, 2021, 90: 466-473.
[11]ALENEZI M N, AL-ANZI F S, ALABDULRAZZAQ H. Building a sensible SIR estimation model for COVID-19 outspread in Kuwait [J]. Alexandria Engineering Journal, 2021, 60(3): 3161-3175.
[12]LYMPEROPOULOS I N. #stayhome to contain Covid-19: Neuro-SIR: Neurodynamical epidemic modeling of infection patterns in social networks [J]. Expert Systems with Applications, 2021, 165: 113970.
[13]LUX T. The social dynamics of COVID-19 [J]. Physica: A Statistical Mechanics and Its Applications, 2021, 567: 125710.
[14]孙皓宸, 刘肖凡, 许小可, 等. 基于连续感染模型的新冠肺炎校园传播与防控策略分析 [J]. 物理学报, 2020, 69(24): 68-77.
SUN Haochen, LIU Xiaofan, XU Xiaoke, et al. Analysis of COVID-19 spreading and prevention strategy in schools based on continuous infection model [J]. Acta Physica Sinica, 2020, 69(24): 68-77.
[15]王国强, 张烁, 杨俊元, 等. 耦合不同年龄层接触模式的新冠肺炎传播模型 [J]. 物理学报, 2021, 70(1): 204-214.
WANG Guoqiang, ZHANG Shuo, YANG Junyuan, et al. Study of coupling the age-structured contact patterns to the COVID-19 pandemic transmission [J]. Acta Physica Sinica, 2021, 70(1): 204-214.
[16]李盈科, 赵时, 楼一均, 等. 新型冠状病毒肺炎的流行病学参数与模型 [J]. 物理学报, 2020, 69(9): 15-24.
LI Yingke, ZHAO Shi, LOU Yijun, et al. Epidemiological parameters and models of coronavirus disease 2019 [J]. Acta Physica Sinica, 2020, 69(9): 15-24.
[17]范如国, 王奕博, 罗明, 等. 基于SEIR的新冠肺炎传播模型及拐点预测分析 [J]. 电子科技大学学报, 2020, 49(3): 369-374.
FAN Ruguo, WANG Yibo, LUO Ming, et al. SEIR-based COVID-19 transmission model and inflection point prediction analysis [J]. Journal of University of Electronic Science and Technology of China, 2020, 49(3): 369-374.
[18]CARCIONE J M, SANTOS J E, BAGAINI C, et al. A simulation of a COVID-19 epidemic based on a deterministic SEIR model [J]. Frontiers in Public Health, 2020, 8: 230.
[20]JAHANSHAHI H, MUNOZ-PACHECO J M, BEKIROS S, et al. A fractional-order SIRD model with time-dependent memory indexes for encompassing the multi-fractional characteristics of the COVID-19 [J]. Chaos, Solitons & Fractals, 2021, 143: 110632.
[21]KUNIYA T. Prediction of the epidemic peak of coronavirus disease in Japan, 2020 [J]. Journal of Clinical Medicine, 2020, 9(3): 789.
[22]周武略, 白迪, 赵继军. 武汉市发生的新冠病毒肺炎建模研究分析 [J]. 复杂系统与复杂性科学, 2020, 17(4): 58-65.
ZHOU Wulüe, BAI Di, ZHAO Jijun. Modeling and Analysis of COVID-19 in Wuhan [J]. Complex Systems and Complexity Science, 2020, 17(4): 58-65.
[23]YARSKY P. Using a genetic algorithm to fit parameters of a COVID-19 SEIR model for US states [J]. Mathematics and Computers in Simulation, 2021, 185: 687-695.
[25]RASLAN W E. Fractional mathematical modeling for epidemic prediction of COVID-19 in Egypt [J]. Ain Shams Engineering Journal, 2021, 12(3): 3057-3062.
[26]杨波, 于振华, 蔡远利. 新型冠状病毒肺炎传播与控制数学建模研究[J]. 西安交通大学学报, 2021, 55(11): 162-172.
YANG Bo, YU Zhenhua, CAI Yuanli. Mathematical modeling for spread and control of COVID-19[J]. Journal of Xi’an Jiaotong University, 2021, 55(11): 162-172.
[27]马知恩, 周义仓, 王稳地, 等. 传染病动力学的数学建模与研究 [M]. 北京: 科学出版社, 2004: 116-126.
[28]观研报告网. 2010-2018年印度人口总数和年度增长率数据统计表[EB/OL]. (2020-04-09)[2021-08-27].http:∥data.chinabaogao.com/hgshj/2020/0494X005 2020.html.
[29]Center for Global Development. Bloomberg: COVID may have claimed as many as 5 million lives in India[EB/OL].(2021-07-21)[2021-08-27]. https:∥www. cgdev.org/article/bloomberg-covid-may-have-cla imed-many-5-million-lives-india.
[30]Center for Global Development. BBC Newshour: India COVID deaths may be ten times the official rate[EB/OL]. (2021-07-20)[2021-08-27]. https:∥www. cgdev.org/article/bbc-newshour-india-covid-deaths-may-be-ten-times-official-rate.
