基于改进蚁群算法的参数寻优在过热汽温控制中的应用

李思莹

随着机组容量越来越大，运行环境愈加复杂，PID控制逐渐无法满足过热汽温的控制品质要求。近年来，基于深度学习的控制策略开始逐渐运用到工程中，其中蚁群算法就被广泛运用到工业控制领域中。

受到蚁群觅食的启发，学者M.Dorigo提出蚁群算法[1]。蚁群算法具有较强的正反馈性，但是收敛慢、收敛精度较差。针对蚁群算法的缺陷，众多学者做出了改进。柳长安等结合狼群算法改进信息素更新规则，用粒子群算法对重要参数寻优，提高蚁群收敛与搜索速度[2]。张立毅等将模拟退火机制引入蚁群算法并加入了混沌扰动，提高了收敛速度，同时增强了搜索能力[3]。陈迎欣采用混合的信息素更新策略、着眼全局改进启发因子，并引入搜索热区提高蚁群搜索效率[4]。李擎等结合粒子群-蚁群混合算法，改进的信息素更新方式,信息素全局同步更新的同时增强精英蚂蚁信息素，加快了收敛速度[5]。袁亚博等在信息素浓度初始化加入方向引导因子,改进局部和全局信息素更新规则[6]。但是，以上算法没有在连续域的前提下对信息素进行自适应改进，所以寻优时范围有限，并且易陷入局部最优。

数学家保罗·莱维提出“莱维飞行”概念，这是一种在连续域中采用随机步长来描绘莱维分布的方法[7]。蔡敏等基于“莱维飞行”的思想，优化映射算法避免局部最优[8]。赵洪等利用莱维飞行搜索能力，引入高斯核函数来调节莱维飞行的步长，提高搜索效率[9]。本文提出了一种改进的蚁群算法，将莱维飞行的思想运用到信息素蒸发系数的寻优中，较好地克服了“早熟”现象，提高了收敛速度。最后将这种改进的蚁群算法用于过热汽温控制的模型辨识和控制器参数优化中，改善了过热汽温的控制品质。

1 蚁群算法

蚁群算法模拟蚂蚁的行为特性，算法的提出主要用于解决旅行商问题(Traveling Salesman Problem, TSP)。TSP假设一位商人要按照顺序依次拜访S座城市，相邻两个城市之间有10条道路可供选择，但是每个城市只拜访一次，且不能回访，最终使所取得的路径的路程为所有路径中最短。

1.1 编码规则

首先定义一个城市之间的有向多重图，如图1。其城市节点集合为{C1,C2,…,CS}。每个城市只与相邻城市相连，且每两相邻城市之间存在10条路径可供选择。蚂蚁从起始点出发直到终点，期间不重复经历任何城市。

图1 有向多重图

若优化问题解的维数为N，那么城市个数S是N的整数倍，即

S=L×N

(1)

式(1)中L为整数，表示编码长度。蚂蚁从起点开始，依次走过每个城市直到终点，得到优化的一个X={xi|i=1,2,…,N}。蚂蚁每经过L个城市，即得到一个变量xi。设第k只蚂蚁所形成的轨迹为{pk1,pk2,…,pks}，则该蚂蚁路径对应的解为：

(2)

xi=(xiH-xiL)ei+xiL

(3)

式(2)中，pkj表示蚂蚁k从第j个城市作为起点走过的路径，pkj∈[0,10]，ei为xi归一化后的数值，xiH和xiL为xi的上下限。

1.2 优化过程

首先，在特定值范围内的随机数初始化各路径上的信息素。然后令所有蚂蚁开始遍历各个城市。蚂蚁按照概率公式(4)选择下一路径。

(4)

(5)

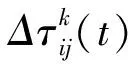
(6)

其中，Q为信息素强度。为加强最优路径对蚂蚁行为的影响，就需强化其信息素，即

(7)

(8)

直到达到最大遍历次数Nc为止。最终输出最优路径对应的解。

蚁群算法解决TSP的步骤如下：m只蚂蚁同时从某城市出发，根据式(4)选择下一城市。一次遍历后，由式(5)和式(7)更新各条路径上的信息素，对最佳路径反复执行上述过程，直到终止条件成立。

2 改进的蚁群算法

2.1 蚁群算法的局限性

在传统蚁群算法中，信息素蒸发系数ρ决定了算法的搜索能力和收敛速度[10]。ρ值过小，会使重复选择路径的概率加大，使算法的随机性能和搜索能力降低；ρ值过大，增多了无用搜索，降低了收敛速度[11]。

2.2 莱维飞行

莱维飞行由数学家保罗·莱维提出，对随机和伪随机现象的模拟有广泛的应用[12]。但缺陷是最优解的搜索范围存在局限性。本文将莱维飞行的思想运用到信息素蒸发系数ρ的寻优中，可以实现一部分解在当前最优值附近搜索，另一部分解离相对较远的空间搜索，防止局部最优。

2.3 基于莱维飞行思想的蚁群算法

由于莱维飞行轨迹繁复，实现起来很困难，所以使用Mantegna算法模拟飞行产生的随机步长和方向[13]，位置更新如下：

(9)

(10)

其中：β∈[1,2]，Γ为标准Gamma函数。v服从正态分布。

借鉴莱维飞行模式得到信息素残留系数ρ的位置更新，即为

(11)

3 基于改进蚁群算法的过热汽温控制系统参数寻优

3.1 过热汽温控制系统

3.1.1 系统结构

喷水减温是最为普遍的控制过热汽温的手段。它的结构简单，调温范围大，调节灵敏。大型锅炉中，过热器一般采用分段控制。过热汽温的结构简图如图2所示。

图2 过热汽温串级控制系统结构简图

3.1.2 动态特性

在蒸汽扰动下，温度的响应变化具有自平衡性，而且惯性和延迟时间较小。蒸汽流量变化对过热器汽温的影响如图3所示。

图3 蒸汽流量变化对过热器汽温的影响

烟气的温度、流速以及流量等变化，都会导致汽温变化，且呈正相关特性。在烟气量扰动下，汽温响应变化快，并且延迟时间短。烟气流量变化对过热器汽温的影响如图4所示。

图4 烟气流量变化对过热器汽温的影响

减温水流量扰动是导致汽温变化的主要原因，汽温随减温水流量减少而上升。由于过热器管道长，并且是一个多容对象，因此汽温具有较大的延迟。减温水量变化对过热器汽温的影响如图5所示。

图5 减温水量变化对过热器汽温的影响

3.1.3 串级控制策略

控制对象的输入信号为减温水流量，输出信号为出口温度θ1，辅助调节信号为减温器出口温度θ2，用于改善系统的动态特性。当减温水阀门动作时，导前汽温θ2变化快于过热器出口温度θ1。串级控制系统的原理图如图6所示。

图6 串级控制系统原理方框图

3.2 基于改进蚁群算法的参数寻优

模型辨识本质上是根据热工系统动态特性，得到模型函数的结构，最终得到模型参数。因此，系统辨识的本质即参数的优化。

假定某热工过程的稳态的数学模型为：

(12)

式(12)中，被控对象的输入和输出为u，y；θ=[kTnτ]为参数实际值；θ*=[k*T*n*τ*]为参数估计值。辨识原理图如图7所示。

图7 辨识原理图

y(t)为系统实际输出，y(k)为y(t)的采样值，e(k)为预估模型与实际输出采样值之差。模型辨识要寻找最优估计参数θ*，使得下式目标函数值最小。

(13)

导致控制系统性能变差的原因有很多，例如控制器缺少维护或整定效果不好、设备故障、干扰模型的变化、系统的控制结构设计不恰当等。通过性能评价及时发现控制系统性能下降，针对性能差的控制系统，整定参数将控制器的状态保持在最优，对工业生产安全有重要意义。

完成过热汽温模型辨识后，再次采用改进蚁群算法对串级控制器参数进行优化，达到最终系统预期的效果，最后应用于实际工业过程中。

3.3 工程仿真

本文数据来自某电厂600MW机组，以二级减温控制系统为例来介绍试验建模方法。

3.3.1 主汽温模型辨识

在530MW工况下，将B侧二级喷水减温器调节阀开度从38.33%调节至48.33%，减温水流量从12.09t/h增长到27.75t/h，减温器出口温度迅速变化，而主汽温的变化呈现出大延迟、大惯性的特点。保存被调量汽温变化和调节量减温水的变化数据，数据采样周期为1s，如图8所示。

图8 530MW工况B侧二级减温水扰动试验曲线

串级控制系统需辨识两个模型，一个是减温水流量到减温器出口汽温的数学模型；另一个是减温器出口汽温到主汽温数学模型。二级减温器出口温度(导前汽温)的变化曲线表现出有惯性、有自平衡的特性，因此可以选择有自平衡的多阶对象作为模型结构。主汽温的变化曲线表现出有惯性、有延时、有自平衡特性，因此选择有自平衡对象中的具有纯迟延的高阶惯性对象作为模型结构。

530MW负荷工况下，对调节量扰动下汽温响应曲线进行辨识，辨识结果如下。

导前区模型为：

(14)

惰性区模型为：

(15)

将原始数据的减温水调节量输入作用在辨识得到的模型中，图9给出了模型输出与实测数据的曲线对比。由图可以看出，导前汽温的实际输出曲线呈现出不规则的波形，是由于现场工况复杂，不能严格控制其他影响量不变，蒸汽量和烟气量的变化都将引起过热汽温的变化。导前汽温辨识得到的模型输出曲线能较好的与实际曲线拟合，主汽温的曲线拟合精度高，因此，辨识结果可信。

图9 模型输出与实测数据的对比

3.3.2 控制器参数整定

依照历史数据辨识出的过热汽温对象模型，控制框图设计如图10所示。分别采用常规的经验法和智能优化算法整定控制器参数。

图10 530MW工况下过热汽温串级控制系统

(1)目标函数的选取

误差积分型目标函数比单项品质指标更能综合考虑快速性、平稳性和准确性之间的平衡关系。时间乘绝对误差积分准则(ITAE)考虑到了偏差和调节时间，在ITAE的基础上，引入调节量惩罚项。通过调整权重的大小，防止控制器输出剧烈振荡。如下所示：

(16)

c1、c2分别为误差和控制量在目标函数中的权重。

(2)控制器参数优化

选择一组初始参数，作为优化参数的中心点，在中心点上下浮动30%范围作为优化参数的上下限。将目标函数中的权重值c1、c2分别定为0.25和0.75。

采用改进蚁群算法对内回路控制器的比例系数和外回路控制器的比例系数、积分时间、微分时间进行参数寻优，优化结果为kc1=1.30，Ti1=110.59，Td1=19.35,kc2=1.63。常规蚁群算法得到的参数为kc1=1.87，Ti1=118.51，Td1=36.11,kc2=1.31。两组不同参数控制的响应曲线如图11所示。

图11 基于蚁群算法整定的主汽温响应曲线

算法目标函数值收敛曲线如图12所示。常规蚁群算法经过13次迭代后收敛，陷入局部最优；改进蚁群算法仅迭代5次就找到了全局最优解，收敛速率快，验证了改进算法的有效性。

图12 目标函数值收敛曲线

对比三种参数寻优方法下的阶跃响应曲线，如图13所示。可以看出，采用常规经验法整定结果得到响应曲线上升速度较慢，调节时间约为430s。采用蚁群算法对控制器参数寻优得到的响应曲线上升速度较快，调节时间约为315s。利用改进蚁群算法优化的系统，大约在284s便达到稳定状态。改进蚁群算法寻优得到的控制器参数控制结果最好。

图13 三种不同方法整定的主汽温响应曲线

4 结论

针对传统蚁群算法在寻优时范围有限，并且易陷入局部最优的缺点，提出了一种改进的蚁群算法，将莱维飞行的思想运用到信息素蒸发系数的寻优中。通过这种方法可以扩大最优解的搜索范围，避免陷入局部最优。为了验证该方法的有效性，本文采用国内某600MW火电机组的历史运行数据，先后完成了过热汽温控制系统的模型辨识和主副回路控制器的参数优化。通过与改进前蚁群算法进行仿真对比，实验结果表明，本文提出的改进蚁群算法在寻优的过程中，迭代次数减少约61.5%，收敛速度提高约9.84%，可以较好克服“早熟”现象，避免了陷入到局部最优，验证了本文提出的基于改进蚁群算法进行参数优化的有效性。