无碳避障小车路径规划与凸轮设计分析*

吕晨茜，李宏鹏，常 浩，马炬宾，卢志鹏，沈国茂，王淑珍，王小义

(兰州交通大学 机电工程学院，甘肃 兰州 730070)

0 引 言

无碳小车是全国大学生工程训练综合能力竞赛的设计主题之一，对提高学生的工程实践能力与培养学生的创新意识和团队精神都具有重要意义。近年来，一些学者对无碳小车的设计进行了研究，极大地提高了无碳小车的设计水平和运行能力。例如Dong等人[1]设计了无碳小车的双8字形轨道和盘形凸轮，同时设计了微调机构，通过对微调机构参数的调整，尽可能使无碳小车运行时的误差大大减少；Han等人[2]，首先将双8字形轨道抽象成数学模型并完成了轨道的设计，其次对影响轨迹的参数进行了研究，设计了小车的整体结构，最后将设计好的小车进行仿真实验，并通过无碳小车的运行表现对参数进行修改；同时笔者也参考学习了文献[3]～[7]关于无碳小车路径规划设计方面的内容。重点针对无碳小车避障路径规划和凸轮设计，采用三角函数的基本理论，对“8”字型避障路径及对应的凸轮设计进行了研究，并用同样的方法生成了“S”型臂章路径。所提方法高效实用，可应用于任意避障路径的规划和凸轮设计，对无碳小车的路径规划和设计具有重要的指导意义。

1 操作现场描述

无碳小车运行场地为5 200 mm×2 200 mm的矩形平面区域，如图1。

图1 竞赛场地

图1中粗实线分别为边界挡板和中间隔板，中间隔板长度为1 000 mm且厚度不超过12 mm，并且两个隔板之间有1 000 mm的活动间隙；10个障碍物是直径为20 mm、高200 mm的圆棒(图1中黑色圆点)；其中，8个中间障碍物之间的横向距离为1 000 mm，与隔板中心线的垂直距离为550 mm，左右两侧的障碍物在半径为550 mm的圆上。左下角和右上角的阴影区域为出发区域。由于原理相同，文中仅给出S型详细的路径规划和凸轮设计方案。S型路径如图2所示，小车整体简图与转向原理分别如图3、4。

图2 “S”形运行轨迹

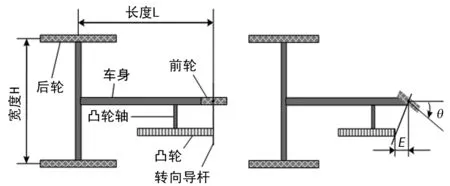
图3 小车车体俯视图 图4 小车前轮转向示意

2 避障路径规划

(1)

(2)

式中：X、A和T分别为函数的变量、幅值和周期。

由于曲率半径是曲率的倒数，故有：

(3)

式中：ρ为曲率半径，K为曲率。

为便于计算，规定图2路径中所有圆弧部分的曲率半径相等且ρ=350 mm。

首先，规划桩2和桩4之间的路径。如图5，以2号桩为原点，连接2、3、4号桩建立轴X1，并建立相应的轴Y1。

(4)

曲线1对应的余弦函数为：

(5)

当A1<ρ时，点2′处的曲率半径相对应的圆心O2在轴X1的下方，O2-2′两点间的距离为ρ；当A1>ρ(虚线小圆)时，点2′处的曲率半径所对应的圆心O2′在轴X1的上方，O2′-2′两点间的距离为A1-ρ。通过计算得出：A1<ρ，所以O2-2两点间的距离为ρ-A1=350-289=61 mm。

图5 曲线1的设计图

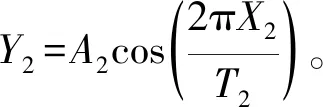
图6 曲线2～4的设计图

从图5、6的几何关系可知：

H=550-(O2-2)=550-61=489 mm

因为图6中虚线在点10′处的曲率半径必须等于ρ，所以可根据式(4)得出T2所对应的幅值A2：

(6)

此时，完成桩10、1、2之间的初步路径规划(图6虚线所示)，其所对应函数如下：

(7)

为了使实际路径曲线2以桩10为圆心和ρ为半径的圆相切，需将初步路径沿轴Y2移动至点10″，其移动距离为ρ-A2=350-191=159 mm。至此，完成曲线2的路径设计。

(8)

显然，曲线3、4的曲率半径ρ相等，且曲线3、4的弧长可由式(10)、(11)确定：

(9)

(10)

(11)

则曲线5对应的余弦函数为：

(12)

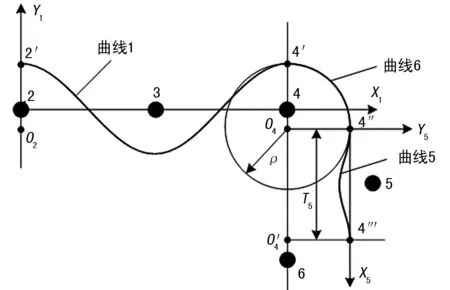
图7 曲线5、6设计图

从图2可看出，整个路径关于中心线对称。因此，桩10、9、8之间的曲线和曲线2，桩8、7、6之间的曲线和曲线1及右下角的1/4圆弧和右上角的1/4圆弧都关于中心线对称。因为两个对称曲线的函数表达式完全一致，所以此处不再计算。通过以上分析，可计算出S形轨迹中的各分段函数。在此基础上，用MATLAB绘出图2中的路径，如图8。

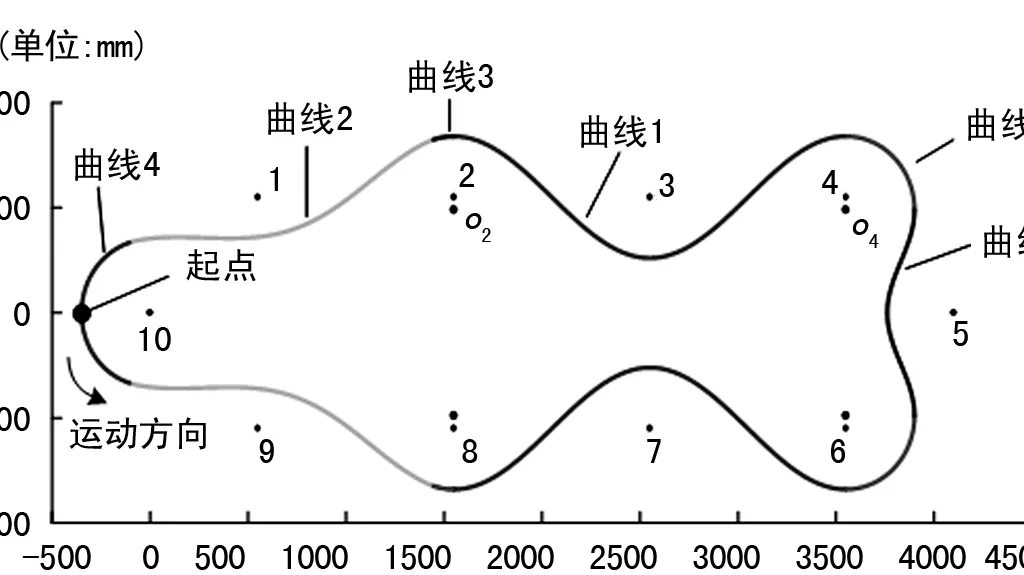
图8 “S”形路径图

图8中的环形路径是由多段圆弧和多个完整三角函数组成。同时，桩4、5、6之间的曲线5也可由1/4的三角函数和直线组成，

同样利用上述方法可获得8字形路径，如图9。

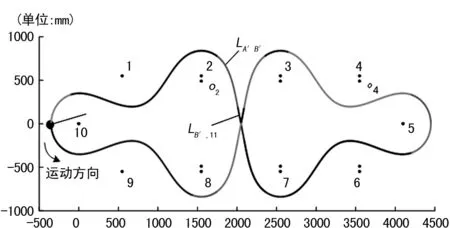
图9 “8”字形路径图

3 凸轮设计

3.1 计算前轮转角

根据几何关系，前轮旋转角度θ等于圆心角λ。侧轮的轨迹为运行路径时，可得出前轮转角θ为：

传统授课模式下，教学主要采用课堂讲授方式，教学过程是单向的，授课过程是教师的独角戏，通常是教师制订课程标准、教学计划及教学方案，然后开展教学。教师为了完成任务而教学，完全忽略掉了学生在教学过程中的主观能动性和主体地位，学生变成了知识的容器，完全处于被动接受的地位。这样做的结果通常是教师在课堂上侃侃而谈，学生在课堂上昏昏欲睡，学生缺乏学习的积极性，教学效果很差。

(13)

式中：ρ为曲率半径；L为小车长度；H为小车宽度。

小车转向时，小车前、后轮的曲率圆为同心圆。只要计算出小车路径的曲率半径，就可得到相应的前轮转角θ，如图10所示。

图10 前轮转角θ图

假设小车的长度L和宽度H分别为150 mm和110 mm，从图8的出发点开始，沿着路径行驶方向可计算出相应路径点的前轮转动角度。当小车前轮左转时，角度为负；前轮右转时，角度为正。图8中路径对应的前轮转动角度如图11。图中DO是转向导杆的延长线，O为同心圆的圆心。

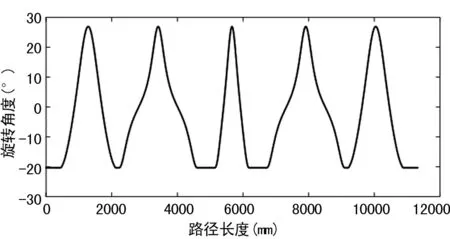
图11 “S”形路径前轮转角图

3.2 计算凸轮轮廓

根据几何关系，缩短量E和伸长量e′与旋转角度θ之间的关系如下：

(14)

(15)

小车向右转和向左转的凸轮实际半径分别为：

Rs=r-EE′

(16)

凸轮的旋转角度ξ为：

(17)

式中：Sn为沿路径行驶方向上路径每一点到起始点的路径长度；S是规划路径的总长度。

由于路径是显函数组合而成，所以路径长度可通过积分方法来计算，其中S形路径S1=811 325 mm、8字形路径S2=13 708 mm。

通过公式(18)、(19)计算出凸轮轮廓的每一点坐标，利用MATLAB绘制出凸轮轮廓。

(18)

(19)

通过查阅资料可知：偏心凸轮能够减小转向导杆与凸轮轮廓接触时的压力角。文中所述的偏心凸轮是指转向导杆的中心轴线位置O′相对于凸轮中心轴线O的升高或降低，其偏心距为e。图14中左右两图分别对应图12、13中的两种情况。

图12、13中，r是凸轮基圆半径，p是转向导杆的横截面半径，d是凸轮厚度的1/2，t是小车车体对称中心面与凸轮厚度对称面的距离。根据几何关系，可得凸轮实际半径Rs和Rs′为：

图12 凸轮半径缩短时前轮向右转示意图

图13 凸轮半径伸长时前轮向左转示意图

图14 偏心凸轮的设计图

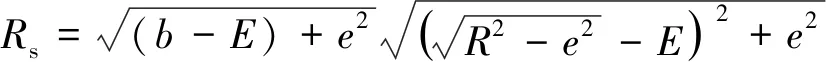
(20)

(21)

将式(27)、(29)、(30)带入式(22)中，同样可绘制出凸轮轮廓。

通过以上分析，并根据表1所列的车体参数可对S形轨迹和8字形轨迹进行凸轮设计，分别为图15、16。其结果表明，偏心凸轮的最大半径比非偏心凸轮的最大半径小，偏心凸轮的最小半径比非偏心凸轮的最小半径大，这使得偏心凸轮轮廓比非偏心凸轮轮廓更光滑。因此，偏心凸轮更有利于小车的运行，其转向导杆的自锁概率也更小。

表1 车体参数

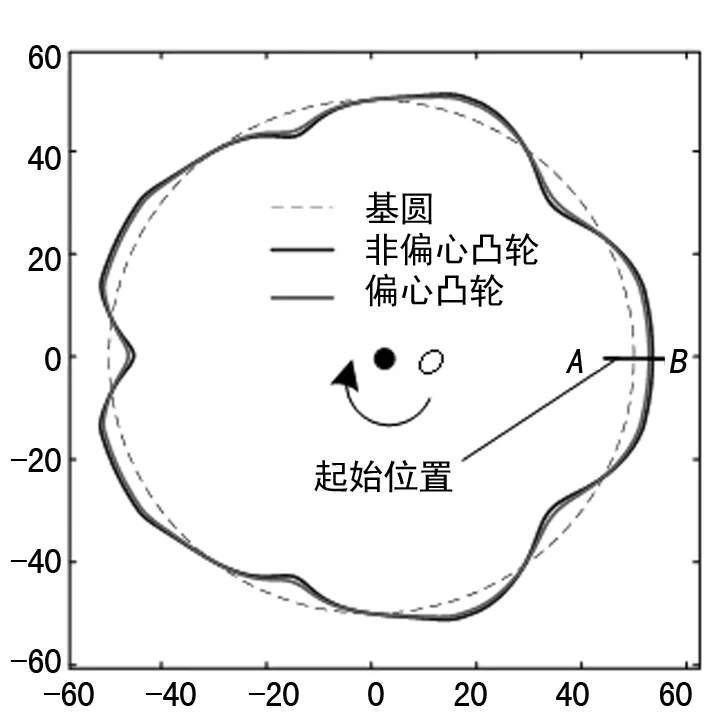
图15 “S”形凸轮

图16 “8”字形凸轮

3.3 凸轮仿真验证

在确定无碳小车各参数的情况下，可用仿真来验证凸轮的合理性、稳定性。尽量在仿真环节中检查出存在的问题，以最大限度避免后期反复实验造成的时间和成本的浪费。此次通过Motion分析对8字形非偏心凸轮进行运动轨迹仿真验证。

取主动轮直径D=170 mm，可得8字形轨迹对应的传动比i为：

(22)

结合表1中的车体结构参数，对8字形非偏心凸轮进行仿真，其效果图如图17、18。

可以看出：运行多圈时轨迹会产生较小偏移，但从整体上看，全程运行轨迹重复性良好，无撞桩情况发生，满足赛题要求。仿真结果表明，此方法设计的凸轮是合理有效的，其稳定性良好。这与后期制作出的小车实物实际测试的结果基本吻合，满足精度要求和设计目标，符合使用条件。

图17 单圈轨迹仿真效果图

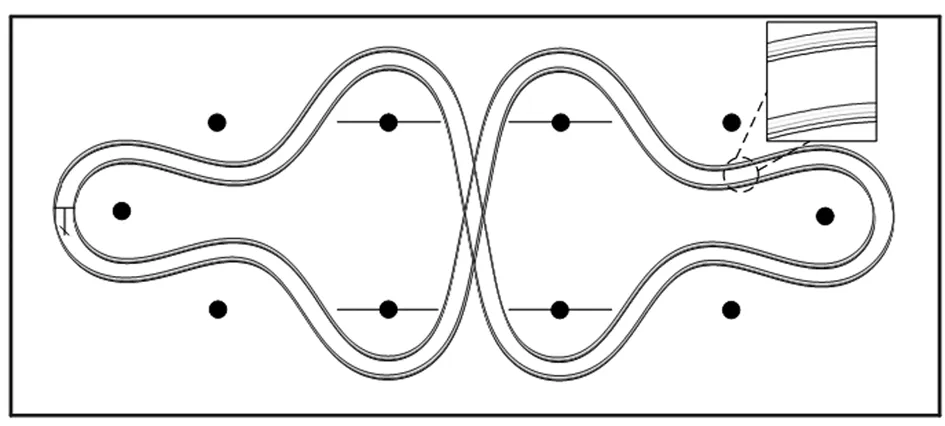
图18 多圈轨迹仿真效果图

4 结 语

研究了基于三角函数的避障路径规划方法和凸轮轮廓的设计。该方法充分利用了余弦函数曲率连续光滑的优点和特点，其曲率半径可从无穷大变为某一特定值，然后结合圆弧和直线设计出小车路径。文中所提小车路径设计方法具有普遍性，通过调整余弦函数的周期及振幅就可得到任何曲率半径连续光滑的运行路径；通过路径函数和小车车体的几何关系，可计算出前轮转角；根据转向机构的几何关系可计算出凸轮的轮廓；根据转向导杆和凸轮的位置关系，提出了偏心凸轮的设计方法；通过Motion分析验证了该方法的有效性、合理性，符合实际设计理论，具有较强的适应性。结果表明，偏心凸轮轮廓比非偏心凸轮轮廓更光滑，在一定程度上降低了自锁的可能性。