最优化方法课程研究性教学之初探——拉格朗日乘子法*

孙 敏，葛 静

(枣庄学院数学与统计学院，山东 枣庄 277160)

引言

最优化理论与方法是运筹学的一个重要分支，其包含了线性规划、非线性规划、组合优化、动态规划以及最优控制等最优化模型.学者们对这些最优化分支进行了深入的研究，针对每个分支，相应的最优化理论与求解算法都已经相当完善[1].在求解约束优化问题的方法中，拉格朗日乘子法因为其良好的数值表现以及在实际生活中的广泛应用而获得了学者们更多的关注.

拉格朗日乘子法是《最优化理论与方法》的重点，也是一个教学难点.本文中，拟对拉格朗日乘子法的教学进行探讨，对这块内容采用层次化教学模式：动机→目标→算法→扩展→应用，层层递进，由浅入深，以一种立体的形式将这个知识点慢慢展示给学生，进而达到分散难点的目的.

1 拉格朗日乘子法的设计动机

考虑等式约束优化问题

minf(x)
s.t.h(x)=0

(1)

其中f(x):Rn→R,h(x):Rn→Rl.外罚函数法通过引入罚因子，对不满足约束的点实施惩罚，将约束优化问题(1)转化为一系列的无约束优化问题.为了让这些无约束优化问题的最优解向(1)的可行域靠近，需要让罚因子趋于正无穷，而这会给求解无约束优化问题带来困难.下面通过一个例子来说明当罚因子趋于无穷大时，无约束优化问题会发生什么变化.

例1 考虑约束最优化问题

minf(x)=(x1-1)2+2(x2-1)2

s.t.x1+x2=1

解 引入增广目标函数Pσ(x)=(x1-1)2+2(x2-1)2+σ(x1+x2-1)2,

取[0,0]T作为初始迭代点，罚因子取为σk=k，利用最速下降法求解第k个子问题(k=0,1,2,…)

minPσk(x)=(x1-1)2+2(x2-1)2+σk(x1+x2-1)2.

计算过程的信息见表1.

表1 利用最速下降法求解子问题的信息

由表1可以得到，随着子问题目标函数条件数的增大，子问题的迭代次数变得越来越大，到了第100 000次迭代，子问题没有求解成功.可以从几何上解释如下：目标函数的条件数越大，其等高线越来越密集，因此使用梯度类算法求解将会变得非常困难[2].于是为了提高算法的计算效果，需要设计一种罚因子不需要趋于无穷的罚函数法，而拉格朗日乘子法就是这样一类算法.

2 拉格朗日乘子法的设计思路

问题(1)的拉格朗日函数是L(x,λ)=f(x)-λTh(x)，KKT条件是

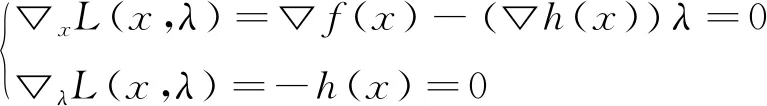
(2)

其中λ∈Rm为拉格朗日乘子.下面将系统(2)视为求解目标.问题(1)的外罚法的子问题是

其最优性条件是

▽Pσk(x)=▽f(x)+σk(▽h(x))h(x)=0

(3)

这说明每次求解外罚法的子问题时，实际得到了方程(3).对比系统(2)，方程(3)中缺少了拉格朗日乘子项，因此补充这一项得

▽f(x)-(▽h(x))λ+σk(▽h(x))h(x)=0

(4)

容易看出这是无约束优化问题(λ视为参数)

(5)

的最优性条件，其中Lσk(x,λ)被称为增广的拉格朗日函数[1].最优化问题(5)有如下性质.

定理1[3]给定参数λ，假设x*是最优化问题(5)的最优解，则(x*,λ)是问题(1)的KKT对的充要条件是h(x*)=0.

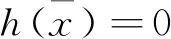
对比方程(4)与系统(2)可以看出，只有当h(x)=0时，由方程(4)才能得到系统(2).而在实际问题中，问题(5)的最优解同时满足h(x)=0的概率往往是很低的.下面这四个方法可以解决这个问题.

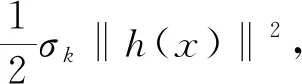
方法二：同时求解关于x与λ的如下无约束优化问题

(6)

该问题的最优性条件是

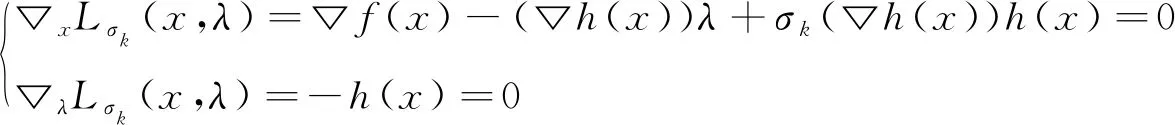
(7)

这与系统(2)是等价的.优化问题(6)的维度是m+l，比问题(1)的维度n增大了，因此对于约束比较多的等式约束优化问题，无约束优化问题(6)往往并不比原问题容易求解，尤其是当所求问题的维度比较大时.

对比系统(2)的第一个式子，可以利用λk+1=λk-σkh(xk)更新对偶变量λ.于是，得到拉格朗日乘子法

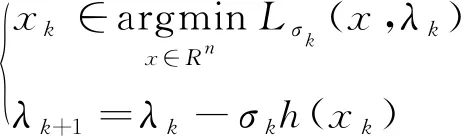
(8)

与(7)相比，拉格朗日乘子法(8)的优点是其交替的在原始空间Rn与对偶空间Rl中更新两个变量.这体现了分而治之的思想，将一个Rn+l维的问题分解为两个低维的子问题，这个优点随着问题维度的增加愈加明显.同时拉格朗日乘子法(8)在求解一些凸优化问题时有比较好的收敛结果[4].

方法四：如果约束条件是线性的，即h(x)=Ax-b，文献[5]提出了如下的定制拉格朗日乘子法

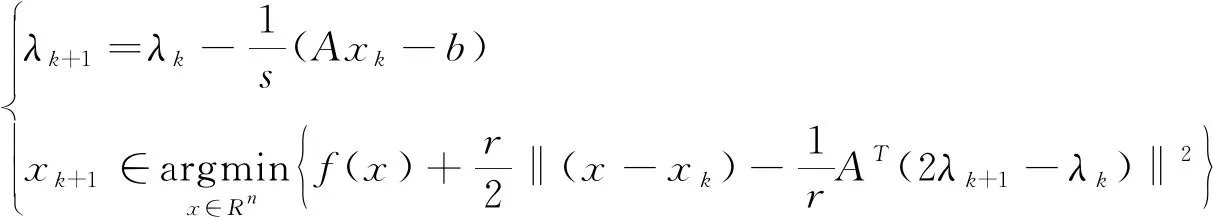
(9)

其中r>0,s>0,rs>‖ATA‖.关于迭代格式(9)，有如下收敛结果[5].

定理3[5]如果参数r,s满足r>0,s>0,rs>‖ATA‖，且f(x)是凸函数，则迭代格式(9)产生的点列{xk}全局收敛于问题(1)的一个最优解.

3 应用

例2 考虑约束最优化问题

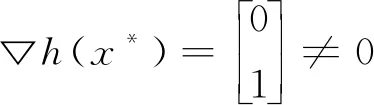
下面利用第2部分中的4种方法来求解该约束优化问题.

方法一：取一个充分大的罚因子，本例中取σk=106，并且给定λ=1.求解

根据无约束优化问题的一阶必要条件得

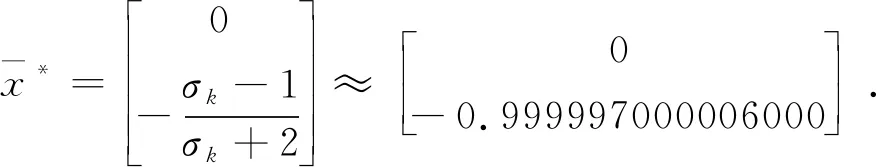
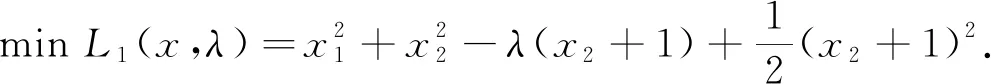
根据无约束优化问题的一阶必要条件得

方法三：给定λk，则由拉格朗日乘子法的迭代格式得

由无约束优化问题的一阶必要条件得

即

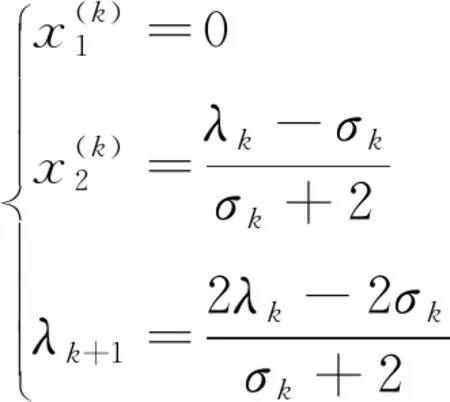
(10)

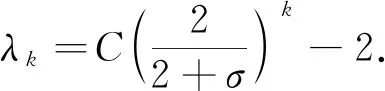
方法四：由迭代格式(9)得

由无约束优化问题的一阶必要条件得

(11)

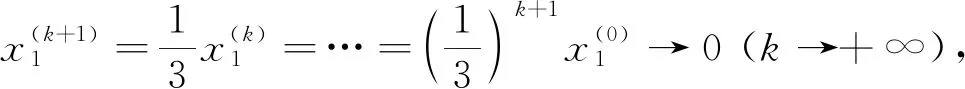
下面给出一个例子来说明拉格朗日乘子法可能失效.

例3 考虑约束最优化问题

解 类似于例2的求解过程，用拉格朗日乘子法求解上面的问题时得到如下迭代格式

(12)

显然当σ>0时，有|2/(2-σ)|>1，因此序列{λk}发散.由此可见，带固定罚因子的拉格朗日乘子法可能失效.

4 结语

本文讨论了拉格朗日乘子法的层次化教学模式：从引入拉格朗日乘子的必要性入手，给出了由目标到算法的反向设计思路，进而提出了四种基于增广目标函数的算法，并对算法的优缺点进行了分析.最后给出了实例详细说明了如何使用这些算法，举例说明了带固定罚因子的拉格朗日乘子法在求解非凸优化问题时可能失效.