基于时间序列的交通事故死亡人数集成预测探究*

李志成，王 珂

(1.安徽交通职业技术学院城市轨道交通与信息工程系，安徽 合肥 230001；2.兰州交通大学交通运输学院，甘肃 兰州 730070)

引言

近年来，我国城市化不断发展，机动车保有量和公路里程逐年增加，与此同时，我国的交通事故数量也在不断增加，其中事故死亡人数是大家的关注点之一.交通事故的发生具有随机性和不确定性，同时在特定的时空区域内又呈现出一定的规律性.基于此特性，为了进一步提高交通事故死亡人数的预测精度，国内外很多学者从不同角度对交通事故的各项指标进行分析和建模[1].

目前常用的交通事故预测方法有时间序列法、灰色预测、人工神经网络预测等[2].任英和王军雷等[3-4]分别建立交通事故面板模型，通过宏观和微观层面较全面的分析验证了该模型可以很好的应用于交通事故的相关因素分析中.王扬等[5]采用灰色系统理论对我国交通事故总量进行了预测.杜晓燕等[1]剖析事故次数和相关致因，并采用灰色度法求解其之间的关联度.张嘉琦和Xiao Kun Miao等[6-7]建立GM(1,1)模型预测了远期交通事故的数量.马国忠等[8]通过实例分析说明灰色-周期外延组合模型可用于交通事故死亡人数的动态预测.李相勇等[9]建立基于灰色预测方法的灰色马尔可夫预测模型提高道路事故的预测精度.乔向明[10]运用线性回归的方法建立11种预测方程模型，通过模型寻优预测31个省2004～2007年的交通事故死亡人数和直接经济损失的最优预测结果.沈坤和裘晨璐等[11-12]采用多元线性回归分析方法分别对交通事故影响要素进行了分析，建立交通事故预测回归模型，为国家宏观战略层次相关决策、预测提供参考.王祥等[13]利用非线性回归的方法预测全国道路交通事故发展形势，结果表明该方法简单易行且预测精度较高.朱茵[2]从公安交通管理的实际出发，提出基于非参数回归的道路交通安全趋势预测方法.Fagoyinbo等[14]利用最小二乘法来预测拉各斯州的道路交通事故总数和总人员死亡人数.孙浩和袁伟等[15-16]分别以我国机动车保有量、公路里程、人口、国民总收入等为参数，以我国交通事故死亡人数为基数建立最优组合预测模型，为提高预测精度提供理论依据.

此外，针对交通事故时间序列预测，国内外学者已开展了多方面研究，同时也颇有成效[17].例如:卢毅等[18]建立基于脉冲响应的城市交通协整模型，分析城市化与公共交通发展的内在联系，结果表明两者之间存在某种长期均衡关系.蒋宏等[19]针对北方某城市交通事故统计数据建立季节性时间序列模型，结果表明该模型能够充分利用历史数据从而减少误差，具有良好的适用性.邴其春等[20]构建的向量误差修正模型在预测交通事故时具有较好的预测效果.季彦婕等[21]建立道路交通事故多因素时间序列宏观预测模型，结果表明该模型具有数据资料少，建模简单，计算便捷的优点，能够很好的应用于道路交通事故预测.刘淼[22]选取2007～2012年的某城市交通事故四项指标数据，采用时间序列模型和灰色理论对道路交通事故次数和死亡人数进行了具体的预测，表明其结果是可信的.王文博等[23]从时间序列出发，构建了基于相关向量机(RVM)的交通事故预测模型，较好验证了1951～2013年的交通事故数.Chabok等[24]使用SARIMA模型分析评估过去几年的事故死亡趋势并预测未来4年的事故趋势，该模型被认为是预测死亡趋势的最佳拟合模型.Mutangi和Avuglah等[25-26]对于城市交通事故统计数据应用自回归综合移动平均(ARIMA)时间序列模型预测未来可能发生的年度交通事故数量.

综上所述，交通事故在时间序列上是具有一定的可预测性.因此，本文将以我国交通事故死亡人数为基数，采用VAR模型、ARMA模型、VEC模型分别进行预测，为提高交通事故的预测精度提供合理有效的理论依据.

1 时间序测模型简介

1.1 VAR模型及建模过程

当VAR模型对于相互联系的平稳时间序列变量是有效的预测模型，既可以做变量的指标分析，也可以做数据预测[27].

对于一个包含n个变量的p阶向量自回归模型，记为VAR(p)，其公式为:

Yt=c+A1Yt-1+…+ApYt-p+BXt+εt

(1)

式(1)中，Yt是k维内生变量向量，εt是k维扰动向量，Xt是d维外生变量向量，T是样本数量，k×k维矩阵A1,A2,…Ap和k×d维矩阵B是要被估系数矩阵，p为滞后阶数.

1.2 VEC模型及建模过程

对于不平稳变量，可以将数据取对数差分变为平稳变量，但这会改变其经济意义；若数据满足协整检验条件，用原始变量建立误差修正模型(VEC模型).VEC模型是VAR模型的一种，其建模一般是含有协整关系的非平稳时间序列[27].

向量误差修正模型可以表述为:

(2)

1.3 ARMA模型及建模过程

ARMA(p,q)模型是自回归滑动平均模型英文简称，该模型应用于单个平稳时间序列建模，模型包含了p个自回归项和q个移动平均项，其核心思想是要确定p和q这两个参数[28-29].其中，p决定了我们要用几个滞后时期的数据，而q决定了我们要用几个滞后时期的预测误差.ARMA(p,q)模型可以表示为:

Yt=φ1Yt-1+φ2Yt-2+…+φpYt-p+μt-θ1μt-1-θ2μt-2-…-θqμt-q

(3)

式(3)中，实参数φ1,φ2,…,φp称为自回归系数，θ1,θ2,…,θq称为移动平均系数，均为模型的待估参数.

1.4 综合集成预测方法

简单平均法和加权平均法是目前而言较为常见的综合集成预测方法.其中，简单平均法是以平均数为基础来确定数据预测值的方法，计算简便，适用于观测对象变化较小且没有明显趋势的情况.该方法表述为[28]：

(4)

但是简单平均预测法给每个预测模型分配相同的权重，对于模型的预测效果好坏并没有显示出明显的差异性，为了弥补该弊端，有些学者就提出了加权平均预测法.该方法根据每个预测模型的历史数据的优劣分配相应的权重，很好的体现了每个模型预测效果的好坏程度.该方法表述为:

(5)

(6)

式(6)中，|xi|为第i个模型的拟合误差或者预测误差的绝对值.

2 实例验证与分析

2.1 数据来源和选取

根据已有文献和数据的可获得性，本文选取中国1987～2017年的交通事故四项指标之一的事故死亡人数为研究对象.国民生产总值、总人口数、公路里程、机动车保有量分别为解释变量y1、y2、y3、y4，交通事故死亡人数为被解释变量y，变量均选取年度数据.图1描述了我国1987～2017年的交通事故死亡人数变化趋势，图2是交通事故死亡人数影响因素的变化趋势.文中各变量均来源于历年的国家统计局中国统计年鉴.

图1 我国1987～2017年的交通事故死亡人数图 图2 交通事故死亡人数影响因素图

2.2 VAR模型建模预测

2.2.1 单位根检验

本文利用Eviews软件对原序列进行单位根检验.单位根检验发现原序列t统计量的P值均大于0.05，这表明原序列为非平稳序列；所以对原序列进行ADF检验，结果如表1所示.可以得出，二阶差分后序列平稳，且为二阶单整.

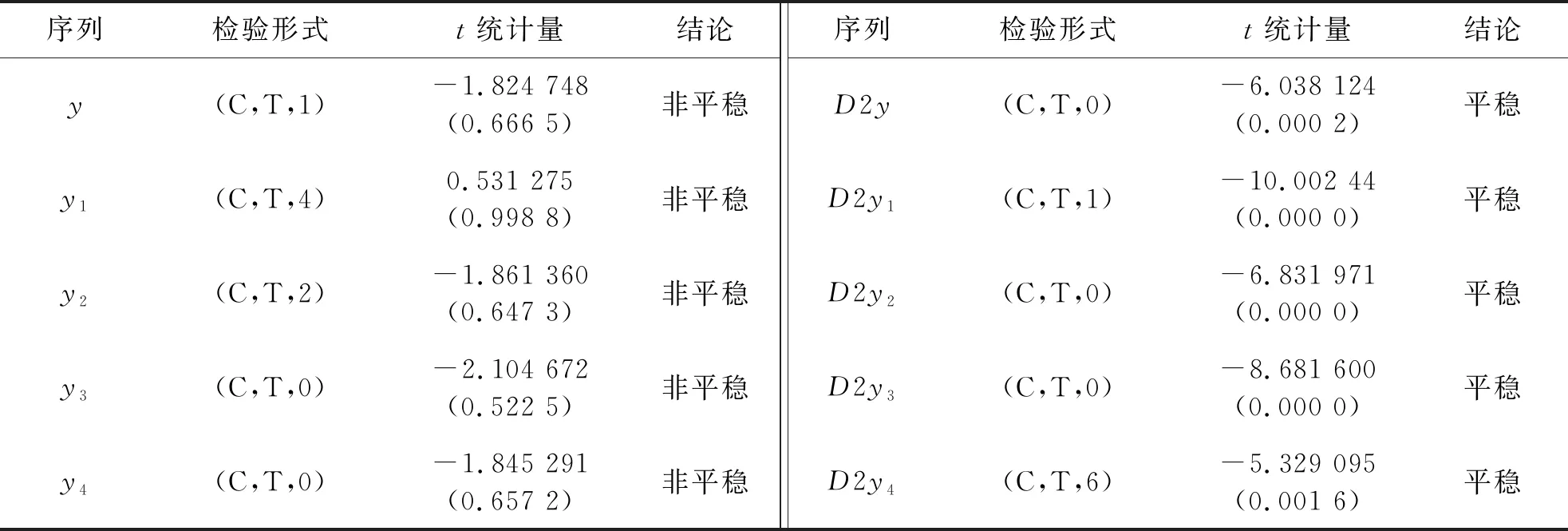
表1 平稳性检验表

2.2.2 确定最佳滞后阶数并建立VAR模型

在确定VAR模型的最佳滞后期时，综合考虑评价指标LR、FPE、AIC、SC和HQ的值，结果如表2所示.从表2可以得出，滞后阶数为2时评价指标的“*”号最多，因此将模型的最优滞后阶数选择为2，即建立VAR(2)模型.

表2 VAR模型滞后期的5个指标评价值

2.2.3 VAR模型检验

由图3可以得出，VAR(2)模型的特征根全部落在单位圆曲线内，这表明建立的VAR(2)模型是稳定.

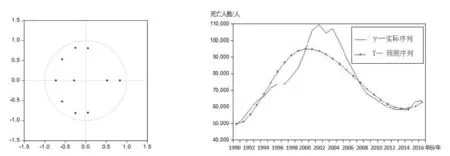
图3 VAR(2)模型单位圆曲线图 图4 VAR(2)模型对交通事故死亡人数拟合预测和实际值对比图

2.2.4 VAR模型预测结果

由图4可以得出，1990～2000年之间预测值在原序列附近上下浮动，2000～2008年两序列差值较大，之后又趋于近似.

2.3 VEC模型建模预测

2.3.1 Johansen协整检验

若序列非平稳，存在协整关系，且为同阶单整，则可以建立VEC模型.根据表1得出y1、y2、y3、y4这四个因素的时间序列值二阶差分经ADF单位根检验是平稳的，可以采用VEC模型.

Johansen协整检包括迹检验(Trace test)和最大特征根检验(Max-eigenvalue)，目的是为了防止伪回归现象的出现.从表3可以得出，这两种检验结果均显示在5%显著水平下存在2个协整关系，表明y和y1、y2、y3、y4之间存在长期均衡关系，因此可以通过y1、y2、y3、y4对y未来的变动趋势进行预测.

表3 Johansen协整检验

2.3.2 VEC模型建立

经过协整关系检验，发现存在协整关系，对交通事故死亡人数进行VEC建模，模型拟合效果一般， 1990～2017年的交通事故死亡人数VEC建模预测的拟合效果如图5所示.

图5 VEC模型对交通事故死亡人数拟合预测和实际值对比图 图6 自相关及偏自相关图

可以得出，1990～2000年之间预测值与实际值具有相同的发展趋势，预测效果较好，2000～2017年之间预测值波动较大，预测效果较低.

2.4 ARMA模型建模预测

2.4.1 平稳化处理

为判断交通事故死亡人数的数据的平稳性，将1987～2017年的历史数据定义为随机序列y，且序列y是一个不平稳的时间序列，结果如表4所示，ADF检验表明，一阶差分序列平稳，因此可以对其构建ARMA模型.

表4 交通事故死亡人数平稳化处理

2.4.2 模型识别与建立

根据图6自相关和偏自相关图观察ACF和PACF，发现偏自相关系数截尾，自相关系数缓慢递减且基本位于2倍标准差范围内.为了进一步确定ARMA模型，通过建立相应的估计方程，根据ACI，SIC最小准则确认建立AR(2)模型，并得到模型AR(2)的拟合结果如表5所示.拟合结果中，AR(1)和AR(2)的P值远小于0.05，证明该模型的拟合效果最为理想.

表5 AR(2)模型拟合结果

2.4.3 模型检验

通过残差分析试验来检验模型，本文基于AR(2)模型拟合结果的ACF和PACF确定残差序列的独立性，结果见表6.表6中残差诊断滞后一阶，Q-stat的P值=0.324 0> 0.05，拟合模型残留误差接受于白噪声，残差无序列相关，表明无遗漏变量.这在一定程度上体现了AR(2)模型交通事故死亡人数信息的充分性，因此该模型是适合的模型.

表6 AR(2)模型残差诊断

2.4.4 模型预测

为检验模型的预测效果，采用静态预测的方法，预测1990～2017年的交通事故死亡人数，并与实际情况比较，如图7所示.可见，短期预测值与实际值的趋势基本一致，预测结果良好，但整体还有一定的偏差，在预测精度上仍有很大的提升空间.

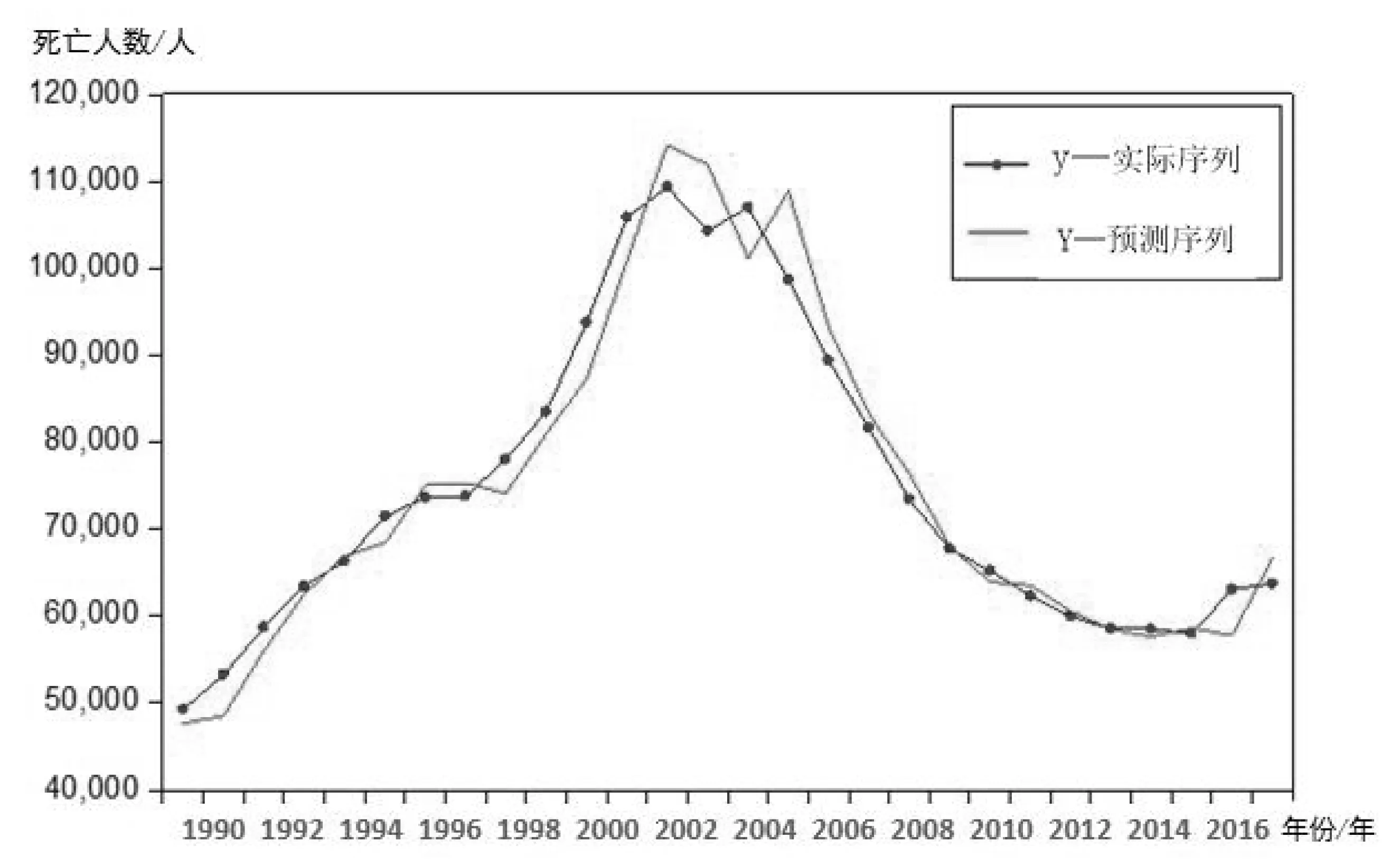
图7 ARMA模型对交通事故死亡人数拟合预测和实际值对比图

2.5 三种预测模型的预测结果

用VAR模型，VEC模型，ARMA模型分别对交通事故死亡人数进行预测，结果如表7所示，可见，VAR模型在三年的预测中表现出较高的稳定性，其平均误差为-1.71%.而VEC模型预测效果最差，2015年误差较大，为19.9%，其三年平均误差高达16.48%.ARMA模型虽然在2016年的预测中达到-7.87%的误差，但其三年平均误差在10%以内，预测效果良好.整体而言，三种模型预测2015～2017年的交通事故死亡人数呈现平稳上升的趋势，这与实际趋势相符合.不过，单个预测模型的误差仍然相对较大，容易出现不可靠因素，因此对我国交通事故死亡人数提出综合集成预测的方法.

表7 三种模型预测结果与实际值的误差率

2.6 综合集成预测

由表7得出VEC模型预测误差较大，不宜加入综合集成预测，对VAR和ARMA模型进行集成，通过计算，两种模型的集成预测权重结果如表8所示.根据1.4节提出的综合集成预测方法计算出2015～2017年的交通事故死亡人数，结果及误差如表9所示.

表8 集成结果权重分配

可以看出，综合集成预测误差较低，误差波动较小，预测效果较好，很好的避免了单个模型预测的局限性.此外，为了比较样本外模型的预测效果，采用动态预测的方法分别预测了2018～2020年的交通事故死亡人数如表9所示.从整体上看，事故死亡人数仍然呈现出稳定上升趋势.

表9 交通事故死亡人数预测值及集成结果

3 结论

本文分别建立VAR，VEC，ARMA三类模型来预测我国交通事故死亡人数.其中，VAR和ARMA模型的预测效果良好，而VEC模型有待改进.最后提出交通事故死亡人数的VAR和ARMA模型的综合集成预测，通过计算得出，综合集成预测的精度和稳定性较高.因此，综合集成预测能够有效提高我国交通事故死亡人数的预测精度，这对于交通预测有着很重要的借鉴意义.