一类二阶有理差分方程动力学定理的证明*

全卫贞,李晓培,凌伟钟,阿的史古,陈月婷，全国标

(1. 湛江幼儿师范专科学校数学系，广东 湛江 524037；2. 岭南师范学院基础教育学院,广东 湛江 524037)

1 预备知识

考虑二阶有理差分方程

(1)

式中初始值x-1,x0∈(0,+∞)，p,q,r>0，n=0,1,2,…．

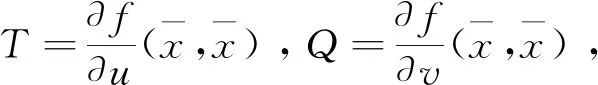
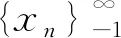
1)f(x,y)关于x单调递增，关于y单调递减；

2)若有f(m,M)=m和f(M,m)=M，则m=M．

1)f0(x,y)和f1(x,y)关于x不增，关于y不增；

2)f0(x,x)>0，(x≥0)；

3)f0(x,y)+f1(x,y)<1,x,y∈(0,+∞)．

2 定理及其证明

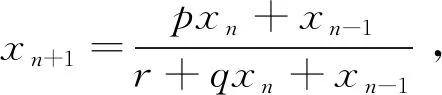
若f(m,M)=m，f(M,m)=M，即

则有

rm+qmM+m2=pM+m，rM+qmM+M2=pm+M．

将这两个式子相减得 (m-M)(m+M+r+p-1)=0. 又由于p+1≤r，m>0,M>0，即

m+M+r+p-1>0，所以m=M.

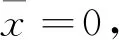
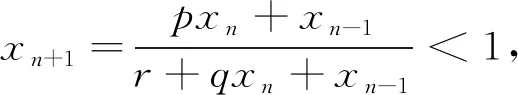
f(x,y)在[0，1]上关于x单调递增，关于y单调递减．所以有

由上面两个不等式得pI+S-Ir-qI2≤IS≤pS+I-Sr-qS2，即

(I-S)[1+r-p+q(I+S)]≥0．

因p+1≤r，S>0，I>0 ，所以1+r-p+q(I+S)>0．又因为S≥I，所以S=I，由此可得，

方法3 由

f0,f1：(0,+∞)×(0,+∞)→(0,+∞)，且满足：

①f0(x,y),f1(x,y)分别关于每个变量都是单调递减的；

②对于所有的x≥0，f0(x,x)>0始终成立；

③又因为p+1≤r，对所有的x,y∈(0,∞)，都有

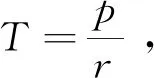
进一步，当1-p

1)当q+r>3p+1+qr+pq时，将这个不等式整理可得q-p+r>2p+1+qr+pq>0，即

Q>0，T2+4Q>0，q-p-qr>2p+1+pq-r=(p+1-r)+p+pq>0，所以T<0.

当p+1>r时，

2)当q+r<3p+1+qr+pq时，由T<0可得

即|T|<|1-Q|.

若T>0，由p+1>r可得

证明若方程(1)存在素二周期解{…,φ,φ,φ,φ,…}，且φ≠φ，则方程(1)必须满足

整理上式得 (φ-φ)(φ+φ+r+p-1)=0.于是由φ≠φ知，φ=1-r-p-φ.将其代入

rφ+qφφ+φ2=pφ+φ，得

rφ+qφ(1-r-p-φ)+φ2=p(1-r-p-φ)+φ.

反之亦然. 证毕.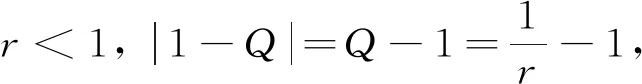

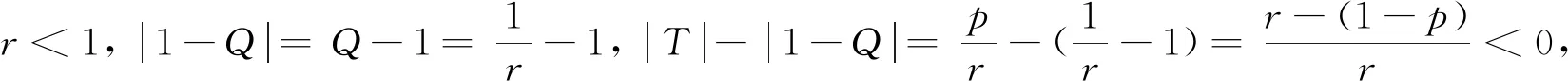
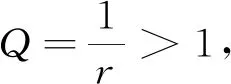
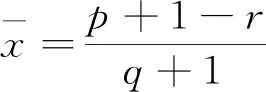
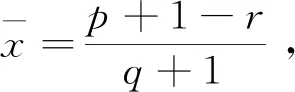
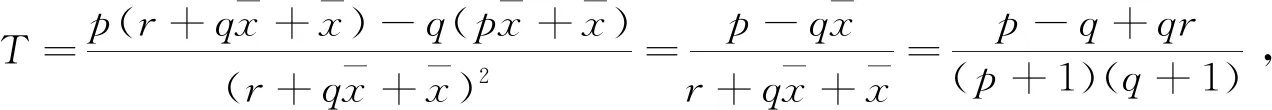
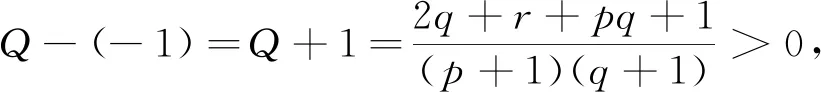
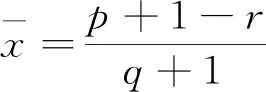
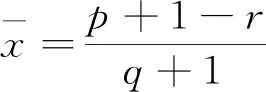
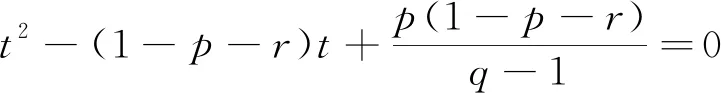
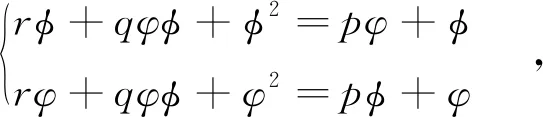
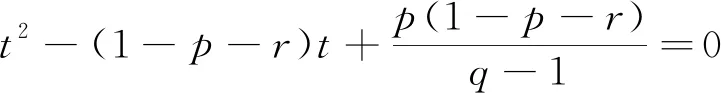
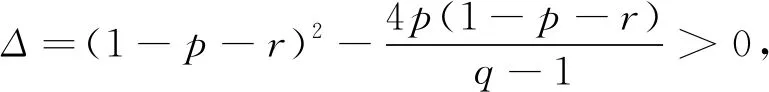
3 结语