草木沟隧道温度场实测与分析

2022-05-19丁云飞高焱包旭王仁远李慧

科学技术与工程 2022年12期

丁云飞，高焱，包旭，王仁远，李慧

(1.南京工业大学交通运输工程学院，南京 211800； 2.淮阴工学院交通工程学院，淮安 223003；3.石家庄铁道大学土木工程学院，石家庄 050043)

随着“交通强国”发展战略的深入，中国铁路网结构的日益完善，隧道工程正向着高纬度、高海拔等气候条件恶劣的严寒地区延伸[1]。严寒低温引发的隧道衬砌冻胀、开裂、掉块、道床结冰等病害，严重影响列车行驶安全，给铁路运行带来巨大的损失。因此，开展寒区隧道温度场的研究，对解决寒区隧道冻害问题显得十分重要。

近年来，中外学者针对寒区隧道温度场进行了大量的研究。赖远明等[2]提出了寒区隧道温度场圆形截面的解析解，为寒区隧道冻结问题及工程估算奠定理论基础；Liu等[3]基于圆形隧道围岩冻胀压力的弹性模型、断裂力学和细观损伤理论，提出了冻融循环条线下围岩弹性模量降低和岩石孔隙比增加的冻胀压力模型，该模型可用于计算围岩冻胀压力随冻融循环次数的变化；冯强等[4]采用Laplace积分变换的方法得到了寒区隧道保温层、衬砌和围岩温度的解析解，为寒区隧道衬砌、保温层厚度等设计参数提供计算方法；Zhang等[5]以青海省大阪山隧道为依托，利用大型有限元软件模拟冻融环境下隧道热湿耦合的温度场变化规律；王仁远等[6]以京张铁路正盘台隧道为研究对象，利用ANSYS有限元软件，研究了不同围岩温度、入口风速和冻结时长条件下隧道温度场的变化规律；高焱等[7]以祁连山隧道为依托，分析了有无保温层情况下隧道温度场的变化规律；张晨曦等[8]结合中国26座寒区隧道洞内温度实测数据，采用理论分析和数值模拟的方法研究了热位差及洞口净压差对寒区隧道温度场影响；郑余朝等[9]以京沈高铁瓦房店隧道为依托，研究了隧道入口处风的温度、方向、速度和时间变化对温度场的影响；赵希望等[10-11]通过对榆树川隧道温度实测数据分析下，确定了隧道进出口端的设防长度，同时综合考虑水-热耦合对衬砌-围岩热传导的影响，建立寒区隧道围岩冻结过程中水-热耦合模型，确定了隧道严重冻害的具体位置和时间；陈建勋等[12]对某寒区隧道温度场进行了长期的现场实测，揭示了寒区隧道温度场的变化规律；叶朝良等[13]通过对中国35座寒区隧道温度实测数据的分析，给出了隧道保温段设防长度的计算公式。以上学者的研究成果不仅为寒区隧道温度场的研究提供了丰富的理论基础，同时也为寒区隧道的施工及维护提供了大量的数据指导。但当隧道运行后，由于隧道洞内外温差及列车运行的影响，隧道外寒冷气流受温差及列车运行的作用侵入隧道内部，进而改变隧道围岩温度场的分布情况，因此要准确分析某一隧道温度场的分布规律及防寒措施时，除了对隧道内在因素的分析，更需要考虑列车运行等外界因素的影响。

吉图珲铁路客运专线是振兴东北老工业基地和完善铁路网布局的重要组成部分。铁路沿线为重度季节冻土区，全年冻结期高达6个月，全线隧道面临着季节性冻融、侧壁挂冰、排水沟冻结和隧底上鼓等冻害问题。草木沟隧道作为吉图珲铁路客运专线的重点控制性工程，研究其不同冻结期、不同外界温度和列车运行等情况下围岩温度场分布规律对隧道施工和解决隧道冻害问题具有重要意义。

1 草木沟隧道工程概况

1.1 隧道概况

草木沟隧道位于吉林市龙潭区江密峰镇草木沟村境内，是新建吉图珲铁路客运专线重点控制性工程之一，列车设计时速250 km，隧道全长3 413 m，设计围岩Ⅱ、Ⅲ、Ⅳ、Ⅴ级围岩，其中包括浅埋地段，地下水发育，岩体稳定性差，开挖易出现掉块、坍塌等现象，地质条件极为复杂。

草木沟隧道处于东北严寒地区，为重度季节冻土区。隧道地区属于北亚温带湿润半湿润大陆性季风气候，春季干旱多风，夏季短促温暖，秋季凉爽，冬季漫长酷寒。据2020年监测数据显示，隧道外界年最高气温为33.8 ℃，年最低气温为-29.01 ℃，每年从10月开始冻结，翌年4月开始融化；年降雨量528～670 mm，主要集中在6—8月；全年平均风速为2.2 m/s，主导风向与隧道走向一致，即进口(阴坡)迎风，出口(阳坡)背风。隧道外界气温时间曲线如图1所示。

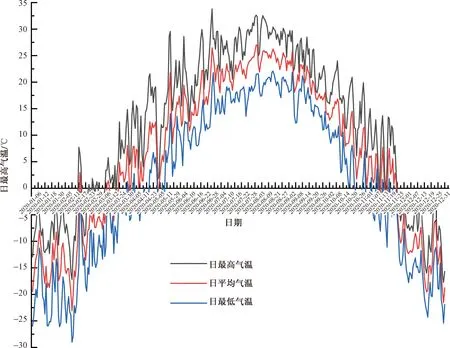
图1 草木沟隧道外气温时间曲线Fig.1 Temperature time curve outside Caomugou Tunnel

1.2 实测方案

隧道温度测试断面里程分别为DK026+000、DK025+925、DK025+818、DK025+730、DK025+600、DK025+470、DK025+320和DK025+160,共计8个断面。每个断面布置12个温度传感器、2个温度采集仪表和2个数据管理主机；12个温度传感器安装在距地面高度1 m和5 m测温孔内(测温孔直径Φ40 mm)，温度传感器具体布置于二衬表面、初衬表面、60、120、180分别240 cm处。断面测温传感器分布及各断面位置如图2、图3所示。

图2 断面传感器分布示意图Fig.2 Schematic diagram of section sensor distribution

图3 断面位置示意图Fig.3 Schematic diagram of section position

试验采用的现场测试设备包括温度传感器、温度采集仪表、数据管理主机和电源控制箱。数据管理主机通过总线电缆连接对温度采集仪表进行管理，并自动进行数据采集、转储。隧道测温仪表现场安装如图4所示。

图4 隧道测温仪表现场安装图Fig.4 Field installation drawing of tunnel thermometer

1.3 隧道温度实测

2013年4月1日—2014年3月31日对草木沟隧道进行了长期的现场温度实测，温度采集仪表每小时采集一次数据，每组数据包括2个衬砌表面和10个围岩温度，每个断面共测得8 688组数据，为方便观察选取具有代表性的DK026+000断面处6：00左右数据进行分析。DK026+000处温度实测数据及温度拟合曲线如图5所示。

图5 DK026+000处实测数据及拟合曲线Fig.5 Measured data and fitting curve at DK026+000

由图5可知，草木沟隧道实测数据拟合曲线温度变化符合正弦规律变化。2013年10月—2014年4月中旬隧道洞内壁面温度始终低于围岩温度且围岩距离洞壁越远温度越高，深部围岩温度呈逐渐下降的趋势，温度下降曲线比较平缓；4月下旬—9月隧道洞内壁面温度始终高于围岩温度且围岩距离洞壁越远温度越低，洞壁表面温度呈波动上升的趋势，温度上升曲线波动较大；隧道冻结期达4个月，冻结期平均最低气温为-9.53 ℃；年最低气温为-20.6 ℃，年最高气温为23.12 ℃，隧道DK026+000处由二衬表面至径深240 cm处的温度振幅分别为16.94、11.39、7.68、5.72、4.61、3.72 m。

2 寒区隧道温度场理论计算模型

寒区隧道发生冻害的主要原因是隧道洞外寒冷空气侵入隧道内部，冷空气与隧道内空气及围岩进行热交换，使得隧道内部温度低于0 ℃；加之“十隧九漏”的现象长期存在于隧道中，低温致使隧道结冰导致衬砌冻裂、挂冰等冻害问题[14]。因而，寒区隧道温度场理论计算模型大体分为隧道洞内空气对流换热和围岩传热两部分。

2.1 隧道内空气对流-导热方程

隧道洞内流体对流换热问题本身十分复杂。为了简化对流换热问题的计算方法，做出以下假设[15]：①隧道内气流为不可压缩的理想流体；②隧道内气流流动状态为层流；③隧道内气流密度为常数；④隧道进出口边界条件为压力进出口边界条件且气流压力不随温度的变化而变化。隧道内流体对流换热遵循以下三种基本守恒定律方程[16]。

2.1.1 质量守恒方程

质量守恒定律表示为单位时间内隧道内空气流体微元体中质量的增加量等于同时间内流入该微元体的净质量。质量守恒方程的一般形式为

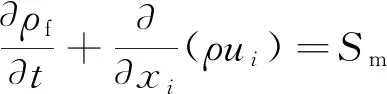
(1)

式(1)中：ρf为流体密度，kg/m3；t为时间，s；ui为i方向上的速度，m/s；xi为i方向的坐标；Sm为源项，取0。

2.1.2 动量守恒方程

动量守恒定律表示为微元体中流体的动量对时间的变化率等于外界作用在该微元体上的各种力之和。动量守恒方程为

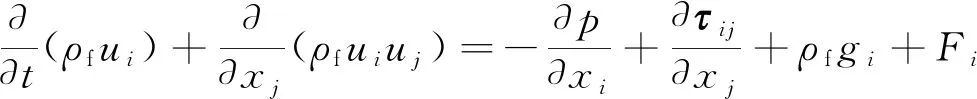
(2)

(3)

(4)

式中：p为静压，Pa；μ为流体黏度，Pa·s；xj为j方向的坐标；τij为应力张量；gi和Fi分别为i方向上的重力体积力和外部体积力；δij为克罗内克符号。

2.1.3 能量守恒方程

能量守恒定律表示为微元体中能量的增加率等于进入微元体的净热流量加上体积力与表面力对微元体所做的功。能量守恒方程为

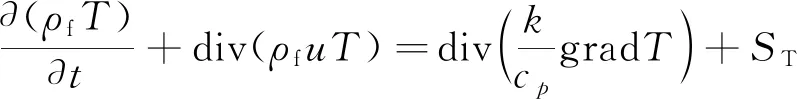
(5)

式(5)中：cp为比热容，kJ/(kg·K)；T为温度，K；k为流体的传热系数，W/(m·K)；u为流体速度，m/s；div为散度；grad为梯度；ST为黏性耗散项。

2.2 隧道围岩导热方程

为简化隧道围岩内部热传导计算，做出以下假设：①隧道围岩为均质材料且各项同性；②围岩表面与隧道洞内空气充分接触；③隧道洞内流速、热力学参数恒定。围岩热量变化量方程为

(6)

式(6)中：T0为初始温度， ℃；ρ为材料密度，kg/m3；λ为围岩导热系数，W/(m·K)；Cp为围岩的比热容，kJ/(kg· ℃)。

考虑围岩地温、气流速度和气流温度的计算方程为

(7)

式(7)中：h为围岩-空气对流换热系数，W/(m2·K)；Tw为隧道围岩温度， ℃。

由式(7)可知，隧道围岩传热过程受到围岩地温、围岩导热系数、围岩比热容、围岩基本物理量和围岩-空气之间对流换热系数等参数共同影响。

3 草木沟隧道温度场分析

3.1 有限元计算模型

有限元法的应用是将求解域看成是由许多称为有限元的小互连子域组成，对每一单元假定一个合适的近似解，然后推导求解这个域总的满足条件。有限元不仅计算精度高，而且能适应各种复杂形状，是寒区隧道温度场的有效分析手段。

草木沟隧道施工过程中，隧道围岩温度场因开挖等外界作用遭受严重破坏；同时隧道贯穿后，原有温度场的平衡被打破，隧道围岩和衬砌受寒冷气流及季节性气温冻融持续影响，隧道衬砌结构遭受了不同程度的破坏。为简化计算模型，采用有限元软件计算隧道温度场过程中做如下假定：①假定隧道衬砌及周边围岩均为均质、各项同性材料；②假定计算模型达到一定埋深后，其围岩原始地温沿深度方向保持不变；③假定边界条件采用固体壁面边界，其中热传导系数、比热容、密度、空气对流换热系数等热力学参数均为常数。

利用ANSYS建立草木沟隧道等比例计算模型，隧道围岩长宽设置为100 m，z轴为进深方向，隧道进深为3 413 m，共划分146 880个单元和155 550个节点，未设置保温层等保温结构，隧道网格划分如图6所示。

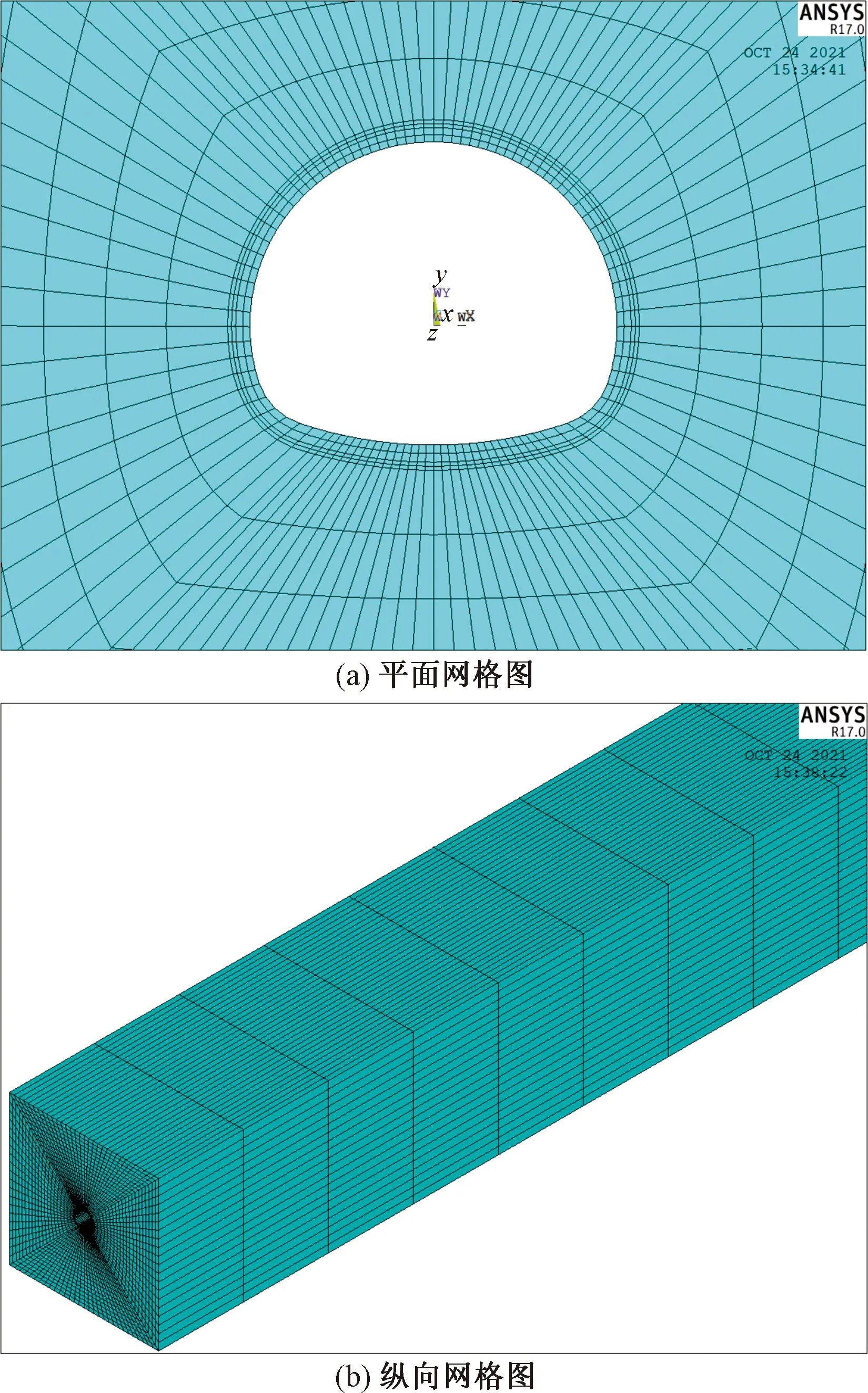
图6 隧道网格划分Fig.6 Tunnel meshing

3.2 计算参数

草木沟隧道贯穿后，隧道温度场的变化主要受到混凝土衬砌与外界寒冷气流的热交换影响。因此，数值模拟中衬砌-空气之间的对流换热系数不容忽视；张建荣等[17]通过风洞实验提出混凝土表面空气对流换热系数hc的计算公式为

hc=3.06v+4.11

(8)

式(8)中：v为风速，m/s。

由式(8)可知，草木沟隧道自然风速下的对流换热系数为10.842 W/(m2·℃)。其他相关计算参数如表1所示。

表1 计算参数

3.3 数值模拟验证

以吉珲铁路草木沟隧道实测数据进行数值模拟验证。实测值与数值模拟值如图7所示。

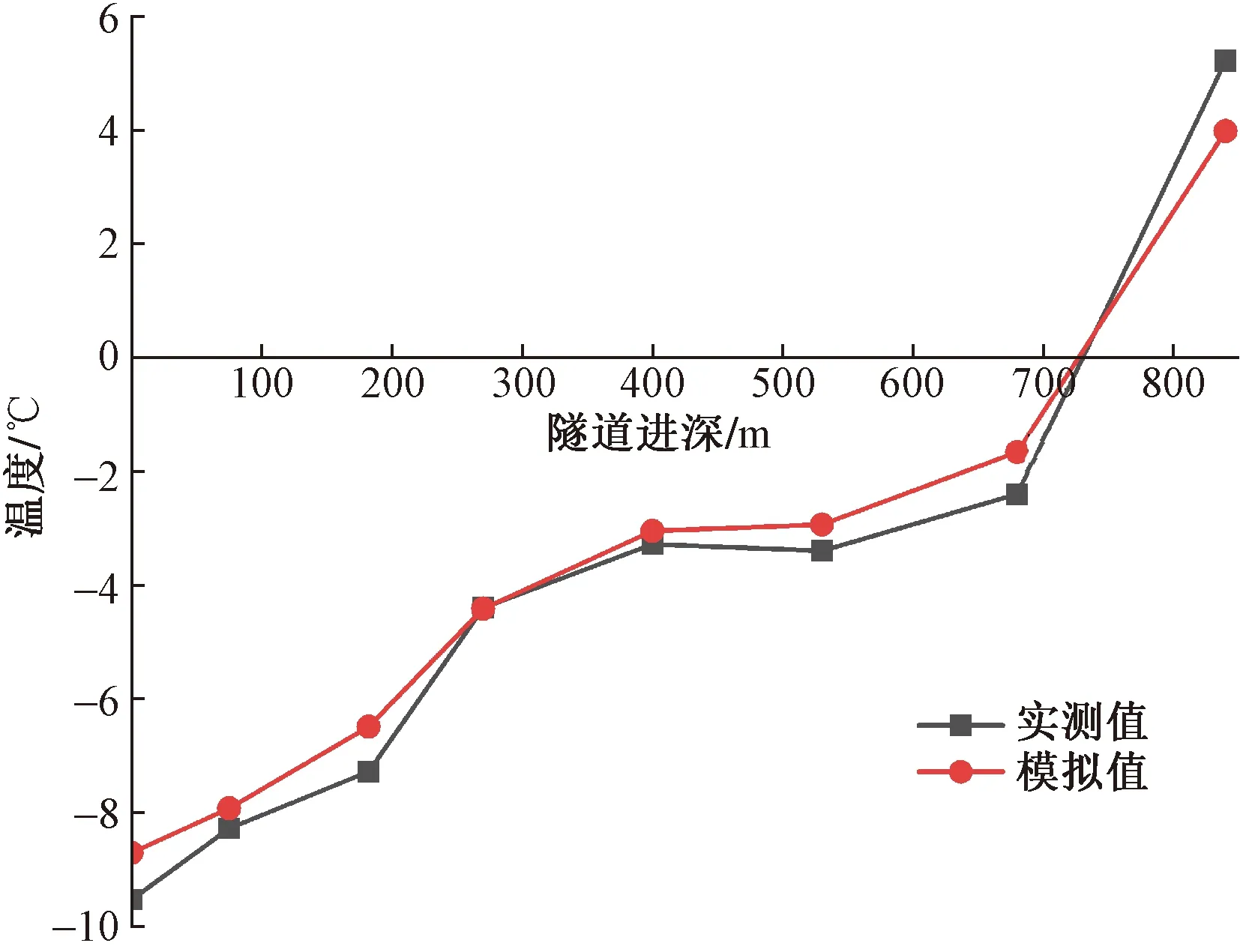
图7 洞内温度实测值与模拟值分布规律对比Fig.7 Comparison of distribution law between measured and simulated temperature in tunnel

由图7可知，模拟值与实测值温度变化规律基本一致，隧道温度随着进深长度的加深而升高；平均误差为0.58 ℃，满足工程数值模拟计算误差需求。

3.4 不同条件下温度场的影响规律

隧道洞外气温、风流速度和冻结时长是影响草寒区隧道温度场的主要外界因素；隧道围岩地温、隧道尺寸和材料属性是影响寒区隧道温度场的内在因素。因此，草木沟隧道温度场的分析采用控制变量法；固定隧道尺寸、围岩地温和材料属性等内在因数；针对不同冻结时长、风流速度和洞外气温等外在因数进行数值模拟分析。

3.4.1 不同冻结期温度场的变化规律

采用有限元软件计算年最冷日气温下隧道围岩温度场。计算中建立等比例草木沟隧道模型，外界气温设置为-9.53 ℃，围岩地温设置为7.5 ℃，采用隧道外自然风条件下的对流换热系数，不考虑列车风等极端风速条件。分别计算30、60、90、120 d冻结期下温度场的变化规律。不同冻结期温度场的变化规律如图8所示。

由图8(a)～图8(d)可知，草木沟隧道30、60、90、120 d冻结期下的洞口壁面温度分别为-8.39、-8.65、-8.74、-8.79 ℃，隧道30、60、90、120 d冻结期下洞口段径向冻结深度分别为2.45、3.38、4.19、4.89 m，冻结时长每增加30 d壁面温度平均降低0.13 ℃、冻结深度平均增加0.81 m；随着冻结期的增加，围岩温度降低，其空间分布规律与原始围岩基本一致。围岩越靠近衬砌，其温度分布越接近隧道洞内气温；沿径深方向，围岩温度随着径向距离的增加而增加，其温度曲线逐渐趋于平缓，在距衬砌25 m处断面的围岩温度与围岩地温基本一致。产生上述变化规律的原因主要是随着隧道冻结期的延长，洞外寒冷气流与隧道壁面进行长时间的对流换热，从而使得隧道壁面的温度持续降低，长期的冻胀作用下严重影响衬砌结构安全和行车安全。

由图8(f)可知，在3 413 m长隧道中仅有280 m温度处于0 ℃以上，0 ℃以下的纵向距离没有随冻结时间的增长而有明显的变化。因此，应对草木沟隧道全长采用防寒保温措施。

3.4.2 不同外界温度条件下温度场的变化规律

由草木沟隧道外气温时间曲线(图1)可知，隧道外界年最低温度可达-29.01 ℃。固定围岩地温为7.5 ℃，分别计算外界气温为-30、-25、-20、-15、-10 ℃条件下草木沟隧道冻结期内温度场的演化规律。因隧道进深仅有3 413 m，气温为-9.53 ℃情况下隧道温度基本均低于0 ℃，因此不考虑纵向温度场在不同外界气温下的变化。不同外界气温条件下洞口处径向温度场的变化规律如图9所示。

图9 不同外界温度条件下温度场径向变化规律Fig.9 Radial variation law of temperature field under different ambient temperature conditions

由图9可以看出，隧道洞口处径向温度变化随着距离的增加逐渐趋于平缓，直至达到围岩地温；随着外界气温的降低，冻结深度逐渐增加，外界温度为-10、-15、-20、-25、-30 ℃时冻结深度分别为4.9、6.1、6.9、7.7、8.2 m；外界温度每降低5 ℃，冻结深度平均增加0.825 m。由此可见，外界环境温度对隧道冻结深度的影响较大。

3.4.3 不同风速条件下温度场的变化规律

隧道运行期间，列车风会改变隧道内自然风的风速，对隧道内的温度场影响很大。根据《铁路隧道运营通风设计规范》(TB 10068—2010)[18],双线隧道通风设计中自然风速可按2.0 m/s计算。列车风速vm的计算公式为

(9)

(10)

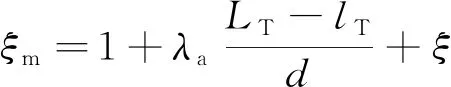
(11)

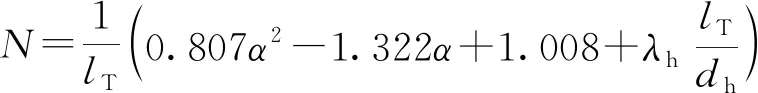
(12)

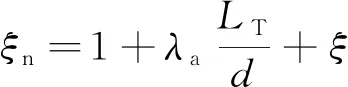
(13)

式中：Km为活塞风作用系数；ξm为隧道段除环状空间外的阻力系数；N为列车阻力系数；λa为隧道平均摩擦系数；LT为隧道长度，m；lT为列车长度，m；d为隧道断面当量直径；ξ为隧道入口阻力系数；ξn为隧道的总阻力系数；vn为隧道内自然风速，m/s；α为阻塞比，是列车断面积与隧道断面积比值；vT为列车速度，m/s；λh为列车平均摩擦系数；dh为列车断面当量直径。

由式(9)计算可得，列车运行速度为250、200、160、140 km/h时，列车风速度分别为22.47、17.95、14.32、12.51 m/s。由式(8)计算可知，对流换热系数分别为72.86、59.03、47.94和42.38。固定围岩地温为7.5 ℃，分别计算列车运行速度为250、200、160、140 km/h时草木沟隧道温度场的演化过程。不同列车运行速度下洞口处温度场的变化规律如图10所示。

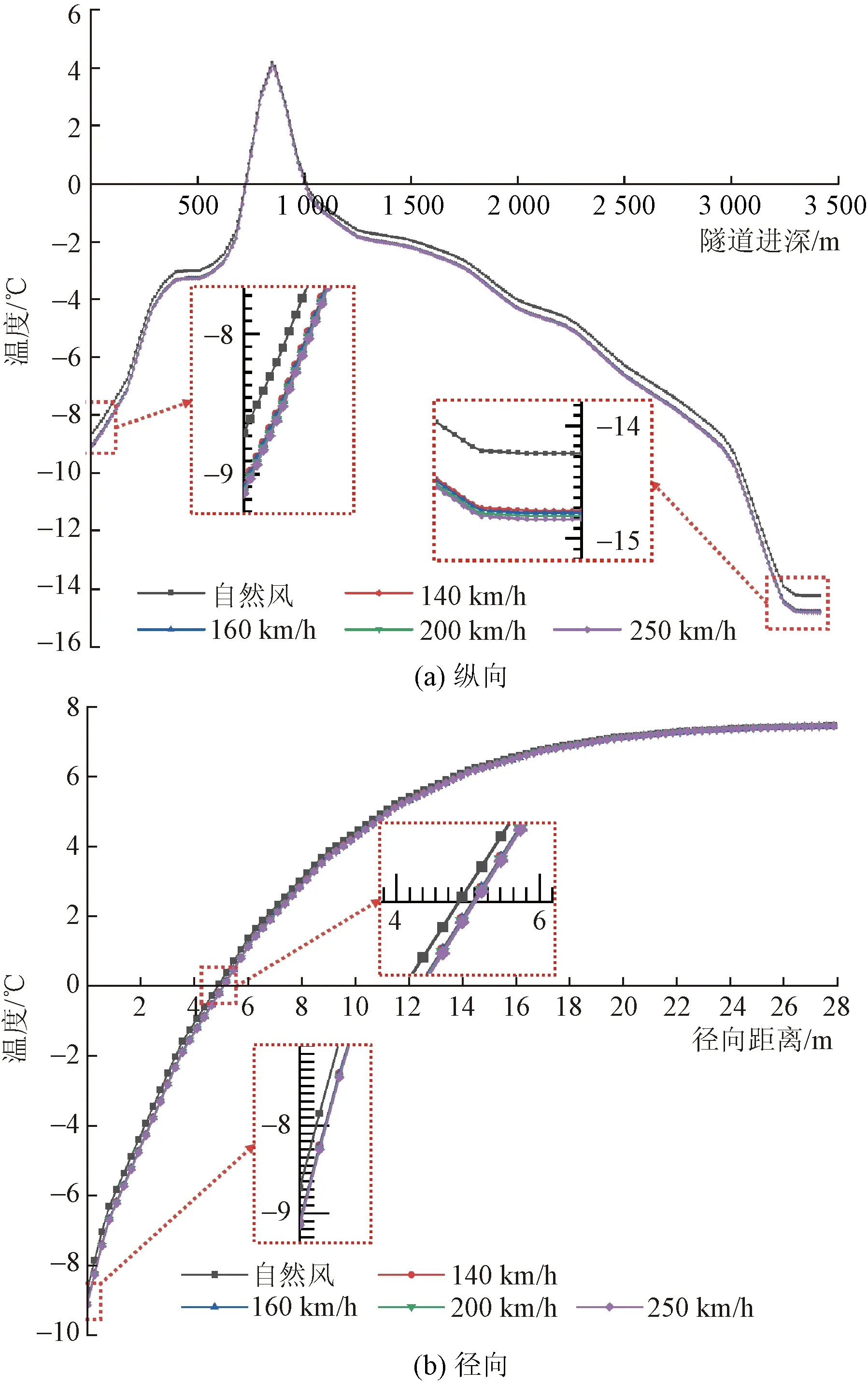
图10 不同列车风运行条件下温度场变化规律Fig.10 Variation law of temperature field under the conditions of different train running wind

由图10可知，受列车风的影响隧道进出口处围岩温度相较于自然风情况下分别平均下降了0.4 ℃和0.54 ℃，隧道洞口处径向冻结深度相较于自然风情况下平均增加了0.19 m；列车风的存在增加了风流与衬砌之间的对流换热，虽然在3 413 m长草木沟隧道中列车时速的增长对中隧道温度场的影响较小，但列车风对隧道冻害的影响不容忽视。