空间耦合低密度奇偶校验码的深度迭代译码算法设计
2022-05-19刘欣刘洋王斌张育芝
刘欣, 刘洋, 王斌, 张育芝
(西安科技大学通信与信息工程学院, 西安 710054)
空间耦合低密度奇偶校验(spatially coupled low density parity check,SC-LDPC)码作为一种能够证明可达容量限的编码方案而受到中外学者的广泛关注。SC-LDPC码由Kudekar等[1]于2011年首次提出,并证明了当码长足够长时,SC-LDPC码在二元删除信道(binary erasure channel, BEC)下采用置信传播(belief propogation, BP)译码算法可获得接近于相应分组LDPC码采用最大后验概率(maximum a posterior, MAP)译码算法时的性能,即SC-LDPC码具有“阈值饱和”特性。之后,Kudekar等[2]还证明了SC-LDPC码在二进制无记忆对称(binary memoryless symmetric, BMS)信道下也存在“阈值饱和”现象。然而,SC-LDPC码优异的“阈值饱和”特性需要在码长很长时才能实现,当采用BP译码算法时,实现复杂度呈指数倍增加,无法在实际中应用。Iyengar等[3]、Ali等[4]提出了将滑窗译码算法应用于SC-LDPC码译码,开启了SC-LDPC码滑窗译码算法性能和译码复杂度的研究。除滑窗译码算法外,Bazzi等[5]将线性规划译码算法引入SC-LDPC码的译码上,用于分析和证明SC-LDPC码集的阈值饱和特性。上述关于SC-LDPC码的译码算法研究主要集中于实现译码复杂度和译码性能之间的有效折中。
近年来,深度学习技术在各个领域均取得了突破性进展[6]。目前,在信道译码方面的研究仍处于初步探索阶段[7]。文献[8]针对高密度奇偶校验码,采用卷积神经网络(convolution neural network,CNN)进行迭代译码,获得了优于BP译码算法的性能。为了降低训练的参数个数,文献[9]将译码参数与迭代次数相结合形成循环神经网络(recurrent neural network,RNN)进行迭代译码,用于有效解决中短码长线性分组码的译码问题。文献[10]分别利用多层感知机(multi-layer perceptron,MLP)、CNN以及RNN设计线性分组码译码器。结果表明,基于RNN的译码器性能最好,但计算时间最长,CNN译码器性能次之,MLP译码器性能最差。目前,尚未有深度学习技术应用于SC-LDPC码的译码。
为此,基于深度学习方法提出了一种SC-LDPC码的深度迭代译码算法,通过在消息传递边上引入权重系数并采用深度神经网络对权重系数进行训练来优化消息的可靠性度量值。
1 SC-LDPC码
SC-LDPC码通过将L个相同但互不相关的规则LDPC分组码通过空间耦合的方式连接成一条耦合链来构造,具体包括边展开和随机置换两个步骤。
步骤1边展开:考虑L个相同但互不相关的(dv,dc)规则LDPC分组码,其中dv、dc分别为变量节点和校验节点的度分布,每一个LDPC码对应于SC-LDPC码耦合链上的一个位置,记为u(u=1,2,…,L)。考虑满连接的边展开方式,设a为dv和dc的最大公约数,且a>1。那么一定存在一组正整数d′v和d′c满足dv=ad′v和dc=ad′c,且最大公约数gcd(d′v,d′c)=1,即每个位置上有d′c个变量节点和d′v个校验节点。位置u上的每一个变量节点有且仅通过一条边连接到位置u+i(i=0,1,…,a-1)上的一个校验节点。耦合链的末端需要添加a-1个校验节点以确保所有变量节点的边均能够连接到校验节点上。定义耦合宽度w=a-1。每个位置均进行上述边展开操作,就形成了一条(dv,dc,L)耦合链,其中L为耦合长度。
步骤2随机置换:由(dv,dc,L)耦合链构造一个SC-LDPC码,只需要对(dv,dc,L)耦合链进行一个“M-lifting”操作[11],其中M为随机置换矩阵大小。具体来说,将(dv,dc,L)耦合链看作一个原模图,然后进行“复制-置换”操作,即先将耦合链复制M次,然后再对M个耦合链中的边进行随机置换,得到一个(dv,dc,L,M)SC-LDPC码。
(dv,dc,L)SC-LDPC码集的基矩阵为
(1)
式(1)中:Bi(i=0,1,…,w)为分量基矩阵,大小为d′v×d′c,表示位置u上的d′c个变量节点和位置u+i上d′v个校验节点之间的边连接关系。
通过耦合,将每个位置上的每个变量节点dv条边分别连接到w+1个相邻位置的校验节点上,即将LDPC码原模图的基矩阵B拆分成w+1个分量基矩阵。分量基矩阵Bi(i=0,1,…,w)需满足式(2),且Bi中元素均为非负整数。
(2)
(dv,dc,L)SC-LDPC码集的设计码率为
(3)
以(3,6,L)SC-LDPC码耦合链为例描述其构造过程。图1(a)为(3,6)规则LDPC码原模图,基矩阵B=[3 3]。图1(b)为L个相同但互不相关的LDPC码原模图。然后,将L个互不相关的LDPC码原模图按照边展开规则连接得到一条SC-LDPC码耦合链,如图2所示。每一个LDPC码原模图对应耦合链上一个耦合位置,位置依次标记为1,2,…,L,耦合宽度w=a-1=2,a=gcd(3,6)=3,耦合链的末端添加了2个校验节点,分别标记为位置L+1和位置L+2。耦合链上的变量节点度是规则的,每一个变量节点连接3个校验节点;校验节点度是轻微非规则的,耦合链中间位置(位置3~L)上的每一个校验节点连接6个变量节点,耦合链两端的位置2和位置L+1的2个校验节点各连接4个变量节点,位置1和位置L+2的2个校验节点各连接2个变量节点。
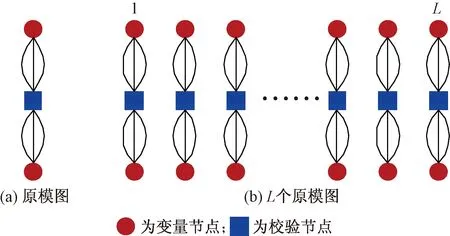
图1 (3,6)规则LDPC码原模图Fig.1 Potograph of (3,6) regular LDPC code
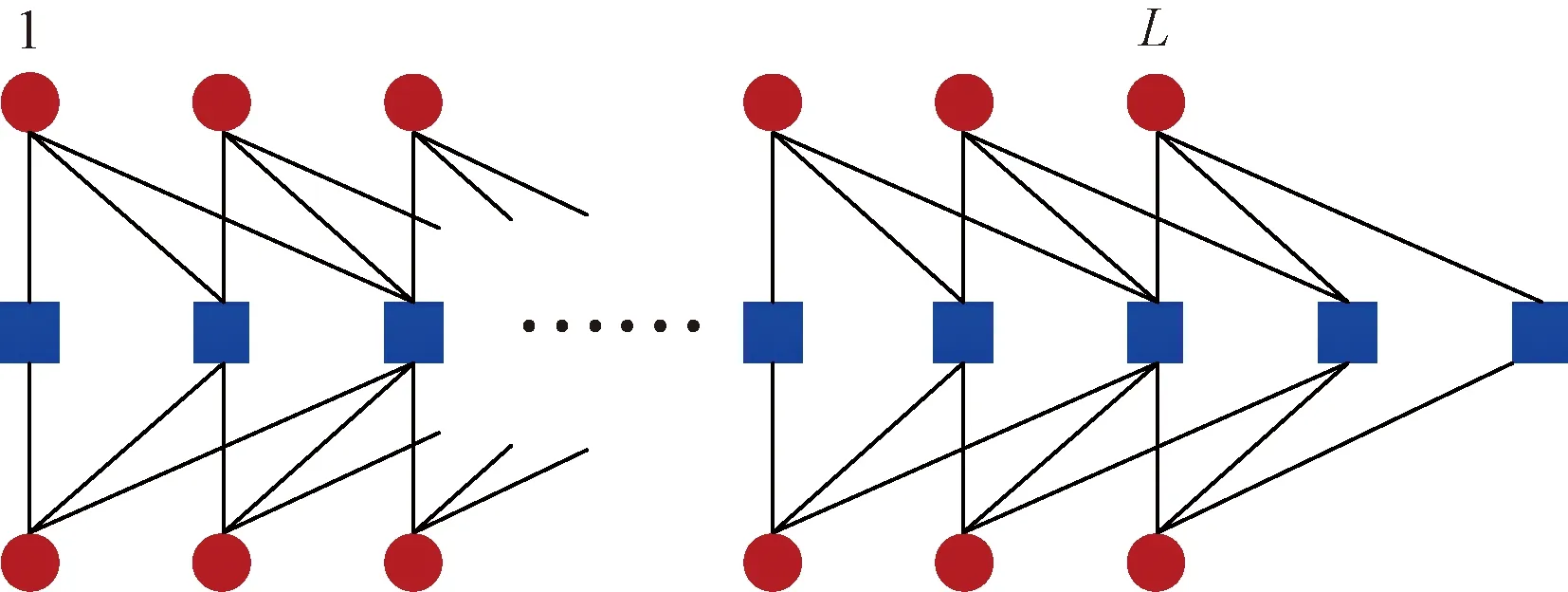
图2 (3,6,L) SC-LDPC码耦合链Fig.2 The coupled chain of (3,6,L) SC-LDPC code
根据式(2)可知,每个分量基矩阵为B0=[1 1]=B1=B2,则(3,6,L)SC-LDPC码集的基矩阵为
(4)
(3,6,L)SC-LDPC码的设计码率为
(5)
2 深度迭代译码算法
传统的BP迭代译码算法是在Tanner图边上迭代更新变量节点消息和校验节点消息。具体来说,每一个校验节点根据从与其相连的变量节点处接收到的消息计算输出给变量节点的消息。同样地,每一个变量节点进行类似的过程,根据从与其相连的校验节点处接收的消息计算输出给校验节点的消息。当达到最大迭代次数时,变量节点将接收的所有信息进行判决。由此可以看出,每个变量节点传递给相连的校验节点的消息均相等;反之亦然,每个校验节点传递给相连的每个变量节点的消息也相等,即Tanner图上每个节点相连的边上的消息的可靠性度量值相等,会带来错误消息的持续传播,降低译码收敛速度。
针对此问题,提出一种深度迭代译码算法,在消息传递及更新过程中引入权重系数,并采用深度神经网络对其训练获取该权重系数,以此来优化每次迭代过程中不同边上消息的可靠性度量值,从而减少SC-LDPC码在传统迭代译码算法下的迭代次数,加快收敛速度。具体来说,将迭代译码中Tanner图的边信息作为全连接深度神经网络(deep neural network, DNN)的输入,经过多层DNN处理Tanner图边上的消息,降低边上错误消息的权重,增大正确消息的权重,以此来优化消息传递过程中边上消息的可靠性度量值。

图3 含4层隐藏层的深度神经网络架构Fig.3 DNN architecture with 4 hidden layers
设定最大迭代次数为Lmax,SC-LDPC码长为N,N=d′cLM,Tanner图中总边数为E,E=dv×N。神经网络包含一层输入层,2Lmax层隐藏层,一层输出层。输入层是一个N长的矢量,由接收码字的对数似然比(log likelihood ratio, LLR)信息构成。所有隐藏层的神经元数量均为E,每一个神经元对应于Tanner图中的一条边上的信息。对于奇数层,每一个神经元的信息对应于Tanner中变量节点传递给校验节点的消息;对于偶数层,每一个神经元的信息对应于Tanner中校验节点传递给变量节点的消息。神经网络会给Tanner图中的每一条边分配权重系数,并对其进行训练。输出层是长度为N的译码码字。深度神经网络结构如图3所示。深度迭代译码算法具体步骤如下。
步骤1初始化。计算接收码字初始LLR值lv,其计算公式为
(6)
式(6)中:yv为对应第v个码比特Cv的信道输出,v=1,2,…,N;Pr(Cv=1|yv)为接收到yv后变量节点为Cv=1的概率;Pr(Cv=0|yv)为接收到yv后变量节点为Cv=0的概率。
步骤2变量节点消息更新,可表示为
(7)
式(7)中:i=1,2,…,2Lmax,式(7)仅对奇数i更新;e=(v,c)为Tanner图中连接第v个变量节点和第c个校验节点的边;wi,v为初始LLR值lv的权重;e′=(v,c′)为Tanner图中连接第v个变量节点和第c′个校验节点的边,其中c′不包含第c个校验节点;xi-1,e′为e′边对应的LLR;wi,e,e′为对数似然比xi-1,e′的权重;对于所有的e′,初始化x0,e′=0。
步骤3校验节点消息更新。
(8)
式(8)中:e′=(v′,c)为Tanner图中连接第v′个变量节点和第c个校验节点的边,其中v′不包含第v个变量节点,式(8)仅对偶数i更新。
步骤4判决输出。
(9)
式(9)中:w2Lmax+1,v为初始LLR值lv的最终权重;x2Lmax,e′为e′边对应的LLR;w2Lmax+1,v,e′为对数似然比x2Lmax,e′的最终权重;σ(x)=max(0,x)为激活函数。
利用交叉熵函数作为损失函数进行训练。
(10)
式(10)中:L(o,y)为信道输出y与神经网络输出o的损失;ov为神经网络的输出;yv为传输码字的第v个比特。
3 仿真结果
为了验证深度迭代译码算法的译码性能,构造多组不同参数的SC-LDPC码的校验矩阵。发送端依次使用不同码率的SC-LDPC码进行编码,采用BPSK调制,传输信道选取加性高斯白噪声(additive white Gaussian noise, AWGN)信道,接收端分别采用深度迭代译码算法,传统迭代译码算法以及滑窗译码算法进行译码恢复信息。
搭建的仿真实验环境为Tensorflow1.15,采用Python脚本语言,GPU使用NVIDIA的RTX3070显卡。训练数据集由经过AWGN信道传输后的接收序列生成,信噪比变化范围为0~6 dB,训练数据集的Batchsize大小为5 000,Minibatch大小为100,其中每个信噪比包含200组数据,测试数据集的生成与训练数据类似。DNN训练所采用的参数配置如表1所示。

表1 参数配置Table 1 Parameter configurations
首先,构造两组不同度分布的SC-LDPC码,分别为(3,6,15,32)SC-LDPC码与(4,8,15,32)SC-LDPC码。(3,6,15,32) SC-LDPC码耦合链长度15,随机置换矩阵大小为32,耦合宽度w=2,分量基矩阵为B0=B1=B2=[1 1],设计码率为0.433 3。 (4,8,15,32)SC-LDPC码耦合链长度15,随机置换矩阵大小为32,耦合宽度w=3,分量基矩阵为B0=B1=B2=B3=[1 1],设计码率为0.4。仿真结果如图4所示,窗口尺寸分别为3和4。结果表明,当迭代次数均为5时,深度迭代译码算法的译码性能优于传统迭代译码算法和滑窗译码算法的译码性能。
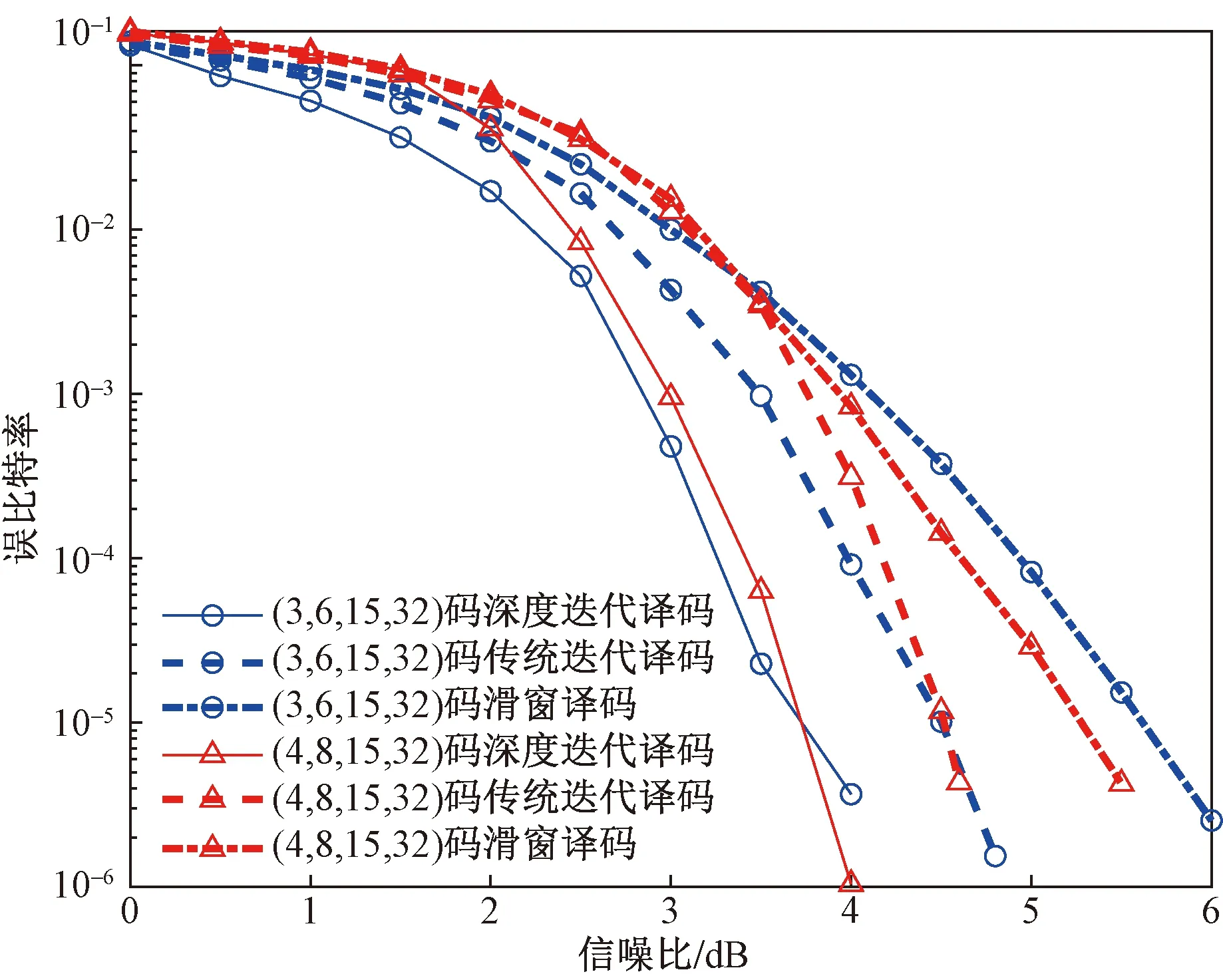
实线为深度迭代译码算法;虚线为传统迭代译码算法;点线为滑窗译码算法图4 度分布不同时,SC-LDPC码的译码性能对比Fig.4 Performance comparisons of SC-LDPC codes with different degree distributions
其次,构造三组不同耦合长度的(3,6,L,32)SC-LDPC码,耦合长度L依次取10,15,20,分量基矩阵均为B0=B1=B2=[1 1],设计码率依次为0.4,0.433 3和0.45。译码性能对比结果如图5所示,可以看出,在不同耦合长度下,当迭代次数均设置为5时,深度迭代译码算法的译码性能优于传统迭代译码算法和滑窗译码算法的译码性能,且随着L的增大,译码性能逐渐提升,与SC-LDPC码的自身特性相吻合。
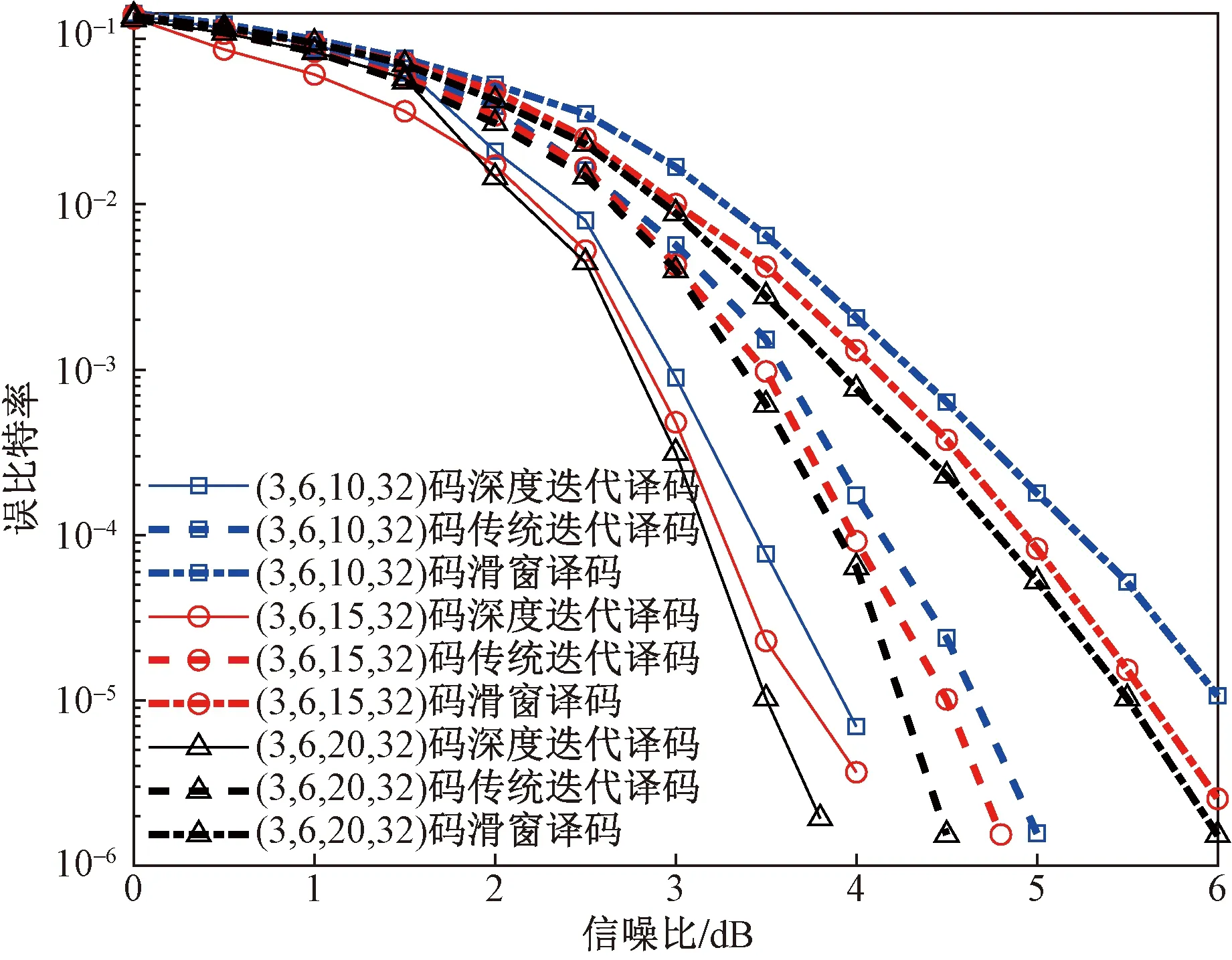
图5 耦合长度不同时,SC-LDPC码的译码性能对比Fig.5 Performance comparisons of SC-LDPC codes with different coupling lengths
最后,构造两组随机置换矩阵大小不同的(3,6,15,M)SC-LDPC码,随机置换矩阵大小M分别取32和64,分量基矩阵均为B0=B1=B2=[1 1],设计码率均为0.433 3。误码性能对比结果如图6所示,可以看出,在不同的M下,当迭代次数均设置为5时,深度迭代译码算法的译码性能均优于传统迭代译码算法和滑窗译码算法,且M越大,译码性能越好,这与SC-LDPC码的特性保持一致。
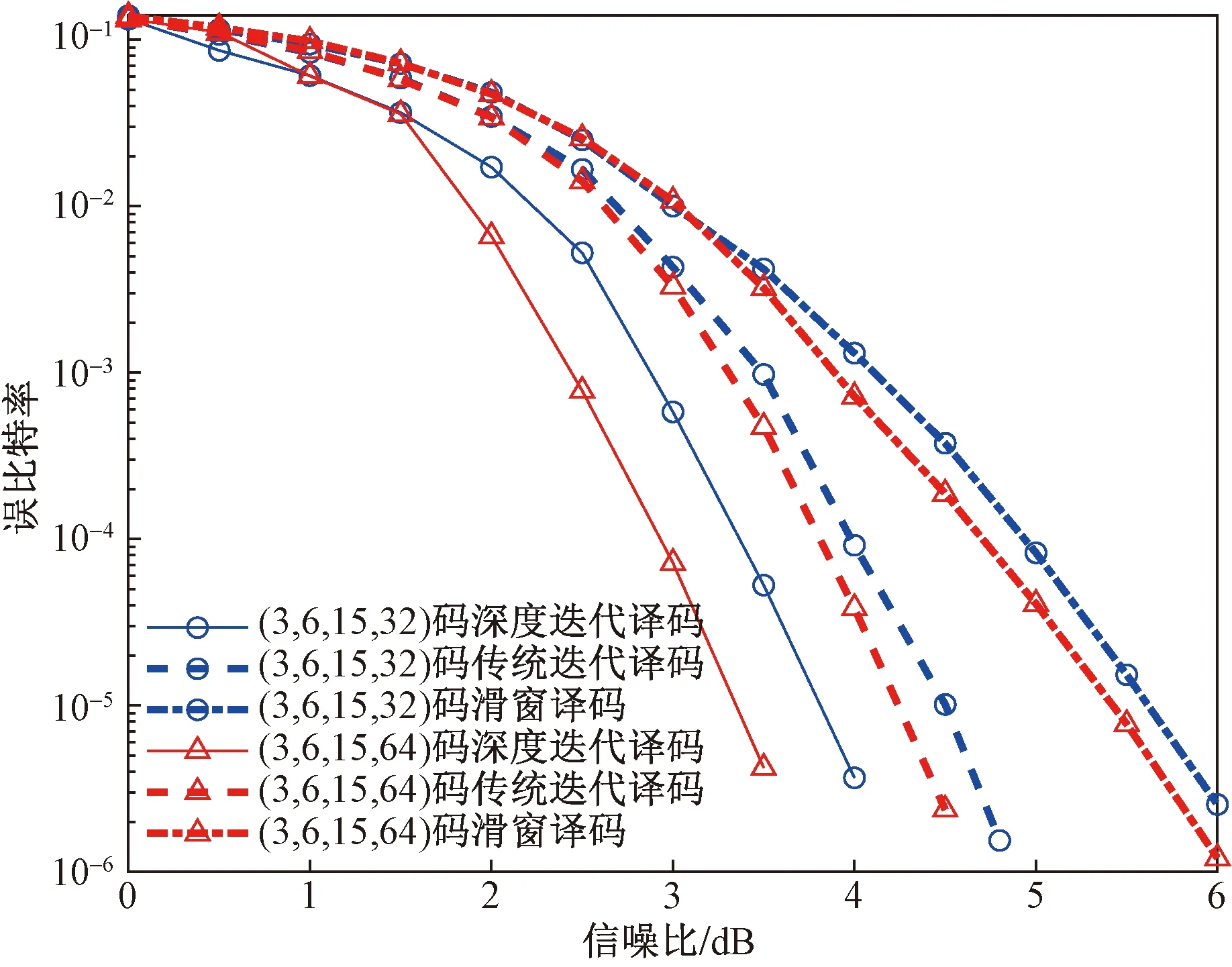
图6 置换矩阵大小不同时,SC-LDPC码的译码性能对比Fig.6 Performance comparisons of SC-LDPC codes with different random permutation matrix sizes
4 结论
提出了一种SC-LDPC码的深度迭代译码算法,得出如下结论。
(1)该算法在消息传递过程中引入权重系数,并采用深度神经网络对其训练获取该系数,可以优化边上消息的可靠性度量值,加快译码收敛速度,提升译码性能。
(2)仿真结果表明,在相同迭代次数下,对于不同度分布,不同耦合长度,不同随机置换矩阵大小的SC-LDPC码,所提出的深度迭代译码算法的译码性能均优于传统迭代译码算法和滑窗译码算法的译码性能,同时还保留了SC-LDPC码本身的特性。
(3)将深度学习技术与传统无线技术相结合,可以有效提升传统算法的性能,智能通信有望成为未来通信发展的主流方向之一。
