覆冰八分裂导线舞动过程中的次档距振动研究

刘宇， 蔡萌琦， 王清远，3*， 黄春林， 丁顺利， 周林抒

(1.成都大学机械工程学院， 成都 610106； 2.成都大学建筑与土木工程学院， 成都 610106；3.四川大学破坏力学与工程防灾减灾四川省重点实验室， 成都 610065； 4.国网四川综合能源服务有限公司， 成都 610031)

现阶段中国存在电力供需关系不平衡的问题，因此根据电力的供需关系，常需要面临超长距离的、跨区域的输电。自然特高压输电线路的安全运行会受到工作环境的影响。由于外部环境的突变性和复杂性，线路正常运行面临着严峻的挑战。调查研究发现，非对称横截面积冰导体的气动不稳定性引起覆冰导线舞动，该现象是自激的流固耦合振动，也许会导致其输电线路的断裂和短路，更甚者，还会造成输电塔的崩塌[1]。因此，对于输电线路的防振是当下电气工程和材料工程领域的重点研究方向。

严波等[2]用Hamilton变分原理建立系统的动力学平衡方程，对比子导线在迎风侧和背风侧的空气动力载荷，探索其载荷数据不同是否是由其导线的尾流造成的，从而为分裂导线舞动的深入研究提供了一种有效的途径。蔡萌琦等[3]对扇形覆冰八分裂导线进行了风洞节段模型试验，并采用数值方法分析了覆冰八分裂导线在不同参数下的舞动特性。向玲等[4]将模拟所得各子导线气动力系数换算为整体气动力系数加载到超高压输电线路的有限元模型，模拟线路的整体舞动。黄军凯等[5]总结了容易产生舞动的气象特点和输电线路结构设计参数对舞动发生的影响。现如今，特高压输电线路使用八分裂的结构架式，在风速和覆冰的情况下会造成线路的舞动。若线路设计不合理，则导线间隔棒的动弯曲应变会随着子导线振动频率的增加而增加，从而导致导线和间隔棒的损伤，进而造成线路断裂或短路，对电网的正常运行造成严重威胁。基于此，通过采用数值模拟的方法对覆冰八分裂导线的舞动过程进行模拟，旨在研究覆冰八分裂导线舞动过程中的次档距振动现象和特征。

1 典型线路段及有限元模型

以覆冰特高压输电线路为研究对象，选取200、400 m的档距进行深入分析，该输电线路采用8×LGJ-500/35的型号，12 mm的典型覆冰厚度，30 mm的计算截面直径，其余参数如表1所示，200、400 m线路的模型图如图1所示。

覆冰特高压输电线路的气动参数利用风洞实验的结果进行分析[6-8]，整体采用有限元数值法计算，在导线上施加了气动力，从而对导线的舞动数值模拟。计算时，利用ABAQUS，在刚度和无质量的用户自定义单元，索单元的节点在施加了空气动力的情况下，可以得到其扭转角、速度和位移。安装4个间隔棒在200 m的输电线路上，第一个间隔棒距离左端31 m，其余依次增加50、47、46、26 m。400 m输电线路上安装7个间隔棒，第一个间隔棒距离左端40 m，其余依次增加50、55、55、55、55、50、40 m。

假设该段导线两端为耐张塔，在分析的过程中将线路因为塔杆的影响忽略不计，间隔棒2采用的是FJZ- 450的型号，质量为17.5 kg，在每根导线的两端设置6个自由度的约束，进而建立数值模型。间隔棒与覆冰导线在利用梁单元及索单元进行离散计算发现，当长度是0.5 m的索单元时，会达到收敛。

数值模拟中，通常采用Rayleigh的阻尼模型，可表示为

表1 覆冰八分裂导线参数Table 1 Parameters of iced eight-bundle conductor

图1 八分裂线路模型Fig.1 The model of eight-bundle conductor line

C=αM+βK

(1)

式(1)中：α和β为Rayleigh阻尼系数；C为阻尼矩阵；M为质量矩阵；K为刚度矩阵。

2 整档模型及次档内局部模态

在特高压输电线路的安装设计过程中，考虑安装现场的气候特点和地形风貌，根据实际的计算反馈确定导线的张力和档距布局，不同的参数对输电线路的固定频率会产生一定程度的影响。当输电导线发生舞动时，线路在发生整档舞动外，时常伴随着子档距间的振动[9]。固有频率及模态影响着导线的整档舞动的方式。利用ABAQUS软件，将线路的参数代入其中，得到其固有频率和整档模态如表2所示。查表可知，输电线路在200 m档距的情况下，其面内单半波0.26 Hz的固有频率小于面内双半波0.52 Hz的固有频率，并且面内单半波的频率几乎是双半波固有频率的1/2。扭转三半波0.83 Hz的固有频率与面外三半波0.80 Hz的固有频率近乎相等。对于400 m档距的线路，其面内单半波0.14 Hz的固有频率小于面内双半波0.29 Hz的固有频率，并且面内单半波的频率接近是双半波固有频率的1/2。面外三半波0.43 Hz的固有频率与扭转三半波0.48 Hz的固有频率与几乎相等。不难发现在此情形中，存在1∶2和1∶1的内共振条件[10]。

线段的固有频率和典型的次档距模态如图2所示。可以看出，一个相对密集的固有频率集中在1.043～1.138 Hz的频率范围内，拥有面内、面外和扭转3种方向，单半波、双半波、三半波和四半波模态。

表2 覆冰八分裂导线整档模态及其固有频率Table 2 Modes and natural frequencies of iced eight-bundle conductor

f为固有频率图2 典型次档距局部模态(200 m档距)Fig.2 Typical subspan partial mode (200 m span)

3 导线舞动过程中的档内振动

3.1 特征段导线各次档距振动情况

利用数值模拟的方法对覆冰特高压输电线路在给定的风速下的舞动过程进行模拟分析[11-14]。风速为8 m/s的情况下200 m档距覆冰八分裂导线子导线1在各间隔棒中点的位移时程如图3所示[15-16]。观察对比，在8 m/s的风速下，因为其导线间的气动力不同，垂直方向的振动幅值相对于水平方向的振动幅值更明显，并且越靠近导线的中间位置，其振动越剧烈振动幅值越大。次档距1～5的水平振动幅值区别不大，但垂直振动幅值区别明显。考虑到尾流和气动载荷的影响，子导线次档距1和次档距5、次档距2和次档距4的幅值成基本上近似对称状态。其中，舞动开始一段时间之后，导线的舞动趋于稳定，其中水平舞动趋于稳定的速度比垂直舞动趋于稳定的速度更快。

图3 风速8 m/s时200 m档距覆冰八分裂导线子导线1的各间隔棒中点位移时程Fig.3 Displacement time history of the midpoints of the spacers of the sub-conductor 1 of the iced eight-bundle conductor at a wind speed of 8 m/s with a 200 m span

对比垂直位移反应谱分析部分(图4)，以图4(a)为例，次档距1中出现的首个突出的峰值频率是0.45 Hz，与面内双半波的0.52 Hz(表2)固有频率接近。次档距1中出现的第二个凸起的峰值频率为0.82 Hz，与面外三半波的0.80 Hz(表2)固有频率接近[17]。由此可知，分裂导线舞动过程中存在档内振荡。图4(c)频谱值较大，说明次档距3处振动明显。

3.2 不同风速下导线舞动及次档振动研究

不同风速下线路舞动过程各子导线振动幅值和垂直振动的幅值均有增加，其中垂直振动的振幅增加明显，达到11 m。

当风速为8 m/s时，各子导线之间垂直振动和水平振动的位移大致相同；在典型风速12 m/s时，因为尾流的干扰导致各子导线的气动载荷不同，覆冰八分裂各子导线振动的幅值明显不同，如表3所示，伴随着风速的增加，子导线水平振动幅值也相应地增加，但相对于垂直振动幅值，增加的速率较缓和。

表3 不同风速下线路舞动过程各子导线振动幅值Table 3 Galloping amplitude of each sub-conductor during line galloping under different wind speeds

3.3 不同档距下导线舞动及次档振动研究

为了研究不同档距振动特性，给出了200 m和400 m档距风速12 m/s情况下中点各子导线的位移情况如图5所示[18]。由图5(a)可以看出，200 m档距中点的垂直位移大于水平位移，且各子导线的垂直位移和水平位移大致相似，其轨迹近似为椭圆形。由图5(b)可以看出，在400 m档距中点的垂直位移和水平位移没有明显的区别，且各子导线的振动轨迹在相对于集中的空间里振动，由于每个子导线的舞动轨迹不同，说明存在着次档距内的振动。

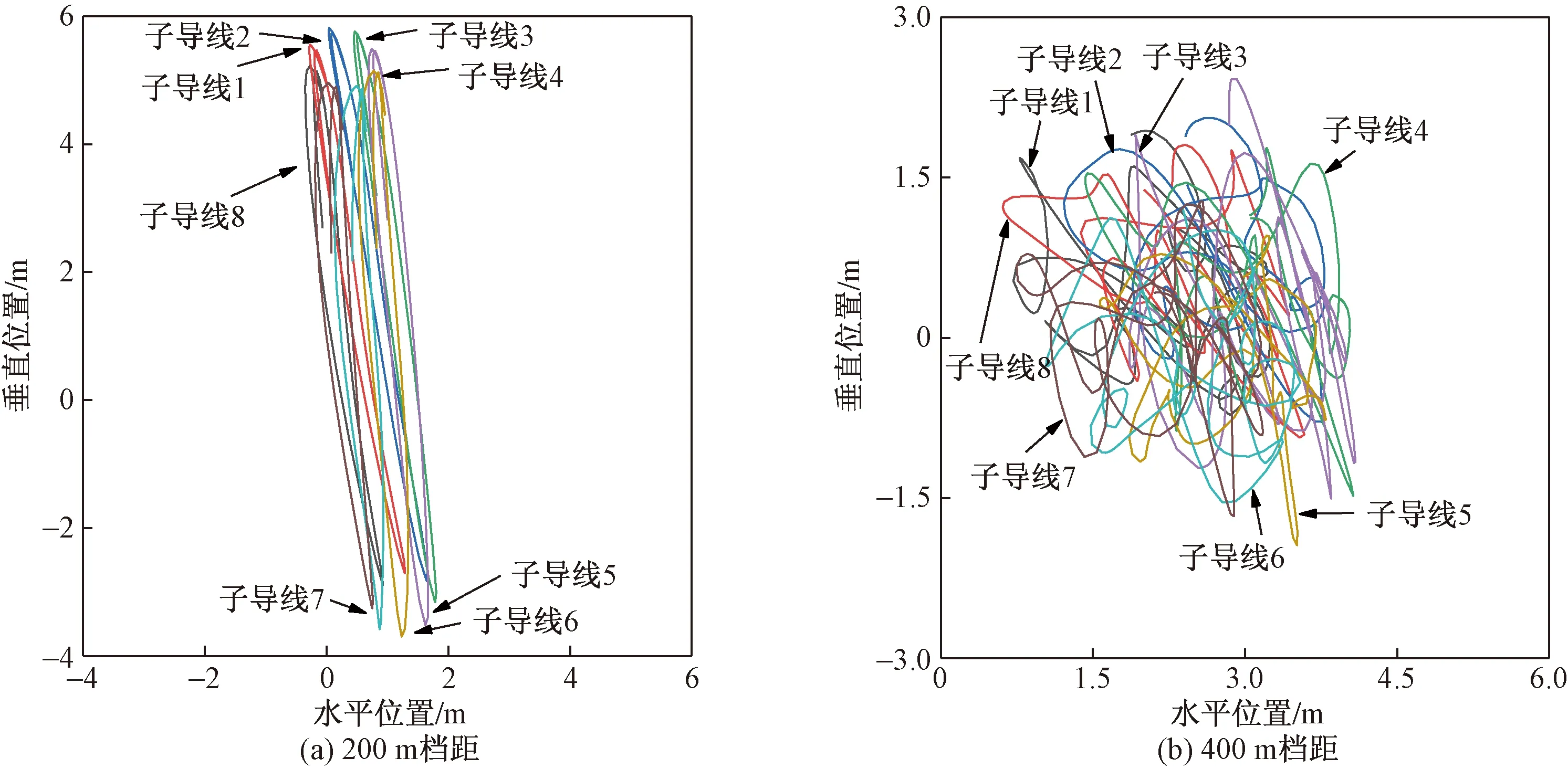
图5 200 m和400 m档距风速为12 m/s时中点各子导线的位移情况Fig.5 Displacement of the sub-conductors at the midpoint when the wind speed is 12 m/s at the 200 m and 400 m span-length

图6 风速12 m/s时中点处各自导线舞动间距随时间变化Fig.6 Variation of the galloping distance of the respective conductors at the midpoint with time when the wind speed is 12 m/s

3.4 次档距中的导线振动情况

次档距1中点处各子导线舞动间距随时间变化如图5所示。子导线5、子导线6、子导线7和子导线8在下风侧的竖向振动振幅大于子导线1、子导线2、子导线3和子导线4在上风侧的竖向振动振幅[19-20]。在200 m档距情况下，风速为12 m/s时，次档距3中点的各子导线间的舞动间距随着时间的变化情况如图6所示。通过表格我们可以发现，在400 s时，各子导线间的间隔达到最大，随后随着时间的推移，各子导线间的距离波动式的靠近；子导线1和2、子导线5和6的距离相对较远，而子导线6和7的距离相对较近。

4 结论

采用数值模拟分析的方法研究了覆冰特高压输电线路的舞动特性，观察研究了其线路在舞动过程中的档内振动，从而得到如下结论。

(1)覆冰八分裂输电线路各子导线在不同风速下舞动的方向均相同，且主要的振动方向为竖直方向。

(2)因为受到尾流干扰和气动载荷的影响，子导线在不同的风速下振动的幅值不相同，在导线的承载范围内，导线振动的幅值与风速的大小呈正相关。

(3)子导线的舞动时程图极限为一个斜椭圆形，超过极限则时程图变得不规则。

(4)由于尾流的干扰，在相同风速下，下风侧的子导线在竖直方向上的振动振幅高于上风侧。

(5)覆冰八分裂导线舞动过程中存在着档内振动，该振动可能会导致子导线间发生碰撞。研究结论对特高压输电线路的舞动原理的研究和防振具有一定意义的参考。