基于局中人平方超量的区间数均分剩余值及其在冷链物流联盟合作收益分配中的应用
2022-05-19罗妍程鹏斐范伯龙刘家财
罗妍, 程鹏斐, 范伯龙, 刘家财
(福建农林大学交通与土木工程学院, 福州 350002)
由于受外部环境、市场变化等不确定因素的影响,决策环境具有复杂性、信息不完全性,同时,受人类思维不确定性影响,局中人的联盟值通常使用模糊数而非精确值表示[1-3]。区间数合作博弈即以区间数表示联盟特征(支付)函数的合作博弈,是联盟值具有不确定性的合作博弈的一种重要形式。在区间数合作博弈中,联盟值无法用精确值表示,只能估计出联盟值的闭区间取值范围。作为经典(清晰)合作博弈的推广,多数学者近年来都对模糊合作博弈开展研究[4-10]。李登峰等[4]利用区间数距离概念和最小平方法,建立以联盟分配与联盟支付值之差的平方和为最小的数学优化模型,据此确定每个局中人的区间数分配;杨靛青等[5]针对模糊合作博弈中局中人可能形成多层级联盟结构的情况,利用Choquet积分定义多层级模糊联盟结构,提出了斑兹哈夫值解概念及其解法;肖燕等[6]利用梯形模糊数距离(平方)概念和最小平方法,建立最小化局中人联盟分配和支付值差值平方和的优化模型,根据模型推导出联盟成员梯形模糊数分配值的解析公式,探讨该最小平方解的重要性质。Zhao等[7]提出了一种联盟值用三角模糊数表示的合作博弈解,据此获得用三角模糊数表示的局中人收益值。刘悦等[8]针对对象评价值是区间数的多属性决策问题,通过分析区间数之间的模糊优势关系,提出一种新的决策方法;苏世彬[9]提出了三角模糊数型多人收益分配合作博弈及区间数核心解概念和基于满意度的三角模糊数型多人收益分配合作博弈求解方法;韩二东等[10]针对主客观混合评价信息的供应商选择决策问题,提出一种基于直觉模糊交叉熵及灰色关联的群决策方法。杨洁等[11]通过引入α-矩阵博弈的概念,提出一种求解支付值为梯形模糊数的矩阵博弈线性规划方法;在区间数合作博弈中,崔春生等[12]针对联盟值部分未知的区间合作博弈,定义了残缺区间合作博弈的相关概念,基于合作博弈的超可加性,建立了联盟区间收益值的一致性验证模型;南江霞等[13]从个人超出值的视角研究了特征函数为区间数的合作博弈和联盟为模糊集的无限模糊联盟区间数合作博弈。
企业联盟的合作收益分配策略问题是一种典型的合作博弈问题,理论上,现有经典合作博弈的单值解均可以应用于解决企业联盟的合作收益分配策略问题。然而,一些著名的合作博弈单值解,由于受子联盟无法成立、联盟值无法预测等客观因素的影响,在实际情况中并不适用,如Shapley值和Banzhaf值。使用Shapley值解决合作收益分配策略问题时,每个子联盟都应能够形成且其联盟值必须能够事先预知,然而这在实际情况中是很难实现的。以冷链物流合作联盟为例,目前市面上常见的中小型冷链物流企业车辆保有种类单一,冷藏或冷冻温度覆盖范围小,而对于冷链物流行业而言,单一的车辆种类与温区范围很难适应市场的需求。因此,对于拥有相同或相近种类冷藏车的企业来说,很难开展合作,从而联盟值无法预知。近年来,学者们对部分经典的合作博弈单值解进行改进,提出了一些改进的合作博弈单值解,如改进的Shapley值和改进的Banzhaf值[14-16],并将其应用于解决各个领域的合作收益分配策略问题[8,16-20]。魏针等[19]提出省属高校高考招生计划分配的破产模型及Shapley值分配算法,实现招生计划分配的有效性和合理性;祝新等[20]基于传统的医药冷链物流配送模型,在考虑道路通行状况对模型求解最优路径影响的基础上,建立了以综合成本为目标函数的配送模型。然而,这些合作博弈解大多延续了单值解需要满足个体合理性、超可加性、均衡性等假设的特点,且由于未考虑局中人参与的合作联盟的真实情境,所得结果并不满足公平性、合理性,无法应用于实际案例。
为此,基于冷链物流企业联盟的真实情境,考虑其中存在的模糊不确定性,利用区间数表示局中人参与的合作联盟的收益值,提出基于局中人平方超量的区间数均分剩余值及加权区间数均分剩余值,据此获得加入联盟的各个冷链物流企业的合作收益。
1 相关概念
1.1 区间数的运算
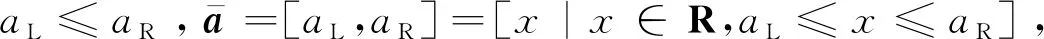
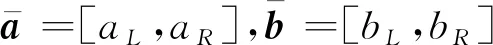
加法运算为
(1)
减法运算为
(2)
乘法运算为
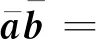
(3)
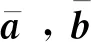
数乘运算为
(4)
式(4)中:λ为常数。
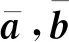
(5)
1.2 区间数合作博弈
联盟值用区间数来表示的合作博弈称为区间数合作博弈。设集合N={1,2,…,n},对任意子集S⊆N,函数v(S)满足:v(φ)=0,当S1⊂N,S2⊂N,v(S1∪S2)≥v(S1)+v(S2),即满足超可加性,则有序对(N,v)表示n人区间数合作博弈,v(S)为n人合作博弈的特征函数,表示联盟S的效益。有n个局中人的集合N={1,2,…,n}的所有联盟结构共有2n-1个(不计空集)。
在区间数合作博弈中,联盟值用区间数v(S)=[vL(S),vR(S)]表示,其中vL(S)≤vR(S)。
1.3 区间数合作博弈的局中人平方超量
受Liu等[21]提出的局中人剩余向量概念的启发,提出了区间数合作博弈的局中人平方超量的概念。局中人的区间数支付向量可表示为
x=[x(1),x(2),…,x(n)]T
={[xL(1),xR(1)],[xL(2),xR(2)],…,[xL(n),xR(n)]}T
(6)
e(i,x)=[vL(i)-xL(i)]2+[vR(i)-xR(i)]2
(7)
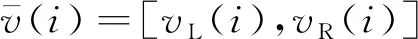
2 区间数均分剩余值解概念及解法
将最小平方法的思想应用于区间数合作博弈中,区间数距离(平方)公式为
(8)
2.1 未考虑权重影响的区间数均分剩余值
受区间数距离(平方)公式的启发,为求得最优支付向量,建立下述二次规划模型。
问题1
(9)
满足约束条件:
(10)
问题1的拉格朗日方程L(xE,λE,μE)可表示为
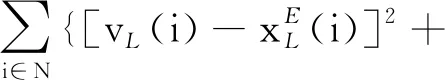
(11)
式(11)中:xE为所求收益分配向量;λE及μE为拉格朗日乘数法中的参数。
令向量
xE*=[xE*(1),xE*(2),…,xE*(n)]T
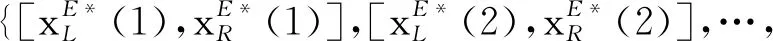
(12)
式(12)表示问题1的最优解,对L(xE,λE,μE)关于变量xE、λE、μE分别求偏导并令其等于0,则有
(13)
解得
(14)
根据式(14)可得
(15)
式(15)中:n为大联盟中局中人个数。
因此,有
(16)
由式(15)、式(16)可得
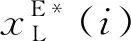
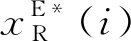
(17)
整理得

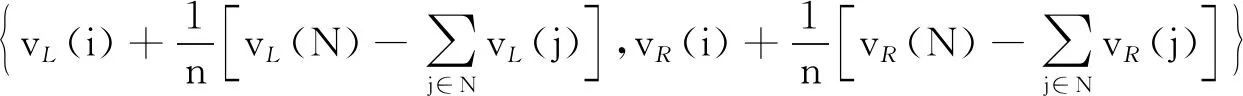
(18)
式(18)即为区间数均分剩余值的解析式。
2.2 加权区间数均分剩余值
在实际情况中,不同局中人对联盟的投入、所承担的风险等因素是不相同的。因此,合作收益分配问题中考虑局中人重要性的影响是十分必要的。在冷链物流领域,中、小型物流企业所保有车辆类型有所不同,中型冷链物流企业大多保有车厢内部平均温度小≤-20 ℃的F类冷藏车,而运输蔬果类小型物流企业保有车辆类型大多为车厢内部平均温度在12~-10 ℃的B类冷藏车,显然,当合作联盟达成后,运输冷冻食品和生鲜蔬果类货物时,不同企业所承担的运输量以及对合作联盟的贡献等都是不同的,因此,若不考虑权重的影响,则合作收益分配策略显得有失公平。为解决上述问题,提出了考虑权重影响的区间数均分剩余值。
问题2
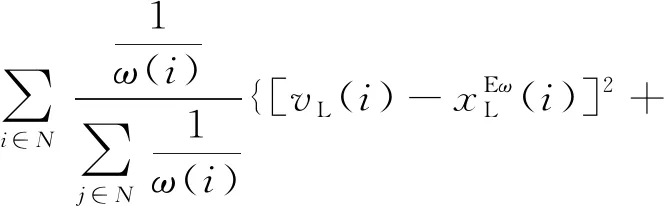
(19)
满足约束条件:
(20)
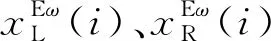
问题3

(21)
满足约束条件:
(22)
式(21)的拉格朗日方程可表示为
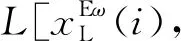
(23)
式(23)中:λEω及μEω为拉格朗日乘数法中的参数。
令向量
xEω*=[xEω*(1),xEω*(2),…,xEω*(n)]T
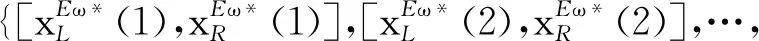
(24)
表示问题3的最优解,与问题1求解方法类似,可得
(25)
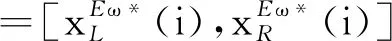
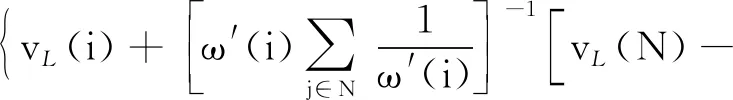
(26)
式(26)即为加权区间数均分剩余值的解析式。与区间数均分剩余值显著不同的是,加权区间数均分剩余值并非简单地将合作后取得的剩余收益等分,而是综合考虑了局中人对联盟的投入、所承担的风险等影响因素对合作收益分配策略的影响。
2.3 区间数均分剩余值的性质
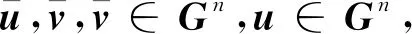
(27)
证明:由式(19)可得

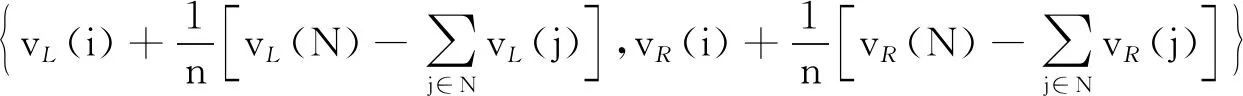
(28)
则有
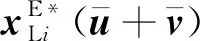
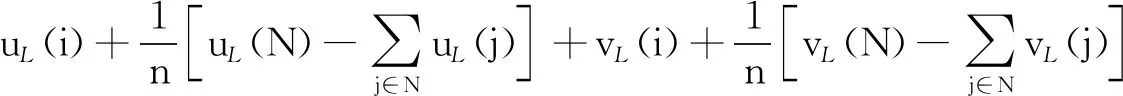
(29)
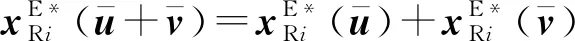
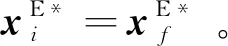
证明:根据式(18)得
(30)
局中人i和局中人f(i≠f),有
(31)
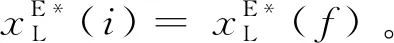
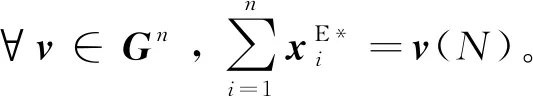
证明:
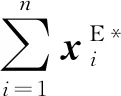
=v(N)
(32)

3 实例计算分析
假设有3家不同的冷链物流企业(即局中人)均要为某地配送生鲜农产品,决定冷链物流企业收益的诸多影响因素,如油价、人工成本、交通环境、天气气候、城市道路状况等,均具有一定的模糊不确定性,很难用精确值进行量化,只能给出其大致范围,用区间数表示相应影响因素的取值范围则可以很好地解决这一问题。核算冷链物流企业成本时需要用到的参数如表1所示,具体数值可根据不同企业自身情况测算。
根据表1所示数据,冷链物流企业运输收益值可表示为
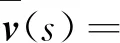
(33)
此例中,提出假设:①冷链物流企业在采购运输车辆时,考虑到运输产品类型及成本等原因,不会同时采购市面上所有型号的车辆,因此,假设冷链物流企业仅拥有有限车型;②在冷链物流企业联盟成立后,企业之间共享车辆类型及运输信息,因此假设本例中运输车辆均满载。
如图1所示,3家冷链物流企业(即局中人)分别用企业1、企业2、企业3表示,企业1和企业2为小型冷链物流运输企业,运输产品包括大量蔬菜、水果等需要冷藏保存的蔬果类食品,少量鱼、肉、海鲜等需要冷冻保存的生鲜类食品,由于其保有车辆种类仅为车厢内部平均温度在12~-10 ℃的B类冷藏车,因此,当运输需冷冻保存的产品时需要临时租赁温度符合要求的F型车辆;企业3为中型冷链物流运输企业,为商超便利企业运输产品,保有车辆种类为车厢内部平均温度不高于-20 ℃的F类冷藏车,但由于其参与联盟前仅为商超便利提供服务,车辆未满载就发车的情况时常出现,造成资源浪费。联盟成立后,3家冷链物流企业共享保有车辆及运输信息,互补了各自车辆种类不全、满载率不高等问题。

表1 冷链物流企业成本核算相关参数Table 1 The relevant parameters of cold chain logistics enterprise cost accounting
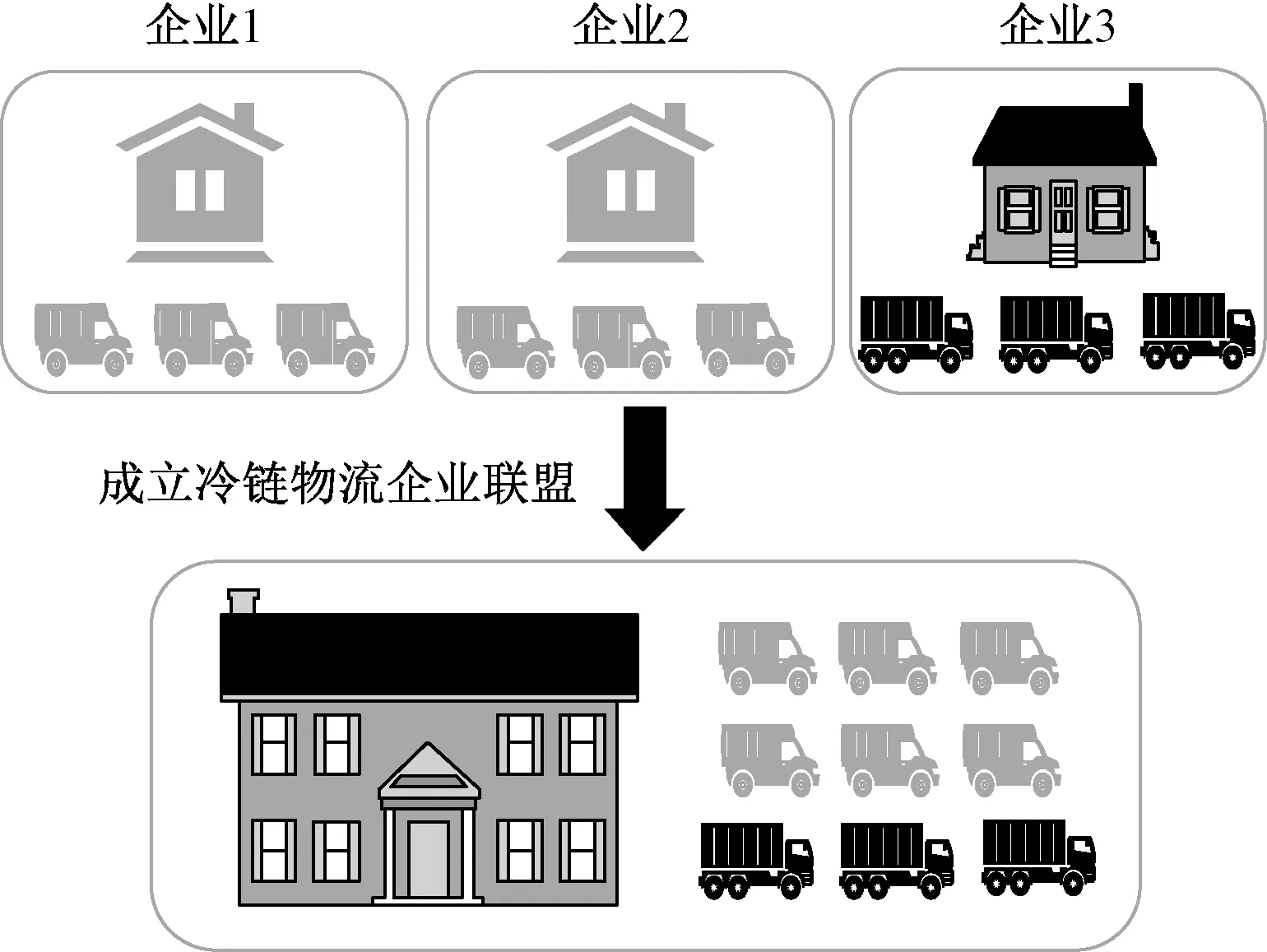
图1 合作联盟成立示意图Fig.1 Schematic diagram of the establishment of the cooperative alliance
考虑到3家物流企业的企业规模、市场占有率、市场信誉及车辆保有情况,经专家评判,三家企业在分配合作收益时的权重分别为0.2、0.3和0.5。其单干、合作子联盟与大联盟的收益情况计算参数及结果如表2所示。

表2 子联盟收益计算参数Table 2 Sub-alliance income calculation parameters
由表2可知,企业1与企业2在企业规模大小、车辆保有类型等方面均相似,因此二者联盟后,联盟规模扩大,所承接业务量及业务种类增多,但二者车辆类型一致,在运输运单量大的订单时,只能由多辆载运量小的冷藏车进行配送。同时,由于冷藏车温度不达标,极易造成冷冻食物在运输过程中腐坏的现象,因此,当企业1与企业2联盟时,会造成资源浪费与货物腐败,联盟反而提高运输成本,联盟无法成立。企业1与企业3、企业2与企业3联盟成立后,车辆类型更加丰富,满足运输需求,同时由于企业规模增大,信息共享,运输成本降低,订单量增多,运输成本降低,收益值增加,联盟可成立。
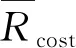
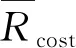
=[RL,RR]
=[647.25,1 000.76]
(34)
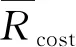
(35)
其余联盟的收益值算法类似,此处不做赘述。最终所得联盟值如表3所示。

表3 子联盟收益值汇总Table 3 Summary of income value of sub-union
显然,由表3可知,联盟{1,2}由于其车辆保有种类与企业规模大小均相似,合作后所获剩余向量不达预期,联盟不具有稳定性,在实际情况中,二者联盟很难成立,合作收益值很难预估。此例中,子联盟{1,2}不满足超可加性,无法获得子联盟的收益值,因此无法使用Shapely值和Banzhaf值进行分配策略的求解。所提出的两种方法,由于无需预知所有子联盟的收益值,完美避开传统合作博弈求解方法的局限性,可轻松解决此类问题。不同解决方案的计算结果如表4所示。

表4 不同情况的收益分配结果Table 4 Income distribution results in different situations
由表4可以看出,企业1、企业2、企业3在加入合作联盟后,所得收益较单干时收益更多,满足个体合理性,且其联盟成立后所得收益值之和大于3家企业单干时所得收益,大联盟满足超可加性。此外,由于3家冷链运输企业达成合作后,其车辆类型及运输信息共享,解决了中小型物流企业车货不匹配、运输资源浪费的问题,同时合作收益分配策略公平合理,因此合作联盟呈稳定状态。
加权区间数均分剩余值较区间数均分剩余值而言,考虑了企业规模、市场占有率、市场信誉及车辆保有情况等因素,增加了权重因子ω,因此,在冷链物流合作联盟企业利益分配的实际应用中更加公平合理。
4 结论
提出了两种基于局中人剩余向量利润分配策略的决策方案,较传统可转移效用博弈的解决方案而言,解决了由于子联盟不满足超可加性或无法成立时,无法采用传统合作博弈解计算分配策略的问题。同时,针对受环境、交通条件、气候影响等客观原因造成的局中人联盟值无法精确计算的问题,提出了使用区间数表示联盟值的方法。本文方法将合作联盟剩余向量考虑在内,所得的利润分配策略更加公平合理。所得解皆满足存在性、唯一性、有效性、个体合理性、超可加性、对称性、未知性等特性。在未来的研究中,将所提出的两种解法推广到其他模糊情境。
