基于多孔介质的某大口径装药床点传火特性

廖万予，薛晓春

（南京理工大学 能源与动力工程学院，江苏 南京 210094）

1 引言

主装药的点传火是影响火炮发射成功的关键因素。点火结构分为底部点火结构和中心传火管点传火结构。目前，在大口径火炮中，由于装填密度大，孔隙率低，因此广泛采用了中心传火管为主要结构的点传火系统，且大多采用管状药束。该点火过程由底火击发开始，而后逐步点燃管状药条。药条被点燃后产生高温高压的气体，经中心传火管壁的多个传火孔喷出，进入主装药室后点燃主装药；主装药燃烧后再次产生高压气体，顺利推动弹丸发射。由此可知，主装药能否被顺利引燃是点传火成功的关键。点火燃气进入药室后形成的温度场和压力场，都将影响到主装药的引燃：若温度场传播速度过慢，将影响药室内点火的均匀性和瞬时性；若压力场传播不均或压力波过大，会导致装药引燃失败，甚至发生发射安全性事故。然而，药室内温度场和压力场的形成，又与燃气在药室中流动时，受到的阻力相关。因此，研究主装药在药室中的分布特性对点火药燃气在药室中传播特性的影响尤其重要。

对于点传火过程，刘子豪等［1］建立了底火射流的一维两相流模型，对底火两相射流在传火管内的传播过程进行研究，得到传火管内传火变化规律，但没有将点火系统和特定药床结合进行分析。张艳明等［2］利用数值模拟研究了粒状发射药床点火燃烧的应力情况，模型中考虑到了中心传火管的点火系统。过去的点火过程研究一般只针对药室内发射药的燃烧，大多数将点火系统做了简单的替换；或是对传火管内点火药的传播规律研究较多，但对于将其与点火药燃气在药室中的传播过程结合的研究较少。高阳［3］以Fluent 软件为平台，模拟对象为球、柱型颗粒填充而成的圆管型多孔介质燃烧室，将软件自带的模型修改为适用于多孔介质的N-K 模型，并在冷流状态下对模型进行了验证；刘桂兵等［4］对多孔含能颗粒填充的非稳态传热过程进行了研究，模拟了填充药床内的温度变化特性，并总结了不同孔隙率影响下填充床的温度变化规律；Kamyar等［5］同样利用多孔介质模型模拟填充床内颗粒物的湍流运动，及不同颗粒物模型对湍流强度的影响特性，证明了将多孔介质模型作为填充床设计工具的可行性。药室内温度场和压力场的传播是否良好将决定主装药能否顺利点燃，装药的装填密度或初始孔隙率对温度传播特性和压力传播特性有极大影响，用合理的方法处理装填密度或初始孔隙率不同的装药颗粒在药室内的阻力分布特性十分重要，而利用多孔介质模型能够很好地模拟点火燃气在主装药床内的传播过程，再结合传火管内传火变化规律，即可完整地模拟密实装药床点传火过程。

本研究以某105 mm 大口径火炮密实装药床为背景，基于可燃中心点传火管的点传火方式，建立多孔介质模型并采用Fluent 软件模拟了高温高压的点火药燃气在主装药床内的传播过程，获得了药室内温度、压力演化特性及等温面传播速度，并通过与前期设计的点传火模拟试验平台的测试数据进行了对比，验证了仿真模型的可靠性；在此基础上，进一步研究了不同的主装药装填密度对药室内特性参数的影响规律。

2 点传火系统的模拟试验装置

图1 为试验装置实物图，主要由金属套筒、前堵头、后堵头、固定支架、可视化药室、击发机构、中心点传火管等组成，装置右端的后堵头为泄压堵头，用来对整个装置进行泄压，保证气体安全有效地排出。图2为试验所采用的中心点传火管。点传火管全长268 mm，点火管的壳体内径18.5 mm，外径23 mm，四周开有不同排序方式的传火孔，即：沿传火管周向有4 列传火孔，每列分别有3 个或4 个传火孔，每个传火孔的孔径为6 mm，共计14 个传火孔。其中，首孔与底火端面的距离为120 mm，其余每个传火孔按40 mm 等距离分布。且传火管内装有苯奈药条，药条长约250 mm。为保证主装药点传火过程的安全性，实验主装药采用模拟发射药及少量真药混合装填的方式，其中模拟发射药比重、形状与真实发射药相当，模拟药粒直径为8 mm，高为13 mm，以保证装填后孔隙率与真实药床接近。模拟发射药与真实发射药体积比为42∶1，且模拟药粒的强度较真实发射药高，不易破碎，也不易燃烧。药室由耐高温高压的可视化有机玻璃制成，长为490 mm，内径为110 mm。

图1 密实装药床点传火试验装置实物图1—前堵头，2—上固定支架，3—金属套筒的后堵头，4—破孔压螺，5—可视化药室，6—金属套筒，7—下固定支架，8—击发机构Fig.1 Physical drawing of test device 1—front plug，2—upper fixing bracket，3—rear plug of metal sleeve，4—hole breaking pressure screw，5—visual chamber，6—metal sleeve，7—lower fixing bracket，8—firing mechanism

图2 中心点传火管实物图Fig.2 Physical drawing of central point fire pipe

图3 为试验测试系统示意图，系统通过电点火的方式击发点传火实验装置的底火，进而引燃点传火管内的苯萘药条。药条燃烧后，产生的高温高压火焰由传火孔喷入药室内，在药室中进行传播。试验时，采用高速摄像仪记录点火火焰在药床中传播的序列过程。同时，装置顶端开设4 个测压孔，首个测压孔与左端底火的距离为140 mm，且每两个相邻测压孔的间距约为100 mm，用以记录药室内不同位置测压孔的压力变化情况，揭示点火药气体进入药室后的传火规律。

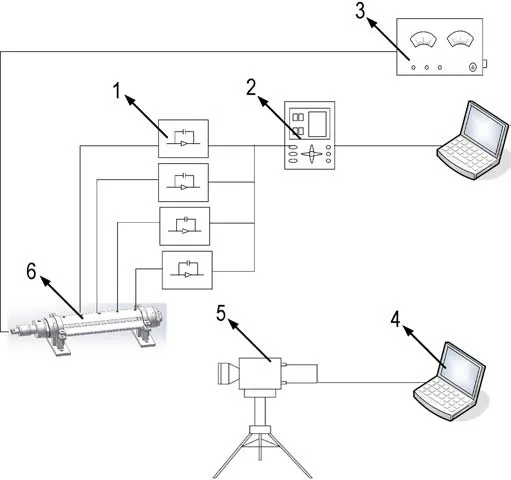
图3 密实装药床点传火试验测试系统示意图1—瞬态记录，2—电荷放大器，3—脉冲电点火装置，4—电脑，5—高速录像系统，6—点传火实验装置Fig.3 Schematic diagram of test system 1—transient recording，2—charge amplifier，3—pulse electric ignition device，4—computer，5—high speed video recording system，6—ignition and propagation experimental device

3 密实装药床点传火过程的数值仿真模型

3.1 物理模型

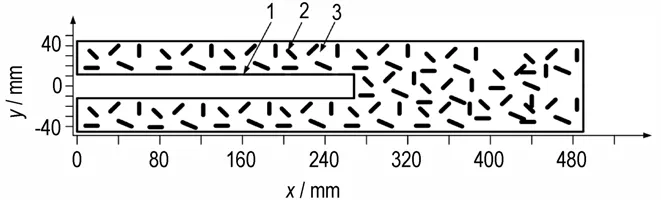
图4 密实装药床点传火物理模型示意图1—中心点传火管，2—模拟发射药粒，3—药室Fig.4 Schematic diagram of the ignition and propagation physical model of dense charge bed 1—central ignition tube，2—granular propellant simulant，3—chamber

在模拟实验的基础上，针对上述密实装药床点传火的物理模型，采用如下简化假设：

（1）由于试验中可视化药室材料的特殊性，点火燃气与壁面换热极少，故忽略点火药燃气与药室壁面的换热作用；

（2）为方便计算，将点火药燃烧产生的气体视为理想气体；

（3）忽略气体辐射和颗粒在高温下可能产生的催化效应；

（4）忽略热弥散效应；

（5）药室由球形的刚性假药粒填充而成，假药粒是均匀分布的灰体；

（6）药室壁面边界无滑移且绝热；

（7）整个点传火过程发生时间极短，火焰传播速度快，故忽略重力的作用。

3.2 数学模型

基于以上简化假设，建立下述基本控制方程［6］：

连续性方程：

式中，C为气体的比热容，J·（kg·K）-1；V为气体的体积，m3；T为 气 体 的 温 度，K；λ为 气 体 的 导 热 系 数，W·（m·K）-1。

3.3 多孔介质模型

从结构上来看，发射药粒在药室内填充构成的填充床结构，属于颗粒性多孔介质，因此采用多孔介质模型进行计算。对于一般的多孔介质模型方程，对其进行模块化和求解较难，因此这里利用N-K 湍流模型，将多孔介质模型改写为动量方程的同时，对动量方程中的雷诺应力进行模化，转化为输运方程，湍流对动量方程的影响等效为有效黏性系数，体现在输运方程中，用以模拟假药粒对流体流动的阻碍。在圆柱坐标系下，动量阻力项方程如（4）式［7］：

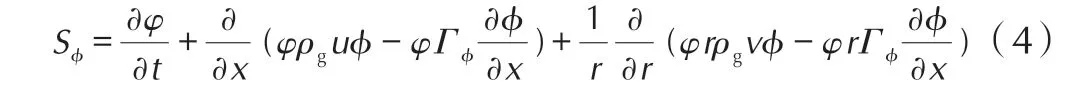
式中，Γφ为湍流的有效扩散系数，φ为时间平均项，x和r分别为圆柱坐标系的轴向坐标和径向坐标。将（4）式分解成分别为x和r方向上动量阻力方程［3］：

式中，D为颗粒的平均直径，mm；uˉ为本征平均速度，m·s-1。

因此，针对该填充床结构的多孔介质模型，改变渗透率K和惯性项系数b的值，将影响药室中假药粒对高温高压燃烧气体的阻碍作用。K和b通过Kuwahara等［8-10］总结的经验公式计算：

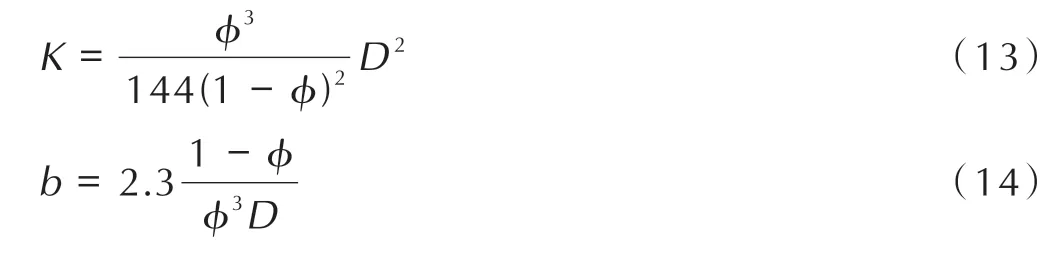
3.4 计算域

图5 为所研究的主装药床计算域。计算域采用结构化网格，经网格无关性验证后，取传火孔处网格尺寸为0.2 mm，其余的网格尺寸为0.5 mm，共计96896 个网格单元。求解时选择基于压力求解器，时间步长取1×10-5s，并经过了时间步长无关性验证。

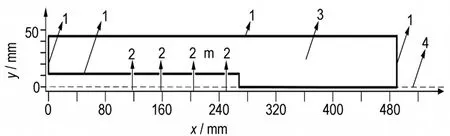
图5 流体计算域网格二维视图1—入口边界，2—药室内网格，3—墙体固定边界，4—对称边界Fig.5 2D view of grid in fluid computing domain 1—entrance boundary，2—chamber interior grid，3—fixed boundary of wall，4—symmetric boundary

3.5 初始条件与边界条件

药室内初始环境压力为101325 Pa，温度为300 K。根据经典内弹道理论［6］计算，中心传火管内燃烧气体产物的温度大致在2000～2500 K，因此传火孔入口气体温度设置为2500 K。结合试验用模拟发射药尺寸，颗粒等效粒径设置为12 mm。实际药床内孔隙率计算公式［11］为：

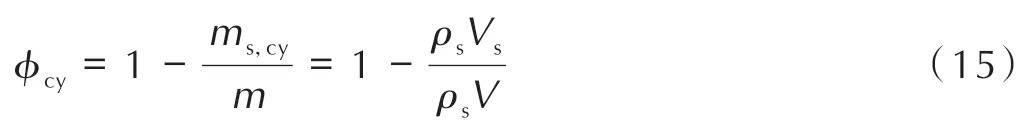
式中，φcy为填充床内孔隙率；ms，cy为实际填充床 内颗粒总质量，kg；m为药室内填满颗粒时相应质量，ρs为模拟发射药颗粒密度，kg·m-3；Vs为发射药颗粒体积，V为药床内总容积，m3。根据文献［12］可知，颗粒等效粒径为12 mm 时，其自然堆满整个药室的平均孔隙率为0.157。而本试验中，主装药的装填密度为0.7 kg·dm-3，主装药床的容积经计算为4.545 dm3，模拟发射药密度为1400 kg·m-3。由（15）式可知该试验的孔隙率为φ=0.41。

如图5 所示，药室壁面设为墙体固定边界，边界无滑移且绝热；中心传火孔采用质量流量入口条件，每个传火孔的质量流量均匀分配，并通过中心传火管的一维两相流方程计算出该质量流量。

4 模拟结果与对比分析

4.1 计算模型验证

结合上述所建立的模型，对试验工况下的点火过程进行了相应的数值模拟。图6 为利用高速摄像所拍摄的点传火序列图，图7 为仿真计算所得到的温度云图。由图6 可知，整个过程火焰发展均匀，火焰阵面清晰，点火火焰能够快速且均匀沿药床的轴向和径向传播。如图6a 所示，传火孔打开后，t=3.2 ms 时，拍摄到的图像中火焰面不明显，但可以观察到径向火焰面的发展较轴向更快。如图6b 所示，点火管内的点火药生成燃气通过传火孔向外喷射，已形成明显的火焰面，火焰面沿径即将接触药室壁面。如图6c 所示，此时中心传火管传火孔全部打开，且火焰面已沿径向充分扩展至药室壁面，而轴向还未充分扩展，但发展速度显著加快。当t=16.2 ms，图6d 中火焰面沿轴向和径向基本上充满整个药室。对比图6e 和图6f 可以发现，21.2 ms 以后，火焰阵面已经发展非常缓慢，药室两端堆积了大量假药粒。

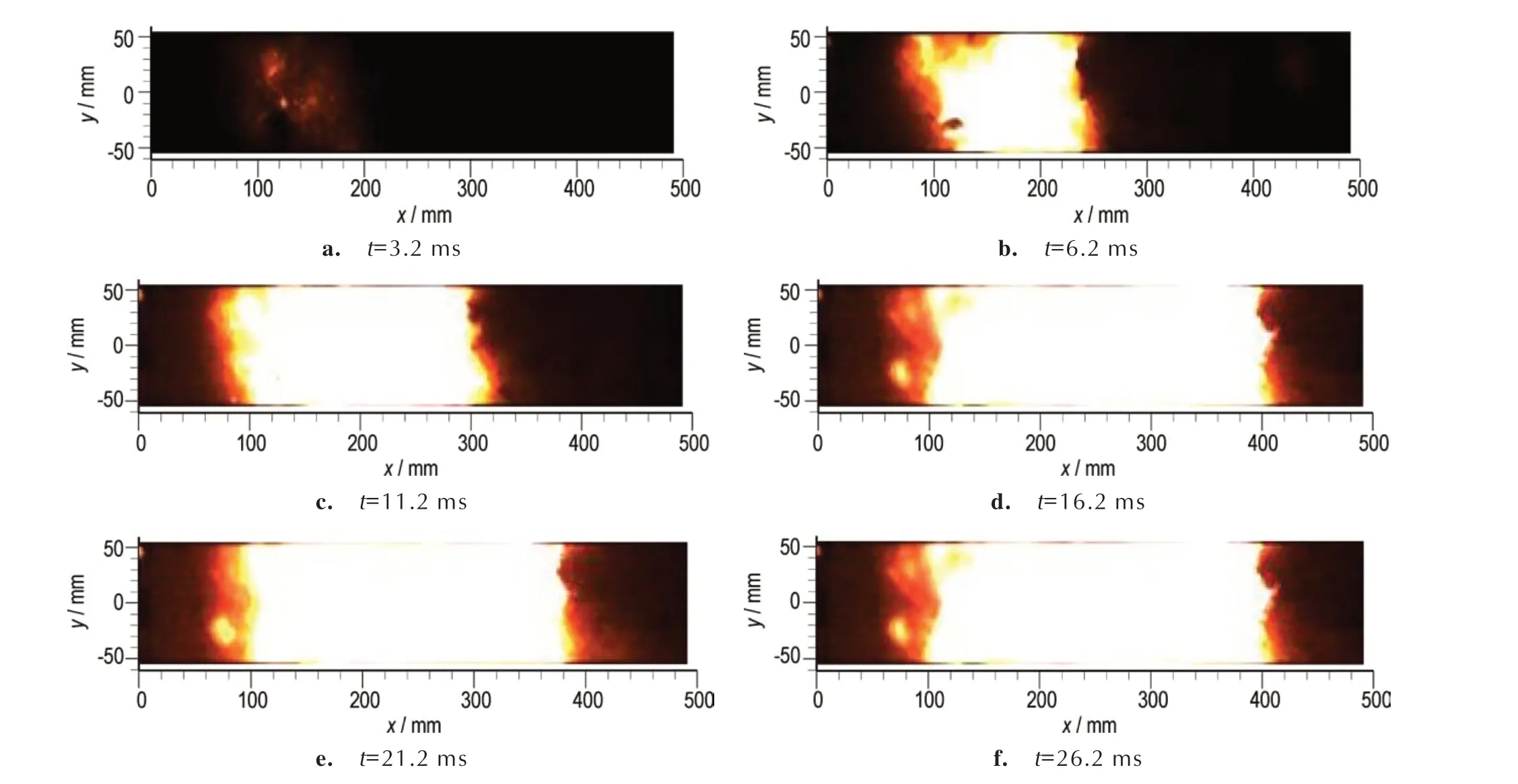
图6 部分点传火序列图Fig.6 Partial ignition and propagation sequence diagram

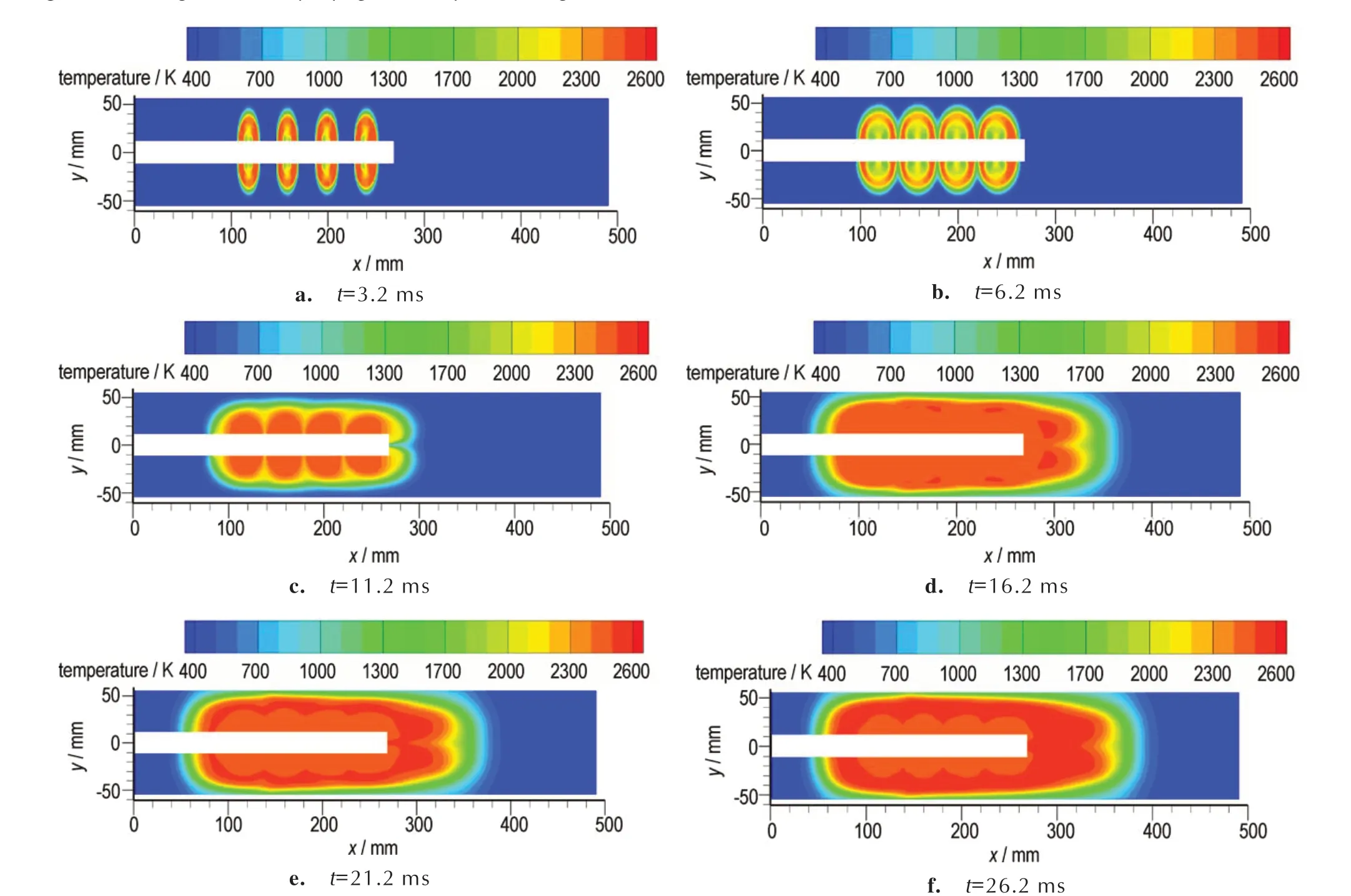
图7 仿真计算温度云图Fig.7 Temperature nephogram of simulated calculation

由图7 可知，数值计算得到的温度云图与试验拍摄图像具有良好的一致性。为验证这一结论，利用数值计算得到的温度场等温面近似等效于火焰阵面，分别获得了如图8 和图9 所示的试验和数值模拟的火焰阵面轴向和径向位移对比曲线图。由图8 可知，t=3～10 ms 时，轴向位移的增长速度较快，试验和仿真的轴向位移增长趋势一致，最大差值为4.02 mm，误差为1.8%；t=10 ms 后仿真火焰阵面落后于试验，原因为试验设有泄压装置，减小了实际火焰的轴向传播阻力，但仿真得到的等温面传播趋势和试验火焰阵面仍基本一致，最大差值为24.35 mm，误差为6.4%。图9 为火焰阵面径向传播位移随时间的变化曲线。仿真计算得到的等温面的径向位移在t=2.4～3.0 ms 时稍落后于试验，最大差值为3.37 mm，误差为8.6%。结合图7～图9 可知，药室径向尺寸远小于轴向尺寸。如图7a 所示，t=3.2 ms 时，火焰阵面已沿径向接近药室壁面，但每个传火孔所产生的火焰还未交汇，每簇火焰中心间距大，火焰轴向宽度小，火焰阵面沿轴向的发展相对落后，因此如图6a 所示，未交汇的火焰导致拍摄序列图中火焰面不明显。因此，数值模拟结果与试验吻合较好，验证了所建立模型的合理性。

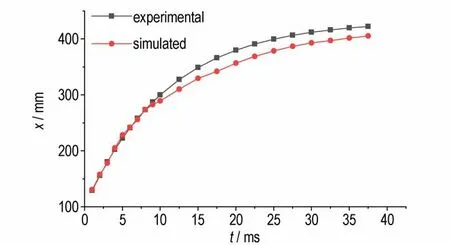
图8 火焰阵面轴向位移-时间试验与模拟对比曲线Fig.8 Comparison of axial displacement histories of flame front between experiment and simulation

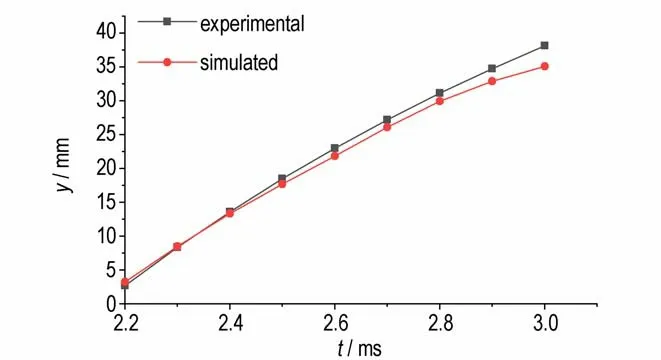
图9 火焰阵面径向位移-时间试验与模拟对比曲线Fig.9 Comparison of radial displacement histories of flame front between experiment and simulation

图10 为测压孔1 和2 处对应的数值计算及试验测得的压力对比曲线图。由图10 可知，试验中，t=0～7 ms时，测压孔1、2 压力基本相等，二者在7～8 ms 开始有了明显的区别，由于药室的右端设有泄压装置，所以距离泄压装置较近的测压孔2 最终压力略小于测压孔1，t=15 ms 时，测压孔1 压力为1.20 MPa，测压孔2 压力为0.90 MPa。数值计算测得的压力变化趋势与试验吻合，但后期计算得到的压力略大于实验，测压孔1 仿真计算结果与实验最大差值为0.07 MPa，误差为6.4%；测压孔2 与实验最大差值为0.07 MPa，误差为7.6%。因此，综上所述，所建立的模型可靠，可用于模拟点火火焰在药床中的传播特性。

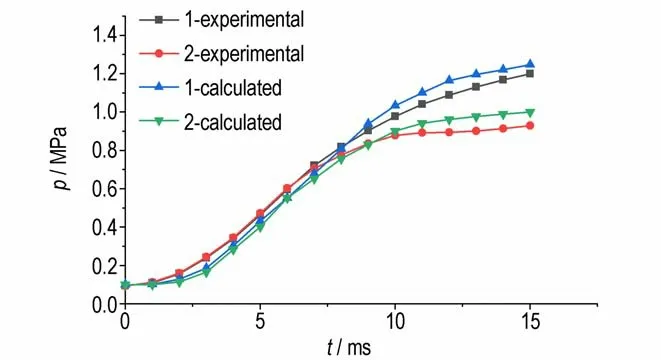
图10 两处测压孔的试验与模拟曲线对比Fig.10 Comparison of pressure histories of two gauges between test and simulation

4.2 孔隙率对火焰传播及压力影响的特性

为了研究不同装填密度下，点火药燃气在主装药床中的传播特性，针对不同孔隙率进行了多工况的数值模拟。过小的孔隙率差异将导致模拟计算所得结果的差异很小，难以进行比较，因此选择φ=0.30、φ=0.41和φ=0.50 这3 种数值模拟效果较好、计算所得物理参数差异明显的孔隙率进行分析，其中φ=0.41 为真实的试验工况。

图11 为计算获得的不同孔隙率下药室内火焰阵面轴向传播位移随时间的变化图。由图11 可知，t=37.5 ms 时，对于φ=0.30，火焰阵面轴向扩散位移为392.2 mm；对于φ=0.41，其轴向位移为405.2 mm；对于φ=0.50，其轴向位移为425.3 mm。且任意时刻下，孔隙率越大，火焰阵面沿轴向的扩展位移也越大；另外，可以明显发现，任意孔隙率下，t=0-10 ms 时，轴向位移的增加速度明显。图12 为计算获得的不同孔隙率下火焰阵面轴向传播速度的变化图。由图12 可知，计算初始时刻，φ=0.30 时，火焰阵面的传播速度为24 m·s-1，φ=0.41 时，其 传 播 速 度 为27.5 m·s-1，φ=0.50 时，其传播速度为30 m·s-1，孔隙率越大，火焰阵面沿轴向的传播速度也越大。当t=0～10 ms，轴向速度较大但以较快的速度减小，而随着时间的扩展，t=10 ms 后，速度变化率减小，轴向速度较小，因此结合图11 可知，t=0-10 ms，火焰阵面轴向位移的发展速度快，t=10 ms 后发展速度减缓。最终3 种孔隙率的传播速度都趋于2～3 m·s-1。产生上述变化的主要原因是药床内颗粒装填密度的变化引起了初始孔隙率的变化，孔隙率影响了火焰传播过程中药床内的阻力。孔隙率越大，点火传播过程中药床内的轴向阻力越小，火焰阵面沿轴向传播的初始速度越大，火焰阵面越快到达药室右端壁面；但孔隙率的变化基本不影响火焰阵面t=10 ms 以后的轴向传播速度。

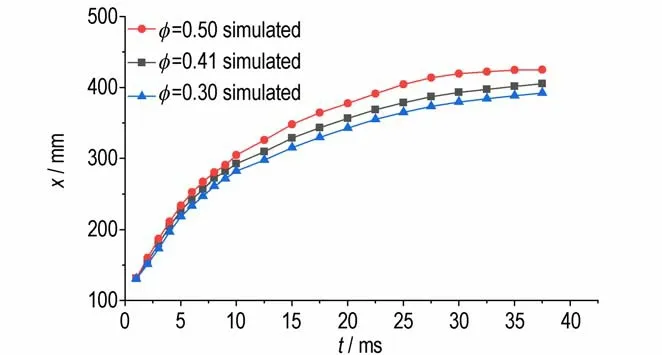
图11 模拟计算不同孔隙率轴向位移变化的对比Fig.11 Comparison of axial displacement changes with different porosities from simulated calculation

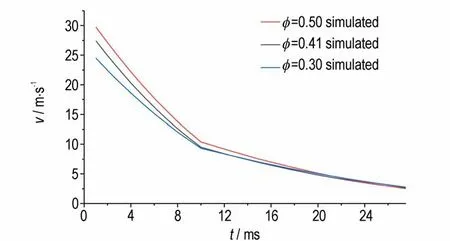
图12 模拟计算不同孔隙率的轴向速度变化的对比Fig.12 Comparison of axial velocity changes with different porosities from simulated calculation

图13 为不同孔隙率下药室内火焰阵面径向传播位移随时间的变化图。火焰阵面径向位移的发展集中在t=2.2-3 ms。由图13 可知，t=3.0 ms 时，对于φ=0.30，火焰阵面的轴向扩散位移为32.2 mm；对于φ=0.41，其轴向位移为35.0 mm；对于φ=0.50，其轴向位移为37.6 mm。且任意时刻下，孔隙率变大，火焰阵面沿径向的扩展位移也越大。图14 为计算获得的不同孔隙率下火焰阵面径向传播速度的变化图。由图14 可知，初始时刻，φ=0.30 时，火焰阵面径向传播速度最小，为51.1 m·s-1；φ=0.50 时，其 径 向 传 播 速 度 最 大，为52.8 m·s-1。随着时间的扩展，3 种孔隙率下，火焰阵面的径向传播速度迅速变小，当t=3 ms，径向速度都将减小到20～22 m·s-1。火焰阵面沿径向更早到达药室壁面，主要原因除了上述分析的药室径向尺度远小于轴向外，另一个原因在于火焰阵面的径向传播速度远大于轴向传播速度。综合轴向和径向的位移与速度曲线图，表明点火火焰传播过程中，孔隙率影响了药床内轴向和径向的阻力，促进火焰在药床内沿两个方向的均匀扩散传播；孔隙率越高，轴向和径向阻力同时减小，这有利于火焰阵面的快速传播。

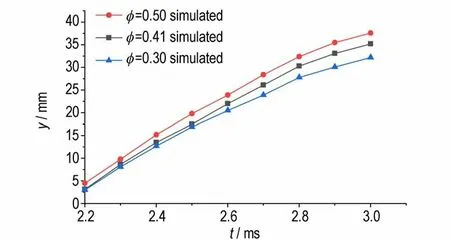
图13 模拟计算不同孔隙率径向位移变化的对比Fig.13 Comparison of radial displacement changes with different porosities from simulated calculation

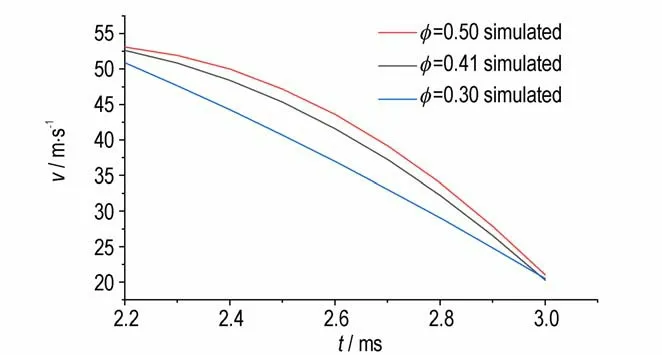
图14 模拟计算不同孔隙率的径向速度变化的对比Fig.14 Comparison of radial velocity changes with different porosities from simulated calculation

图15 和图16 分别为计算获得的不同孔隙率下，测压孔1、2 处对应的压力变化对比曲线。由图15 和图16 可知，任意时刻下，对应测压点的压力随着孔隙率的增大而减小。对于φ=0.30，测压点承压最大，且在该孔隙率条件下，t=15 ms 时，测压孔1 压力为1.31 MPa（图15），测压点2 压力为1.06 MPa（图16）；对于φ=0.41，测压点1 压力为1.21 MPa（图15），测压点2 压力为0.99 MPa（图16）；对于φ=0.50，测压点承压最小，测压点1 压力为1.16 MPa（图15），测压点2压力为0.96 MPa（图16）。主要原因是孔隙率的变化导致主装药床内气体容积的变化，孔隙率减小意味着气体容积的减小，点火药燃气进入药室后，迅速充满药室内的气体空间，进而导致压力也随之迅速升高。

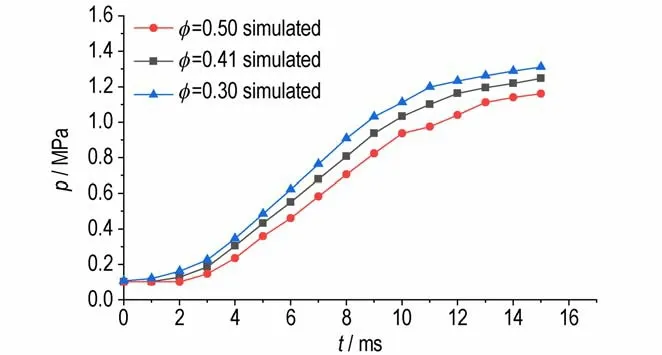
图15 模拟不同孔隙率下测压孔1 压力变化的对比Fig.15 Comparison of pressure changes of pressure gauge 1 with different porosities from simulation

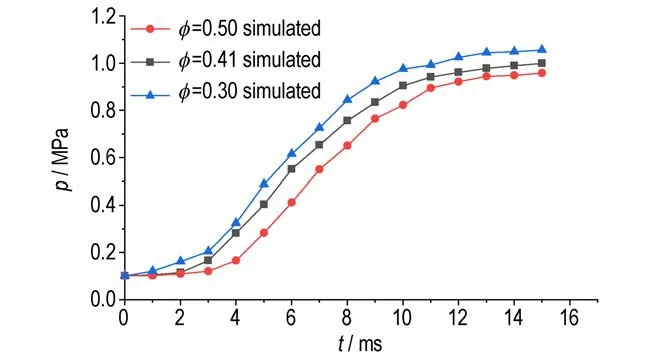
图16 模拟不同孔隙率下测压孔2 压力变化的对比Fig.16 Comparison of pressure changes of pressure gauge 2 with different porosities from simulation

综上所述，孔隙率的大小影响药床内不同位置压力的大小，而这就进一步影响火焰传播的均匀和瞬时性。综合图15 和图16 可知，φ=0.30 时，测压孔1 和2的压力差最大值为0.24 MPa；φ=0.41 时，测压孔1 和2 的压力差最大值为0.22 MPa；φ=0.50 时，测压孔1和孔2 的压力差最大值为0.20 MPa。3 种孔隙率下压力差最大值都是在t=16 ms 时产生的。两处测压点的同一时刻下压力差值较小，意味着点火的均匀性和瞬时性较好，而孔隙率越大，压力差越小。

5 结论

（1）仿真计算得到的药室内温度云图与试验中记录的火焰传播序列图呈现良好的一致性；两者火焰阵面沿轴向与径向位移最大误差分别为6.4%和8.6%；同时，数值计算和试验得到的药室内不同位置的压力曲线也吻合较好，最大误差为7.6%。因此，所建立的模型可靠，可用于模拟点火火焰在药床中的传播特性。

（2）在不考虑发射药燃烧的情况下，改变装填密度，针对孔隙率φ=0.30、0.41，0.50 进行了多工况的数值模拟。结果表明，在模拟计算的3 种孔隙率条件下，t=3～10 ms 时，火焰阵面轴向位移的发展较快，随着时间的发展，轴向速度由25～30 m·s-1减小到10 m·s-1，而t=10～40 ms 轴向速度逐渐减小到2～3 m·s-1；同样，在任意孔隙率条件下，火焰阵面径向位移的发展集中在t=2.2～3 ms，且t=3 ms 时径向速度都将减小到20～22 m·s-1，但较大的孔隙率初始时刻的径向速度大。孔隙率越大，点火传播过程中药室内火焰阵面的轴向和径向阻力减小，火焰阵面沿轴向的扩展位移越大，轴向和径向上的火焰传播初速度也越大。另外，除火焰阵面位移和速度的发展外，孔隙率越大，药室内的压力越小，当φ由0.30 增至0.41，由0.41 增至0.5 时，药室内不同位置处的压力差分别由0.24 MPa 减小到0.22 MPa、0.22 MPa 再减小到0.20 MPa，压力差稳定变小，且共减小了16.7%，也就是说，点火的均匀性和瞬时性提高。因此，提升主药床的装填密度的同时，更应注意点火时的均匀性。