微流挤出成形工艺挤出胀大机理研究

孔劲松，孙文彬，周 婧，段国林

（1.河北工业大学机械工程学院，天津300130；2.天津科技大学机械工程学院，天津300222）

1 引言

近年来，陶瓷材料在航天，医疗，生物等多个领域得到广泛应用，由于传统陶瓷成形工艺的成形时间较长，成形过程复杂，越来越多的快速成形工艺被用来制造陶瓷产品，微流挤出成形（Mi⁃cro-Flow Extrusion）就是其中一种［10］。与传统陶瓷成形工艺相比，陶瓷的微流挤出成形不需要传统陶瓷成形过程中的模具，具有成形效率高，成本低，成形过程简单，适应性广的优点。将陶瓷微流挤出成形与3D 打印技术结合形成的陶瓷浆料3D 打印（3D Printing of Ceramic Paste），可实现复杂陶瓷产品的快速成形［9］。

在陶瓷浆料3D打印的挤出过程中，陶瓷浆料在挤出口处会发生挤出胀大现象（Extrusion Swell），导致挤出丝的形状发生改变，降低了陶瓷产品的成形精度。相关人员对挤出胀大现象进行了研究：文献［1］研究了高填充性聚丙烯基纳米复合材料加工过程中的挤出胀大现象；文献［2］研究了挤出口模结构对挤出物形状的影响；文献［3］建立了似膏体浆料的粘弹性流变模型；文献［4］研究了陶瓷浆料挤出过程中的流变行为。目前对挤出胀大现象的研究多集中在橡胶，塑料等高分子聚合物材料，对陶瓷浆料的挤出胀大现象研究较少；对陶瓷浆料流变行为研究方法多集中于仪器测量，通过计算机仿真的方法对陶瓷浆料流变行为进行研究的较少。

这里应用计算机对陶瓷浆料的挤出过程进行仿真，通过建立挤出力学模型；对多组流道组合进行模拟分析；对挤出压力和挤出口挤出速率进行计算；揭示陶瓷浆料挤出胀大机理，得出陶瓷浆料挤出胀大现象和流道结构的关系。研究得到的结论对优化陶瓷浆料3D打印工艺参数，提高陶瓷3D打印成形精度具有一定的指导意义。

2 理论分析

2.1 陶瓷浆料的挤出过程

陶瓷浆料微流挤出成形示意图，如图1所示。外力推动柱塞杆挤压料筒内的陶瓷浆料，陶瓷浆料在挤压力作用下经过挤出头挤出形成挤出丝。陶瓷浆料3D打印就是将挤出丝按照一定的顺序和形状堆积叠加，最终形成陶瓷产品［7］。

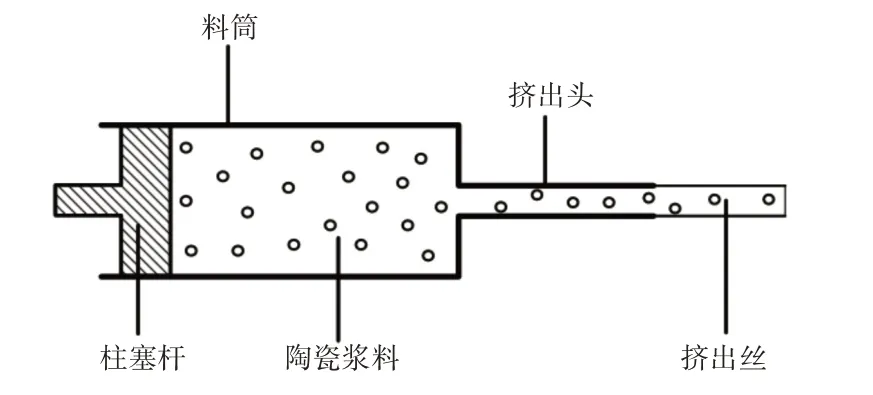
图1 陶瓷浆料微流挤出成形示意图Fig.1 Diagram of Ceramic Paste Micro-Flow Extrusion Forming

陶瓷浆料在挤出过程中表现有固体的弹性特性，当浆料受力流动情况突然变化，如浆料挤出的开始、停止，或是在流道截面发生变化处，例如挤出头挤出口、料筒和挤出头的过渡段，陶瓷浆料都会表现出很强的弹性效应［4］。

不同性质的流体在流道挤出口处的变化情况，如图2所示。牛顿流体挤出的过程中，由于重力的作用，在挤出口处挤出段的截面变小，而粘弹性流体在离开挤出口后，由于流道的截面发生变化，表现出弹性效应，产生弹性回复，挤出段发生膨胀，挤出段的截面变大，这种现象就是挤出胀大，又称为巴勒斯效应（Barus Effect）［11］。陶瓷浆料在挤出过程会产生挤出胀大现象，这种现象反映出陶瓷浆料本质是一种粘弹性流体，挤出胀大率是反映陶瓷浆料挤出胀大程度的参数。如式（1）所示，为挤出胀大率的计算公式。

图2 不同性质流体在挤出口变化Fig.2 Different Properties of the Fluid at the Extrusion Outlet Change

式中：B—挤出胀大率；Dmax—挤出胀大段直径；D0—挤出口直径。

陶瓷浆料的微流挤出成形过程中伴随着较为复杂力学变化，可以建立的陶瓷浆料微流挤出力学模型对浆料挤出过程进行描述，如图3所示。柱塞杆刚开始挤压陶瓷浆料，此时陶瓷浆料的内部应力未达到屈服应力τb，开关处于常开状态，陶瓷浆料只发生弹性形变进行弹性储能，不发生流动。由于浆料存在粘性作用，弹性形变是一个逐步增加的过程，此时陶瓷浆料内部的应力为弹性应力与粘性力之和，用一储能元件K和一粘性元件C1并联表示（图3模型中开关左半部分）；当柱塞杆继续挤压陶瓷浆料，陶瓷浆料被进一步压缩，陶瓷浆料的内部应力超过屈服应力τb，开关闭合，浆料开始流动。流动时受到流动粘性力的作用，用另一个粘性元件C2表示，此时陶瓷浆料的内部应力为流动粘性力，用开关闭合状态下的整个模型表示。

图3 陶瓷浆料微流挤出力学模型Fig.3 Mechanical Model of Micro-Flow Extrusion of Ceramic Paste

2.2 数学模型

由上述分析可知，陶瓷浆料的挤出是一个逐渐达到稳定的过程，陶瓷浆料在未开始流动时只进行压缩储能，浆料宏观表现纯粘弹性。当内部应力达到一个值后开始流动，浆料宏观表现流动粘性，最终稳定挤出。稳定挤出时浆料内部应力需要用一个数学模型描述。

在粘弹性流体模型中，Oldroyd-B模型将流体内部应力分解为纯粘弹性和流动粘性两个部分，和材料本身三个参数（零剪切粘度，松弛时间，延迟时间）有关，可以定性描述粘弹性流体的宏观性质，因此，陶瓷浆料稳定挤出时内部应力采用Oldroyd-B 模型描述。所采用三维Oldroyd-B粘弹性模型［12］的数学表达形式为：

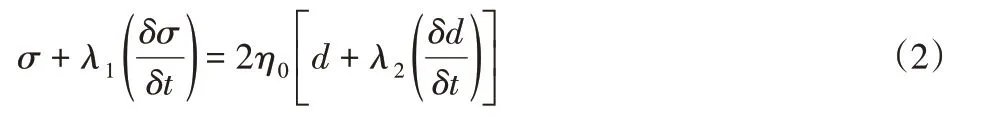
三维中陶瓷浆料内部应力用张量形式表示，式中：σ—张量中的偏应力张量；δσ/δt—偏应力张量对时间偏微商；d—形变率张量；δd/δt—形变率张量对时间偏微商；η0—浆料的零剪切粘度（Pa·s）；λ1—浆料松弛时间（s），λ1=0时，浆料变成牛顿流体；λ2—浆料延迟时间（s），λ2=0，浆料变成Maxwell流体［13］。

挤出过程中陶瓷浆料在料筒壁面存在滑移现象，壁面附近的浆料沿挤出方向存在剪切应力，这种现象同样会影响浆料的挤出胀大情况。考虑到陶瓷浆料在壁面处的滑移情况，采用描述粘弹性流体壁面处滑移的Navier模型来模拟陶瓷浆料在壁面处的滑移情况［2］：

式中：f（v）—浆料在壁面处的剪切应力；v—浆料的切向速度（m/s）；vwall—壁面的切向速度（m/s）；k、e—与陶瓷浆料有关的参数。

3 挤出过程模拟分析

3.1 仿真组合的正交试验设计和参数选择

通过对陶瓷浆料挤出过程分析，可以知道陶瓷浆料的挤出胀大效应是由浆料在挤出过程中的弹性储能造成；弹性储能量和挤压力是正相关。Benbow-Bridgwater挤压力模型［4］，根据此模型可以得到挤压力与流道结构参数关系，如图4所示。

图4 Benbow-Bridgwater挤压力模型Fig.4 Benbow-Bridgwater Extrusion Model

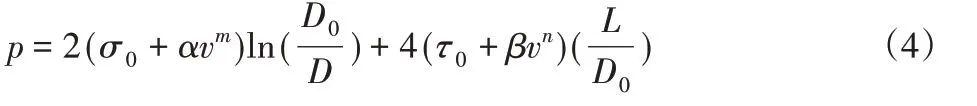
式中：p—挤压力；σ0—初始入口屈服应力；α—入模屈服应力速度因子；v—为浆料挤出速度；τ0—初始模璧剪切应力；β—挤压段剪切应力速度因子；D—料筒直径；D0—挤出头直径；L—挤出头长度；m，n与速度因子α，β有关。

从式（4）可以看出挤压力和流道结构中的挤出头长度、流道截面比（料筒截面和挤出头截面比）有关。以挤出头内径，料筒内径和挤出头长度为变量，根据正交试验原理设计仿真组合，所使用的正交设计软件为Minitab，设计的仿真组合，如表2所示。选择的陶瓷浆料为水基氧化锆（ZrO2）陶瓷浆料，氧化锆陶瓷浆料的优点有：无毒无污染；可在料筒中密封储存；在挤出后可以直接成形且可以保持一段时间的形状；陶瓷浆料在挤出成形后可以直接进行烧结［6］。仿真选用ANSYS软件，软件中粘弹性模型选择Old⁃royd-B 模型。制备固含量为65%的水基氧化锆陶瓷浆料，经流变仪测量，得到陶瓷浆料对应式（2）［12］中Oldroyd-B 粘弹性模型参数为η0=11950Pa·s，λ1=0.2 s，λ2=0.9s；设置式（3）［2］中壁面滑移参数为：e=0.08，k=4.5×103。浆料在流道内挤出流动的剪切速率在（45～350）s-1之间［5］，通过对氧化锆陶瓷浆料雷诺数的计算，判断氧化锆陶瓷浆料在流道内的流动状态为层流。

3.2 流道的建模和网格划分

如图1所示，陶瓷浆料3D打印微流挤出装置中的挤出机构由柱塞杆，料筒和挤出头组成。在实际打印中，所使用的料筒为美式点胶针筒，挤出头为点胶针头，均为标准型号，具有标准尺寸。其中，常用的点胶针头长度型号有0.25in，0.5in，1.0in，1.5in四种，直径型号有14G，18G，21G，23G四种，（其中点胶针头的直径型号对应不同的颜色，每种不同直径型号的点胶针头具有不同的长度型号，如图5 所示）点胶针筒容量型号有3cc，5cc，10cc，30cc四种，型号对应具体尺寸参数，如表1所示。

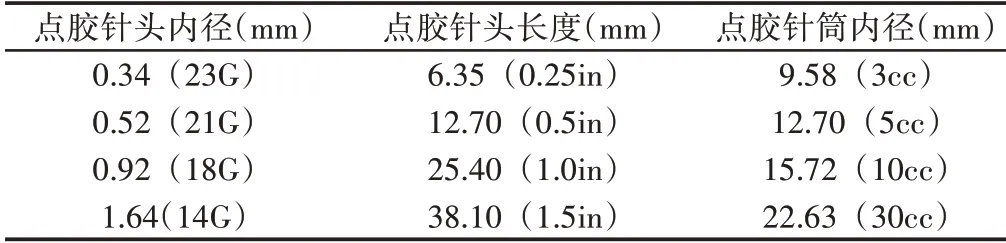
表1 点胶针头和点胶针筒的标准尺寸参数Tab.1 Standard Size Parameters for Dispensing Needles and Dispensing Syringes

图5 各种直径型号的点胶针头Fig.5 Sizes of Dispensing Needles of Various Diameters

以氧化锆陶瓷浆料入口流量为3mm3/s下的挤出过程为模拟研究对象，按照表2设计的组合建立出流道模型，以组合1的三维模型为例，挤出流道的3D模型和有限元网格模型，网格单元数目为56611，节点数目为68078，如图6所示。

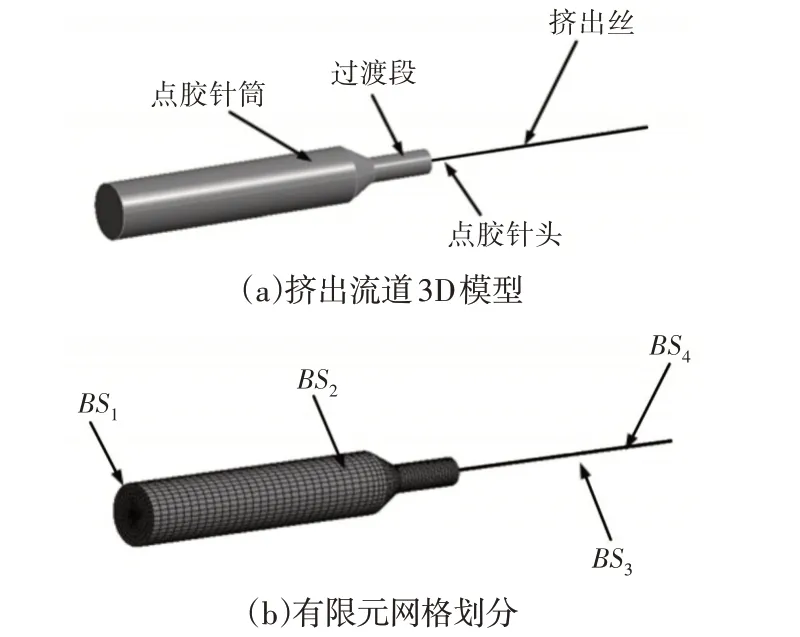
图6 挤出流道3D模型、有限元网格划分示意图Fig.6 3D Model of Extrusion Runner and Schematic Diagram of Finite Element Meshing

边界条件的设置如下所示：BS1：入口条件，入口流量为3mm3/s；BS2：壁面边界条件，采用Navier滑移条件；BS3：挤出物的自由表面；BS4：出口边界条件，fn=fs=0。

3.3 数值模拟结果分析

3.3.1 挤出胀大模拟结果分析

为了避免做多组仿真模拟试验，提高模拟分析效率，按照正交实验法设计仿真组合，并进行仿真模拟分析，正交试验法设计的仿真组合，如表2所示。

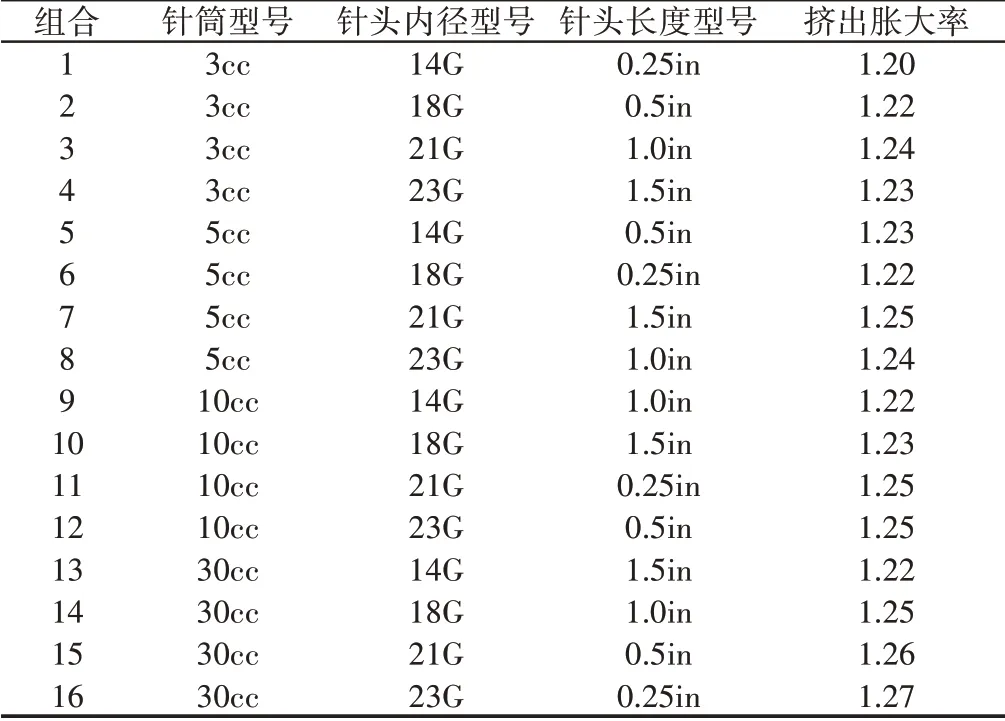
表2 仿真组合及结果Tab.2 Simulation Combination and Results

由式（1）可以计算得到挤出胀大率。对上述仿真数据利用正交分析软件Minitab进行分析。通过分析，截面比越大，陶瓷浆料挤出胀大率整体呈现增大的趋势，符合流道截面变化处浆料的弹性储能造成挤出胀大现象的分析；随着点胶针头长度的增加，陶瓷浆料的挤出胀大率出现先增加后减小的情况。下面通过对流道内挤出压力和点胶针头挤出口挤出速率的模拟分析来研究点胶针头长度对挤出胀大率的影响。

3.3.2 挤出压力分析

对上述组合中流道内的压力进行分析，组合1、组合5、组合9、组合13中陶瓷浆料挤出过程中流道内的压力云图，如图7所示。

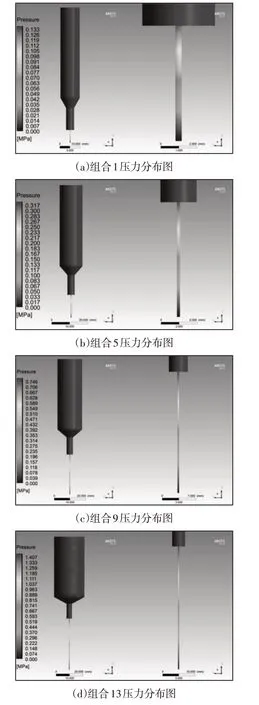
图7 挤出过程中不同流道内部的压力分布Fig.7 The Internal Pressure of Different Runner During Extrusion

从图7中可以看出陶瓷浆料在点胶针头内的压力是呈现阶梯状的变化，逐渐递减，这种分布符合前面计算判断陶瓷浆料在流道内为层流的流动特性。在不同的流道内，陶瓷浆料所需的挤出压力大小也不同，表现为点胶针筒直径与点胶针头直径比越大，点胶针头越长，陶瓷浆料所需的挤出压力越大。这是由于点胶针筒直径与点胶针头直径比越大，流道截面比也越大，陶瓷浆料的弹性储能量也变大，浆料需要的挤出压力变大；点胶针头长度越长，陶瓷浆料在点胶针头内的挤出阻力越大，浆料所需要的挤出压力也会变大［16］。

3.3.3 挤出口挤出速率分析

可以看出在上述仿真组合中，随着点胶针头的长度增加，出现陶瓷浆料的挤出胀大率先增加后减小的结果，可以得知点胶针头的长度对挤出胀大现象同样存在影响。选择表2仿真组合中的组合1，并将组合1中点胶针头长度改为1.0in作为对比组合，进行挤出口挤出速率的模拟。这两个组合挤出口挤出速率分布图，如图8（a）、图8（b）所示。从图中可以看出，挤出口处的等速度线呈现外凸形状。这是由于陶瓷浆料在料筒和挤出头的过渡段发生弹性储能，导致挤出头中在流动方向的法向上产生速度梯度，在挤出口陶瓷浆料发生弹性回复，引起出口截面上速度的不一致。对比这两个组合的挤出口截面上速率差，如图8（c）、图8（d）所示。挤出口由中心到边缘，速率逐渐递减。组合1速率差要比对比组合的大，组合1的挤出胀大率也较大。这个现象说明陶瓷浆料在点胶针头中流动时发生部分弹性回复，点胶针头越长，陶瓷浆料在点胶针头内的流动时间越长，陶瓷浆料的弹性回复程度也越大，造成对比组合中陶瓷浆料在挤出口处的挤出胀大率减小。

图8 点胶针头挤出口挤出速率分布Fig.8 Distribution of Extrusion Velocity of Dispensing Needle Outlet

4 挤出实验

4.1 挤出实验设计

微流挤出3D打印平台根据压力产生方式的不同可以分为机械式和气压式［8］，如图9所示。机械式微流挤出3D打印平台，在机械式打印平台中，微流挤出装置主要是由夹具，直线驱动器，压力传感器，柱塞杆，料筒，挤出头等组成，如图9（a）所示。直线驱动器的驱动电机采用42步进电机，电机经减速齿轮减速后，带动一对丝杆螺母，把42步进电机的旋转运动变成直线运动，利用42步进电机的正反转做推杆动作，推动柱塞杆挤压料筒内存储的陶瓷浆料，陶瓷浆料在压力的作用下直接挤出成形［15］。

图9 两种微流挤出3D打印平台Fig.9 Two Types of Micro-Flow Extrusion 3D Printing Platform

用固含量65%氧化锆陶瓷浆料进行挤出实验对上述分析结果进行验证。使用设备为机械式陶瓷浆料微流挤出3D 打印平台，如图9（a）所示。使用点胶针筒型号30cc，选择0.25in、0.5in和1.0in三种长度型号点胶针头（直径型号均为21G）。

实验方法为控制挤出速度为3mm/s，分别使用三种长度型号点胶针头，在相同路径规划程序下，打印出三个矩形长条块，对比三个矩形块高度，并通过压力传感器采集挤出过程的压力数据［14］。

4.2 挤出结果分析

打印过程中使用纽扣型压力传感器实时采集的挤出压力数据：陶瓷浆料挤出压力先逐渐上升，表现为弹性储能，如图10所示。达到一定应力值后开始流动，储存能量开始释放，能量减少，浆料再次压缩进行弹性储能，依此循环，最终挤出压力趋于稳定。挤出压力变化符合图3所示的陶瓷浆料微流挤出力学模型。

图10 不同长度型号点胶针头的挤出压力Fig.10 Extrusion Pressure of Different Length Sizes of Dispensing Needles

通过对比图10 的数据，可以看出来使用0.25in 长度型号稳定挤出压力约为240N，使用0.5in 长度型号稳定挤出压力约为300N，使用1.0in 长度型号稳定挤出压力为335N。这是由于点胶针头的长度越长，陶瓷浆料在点胶针头内的挤出阻力越大，浆料所需要的挤出压力也会变大，符合前面对挤出压力规律的分析。

在相同路径规划下使用三种长度型号点胶针头打印出三个矩形长条块，如图11（a）所示。用图11（b）所示的Smart Zoom5超景深3D形貌仪在相同角度和距离条件下拍摄三个矩形长条块的侧面，得到矩形块的侧面形貌图，并进行对比测量。

图11 打印的陶瓷矩形块和测量仪器Fig.11 Printed Rectangular Block and Measuring Instrument

三个矩形块侧面形貌，拍摄角度距离一致，观察拍摄到的图片，如图12所示。可以看出使用0.5in针头的挤出丝线宽大于使用0.25in针头挤出丝线宽，使用1.0in针头的挤出丝线宽小于使用0.5in针头的挤出丝线宽。这是由于点胶针头变长，挤出压力变大，浆料弹性储能量增加，挤出胀大率随之增大，挤出丝线宽增加；针头长度继续增加，陶瓷浆料在针头内流动时间变长，弹性回复程度增加，挤出胀大率反而会变小，导致挤出丝线宽减小。符合前面对挤出压力和挤出速度影响挤出胀大率规律的分析。

图12 矩形长条块侧面形貌图Fig.12 Profile Morphology of Rectangular Block

挤出实验得到的结果和模拟分析结果具有良好的一致性，说明模拟分析结果有效合理。

5 结论

基于对陶瓷浆料挤出过程的理论分析，模拟比较不同流道下陶瓷浆料挤出胀大率，并对挤出压力和挤出口挤出速率进行模拟分析，设计陶瓷浆料挤出实验，实验结果和模拟结果基本一致，说明模拟分析合理有效，得出以下结论：（1）陶瓷浆料的微流挤出是一个逐渐达到稳定的过程，未开始流动时只进行压缩储能，浆料宏观表现纯粘弹性。当内部应力达到一个值后开始流动，浆料宏观表现流动粘性。（2）流道截面突变处（料筒和挤出头之间的过渡段）的截面比越大，浆料的弹性效应越强，引起浆料弹性储能量增加，挤出胀大率变大；挤出头越长，陶瓷浆料在挤出头段流动时弹性回复程度越强，挤出胀大率减小。（3）在陶瓷浆料挤出成形过程中，通过调整流道的结构可以有效调控陶瓷浆料在挤出过程中的压力分布和流动速率分布，进而调节陶瓷浆料3D打印过程中的挤出胀大情况。