方差分析法下激光陀螺仪机械振动抑制技术

梁秀娟，嵇海旭

（广东海洋大学机械与动力工程学院，广东 湛江524008）

1 前言

激光陀螺仪现作为可以精确确定物体方位的仪器，其机械式的结构复杂，对导航系统的性能起到影响，可以利用激光陀螺仪抖动的进动性和定向性对空间的方位和转数进行测试，能够反映出陀螺仪抖动控制的变化，并且确定抖动的位置信息号。众多国家都投入了人力物力等条件对激光陀螺仪展开研究，将激光陀螺仪的机械抖动当作核心进行分析［1］。激光陀螺仪实际是一种光学振荡器，是利用光程差来测量旋转角的速度，当物体在高速转动时，转动轴会稳定的指向一个方向，这时，激光陀螺仪不仅可以保持方向的一定性，而且保持高速转动，在这个条件下的激光陀螺仪可以确定东西南北方向，直到精确得到正确方向；在地理方面，激光陀螺仪成为定向的主要仪器，则对激光陀螺仪的机械抖动控制技术的分析研究成为未来航空航海等领域的主要研究技术。

文献［2］将光纤陀螺仪应用到快速掘进系统导向过程中，通过设定光纤陀螺仪的俯仰角和横滚角精度，降低操作掘偏情况，提高连采掘进效率。文献［3］通过单一陀螺和双轴倾角传感器组合描述了一种桅杆式光电系统，与激光陀螺仪结合，应用惯性导航设备获得的本地坐标，将其应用在侦察定位中，提高定位精度。文献［4］根据光纤陀螺保偏光纤环分布偏振耦合测试数据的测量结果，建立了测量点偏振耦合幅度模型，通过提取真耦合位置和强度信息，对光纤陀螺零漂误差进行评测，评测结果表示光纤陀螺仪可精确分析零漂预估值。

由于以上研究并未涉及激光陀螺仪自身机械振动相关研究，且所提方法存在噪音干扰、稳定性低等问题，这里在提出基于方差分析法的激光陀螺仪的机械抖动控制方法。确定激光陀螺仪的机械结构，分析激光陀螺仪机械抖动控制的电路，利用方差分析法实现激光陀螺仪机械振动抑制。

2 激光陀螺仪的机械抖动控制

2.1 激光陀螺仪的机械动力模型

为了分析激光陀螺仪抖动机构的扭转抖动，设置一个弹簧阻尼系统，利用陀螺仪的总惯量和总刚度等条件建立抖动方程，分析激光陀螺仪的正弦抖动信号，对抖动轴的转角进行求解，当弹簧阻尼系统中陀螺仪分别为零初值时和有初值时［5-6］，利用la⁃place的变换和反变换计算激光陀螺仪的抖动输出，最终完成了激光陀螺仪机械动力模型的建立。所构建的激光陀螺仪结构示意图，如图1所示。

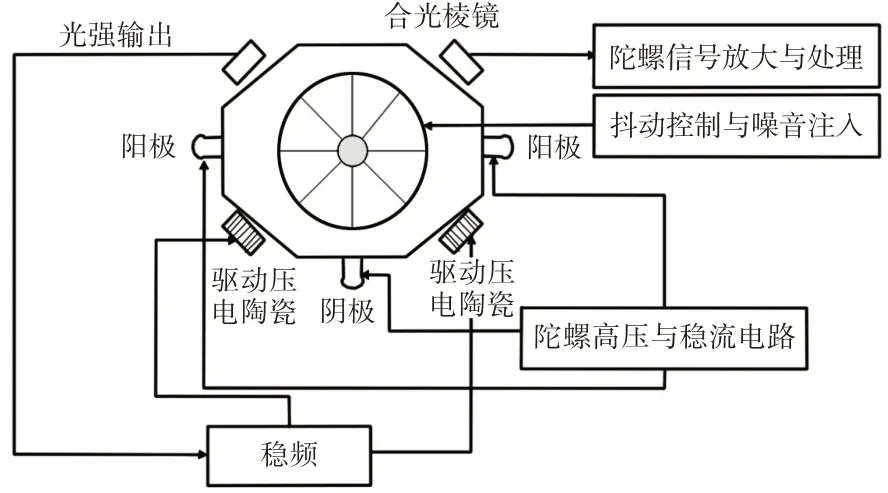
图1 激光陀螺仪结构示意图Fig.1 Structure of Laser Gyroscope

激光陀螺仪的主要部件有抖动机构，将抖动机构看做一个整体，分析抖动机构的扭转抖动，设有一个弹簧阻尼系统，对其抖动机构自由度的扭转抖动进行分析［7］，构建抖动方程为：

式中：J—激光陀螺仪抖动机构的转动总惯量；C—阻尼项；K—总刚度；θ—激光陀螺仪抖动轴的转动角度；M(t)—激光陀螺仪抖动的驱动力。对激光陀螺仪的正弦抖动信号进行分析［8］，则陀螺仪的驱动力与陀螺仪的正弦波相等，表达式为：

根据式（2）激光陀螺仪的正弦波驱动，通过解方程的方法对抖动轴的转角进行求解，可以将式（1）转换为：

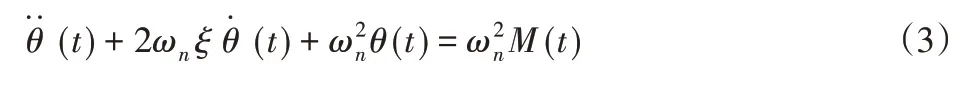
式中：ξ—激光陀螺仪的阻尼系数；

ωn—激光陀螺仪转动自然角的频率。

激光陀螺仪的因数Q通常为，在（80～305）之间，激光陀螺仪的阻尼系数在（0.003～0.006）之间［9］。为考虑其弹簧阻尼系统中陀螺仪的零初值，将式（5）进行laplace转换，能够得到θ(s)，表达式如下：

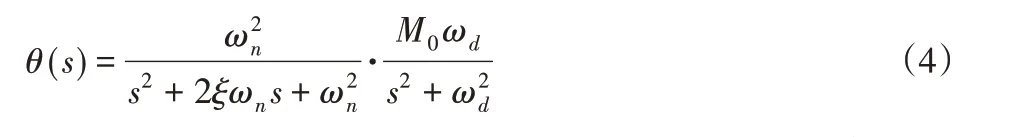
进一步对式（6）进行laplace的反变换，获得激光陀螺仪在机械时域中抖动轴转角的公式为：

激光陀螺仪抖动轴输出的角度包括瞬态和稳态响应，在启动机械激光陀螺仪抖动时，启动时抖动轴的过渡为瞬态响应，瞬态过程很短，完成启动后变为稳态，分析激光陀螺仪抖动的输出只有稳态响应，表达式为：

由于激光陀螺仪的阻尼系数ξ较小，可将稳态响应输出正弦波与输入正弦波信号相位差值，则。分析得知，在陀螺仪正弦动力下，输出的激光陀螺仪信号比频率相同，并且相位滞后了90℃［10-11］，其激光陀螺仪的幅值是输入陀螺仪信号频率的常值。当弹簧阻尼系统中陀螺仪有初值时，则θ(0)=，将式（2）代入式（3），利用laplace 的变换和反变换计算激光陀螺仪的抖动输出：

当有初值时只对瞬态响应有影响，并改变了到达稳态时间，结合上述计算，完成了激光陀螺仪的机械动力模型的建立，表达式为：

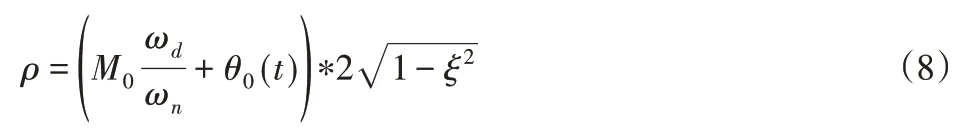
2.2 激光陀螺仪机械抖动控制的电路分析

基于以上激光陀螺仪的机械结构及动力模型分析，设计激光陀螺仪机械抖动控制的电路框图，如图2所示。

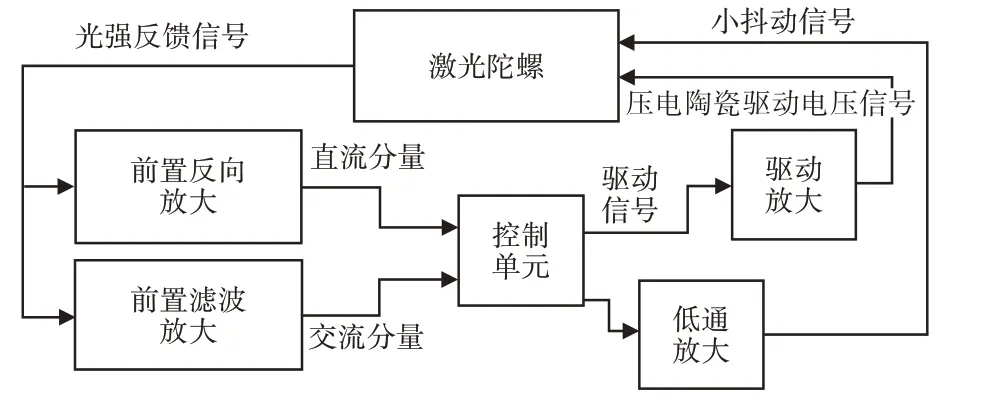
图2 激光陀螺仪机械抖动控制电路框图Fig.2 Control Circuit Diagram of Mechanical Jitter of Laser Gyroscope

为了避免激光陀螺仪闭锁产生的影响，利用机械抖动来减少陀螺仪的闭锁误差，陀螺仪抖动的速率小于闭锁的阈值，导致信号遗失，陀螺仪偏频抖动出现的闭锁现象为动态误差，计算公式如下：

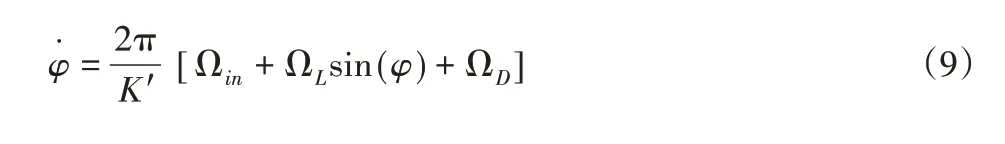
式中：K′—激光陀螺仪的系数；Ωin—激光陀螺仪的角速度；ΩL—陀螺仪的闭锁速率；ΩD—陀螺仪的峰值抖动速率。

陀螺仪机械抖动将原始的静态锁分割几个小的锁区，使激光陀螺仪偏离在锁区以外，减少了陀螺仪的封闭误差，导致动态闭锁误差的出现。为了对激光陀螺仪的特性进行改善，对其信号和幅度进行调节，使误差值可以接近零，对动态误差完成抑制。加入随机噪声，设激光陀螺仪的峰值抖动速率为α，噪声为ε，则有如下表达式：

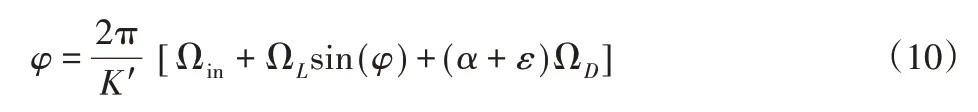
当α+ε变大时，在一些周期内完成解锁，噪声的引入可以在多个周期内，陀螺仪的动态闭锁消失，结合上述计算，完成激光陀螺仪机械抖动控制的电路分析：

2.3 方差分析法下激光陀螺仪机械抖动控制技术

在对激光陀螺仪建立机械动力模型和分析机械抖动电路的基础上，计算激光陀螺仪输出数据的平均角速率和平均角速度值，利用方差公式对其进行定义，获得激光陀螺仪抖动时间，并对激光陀螺仪中的误差源进行分离，最终实现激光陀螺仪的机械抖动控制技术。

对激光陀螺仪的机械抖动输出数据进行周期采样，机械抖动输出的是激光陀螺仪的脉冲数，将周期采样获得的脉冲数设为x，一共采集了N个激光陀螺仪的数据，将其分成N′组，每组中有M′个数据，则N=N′×M′，第j个输出数据的采样周期T的平均角速度是第j时刻角速率λj，表达式为：

式中：S′—激光陀螺仪的脉冲当量。

激光陀螺仪的每组数据的平均角速度值的计算公式为：

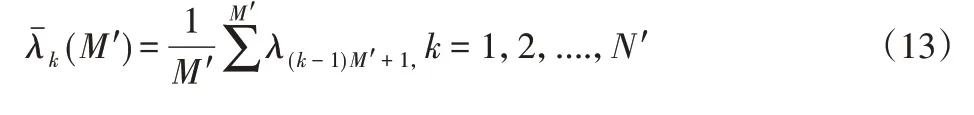
式中：k—数据组数，可用方差对其进行定义，公式如下：

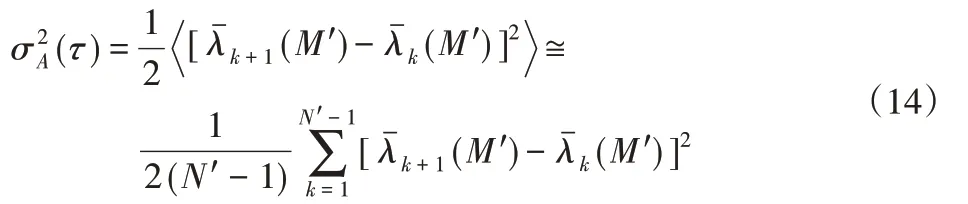
式中： —数据的总体平均；τ=M′×T—指定的激光陀螺仪抖动时间，且M′=1，2，...，Mm′ax、M′max≤，其中，M′max—最大值数据。式（13）和式（14）的递推式公式为：

式中：m—数据集，m=1，2，...，M′，利用递推式运算可以提高计算速度。假设激光陀螺仪中的各误差源是独立的，利用方差将激光陀螺仪中误差源方差的平方和进行计算，计算公式为：

方差较小，则拟合标准方差能够提高精度，拟合方程为：

式（17）和式（18）的计算可以将激光陀螺仪中的误差源分离，结合上诉分析研究，最终实现激光陀螺仪的机械抖动控制技术，表达式为：

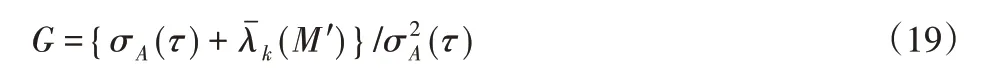
3 实验结果与分析

实验过程中采用内存为5GB 的计算机，计算机的系统为WindowsXP，在光学转台上，通过方差分析法的激光陀螺仪机械抖动控制技术进行实验。

3.1 机械抖动信号输出频率测试

利用激光陀螺仪的脉冲当量和输出信号分析激光陀螺仪的机械抖动信号输出频率测试，如表1所示。

表1 激光陀螺仪的抖动信号输出Tab.1 Jitter Signal Output of Laser Gyroscope

图3 机械抖动信号输出结果Fig.3 Output Result of Mechanical Jitter Signal

正常状态下，信号的机械抖动频率为318Hz。在文献［2］控制下，除谐振频率外，出现629.1Hz、943.6Hz、1258Hz、1573Hz、1887Hz、2202Hz 等频率成分。文献［3］控制后，谐振频率几乎消失，但出现干扰频率572.2Hz，而这里方法的机械抖动频率最接近原始信号频率，说明这里方法在控制输出信号还原度方面较强，能够准确输出信号。

3.2 激光陀螺仪信号的稳定性测试

为了测试激光陀螺仪信号在控制信号方面的稳定性，设定具体的原始信号，在不同的时间下测试将这里方法与文献［2］、文献［3］方法的频率幅值，将测试结果进行对比，对比结果，如图4所示。

图4 激光陀螺仪信号的稳定性测试结果Fig.4 Tability Test Results of Laser Gyro Signal

由图4可知，在进行激光陀螺仪信号的稳定性测试时，原始信号的频率幅值波动较大且不稳定，在文献［2］方法的控制下，输出原始信号后的波动幅值范围减少但频率幅值波动不大；文献［3］方法控制下的部分信号幅值波动频率减小，但整体波动范围没有较大改变；而这里方法控制下的信号频率幅值相对来说波动较小且范围减少，说明这里方法控制下的信号在输入与输出过程中受到机械抖动的干扰较小，信号较为稳定。

3.3 激光陀螺仪机械振动频率控制可靠性测试

不同方法的机械振动频率控制可以得出不同的信号输出效果，为了验证这里方法的输出信号的可靠性，进行实际输出与期望输出的对比测试，测试结果如下图所示，其中，一部分表示期望输出，另一部分表示实际输出。

由图5可知，在进行实际输出与期望输出的对比时，输入原始信号频率的实际输出与期望输出差别较大，在文献［2］、文献［3］方法的控制下，实际输出皆在不同程度上吻合期望输出，但仍有部分训练样本数据吻合失败，而在这里方法的控制下，大部分的实际输出样本序列与期望输出相吻合，表明这里方法有较强的机械振动频率控制可靠性。

图5 实际输出与期望输出的对比图Fig.5 Comparison Between Actual Output and Expected Output

减少抖动噪声可以使控制系统直观的反映激光陀螺仪机械抖动的好坏，并根据激光陀螺仪的稳定性和工作可靠性判断激光陀螺仪的性能，综上所述，应用这里方法可以影响陀螺仪的抖动情况，使激光陀螺仪具有减少抖动噪声、输出信号稳定性较好和工作可靠性较高的优点，提高激光陀螺仪的工作效率。

4 结论

这里主要提出一种基于方差分析法的激光陀螺仪的机械抖动控制技术，其主要通过激光陀螺仪的机械抖动方程分析激光陀螺仪的正弦抖动信号，利用laplace的变换和反变换计算分析激光陀螺仪机械抖动控制的电路，引入方差分析法得出激光陀螺仪的抖动时间，分离激光陀螺仪中的误差源，最后实现激光陀螺仪的机械抖动控制技术，并在测试实验中利用激光陀螺仪的脉冲当量和输出信号分析激光陀螺仪的机械抖动信号输出频率，应用激光陀螺仪的机械抖动频率和实际输出与期望输出吻合程度进行对比测试，测试结果表明这里方法缓解了激光陀螺仪噪声多、稳定性差和工作可靠性差的问题，实现了激光陀螺仪机械抖动控制技术，为实现激光陀螺仪的整体数字化奠定基础。