一种改进的疏散节点踩踏风险评估算法*
2022-05-19王保云
王保云,王 婷
(1.云南师范大学 数学学院,云南 昆明 650500; 2.云南师范大学 外国语学院,云南 昆明 650500)
0 引言
随着人类社会的发展,各类大型活动不断增加,人群聚集场所的拥挤踩踏事件也不断增加。拥挤踩踏事故会造成大量人员伤亡,给社会造成恶劣影响,并引发一系列公共安全问题。在大型活动的防踩踏安全预案制定中,除预估人流疏散效率与控制人群密度外,事先评估场所疏散节点的固有风险尤为重要。针对活动场所的踩踏风险问题,许多学者从不同方面开展研究:刘晓芳等[1]、Wieringa[2]、Lian等[3]研究街道、广场、公园等室外大型社会活动场所的踩踏事故形成机理;刘莉媛[4]针对体育赛场进行踩踏事故的风险评估;徐海秋[5]分析台阶路段的行人交通行为;刘艳等[6]构建了地铁车站的踩踏事故风险评价模型;李成龙等[7]对不同形状出口的拥挤情况进行探讨;Alonsomarroquin等[8]对走廊通道的行人动力进行模拟。上述研究多针对不同场所的踩踏事件形成机理和行为模型等,很少涉及场所在疏散过程中的节点风险评估问题。针对这一现状,乔来明[9]通过分析安全设施与数量、安全通道数目和方位等方面构建体育赛场的风险评估体系;文献[10-11]提出基于最小宽度系数、倾斜度、汇集度和长度的四变量场所风险评估算法。
四变量算法一定程度上解决了疏散节点(Evacuation Node,EN)和场所的风险定量计算问题,但由于存在宽度系数和倾斜度采用分段函数、汇集度依赖于疏散面积而不是人流股数等问题,使得算法的准确性和应用范围都受到很大限制。本文通过重新构造倾斜度函数、宽度系数函数、汇集度函数,进而提出新的踩踏风险模型,以评估公共场所中EN的踩踏风险,达到提升算法稳定性和敏感性的目的。
1 四变量评估算法及存在的问题
1.1 四变量算法
在四变量算法中,根据节点特性及其在疏散过程中起到的作用,分为点型节点(Point-type Node,PN)、线型节点(Linear-type Node,LN)和面型节点(Surface-type Node,SN)。PN指长度值、倾斜度值较为固定且汇集度值较高的一类节点,例如出入口;LN指在人群疏散时具有线段形状的风险区域,例如过道、隧道等;SN指台阶、坡面等面状疏散区域。
倾斜度、最小宽度系数、汇集度和长度是四变量算法的基本变量。通过对4个基本变量进行建模,计算EN和场所的踩踏风险。
对于楼梯等坡度较大的LN,倾斜度函数[10]如式(1)所示:
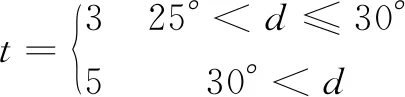
(1)
式中:t为倾斜度;d为坡度,(°) 。
对于以台阶为代表的LN或SN,倾斜度值定义为2,3,4,对应坡度范围分别为d≤15°,15° 依据单股人流宽度和双股人流的通行情况,应用式(2)计算宽度系数[10]: (2) 式中:b为宽度系数;u为EN宽度,m。 汇集度函数定义如式(3)所示: (3) 式中:c为汇集度;s为EN承担的疏散面积,m2;w为EN的有效宽度,m。 EN风险评估算法如式(4)所示[10]: r=b+α(c,l)t (4) 式中:l为EN的长度,m;α(c,l)为汇集度c和长度l的函数。对于PN,αPN(c,l)=cl;如果节点为LN,则有αLN(c,l)=c+l0.5;对于SN节点,有αSN(c,l)=c+l。 1)分段函数带来的稳定性和敏感性问题。关于稳定性,由于宽度系数和倾斜度均采用分段函数,导致计算结果在断点附近稳定性差,宽度或坡度发生很小的变化,结果改变较大。而分段函数每一段内的宽度和倾斜度均取常数,使分段区间内的宽度系数和倾斜度不能反映相关参数的变化,敏感度较差。 2)宽度系数与人流股数的问题。当通道宽度为0.55~0.6 m时,才允许单股人流通过[12-13]。由于人体肩宽为0.4 m[14],可认为小于此宽度的通道无法通过行人。式(2)虽然考虑1股人流的通过和2股人流的碰撞问题,但没有考虑宽度小于0.4 m时的不可通行问题。同时,在很多公园和广场的楼梯、台阶和坡面的宽度各不相同,且远大于1.4 m,宽度系数均归一化为1显然是不合理的。 3)汇集度只考虑疏散面积而未考虑人流的股数问题。汇集度只与直接相连接的节点或区域有关,而与距离更远的节点或区域无关。不同类型的疏散节点如图1所示。其中,图1(a)为高度为1层的厂房,共4个房间R1,R2,R3,R4,房间门分别为D1,D2,D3,D4;房间疏散门通过过道C1,C2与厂房大门D5相连;与D5直接相连的疏散节点为D2,D3,C1,C2,而D1和D4需要通过C1,C2才能到达疏散节点D5,所以D5承接的人流量由D2,D3,C1,C2决定,按式(3)将用4个房间的面积计算,并不合理。在图1(b)中,楼梯S2承接的人流来自上一层的楼梯S1和与之相连接的过道C3,C4。广场、公园、学校中与台阶或通道直接相连的大门仅承担1个EN的人流汇合,如图1(c)所示,这种情况下只需考虑与D6所连接的台阶S3的人流量。 图1 不同类型的疏散节点 4)评估算法的无效参数问题。对于PN而言,长度等同为墙的厚度,取值较为恒定,一般也不存在节点太长而引起人群拥堵的情况。同时,PN节点不存在倾斜度问题。因此,rPN的表达式中,l和t并不是变量。在式(4)中,宽度系数和汇集度的作用较为重复,需要进行区分。 1)楼梯倾斜度性质分析 楼梯和过道均为狭长的LN,可以通过分析2者的危险程度对倾斜度进行建模。统计可知,发生在楼梯和过道的踩踏事件比为63∶14=4.5∶1[10]。 一般楼梯的坡度范围为25°~45°,建筑内楼梯坡度的最佳坡度为30°[15-16]。因为过道为0°,可认为在其它条件不变时,坡度为30°的楼梯的危险性是坡度为0°的过道的4.5倍。考虑统计数据的误差,将倍数放宽为4.0~5.0倍较为合理。 2)楼梯倾斜度函数 通过上述分析可知,楼梯倾斜度函数建模如式(5)所示: t=ft(θ) 25°≤θ≤45° (5) 函数需满足以下倾斜性质(Tilt Property,TP): TP1:当θ=30°时,4.0≤ft(30°)≤5.0。 根据上述要求,构建函数如式(6)所示: (6) 式中:C1和C2为常系数,一般取C1=1.1,C2=0。则有式(7): (7) 可验证ft(30°)=4.4,则有式(8): (8) 在定义域上满足f′(θ)>0。需要说明的是,式(6)并非是满足TP1和TP2的唯一函数,其它满足倾斜性质的函数亦可用于度量楼梯的倾斜度。 3)坡道和台阶的倾斜度函数 台阶的坡度一般为14°~27°,而斜坡路面的最大纵坡降常为1.7°~12°。王保云等[10]认为楼梯的危险性相对最高,台阶次之,而坡道和坡面相对最低。坡度度数与危险性成正比依然成立。因此,对于台阶、坡道和坡面,可以将式(7)的定义域直接扩展为0°<θ≤45°。扩展定义域后得函数仍然满足TP1和TP2。 1)宽度系数性质分析 虽然很多宏观模型将人群疏散类比于液体流动,但人群并非完全的流体。由于人群是由独立的个体组成的,所以具有明显的离散性。人群的离散性还表现为:设宽度为w时,刚好允许单股人流通过,则宽度为nw可以通过n股人流;当宽度为1.5w时,通道宽度的增加使单股人流的通行效率增加,可以认为稍大于1股人流,但并非是1.5股人流。 2)宽度系数函数 人流股数与通道宽度的关系函数如式(9)所示: b=fb(w) (9) 式中:b为以人流股数为单位的宽度系数,股;w为EN宽度,m。 设W1为人体肩宽,W1称为截止宽度,即当宽度小于W1时,人流是不允许通过的;设W2为单股人流宽度,W2称为通行宽度,即当宽度大于W2时,人流疏散较为通常。据此分析,得到宽度系数函数需要满足的4条性质(Width Property,WP): WP1:当0≤w WP2:当w=nW2时,fb(w)=n。 WP3:当w=nW2+0.5时,n≤fb(w) WP4:设ε≥0为1个很小的数,则w=nW2±ε时,fb(w)≈n。 据此,构建函数如式(10)所示: (10) 0≤k1(0.5)k2<0.5 (11) 结合WP1和WP4,当w=W1 (12) 由式(12)可得k1>0和k2>>1。k1为该项的调节系数,为计算简便,可取k1=1。 图2 不同幂次函数的宽度系数 (13) 宽度函数示意如图3所示。其中,实线表示式(13)拟合得到的宽度系数与宽度关系,这里的宽度系数与四变量法中宽度系数定义略有区别。四变量法是以建筑火灾疏散中单股人流能否疏散、2股人流是否碰撞为依据来确定宽度系数,宽度值越大,宽度系数越小。对宽度大于2股人流宽度时,宽度系数均设为1。本文算法综合考虑人流股数对疏散的影响和宽度系数的平滑性,定义如式(13)所示的宽度系数函数,宽度值越大,宽度系数越大。 图3 宽度函数示意 由图3可知,在宽度为0.5~1.4 m时,2个算法都能按人流股数来度量宽度。但相比四变量算法的分段函数,本文算法的平滑性更好,并且在宽度大于1.4 m时,仍以股为单位计算宽度系数,显然更为合理。 1)汇集度性质分析 根据《建筑设计防火规范》(GB 50016—2014(2018年版))规定,对于一二级耐火等级的建筑,每个疏散门的疏散能力为80人/股。因此对于直接与疏散区域相接的疏散节点,汇集度可以用其承担的疏散人数计算,如式(14)所示: (14) 式中:c为汇集度;p为待疏散人数,人;γ为疏散系数,80人/股。当EN与人群聚集区域直接相连且承担疏散功能时,式(14)计算得到的汇集度比较合理,比如房间门、与广场直接相连的大门、台阶、通道等。但在EN之间前后相连时,从疏散顺序来说,排在后面的EN的汇集效果只与其前面相连的EN有关,而与距离更远的人群聚集区域无关。 实际情况中,待疏散人数是未知的,因此需要考虑在疏散方向上的前驱节点和区域。通过对前驱节点和区域的最大人流股数,来预测当前节点所要承担的疏散压力,即该节点的人流汇集程度。 2)汇集度函数 通过前面的分析可知,对于汇集度的建模需要构建函数如式(15)所示: (15) 函数满足以下汇集性质(Convergence Property,CP): CP1:按疏散人流方向,应考虑所有与之相连的EN的人流量。 CP2:汇集强度应以人流股数的倍数来衡量。 通过上述分析,汇集度计算如式(16)所示: (16) 式中:bi为第i个前驱节点的宽度系数;b为当前EN的宽度系数;N表示前驱节点的数目。根据式(9)可进一步得到式(17): (17) 式中:wi为第i个前驱节点的宽度;w为当前EN的宽度。 EN的踩踏风险由其拥挤概率来决定。如果不会发生人群拥挤,自然也就不会在该节点处发生踩踏。经常发生人群拥挤的EN,必然是人群踩踏的高风险节点。对于以疏散门为代表的PN,节点的长度与墙的厚度保持一致,可看作为恒定值,并且也不存在倾斜,因此可忽略倾斜度和长度的影响。当所承担的疏散荷载超过其所能通过的人流股数时,就会发生拥挤。可以看出,在该节点处发生拥挤的概率直接由汇集度决定。因此,PN的踩踏风险如式(18)所示: rPN=c (18) 同样地,对于以楼梯为代表的LN来说,拥挤度和倾斜度是评估踩踏风险的最关键因素,2者为乘积关系[10]。长度也会影响风险值,长度越长,该节点滞留的人数越多,越容易造成拥挤踩踏。根据上述分析,可用式(19)计算LN的踩踏风险: rLN=ct+l0.5 (19) 式中:l表示节点长度。 台阶、坡面等SN的拥挤发生概率的分析与LN类似,仍可用式(19)进行计算。 为验证算法的有效性,设计以下3个关于疏散节点的踩踏风险计算例子: 1)例1:在图1(a)中,4个房间R1~R4的面积均为1 000 m2,每个房间工作人员为56人。各EN参数为:墙的厚度为0.37 m,疏散门D1~D4宽度为1.2 m,过道C1的长宽和C2相同,分别为10 m和1.3 m,大门D5宽度为1.4 m。计算D5的踩踏风险。 2)例2:在图1(b)中,各EN参数为:S1的长宽和S2相同,分别为3,1.6 m,2段楼梯与水平面的夹角均为30°;过道C3的长宽和C4相同,分别为6,1.4 m;每层楼有4个教室,总面积为240 m2。计算S2的踩踏风险。 3)例3:在图1(c)中,各EN参数为:台阶S3的长度和宽度分别为15,8 m,纵坡降为15°,所连接的疏散区域为2 000 m2,人员密度为1人/m2;大门D6的宽度为3.6 m。计算S3和大门D6的踩踏风险。 各EN的踩踏风险计算见表1。由表1可知,楼梯S2的风险最高,台阶S3次之,2道大门D5和D6的风险较低,与实际情况较为符合。 表1 各EN踩踏风险 为进一步验证算法的性能,设计如下实验,计算在不同情况下的踩踏风险值变化情况,并与四变量法做比较。 1)(E1)在例1中,D5的宽度从0.3 m增加至3.0 m,分析D5的危险度变化情况。主要是考察PN类节点随宽度的变化趋势,以及在宽度小于截止宽度时风险值是否合理,结果如图4(a)所示。 2)(E2)在例2中,S2的坡度从20°增加到45°,分析S2的危险度变化情况。可以看出LN类节点风险值与坡度之间的稳定性和敏感性问题,结果如图4(b)所示。 3)(E3)在例2中,S2的宽度从1.0 m增加到2.8 m,分析S2的危险度变化情况。该例用于考察LN类节点风险值随宽度的变化情况,并验证宽度系数是否按人流股数来度量,结果如图4(c)所示。 4)(E4)在例3中,S3的坡度从10°增加到30°,分析S3的危险度变化情况。考察SN类节点风险与坡度的变化规律,验证此类节点风险值在坡度参数影响下的稳定性和敏感性问题,结果如图4(d)所示。 5)(E5)在例3中,S3的宽度从3.6 m增加到12.0 m,分析D6的危险度变化情况。考察公园类宽度值较大的大门类PN风险值与宽度的关系,结果如图4(e)所示。 PN类节点处是否发生拥挤,主要受2个方面的影响:一是本身宽度值大小,二是与其相连接的节点宽度值大小(代表了汇集程度)。图4(a)中2个算法都显示该类节点的风险与自身宽度成反比,与实际相符,但四变量法缺乏对极窄节点的识别。当节点宽度小于0.4 m(单人肩宽)时,该节点因为无法使人流通行而风险无限增高。当与其相连接的节点宽度(之和)较大时,表明汇集到该节点的人流股数较多,风险应该升高。图4(e)中,四变量法显示D6的风险与S3的宽度无关,这是因为应用四变量法计算D6的风险时,只需要考虑其所承担的疏散面积,而不用考虑S3的宽度,这显然是不合理的。因为当S3宽度较小时,人群的拥挤更可能发生在S3而不是D6,即S3的踩踏风险升高而D6降低。在这一点上,本文算法也明显优于四变量法。 图4 算法性能比较 在图4(b)中可以看出,受分段函数的影响,四变量法在坡度为30°时有很大的阶跃,在该点之前和之后,坡度的变化不会引起风险的变化;而在阶跃点,只要坡度发生很微小变动,都会引起风险的急剧变化。显然四变量法在度量LN类节点与坡度的关系时并不稳定,本文算法则可以很好避免这一问题。由图4(c)可知,随宽度增加,风险在逐渐减小,四变量算法和本文算法均准确地体现了这一趋势,但正如WP1~WP4所揭示的性质规律,风险与宽度并非是完全光滑的函数关系,宽度值所描述的人流通行能力需要折算为人流股数来计算。从这一点来说,本文算法强于四变量法。 从图4(d)可以看出,风险随坡度的增加而增加,但由于四变量法采用分段函数,导致风险在15°和27°处发生很大的变化。本文算法由于构造连续的函数来刻画坡度与风险之间的关系,可以避免这种不合理的阶跃。 1)四变量算法在踩踏风险评估时存在的问题包括分段函数带来的稳定性和敏感性问题、人流股数在宽度系数计算中的度量问题、前驱节点疏散能力与汇集度之间的关系以及风险评估算法的无效参数问题。 2)通过改进倾斜度模型、宽度系数模型、汇集度模型,据此提出更为简洁的踩踏风险评估算法。通过实例验证,对于点型节点、线型节点和面型节点,改进算法在危险度数值的合理性和算法稳定性上表现更为优异。 3)踩踏事故的发生,除场所自身因素外,还存在人流疏散路径安排是否合理、活动的安全管理是否到位等因素。本文算法中的EN风险评估,是衡量静态的、独立于人群的,如何将场所中EN风险与人群疏散过程相关联,更准确地评估人群拥挤程度和避免踩踏事故的发生,是下一步重点研究内容。
1.2 存在的问题

2 改进的EN踩踏风险评估算法
2.1 倾斜度模型
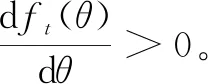
2.2 宽度系数模型

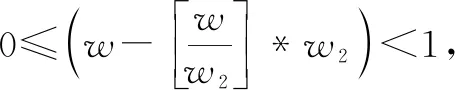


2.3 汇集度模型
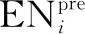
2.4 EN踩踏风险模型
3 实例与讨论
3.1 EN踩踏风险计算

3.2 算法性能分析

4 结论
