三通管不同开口状态下爆炸气流湍流变化规律*
2022-05-19王开民毕海普雷伟刚
王开民,毕海普,雷伟刚,邵 辉
(常州大学 环境与安全工程学院,江苏 常州 213164)
0 引言
可燃气输运管道系统错综复杂,三通型管作为特殊管型,燃爆发生后,爆炸气流湍流、火焰传播、爆炸压力等参数之间存在复杂的耦合规律,而基于管型的爆炸湍流变化及流场分布是三通管中爆炸火焰传播、压力动态变化等的基础核心因素,因此爆炸湍流规律的研究对爆炸风险防控及管道优化布局具有重要意义。国内外专家学者们对三通管内预混可燃气爆炸气流及湍流的传播特性进行了一定研究,2005年,翟成等[1]对分支管路内可燃气爆炸的湍流生成及火焰传播规律开展了研究,通过试验得出分岔处诱导附加湍流,使火焰加速,为后续研究奠定了基础。林柏泉等[2]在通过分岔管道爆炸实验,在翟成的基础上进一步分析了分岔处湍流的作用,阐明了湍流对火焰及冲击波增强的机理。Zhang等[3]通过实验揭示了分支隧道对油气混合气爆炸超压、超压上升速率、严重因子和燃烧速度的影响。文献[4-5]对T型管道内的油气爆炸进行研究,指出导致T型分支管道内爆炸压力增强的主要因素,包括波的绕射和反射,管道面积突扩和障碍物扰动以及流场湍流增强。耿进军等[6]发现单向分岔管道分流系数随初始超压的增大而增大,随分岔角度的增加而增大。Zhu等[7]和Lin等[8]通过对称和非对称分支管道内的爆炸实验,分析了火焰速度的变化规律,并建议使用纹影装置及数值模拟进行进一步的实验研究。Emami等[9]实验发现,点火点与障碍物之间距离较短的情况下,三通效应引起的横向压力波与火焰有较强的相互作用。Li等[10]实验研究发现,随着三通支管数量的增加,湍流强度的增大使得管内压力上升速率也明显增加。李蒙等[11]研究发现,在半开口管道工况下,由于泄流现象及开口处扰动,湍流强度增大会导致管外火焰翻转拉伸形成蘑菇云状。周宁等[12]通过数值模拟,得出涡团及涡对的运动,对火焰阵面变化有重大影响。刘冲等[13]在双分支管道内研究火焰传播及流场变化情况,结果表明分支管道内已存在的流场影响了火焰传播,导致火焰锋面褶皱变形,呈现浪花状。
目前国内外对分支管道内可燃预混气爆炸的研究主要集中于爆炸超压及火焰传播规律的研究,对湍流动能变化、流场分布及与火焰的耦合规律研究较少。鉴于此,通过构建数值模拟闭口和开口三通管道模型,分析爆炸湍流动能及流场变化,以期为工业复杂管道发生爆炸后的火焰及压力传播规律的研究提供理论支撑。
1 气体爆炸管道模型建立
本文管道模型是基于可燃气体运输管道特点而分析和设计。
1.1 数学方程
数值模拟采用计算流体力学软件FLACS中的气体爆炸模块,数学模型所包括的基本方程有:质量、动量方程及能量3大守恒方程、燃料组分方程和混合物组分方程,将各方程耦合后,如式(1)所示[14]:
(1)
式中:ρ为密度,kg/m3;t表示时间坐标,s;x表示空间坐标;ui为xi方向上的速度,m/s;φ为通用变量;Sφ为能量源项,无量纲;μeff为有效黏性;σφ为普朗特常数,无量纲。
湍流模型对标准k-ε方程进行修正,湍流动能及湍流动能的耗散方程定义,如式(2)~(3)所示[14]:
(2)
(3)
式中:k为湍流动能,m2/s2;ε为湍流动能耗散率,m2/s3;C1、C2、σk、σε为模型常数,分别取值1.44、1.92、1.3、1.0;G为湍动能的产生项。
预混气体的燃烧过程采用耦合复杂化学反应的涡耗散概念(EDC)燃烧模型计算,其反应速率表达式,如式(4)所示[14]:
(4)
式中:ωi为反应速率;γ是细微结构中反应物的质量分数;χ为细微结构反应分数,χ=1;τ*是细微结构的特征时间尺度;Yi0为反应器外组分i的质量分数;Yi*是密度加权的组分质量分数。
使用光学薄气体体积辐射热损失模型,高度简化处理辐射热损失,该模型计算燃烧气体到外壳壁上和未燃烧气体体积的辐射热损失。
结合上述基本方程,软件采用有限体积法在三维笛卡尔网格条件下来求解可压N-S方程,来计算三维模型下气体火灾或者爆炸,进而得到相关爆炸参数数据。
1.2 模型构建
根据工业管道特点,设置管道内径0.125 m的密闭三通管,水平管道长度为7.8 m,分叉管长度2.2 m(垂直于水平管道)。为简化描述,将管道分为A,B,C3段,其中管道A长为5.6 m,垂直岔管B和水平岔管C的管道长均为2.2 m。管道前端2.1 m处设置有爆破片,类型为Popout的泄爆膜,泄爆膜功能与实验状态接近。为了使数值模拟与工业实际更接近,设置管道的热交换,使爆炸过程中的能量传播到环境中。数值模拟中监测点设置与实验中相对应,初始参数如下:丙烷/空气预混气浓度为3.9% v/v,环境温度为20 ℃,初始压力为0.1 MPa,边界条件为Euler边界,未设置初始湍流。
为保证模拟的精确度及运算速度,整个计算区域采用均匀网格划分,网格密度为0.012 m,计算区域中X,Y和Z轴上的网格数分别为986,243,20。管道数值模型与网格划分,如图1所示。

图1 管道数值模型与网格划分
1.3 模型验证
本文实验管道基于工业管道特征和数值模拟管道模型搭建,该装置平台主要由5大系统构成:数采系统、点火系统、配气系统、管道系统以及各类辅助设施组成,实验数据用于验证数值模拟的准确性。实验管道为内径0.125 m的密闭三通管,水平管道长度为7.8 m,分支管道位于水平管道5.6 m处,长度为2.2 m(垂直于水平管道),如图2所示。数据采集系统包括火焰传感器、压力传感器、TST3406数据采集处理系统。压力传感器型号为CY400,测量爆炸超压。火焰传感器型号为CKG100,其可以将微弱的光信号转换为电信号。点火系统(型号EPT-6)设置在管道左侧端口,可产生18 J燃烧火花。本文以丙烷气体作为实验介质,丙烷/空气预混气浓度为3.9% v/v,在混合气体容器中采用分压法制备。测试数据取3次重复实验的平均值。

1.爆破片;2.可视窗口;3.高速摄影仪;4.数据采集器;5.点火系统;6.点火电极;7.电脑;P1~P5压力传感器;S1~S6光电传感器;M为湍流动能监测点
实验测试和数值模拟管道内丙烷爆炸传播结果对比,如图3所示。

图3 实验测试和数值模拟数据比较
三通管中的P3处压力传感器压力曲线对比图如图3(a)所示,该点数值模拟和实验的压力随时间变化趋势基本相同。由图3(b)可知,实验所得的最大爆炸压力与模拟数值相比差值最高不超过0.018 4 MPa,相对误差小于10.38%。
综上所述,数值模拟与实验数据吻合较好,各点压力变化趋势基本一致。鉴于此,数值模拟管道模型具有较好的合理性和较高的准确性。
2 不同开口状态下爆炸气流湍流变化规律
当丙烷-空气预混气体在三通管中爆炸后,爆炸气流(未燃气体及燃烧产物)在管道内进行传播,受到爆炸冲击波、火焰、障碍物的影响,爆炸气流的传播方向及速度梯度发生变化,形成湍流,进而与燃烧过程形成反馈机制。本文通过设置不同开口状态,分析三通管中爆炸湍流的变化规律。
2.1 爆炸湍流动能峰值变化规律
湍流动能随时间的变化体现湍流动能的净收支,是衡量湍流发展或衰退的指标。不同工况下湍流动能k的峰值随距离的变化曲线见图4。
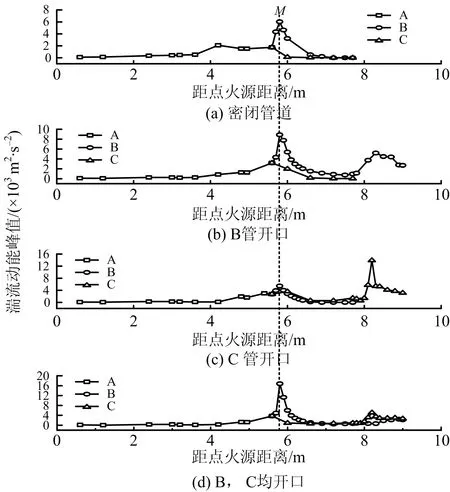
图4 湍流动能峰值随距离变化
图4中,图4(a)为密闭管道,图4(b)为B管开口,图4(c)为C管开口,图4(d)为B、C管道均开口的情况。图4中湍流动能峰值随距离的变化规律显示,4种工况下,湍流动能在A管道前3.6 m数值变化较小。当爆炸气流继续向前传播,垂直支管5.8 m处(图2中M点)出现了首个湍流动能峰值,4种工况下,最大峰值均显示在垂直岔管B中;随着气流传播继续进行,涡旋能量衰减,大尺度涡旋向小尺度涡旋演化,管内的湍流动能持续衰减。
开口状态对湍流峰值最大值的影响显示,当爆炸气流传播至管道外侧,失去管壁约束,能量迅速向空中释放,气流速度增大,湍流动能增强。不同开口状态下最大湍流动能峰值,如表1所示。

表1 各工况最大湍流动能峰值
综合以上数据,各工况下,管道内部湍流主要集中在垂直支管B内,相较于密闭管道,垂直管道B开口,B管内湍流动能增大了29.86%,C管内增大了82.76%;C管开口,B管内湍流动能下降了10.12%,C管内增大了107.39%。B,C均开口,B管内湍流动能增加了178.45%,C管内增加了114.12%。
对于管道外侧的湍动能情况,单侧管道开口,C开口比B开口,管外湍流动能峰值高出167.91%;B,C均开口,C管外侧也比B管外侧高出135.15%。因此,湍流更易在水平C管外侧发展,B管外湍动能相对较小。
2.2 管内爆炸气流湍流分布规律
湍流动能k越大表明湍流脉动长度越大。在多尺度湍流模型中,湍流由各类尺度涡动结构共同组成,大型湍流携带并向其传递能量,小型湍流则将这些能量全部耗散作为内能。在一般的情况下,涡旋的能量总是从大尺度的涡旋到小尺度的涡旋进行传递。在逐级传递的过程中,外部环境条件的作用使其受到逐步减弱或衰退,逐步丧失了大尺度的涡旋各向异性的特征,而更加倾向于小尺度的涡旋各向异性。[15]
爆炸初期,冲击波及火焰推动已燃气体及部分未燃气体向前传播,气流流速慢,湍流仅出现在火焰阵面附近且湍流度较低;而随着管道分支,当爆炸气流在经过楔形扰动源s后,在B管左侧形成膨胀波,气流流经该区域,会导致压力、温度等状态参数下降,因此s点是1个会不断产生负压的扰动源,与此同时气流速度会得到提升,如图5(a)所示,圈内为低压区域,气流流经此处发生偏转,形成湍流旋涡;爆炸前驱压力波速度总小于后产生的压力波,而当强压力波推动速度更高的气流传至分岔处,低压区面积随之增大,B管右侧气流经过加速速度明显高于C管,而B管右侧壁面作为边界,规定气流流向,因此气流沿右侧壁面传入支管中,受到左侧负压区域的吸引及加速后,爆炸气流湍流动能增大,湍流面积扩大,并不断向前方发展,如图5所示。

图5 分岔处湍流变化
对于湍流的后续发展,在不同开口工况下,由于封闭端反射压缩波波及火焰传播情况的不同,湍流的传播情况各不相同,图6为同一时刻54 ms各工况下火焰传播情况。在密闭工况下,由于B,C管端均封闭,产生的反射波逆向传播,而C管中反射压力波传播更快,到达分岔处,与A管内正向压力波碰撞叠加向B管内传播,火焰经过分岔处时受湍流拖拽,火焰阵面扭曲并向B管内传播,但由于B管内存在反射压力波,因此气流在向前传播过程中,速度急剧减小,湍流无法持续发展,如图6(a)所示。当B端开口后,C管中的反射压力波与正向传播的压力波存在竞争关系,阻碍了一部分正向气流的传播,同时导致了连续火焰的断裂,如图6(b)所示,但由于B管1侧开口,C管内更多反射压力波传向支管内,提升了气流速度,因此该工况下湍流尺度更大,湍流动能增大了29.86%。针对于C开口的工况,B管内的反射压力波阻碍了分岔处气流向B管内传播,形成湍流旋涡的气流速度迅速下降,并且方向逆转,阻碍了火焰向B管内传播,如图6(c)所示,B管内气流与A管内气流一起向C管中传播,加快了火焰在C管内的传播速度,因此C开口情况下,B管内湍流动能峰值下降了10.12%,但C管外侧相较于B开口情况下B管外侧湍流动能高167.91%。B,C均开口的情况下,无反射压力波的阻碍,火焰更快进入B管中,此时B管中的爆炸气流携带未燃气体形成的湍流漩涡被点燃,使燃爆反应速度加快,火焰的燃烧面积增加,而反应速度增加,又对湍流起到了增强作用,进而形成燃爆反应与气体流动间正反馈机制,而正向冲击波推动气流,对火焰及湍流传播起到加速作用,因此B,C开口工况下,管内湍流动能峰值相较密闭管道增加了178.45%,但由于管内大尺度湍涡消耗了更多能量,因此管外湍动能数值较低。

图6 分岔处火焰传播
2.3 管外爆炸气流湍流分布规律
当爆炸气流传播至管道外侧后,由于失去了管道的束缚,湍流动能随之增大,气流向四周扩散,3个开口工况下,湍流动能均呈现先增后减的趋势。对比3种工况,由于惯性作用,爆炸气流更易在水平管道中传播,C管外的湍流动能高于B管外侧。而B,C开口工况下,由于湍流与火焰的正反馈机制,使湍流动能增大,形成大尺度湍流,促进了火焰的传播,同时消耗了更多能量,因此管外的湍流动能相较2个单开口的数值更小。
管道外侧湍流发展,如图7所示。以B管外侧为例,爆炸气流呈现以管轴中心处气流速度最高,并向四周递减的传播情况,气流不受到管壁限制,具有向管道四周流动的倾向,如图7(a)所示;高速气流进入相对静止的管道外侧大气时,管外流场发生紊乱,各方向压力梯度与密度梯度相交,形成斜压效应。促使爆炸气流形成涡旋,涡旋拉伸效应会推动爆炸气流持续进行横向扩散。与此同时爆炸引起的压力上升小于泄放引起的压力下降,管口处形成的小面积负压区域,导致爆炸气流向两侧偏移后又向管轴中心聚拢,因此管口处及轴线两侧湍流动能较高,湍流漩涡的发展更快,如7(b)所示;随着气流速度的增大,推动外部流场区域形成双涡旋结构,管轴中心线右侧涡旋为顺时针,左侧涡旋为逆时针,湍流动能逐渐增大,形成剑柄状的多尺度湍流动能场;60~62 ms,爆炸火焰从管道右侧传出,增强了右侧的湍动能,同时湍流发展,漩涡范围更大,如图7(d)~7(e)所示;最后气流向周围扩散,湍动能逐渐降低。

图7 B管道外侧湍流变化
3 结论
1)不同开口状态下,管道内湍流动能峰值最大值均出现在垂直岔管B内。相较于密闭管道,垂直管道B开口,管内最大湍流动能峰值增大了29.86%;C管开口,峰值下降了10.12%;B,C均开口,峰值增大了178.45%。对于管道外侧的湍动能情况,单侧管道开口,C开口管外湍流动能峰值比B开口高出167.91%;B,C均开口,C管外侧也比B管外侧高出135.15%。因此,开口情况下,湍流更易在水平管道外侧发展。
2)对于管道内部的湍流发展,与湍流同向的冲击波,会增加气流速度,增大湍流动能,从而对爆炸火焰起到更强的拖拽作用,使火焰阵面更易接触爆炸气流携带未燃气体形成的湍流漩涡,使燃爆反应速度加快,火焰的燃烧面积增加,因而反应速度增加,对湍流起到了增强作用,进而形成燃爆反应与气体流动间正反馈机制。而逆向冲击波则会阻碍湍流的发展。
3)爆炸气流传播至管道外侧后,由于失去了管道的束缚,湍流动能随之增大,管道外侧爆炸气流形成以管轴中线气流速度最高,并向四周递减的传播情况,管道端口处形成双涡旋结构湍流。3个开口工况下,管外湍流动能均呈现先增后减的趋势。
