哈密顿光学理论在变折射率问题中的应用*

方润根 张舒程 陈 诺(杭州学军中学 浙江 杭州 310012)

在近两年全国中学生物理竞赛复赛试题中，36届的阶跃型光纤耦合问题以及37届的光纤陀螺仪模型都涉及到了阶跃型光纤的光路问题，而在实际光纤通信中，一般使用具有较高数值孔径的渐变型光纤进行通信，使光具有强汇聚效果与较小的畸变.分析变折射率光纤中光传播路径是很有必要的.由理论力学的分析思路出发[1]，利用哈密顿原理由欧拉方程出发建立了哈密顿光学理论，最后得到哈密顿正则方程来求解光线在变折射率介质中的轨迹方程，作为现代光纤通信的基础.但是对于高中物理竞赛学生而言无疑要求过高，本文由哈密顿光学理论出发，用一种规避复杂数学运算的方式去类比粒子在势场中的运动轨迹，并通过几个模型更加直观地理解并使用该方法解决变折射率光纤中的光传输问题.

哈密顿在早年发现理论力学的分析方法可以迁移到几何光学中，费马原理与哈密顿原理惊人的相似[2].哈密顿原理具有高度的概括性，作为物理学的最高原理，不论怎样的物理系统，只要确定其拉格朗日函数，就可用哈密顿原理来推导其运动方程[3].具体的数学处理过程可参照理论力学教材及相关文献[1,4].

1 高中阶段的类比理解与解题策略

本文采用类比的方法将光线在径向变折射率介质n(r)中的传播轨迹看作是实物粒子在有势场中的运动轨迹.

其中左式积分代表光传播的路径是光程取极值的路径，右式是莫培督原理的表达式，通过对坐标函数的作用量采用最小作用量原理，对一个不显含时间t的系统，通过能量守恒将作用量S进行变分处理得到，其中p为广义动量，q为广义坐标.

通过将费马原理与能量守恒时的莫培督定理进行类比定义了等效实物粒子的动量p=n(r)，当我们将实物粒子的质量定为1,可以得到该粒子的速度为v=n(r)，该粒子的动能为

由能量守恒定律，我们定义总能量为零，则等效势能场

该粒子在势场中的受到的保守力

这里构建类比虽然缺少严谨的科学性分析，但是与由程函方程出发推导出来的光线方程具有一致性，由此，可以作为变折射率光学问题的一种解题手段.本文将光在介质中的传输问题转化为研究该粒子在该势场中的运动问题.

1.1 折射率在直角坐标系中沿y轴变化

光的折射定律可以看作粒子在通过两个法向方向分布的势场时粒子在经过折射面时的切向速度vτ不变进行推导.本文着重分析变折射率问题.

光线轨迹如图1所示，其中初状态光线和水平方向的夹角记为θ0，所处位置的折射率为n0，则粒子在运动过程中x方向做匀速直线运动

vx=n0cosθ0

在轨迹上任意一点的速度大小由n决定，即

v=n(y)

则在轨迹上任意一点的y方向的速度大小为

光线的轨迹方程可以用x方向的匀速直线运动与y方向的变速运动合成来进行分析，轨迹中任一点的斜率

图1 光在沿y轴变化变折射率介质中传播轨迹示意图

下面我们以第32届中学生物理竞赛决赛第8题的前两问为例进行具体分析.

图2 激光传播路径示意图

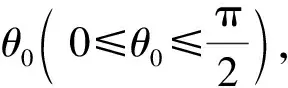
(2)假定目标A位于第一象限.当目标A的高度为ya时,求激光发射器可照射到的目标A的最大x坐标值xa-max.

vx=n0sinθ0

轨迹中高度为y处粒子的y方向的速度为

则在该点的斜率

移项积分处理

即

利用初始条件x=0时，y=0可得

代入化简可得轨迹方程

第(2)问从力学角度思考当粒子沿x轴方向入射时达到ya高度在水平方向运动距离最远.即θ0=90°，代入轨迹方程，由

解得

1.2 当折射率在极坐标系下沿径向r变化

实际生活中，例如地球表面的大气变折射率分布问题，经常会遇到折射率沿径向变化，对于该类问题，从粒子的角度，我们采取如图3所示的极坐标进行分析.

由于其势能场

故其为一个有心势场，可以利用角动量守恒来求解，在运动轨迹上任一点有

rpsinφ=r0p0sinφ0

其中r0,p0,φ0是初状态的动量以及速度与位矢间的夹角，即

rn(r)sinφ=r0n0sinφ0

又

可得极坐标中轨迹的斜率与r的关系

仍然可以利用力学方法处理光线模型，下面我们看一个实际例子作为分析.

【例2】(高中物理奥赛指导P377例4)某行星上大气的折射率随着行星表面的高度h按照n=n0-αh的规律而减小，行星的半径为R，行星表面某一高度h0处有光波道，它始终在恒定高度，光线沿光波道环绕行星传播，试求高度h0.

移项后可解得

2 在变介质光纤传播中的应用

第36和37届复赛的光学题都考到了阶跃型光纤，可见光纤模型的重要性.阶跃型光纤在传输过程中不同入射角进入的光线在均匀介质中传输的路径不同，易得入射角越大，光程越大，因此对于固定周期的脉冲信号，由于入射角的差异使得光纤中的传输时间不同，产生的时间差会导致光脉冲信号出现展宽.所以该类光纤会导致高色散，传输频带宽度受限，在长距离信号传输中已经被淘汰，取而代之的是渐变型的光纤[5].

因此，对渐变型光纤的光路进行定量分析是必要的.相较于阶跃型的光纤，特殊的径向折射率分布使其具有自聚焦特性，具体可分为抛物线型和双曲割线两种类型的折射率分布[6].其中抛物线型的折射率介质问题在高中竞赛中也有出现.本文用哈密顿光学模型从力学角度分析抛物线型折射率光纤的轨迹，从而说明其自聚焦性.

图4 圆柱形光纤传输示意图

vx=n0cosφ0

轨迹上某点r方向的速度为

在r方向运动的能量关系式满足

即

则粒子在r方向做简谐振动，振动的角频率ω为

当vr=0时

则振幅A为

则r方向的运动学方程为

光线方程为

表明光线是正弦曲线，O点出射后，光线与x轴的第k个交点的坐标为

式中φ0为小角度时，cosφ0=1，则

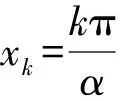
图5 抛物线型折射率光纤自聚焦光线图像

通过该例我们也可以发现对于自聚焦性的光纤，入射角不仅要满足内外纤层的全反射条件，还需要满足小角度以实现在不同角度入射的光线与x轴的交点近似一致，最终获得良好的聚焦特性，减小由于传输时间不同导致的色散，避免了光信号的畸变，其光线图像如图5所示.

3 光纤传输过程中的扩展分析

上例我们通过力学方法分析了抛物线型折射率分布的光纤模型，其折射率分布函数满足

通过分析发现其需要满足小角度入射才能保证所有的子午射线都具有相同的周期.其小角度的限制条件仍然是一个缺点.由此，引入双曲正割型折射率分布的介质，其折射率分布函数满足

通过级数展开可以得到

式中En为n级欧拉数，当小角度入射时r为小量，双曲正割型与抛物线型相同.

通过严格的数学运算，在双曲正割媒质中，从一点发出的子午光线无论其孔径角的大小，其在一个周期中走过的光程是严格相等的[6]，所以在这种媒质中，一轴外点发出的子午光线又可以聚焦于一点.

4 总结

本文用哈密顿光学的方法通过将光线的传播类比于粒子在特殊势场中的运动来解决渐变型折射率中光线传输的问题，对最为典型的折射率沿直角坐标系y轴变化以及极坐标系极轴r轴结合实际例题进行了分析.在此基础上，对于最重要的光纤传输模型进行了深入分析，用该思路分析了折射率呈现抛物线型的自聚焦模型.在此基础上，笔者为了让学生更好地理解光纤传输的研究思路，深入介绍了在不满足小入射角时引起的时间延迟效应从而导致的信号的畸变，并且通过双曲割线型折射率分布来得以解决.哈密顿光学法在解决变折射率光的传播路径等问题中拥有简单快速的优点，且对于今后学生在从事光纤传输等方向的研究以及对光线光学理论的学习时，具有事半功倍的引导作用.