椭圆曲面摆参数振动的数值计算及仿真*
2022-05-19何烈云浙江警察学院交通管理工程系浙江杭州310053李国军浙江警察学院公共基础部浙江杭州310053
何烈云(浙江警察学院交通管理工程系 浙江 杭州 310053)李国军(浙江警察学院公共基础部 浙江 杭州 310053)
根据傅利叶变换所有周期振动均可分解成几个(甚至无穷多个)简谐振动,因此简谐振动是一种简单的机械振动形式,任何一本大学物理教材力学部分都将简谐振动作为机械振动基础内容介绍.典型的简谐振动模型装置有弹簧振子和单摆,除此之外,在习题中还会遇到球面摆问题,小球在一个半径很大的光滑凹球面上做较小幅度摆动,讨论小球摆动规律.教师在球面摆拓展教学中,往往从增大摆角或增加小球摆动的阻尼作用两个方面增加问题的复杂程度.在一次讲授球面摆习题时,有学生问及若将球面换成椭圆曲面,小球振动规律又会如何变化?小球在两种不同曲面上摆动时最大区别在于“摆长”是否恒定,摆长指的是球心距离椭圆中心距离.在椭圆曲面上摆动时摆长符合一定规律变化,因此小球摆动属于一种参数振动,不满足简谐振动的条件.
参数振动求解较为复杂,一般的力学教材没有作深入介绍,但国内外许多学者们对不同类型的参数振动研究比较感兴趣.文献[1]将量子高级绝热近似方法用来求解变摆长单摆的振动,研究表明,当摆长缓慢变化时,其振动形式近似为简谐振动.文献[2]研究表明,从能量转换角度,任意振幅的单摆均做周期运动,其振动周期可采用椭圆积分形式表示.由于椭圆积分形式运用起来不够方便,许多学者在此基础上构造了不同的近似函数描述单摆在任意角度下的振动周期.文献[3]构造的近似函数最为简单,该函数只要摆幅控制在90°以内,单摆周期数值计算结果误差不到1‰.文献[4]将椭圆积分形式作泰勒展开,构造了新的单摆周期近似公式,采用该公式计算单摆周期时,只要振幅在114°的范围内,单摆周期数值计算结果相对误差小于 1‰.文献[5]重点研究了阻尼及外界驱动力对单摆周期的影响,并分析了具体的运动形式.文献[6]通过单摆运动与铅直运动耦合机械模型,研究了变摆长单摆运动特性,通过高精度数值解法得到了变摆长单摆的近似解.文献[7]利用龙格-库达法,结合MATLAB软件得到了非线性单摆振动的多种图像.
上述研究文献内容都属于参数振动,且都是针对单摆从不同方面作了拓展.参数振动形式是多种多样的,本文以椭圆曲面摆为研究对象,构建小球摆动的动力学方程,运用数值分析和计算机数值仿真的方法,讨论小球在椭圆曲面摆动的运动规律,分析影响小球摆动周期的因素.
1 椭圆曲面摆动力学方程及求解
椭圆曲面摆装置是将球面摆装置中的球面改成了椭圆曲面,该模型装置剖面图如图1所示.图中O为平衡位置,O′为椭圆的几何中心点,θ为小球摆角;d0为平衡位置到椭圆几何中心的距离,即椭圆竖直方向半轴长度,d是小球球心与椭圆中心的距离(下称摆长);G为小球重量,Fn为小球受到曲面的作用力,f为小球摆动时受到的阻力,在速度不快时,可认为阻力与速度大小成正比且方向相反[8],比例系数记为γ.

图1 椭圆曲面摆装置示意图
1.1 椭圆曲面摆动力学方程
设小球质量为m,根据小球的受力特点,运用定轴转动定律,摆动过程中的动力学微分方程满足
(1)
由椭圆方程可知,摆长d满足
(2)
式(2)中a为椭圆长半轴长度,b为短半轴长度.
令阻尼系数
联立式(1)和式(2),可得到小球摆动的动力学微分方程
(3)
1.2 椭圆曲面摆动力学方程数值计算
根据二阶微分方程知识,式(3)属于二阶变系数非齐次微分方程,无法给出确切的解析解.若给定初始条件,式(3)可以采用龙格-库达法给出方程的计算值,并利用计算机进行数值仿真,省去求解微分方程的复杂过程.该方法基本思想是在已知方程导数和初值初始条件,用区间上的若干点进行加权平均得到平均斜率,并经过多次迭代,获得方程的数值解[9],其中四阶龙格-库塔法最为经典,具有精度高、误差小的优点[10].式(3)四阶龙格-库塔法计算基本步骤如下.首先将式(3)用角速度参数表示降为一阶微分方程
(4)
此时θ=f(θ,t),ω=g(θ,t),设初始条件θ(t0)=θ0,ω(t0)=ω0,确定时间间隔h=δt,采用迭代法依次求出f(θ,t)和ω=g(θ,t)曲线斜率k.最后采用显式龙格-库达法式(5)和式(6)求得相应位置角位移和角速度数值
(5)
(6)
式中k1j和k2j分别代表f(θ,t)和ω=g(θ,t)曲线斜率.为了提高计算精度,可以缩短时间间隔h值.四阶龙格-库达法数值计算量大,在实践中一般是采用计算机程序语言实现,并绘制f(θ,t) 和ω=g(θ,t)曲线图像.
2 椭圆曲面摆基本振动规律
设椭圆水平方向长半轴a=2 m,竖直方向短半轴b=1 m,设初始条件ω0=0,θ0=arctan(0.2),阻尼系数β=0.运用MATLAB绘制液体晃动角速度和角加速度图像,得到如图2所示的θ-t图像、ω-t图像和θ-ω图像.

(a) θ-t图像

(b) ω-t图像

(c) θ-ω图像
图2(a)、(b)、(c)图像可知,在不考虑阻尼作用时,椭圆曲面摆小球摆动类似简谐振动,小球运动规律可以用正弦或余弦函数表示,图像振幅和相位取决于初始条件值.因此无阻尼椭圆曲面摆的解形式可以写成

(7)
式(7)中,φ为摆幅,T为小球摆动周期,由图像可知T≈1.91 s.
3 椭圆曲面摆周期影响因素
接下来分别通过改变阻尼系数、椭圆曲面几何尺寸及振幅大小,讨论椭圆曲面摆周期特性.
3.1 阻尼系数对周期的影响
设椭圆长半轴a=2 m,短半轴b=1 m,初始条件ω0=0和θ0=arctan(0.2),阻尼系数β大小分别为0,2,5.27,10,绘制图3(a)、(b)椭圆曲面摆的θ-t图像和θ-ω图像.

(a) θ-t图像
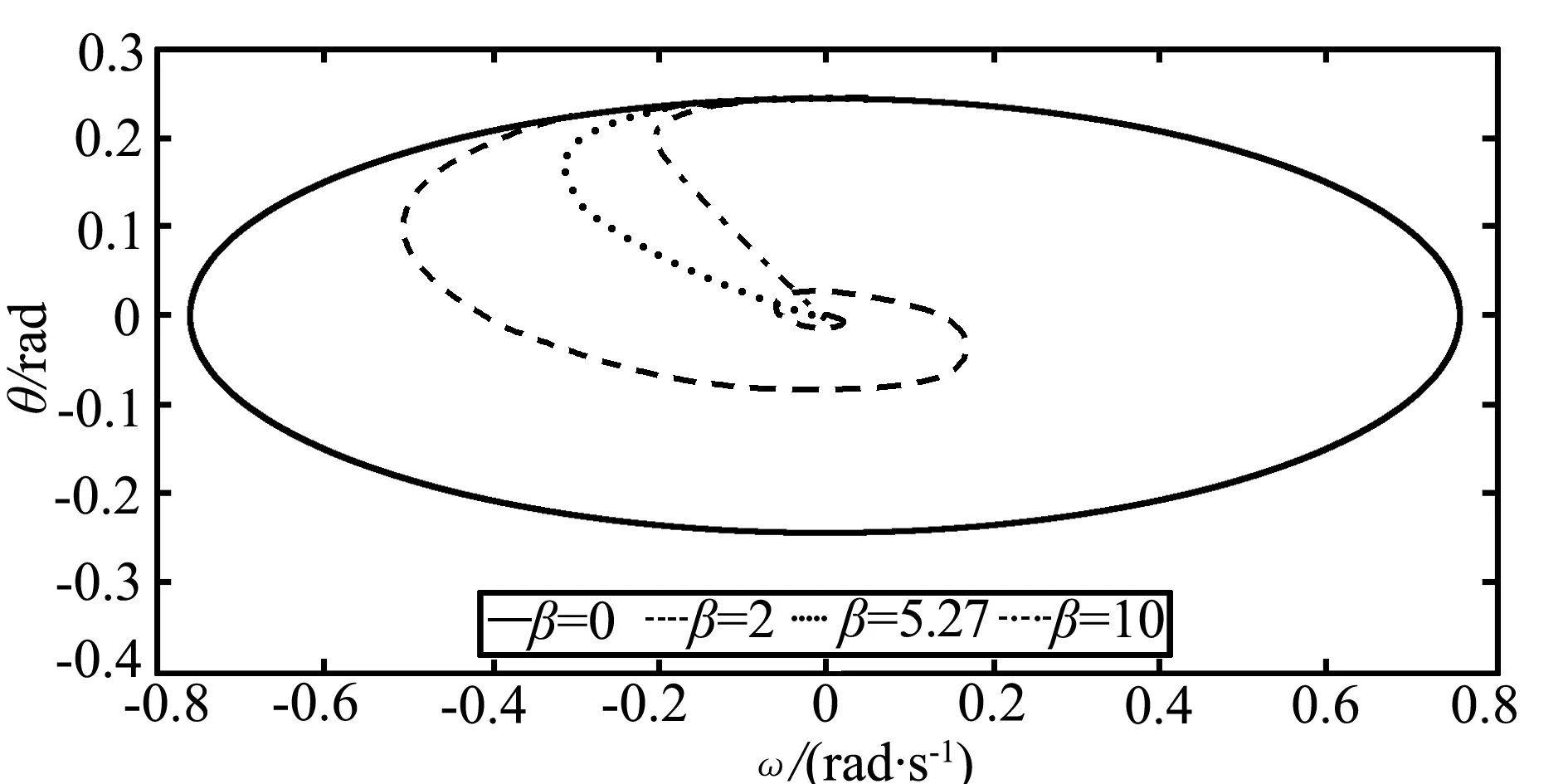
(b) θ-ω图像
图3表明:
(1)当β=2处于欠阻尼状态,小球的摆幅随着时间推移逐渐减小,直到最终停留在平衡位置处,而且振动周期大于同一椭圆曲面摆装置无阻尼振动周期T;

(3)当β=10时处于过阻尼状态,小球从开始摆动后慢慢回到平衡位置并停下来.
3.2 椭圆曲面几何尺寸对周期的影响
讨论椭圆曲面几何尺寸对周期的影响时设β=0,初始条件ω0=0,θ0=arctan(0.2),分两种情况:
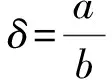
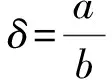
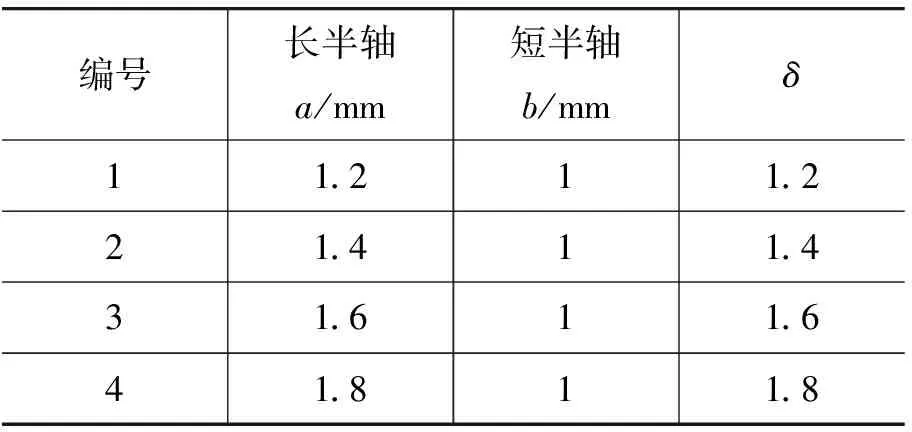
表1 短半轴固定,长半轴增大

表2 长半轴固定,短半轴增大
最终得到图4(a)、(b)所示的θ-t图像.

(a) 短半轴固定,长半轴变化

(b) 长半轴固定,短半轴变化
图4表明,椭圆的长半轴和短半轴长度增大,小球摆动周期均增长.但短半轴的变化对小球摆动周期影响显著,而长轴的变化对小球摆动周期影响极小.
3.3 振幅对小球摆动周期的影响
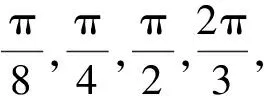

图5 振幅变化的θ-t图像
图5表明,伴随着摆动振幅增大,小球的摆动周期也变长.
4 结束语
(1)在椭圆曲面摆装置中,小球摆动过程中摆长按一定规律变化,属于一种参数振动.
(2)小球摆动的动力学方程为二阶变系数齐次微分动力学方程,运用龙格-库达法可以给出方程进行数值解,结合MATLAB软件绘制角位移和角速度图像.
(3)椭圆曲面摆振动与单摆振动类似,在无阻尼状态时符合正弦变化规律,伴随着阻尼系数、振幅、椭圆曲面长短轴增大,小球摆动周期也相应增大.
