基于 CNN-LSTM 的齿轮箱复合故障状态监测研究
2022-05-19王靖岳王浩天王军年
王靖岳,高 天,王浩天,王军年
1沈阳理工大学汽车与交通学院 辽宁沈阳 110159 2吉林大学汽车仿真与控制国家重点实验室 吉林长春 130025 3沈阳航空航天大学自动化学院 辽宁沈阳 110136
齿 轮箱作为核心传动装置,广泛应用在汽车、轨道车辆、风电机组等各大领域。随着大量齿轮箱被投入使用,其在工作中发生故障的情况也越来越多,齿轮箱的状态监测技术也因此发展起来。由于监测仪器逐渐趋向于智能化,因此振动信号分析监测方法成为当前研究的重点。目前机械设备的监测是通过对设备运行状态进行数据采集,经人工或智能对比相关运行参数的阈值指标,来判断设备的运行情况。
目前国内在这方面的应用技术已相对成熟,深度学习等智能算法在此领域得到了广泛的应用[1-7]。马芸婷等人提出主成分分析结合 SAE 深度学习方法的齿轮故障诊断,准确率达到 96% 以上[8];李亚鑫采用深度对抗卷积神经网络构建了迁移学习故障诊断方法[9];许超设计了齿轮箱的状态监测软件,能通过监测齿轮箱的温度、主轴转速等物理参数和振动参数来实现齿轮箱的状态监测,并配备有振动信号分析的离线分析系统[10];窦春红采用奇异谱增强故障特征,并将多尺度符号动力学熵引入状态监测中,量化地揭示了数据的时空间状态[11];鲁统超等人将 CNN-LSTM 组合网络结合高斯混合模型构建了一个航空发动机故障识别网络[12],识别准确率较高。
齿轮传动系统出现复合故障时,传感器采集到的复合故障信号,是各单一故障信号从各自的故障部位经过复杂的传递路径耦合在一起的混合信号,其中较弱的周期性特征会被其他成分淹没。混合模型识别网络能改进单一模型的缺点,样本输入 CNN 网络,通过卷积池化等操作提取数据之间的高级特征,并将特征输送到 LSTM 网络中。
1 神经网络
1.1 卷积神经网络
卷积神经网络 (Convolutional Neural Network,CNN) 这一概念最早由 Yann Lecun 于 20 世纪 80 年代提出,是受到生物神经学中感受野的启发而发展起来的一种前馈神经网络结构模型。其作为一种有监督深度学习算法,端到端的数据处理模式,由于特征提取阶段不需要人工选择,而被广泛应用在各个领域的设备状态监测中[13-14]。
1.2 长短期记忆神经网络
长短期记忆神经网络 (Long Short Term Memory Network,LSTM) 是一种变型式的循环神经网络[13]。其特点是增加了遗忘门、输入门和输出门结构,从而决定记忆权值,选择控制单元的状态,因此不会发生普通循环网络可能出现的梯度消失现象。LSTM 是当前发展较为稳定有效的循环神经网络架构,在处理时间序列上拥有更高的精度。其网络基本单元如图 1 所示。
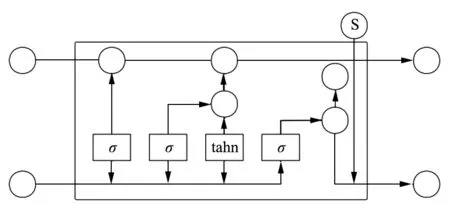
图1 LSTM 结构示意Fig.1 Structural sketch of LSTM
2 基于 CNN 和 LSTM 的齿轮箱复合故障状态监测研究
单独神经网络在机械设备故障诊断中的应用局限在于处理复杂问题时的运算速度普遍较慢,难以适应工业需求,准确率未能达到预期,网络的稳定性较差。针对上述问题,学者们开始研究将多种神经网络组合成为新的深度学习算法,将 CNN 结合 LSTM 的网络结构提出来,并广泛应用于工业设备故障特征的研究。
笔者构建了一个 12 层神经网络,其网络体系结构组成如图 2 所示,将折叠层和卷积核合并为卷积层。其工作原理如下:一维时间序列经第 1 层输入层输入后到达第 1 个卷积层,卷积核为 2×1;然后连接 ReLU 激活层,再经过第 2 个卷积层,卷积核为 2×1;再经过第 2 个 ReLU 激活层,此时数据为 32 个特征图;随后接序列反折叠层,其作用是将目前多维的数据一维化,即将特征图转换为一维序列,以便输入 LSTM 网络层;经过 LSTM 后连接全连接层,然后连接 Softmax 激活层;最后输出网络对测试集状态监测的准确率。

图2 网络的层数及结构图Fig.2 Number of layers and structure of network
3 试验验证
笔者的研究数据来自于 HFXZ-I 型齿轮箱复合故障试验台,如图 3 所示,该试验台主要由驱动电动机、平行齿轮箱、磁粉制动器等组成。

图3 齿轮箱试验台Fig.3 Gearbox test bench
选择齿轮箱试验台正常状态和 3 种故障状态的振动信号作为分析对象。3 种故障状态分别是齿轮轮齿磨损故障、轴承外圈故障以及 2 个故障同时存在的复合故障。因此共可以分为 4 种工作状态:即正常工作状态、齿轮故障状态,轴承故障状态以及复合故障状态,状态代码分别设为 1、2、3、4。齿轮箱振动信号的时域波形如图 4 所示。

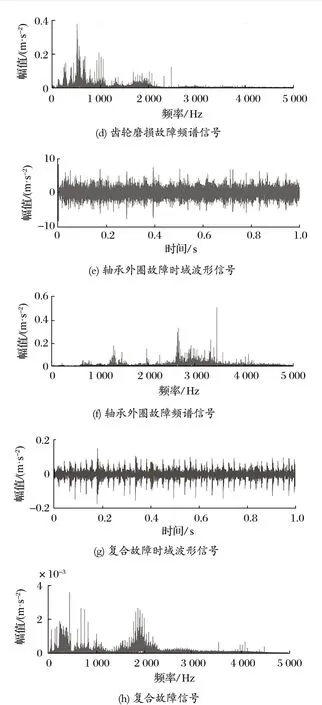
图4 齿轮箱振动信号时域波形图Fig.4 Time domain waveform of vibration signal of gearbox
首先对数据进行预处理。一维振动信号经过预处理后的 4 种工作状态共划分成 3 960 个样本,并随机打乱。每个样本的形式为 [10,1,1],按 7∶3 的比例分成训练集和测试集。设置最大训练次数为 100,初始学习率为 0.01,正则化参数为 0.000 1,学习下降因子为 0.1,并设置为每经过 60 次训练进行一次迭代,学习率变为 0.1 倍。最后,输出 CNN-LSTM 网络对齿轮箱 4 种工作状态的状态识别准确度,将测试集中正常工况设为 1,单故障分别设为 2 和 3,复合故障状态设为 4,测试网络的检测准确率。为确保减少偶然性,将同样数据状态检测流程进行 3 次,取其平均值。
其中任意一次的 CNN-LSTM 网络运行的监测准确率变化图、损失函数变化图和测试集的监测准确率如图 5 所示。

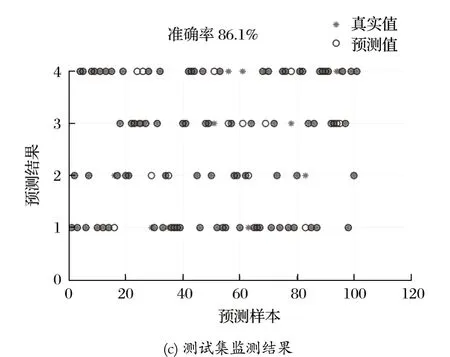
图5 CNN-LSTM 网络运行结果Fig.5 Operation results of CNN-LSTM
由图 5 可以看出,运行的工作状态监测准确率达到 86.1%。分析测试集的监测结果发现,只有监测系统对于正常工作状态的判别非常精确,复合故障状态的判别结果较为精准,只有少许误差,而另外 2 次的运行准确率分别为 87.1% 和 86.3%。3 次运行的平均准确率为 86.4%。一般来说,对于不同类别复合故障工作状态的识别正确率达到 85.0% 以上就足以证明该模型的实用性和稳定性。
为证明 CNN-LSTM 方法的有效性,分别用同样的数据进行 CNN 模型分析和 LSTM 模型分析。同样的数据进行 3 次测试,取准确率的平均值,其中 1 次训练过程如图 6 所示。分析测试集的检测结果发现,LSTM 网络对于轴承单故障形式的判别误差较大,对于复杂调制信号的特征不能有效学习,其他状态的监测则相对精确。其余 2 次的 LSTM 网络监测准确率分别为 81.0% 和 78.0%,可以看出仅靠 LSTM 网络达成监测功能稳定性较差,平均准确率为 80.3%。

图6 LSTM 网络监测结果Fig.6 Monitoring results of LSTM
仅使用 CNN 网络同样运行 3 次,其中 1 组训练过程和结果如图 7 所示。其余 2 次的 CNN 网络监测准确率分别为 0.78% 和 0.83%,平均准确率只有 0.76%,学习率曲线与损失率曲线都不理想,训练成果较差,可能由于输入的数据导致梯度问题,稳定性远低于组合网络。


图7 CNN 构建的网络监测结果Fig.7 Monitoring results of network built by CNN
4 结语
通过在 CNN 和 LSTM 两种网络模型理论基础上建立 CNN-LSTM 齿轮箱状态监测模型,对齿轮箱试验台采集的复合故障数据进行训练与测试,平均准确率达到 86.4%,证明了该模型的有效性与稳定性。而仅用 LSTM 构建的检测模型和仅用 CNN 构建的监测模型准确率均低于组合网络。
