配合间隙对液压重载机械臂定位精度的影响

2022-05-19申浩翰王富勇胡同海杨柳松夏红峰

矿山机械 2022年5期

郝兵，申浩翰，王富勇，胡同海，杨柳松，夏红峰，李杨

1中信重工机械股份有限公司河南洛阳 471039 2矿山重型装备国家重点实验室河南洛阳 471039 3洛阳矿山机械工程设计研究院有限责任公司河南洛阳 471039 4金堆城钼业汝阳有限责任公司河南汝阳 471200

随着现代工业的快速发展，矿山设备逐渐趋于大型化，大型设备的维护保养及辅助生产对工作环境、安全及效率提出了更高的要求[1-2]。重载机械臂有助于提高大负载作业的工作效率，降低作业难度和人工成本[3]，在矿山领域得到了广泛的应用。

国内外学者对重载机械臂进行了大量的研究工作，取得了较大的进展。熊小辉[4]对重载机械臂模型进行了运动分析和控制系统仿真，研究了机械臂设计参数对性能、功能指标的影响规律；郝兵等人[5]对重载机械手的多体动力学刚-柔耦合模型进行仿真研究，结合有限元分析，为机械臂的液压缸、电动机和结构设计提供了参考；赵天闻等人[6]利用 ADAMS 软件对重载机械臂末端的运动轨迹进行多体动力学分析，给出了一种机械臂平稳运动的方法；楚旭等人[7]为提高磨机换衬板机械臂的定位精度和运行平稳性，通过仿真研究，设计了一种电液控制策略；毛龙锐等人[8]通过对重载机械臂进行多体动力学仿真研究，优化了末端输出功率；徐赛华[9]对液压重载机械臂进行了有限元和多体动力学分析，提出了一种最优截面参数的轻量化设计方法，提高了定位精度；S.C.Liu 等人[10]提出了一种无需外部传感器的工业机器人触觉控制方法，提高了机械臂与操作工人的协同装配效率；W.Q.Lu 等人[11]确定了柔顺装配机械手驱动电动机的初始位置，从而实现了装配机械手的高转矩快速启动。

以上研究为重载机械臂的设计、控制和定位精度等方面提供了大量参考，但是对重载机械臂定位精度影响因素的研究仍存在空缺。为此，笔者以配合间隙对重载机械臂定位精度的影响为目标，进行间隙配合函数构建方法的研究。

1 配合间隙的确定

为了实现对多段伸缩式重载机械臂各臂节间配合间隙的模拟，首先要对机械臂伸缩特性进行分析，针对单段伸缩机械臂建立简化模型，找到机械臂在伸缩过程中的关键点，并对关键点的运动状态进行研究。

1.1 伸缩式机械臂简化模型

伸缩式机械臂简化模型如图 1 所示，主要分为内筒体和外筒体，筒体内部与液压缸相连。两筒体形状相似，内筒体较外筒体尺寸更小，使得内筒体能够将其大部分结构置于外筒体中。在机械臂进行伸缩运动时，连接在内外筒体上的液压缸对筒体提供推力，使得内外筒体产生相对轴向运动。

图1 伸缩式机械臂简化模型Fig.1 Simplified model of telescopic robotic arm

由图 1 可以看出，机械臂的内外筒体也可以看作是机械臂的内外臂，内外臂间存在一定的间隙。虽然实际结构中使用了如橡胶之类的弹性体在间隙的合适位置进行填充，但是考虑到装配需要和填充物的弹性变形，间隙的存在不可避免。通常情况下间隙尺寸较机械臂而言非常小，为便于分析，绘制了机械臂收缩状态示意图，如图 2 所示。图 2 中，黑色实线代表外臂且互相平行，两线段间的距离即为配合间隙d，黑色虚线代表内臂。根据左侧坐标系定义水平方向为x向，竖直方向为y向。两臂节的关键点已标出，其中关键点A、B、C位于内臂，A′、B′位于外臂。各关键点的x、y轴坐标由关键点代号加x、y下角标表示。

图2 配合间隙示意Fig.2 Sketch of fit clearance

1.2 臂节关键点的运动方程

由于图 2 中机械臂所处的状态为收缩状态，所以Ax′=Cx，且d＝。内臂水平方向的倾角α也可求出。

式中：LBC为线段BC的长度。

此时内臂的关键点C相较于不考虑配合间隙时的理论位置，向y轴负方向偏移了 0.5d；关键点B向y轴正方向偏移了 0.5d；关键点A向y轴负方向偏移了 0.5d+LACsinα。

当机械臂进行伸缩运动将内臂伸出时，图 2 中各关键点的相对位置变化情况如图 3 所示。内臂的伸出长度可表示为LCC′，内臂倾角由α变化为α′，且可表示为

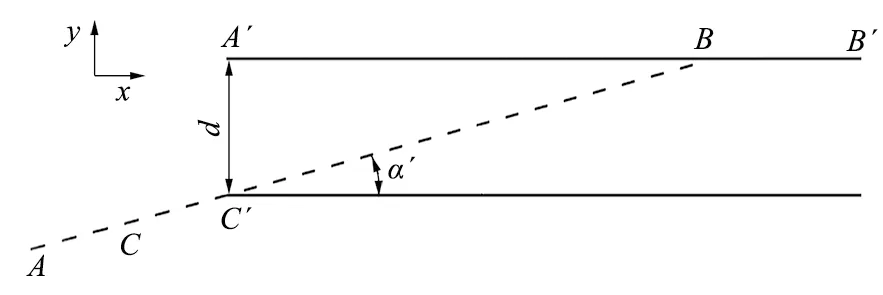
图3 内臂伸出示意Fig.3 Sketch of inner-arm extension

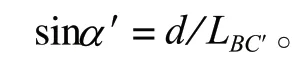
此时内臂上关键点C向y轴负方向偏移了d/2′；B的偏移量较收缩状态无变化，仍为d/2；A向y轴负方向偏移了

综上所述，关键点A、B、C基于中心轴y轴的偏移量方程为

将式 (1) 中的三角函数转换为线段表示

将式 (2) 中各方程的自变量均由内臂伸出长度LCC′替代，可得

此方程即为关键点A、B、C随内臂伸出长度LCC′变化而变化的y轴运动方程。

1.3 限位方程和接触函数的确定

在确定了内臂各关键点的运动方程后，下一步就是将运动方程引入试验。多体动力学软件 ADAMS 中的多种接触函数能够满足不同的使用需求，结合笔者需要解决的工程问题，最终选用双边接触函数 (Twosided Impact in Contact Function) 作为试验中内外臂节间的接触函数。

双边接触函数的工作原理是将不同零件上两个关键点的相对位置关系和相对速度关系，代入设定好的限位方程和接触力方程，来判断零件之间是否接触，并在两个关键点上施加相互作用力。由于试验中仅考虑配合间隙对机械臂定位精度的影响，因此只需通过限位方程来约束关键点的相对位置即可。接触力需要在不减缓求解速度的前提下设定为一个较大的数值，于是通过大量的试验，最终寻找到一组合适的接触力方程，设定参数能够满足上述需求。

函数中各参数的设置如图 4 所示，各设定参数按照不同功能可分为三类。

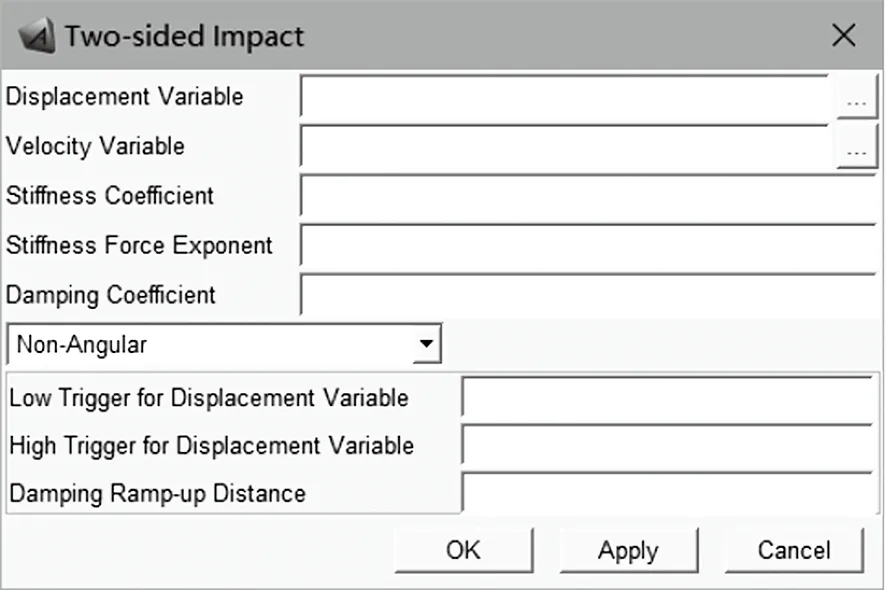
图4 双边接触函数设定Fig.4 Settings of two-sided impact contact function

(1) 第一类为输入参数，即需要从模型中引入的参数，Displacement Variable 代表两关键点间的相对位置，Velocity Variable 代表两关键点间的相对速度；

(2) 第二类为作用力参数，即决定两关键点间相互作用力大小的参数，Stiffness Coefficient 代表刚度系数 (设定为 1×108)，Stiffness Force Exponent 代表刚度力指数 (设定为 1.5)，Damping Coefficient 代表阻尼系数 (设定为 1×103)，Damping Ramp-up Distance 代表阻尼斜坡距离 (设定为 1×10-10)；

(3) 第三类为限位参数，即用于约束关键点间相对运动范围的参数，High Trigger for Displacement Variable 代表高限位，Low Trigger for Displacement Variable 代表低限位。

通过上述分析，结合式 (3) 中给出的关键点限位方程，可得出关键点C在x轴方向上的双边接触函数，转化成 ADAMS 为：

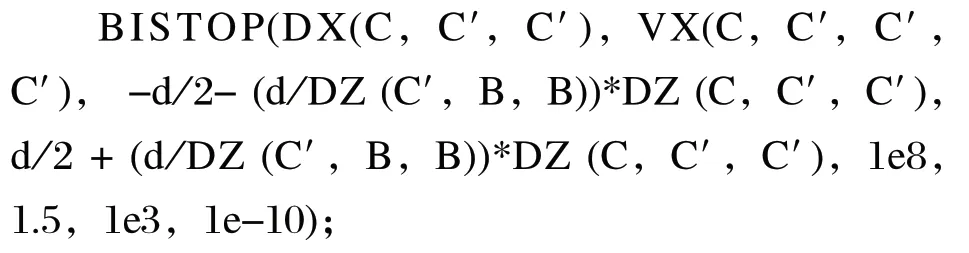
关键点B的x轴双边接触函数为：

同理，关键点C的y轴双边接触函数为：

关键点B的y轴双边接触函数为：

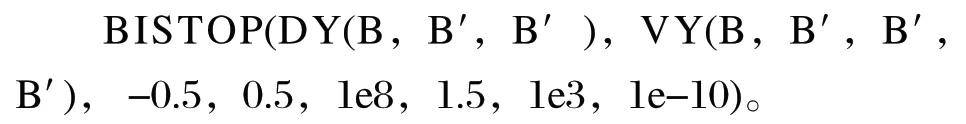
2 双边接触函数的验证及其在重载机械臂上的应用

在建立了用于模拟配合间隙的双边接触函数后，需要对其可靠性进行验证，然后即可将其应用于伸缩式液压重载机械臂，研究配合间隙对机械臂定位精度的影响。

2.1 双边接触函数的验证

为了验证双边接触函数的可靠性，建立了简化后的机械臂 ADAMS 模型，并引入双边接触函数来对关键点的运动轨迹进行跟踪。

简化后的机械臂 ADAMS 模型仅保留了内外臂，如图 5 所示。内臂和外臂臂右端对齐，内臂长度为 500 mm，外臂长度为 400 mm，径向间隙d拟定为 1 mm。模型轴向方向向左为z轴正方向，在内臂左端沿y轴负方向施加 30 kN 的力，如图 5 中空心箭头所示。

图5 简化后的机械臂 ADAMS 模型Fig.5 Simplified ADAMS model of robotic arm

首先将图 2 中各关键点的理论位置映射于图 5 中的 ADAMS 模型，即可确定各关键点在模型中的位置和编号。图 5 中各向上箭头的位置即为关键点的坐标，关键点的位置和编号如表 1 所列。把双边接触函数中的各关键点名称替换为此仿真试验中的关键点编号，即可确定此仿真试验中关键点C、B在x、y轴方向上的双边接触函数。

表1 关键点编号和位置Tab.1 ID and location of key points

确定了 ADAMS 模型并建立双边接触函数后，就可以对双边接触函数进行验证。首先是将图 5 中的模型参数代入式 (3)，对各关键点的运动轨迹进行计算。根据模型可知d＝1 mm，LAC＝100 mm，LAB＝500 mm。现假定内臂以 10 mm/s 的速度抽出，即可得到LCC′相对于时间t的变化方程

将上述参数代入式 (3) 可得关键点A、B、C在y轴方向上的理论运动轨迹

然后在 ADAMS 中对内臂上的关键点C、B利用双边接触函数进行约束，并对内臂施加z轴正方向 10 mm/s 的驱动，得到关键点A、B、C在y轴方向上的运动轨迹。

最后将 ADAMS 中关键点A、B、C的运动轨迹导出并与计算值进行对比，如图 6 所示。

图6 内臂关键点的运动轨迹Fig.6 Motion trajectory of key points on inner-arm

由图 6 可以看出，各关键点运动轨迹的仿真值和理论值基本相同，其相对误差如图 7 所示。相对误差的最大值出现在关键点C的初始阶段，为 0.054%，由于双边接触函数对关键点的约束并非刚性约束，在仿真初期内臂上关键点冲击约束边界而引起的轻微震动，整体误差很小，可以认为双边接触函数能够很好地模拟机械臂各臂节间的配合间隙。

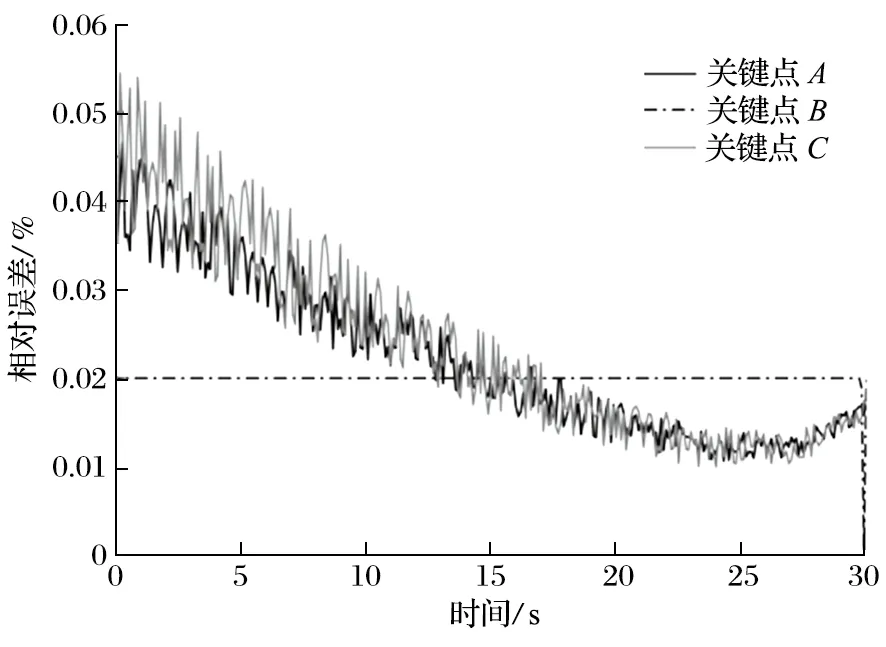
图7 仿真值与理论值的相对误差Fig.7 Relative error between simulated values and theoretical ones

2.2 液压重载机械臂的 ADAMS 模型

在验证了利用双边接触函数模拟配合间隙的可靠性后，便可将其应用于伸缩式液压重载机械臂上，研究配合间隙对机械臂定位精度的影响。

伸缩式液压重载机械臂的 ADAMS 模型如图 8 所示。其中一、二、三段机械臂分别称为内臂、中臂和外臂。各臂节间有液压缸相互连接提供驱动力，外臂右端连接底座，用于支持机械臂的抬起和旋转。

图8 液压重载机械臂 ADAMS 模型Fig.8 ADAMS model of hydraulic heavy-load robotic arm

2.3 机械臂上关键点和接触函数的建立

依照液压重载机械臂的基本结构，对各臂节上的关键点进行定位。定义内臂的 3 个关键点为A1、B1、C1，中臂的 3 个关键点为A2、B2、C2，外臂的 2 个关键点为A3、B3。各关键点的位置和编号如表 2 所列。

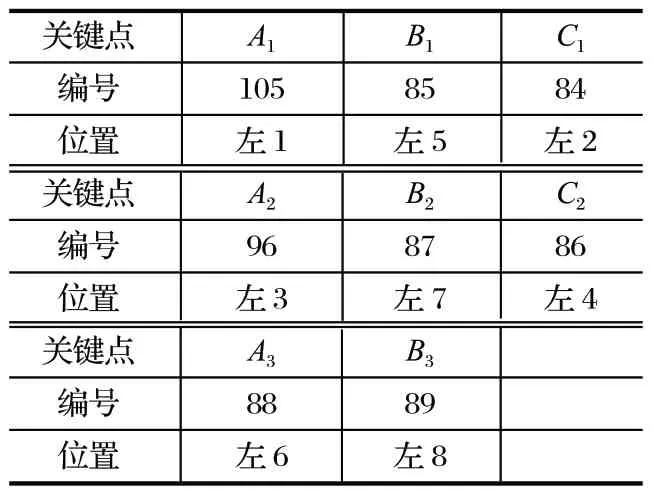
表2 机械臂上关键点的编号和位置Tab.2 ID and location of key points on robotic arm

确定了各关键点的编号信息，就可以确定各关键点的双边接触函数。将关键点的编号代入双边接触函数待定式中即可得到各点的接触函数，其中机械臂的轴向方向为x轴。

内臂上关键点B1在y、z方向的双边接触函数分别为：

BISTOP(DY(85，87，87)，VY(85，87，87，87)，-d/2，d/2，1e8，1.5，1e3，1e-10)；

BISTOP(DZ(85，87，87)，VZ(85，87，87，87)，-d/2，d/2，1e8，1.5，1e3，1e-10)；

内臂上关键点C1在y、z方向的双边接触函数分别为：

BISTOP(DY(84，96，96)，VY(84，96，96，96)，-d/2-(d/DX(96，85，85))*DX(84，96，96)，d/2+(d/DX(96，85，85))*DX(84，96，96)，1e8，1.5，1e3，1e-10)；

BISTOP(DZ(84，96，96)，VZ(84，96，96，96)，-d/2-(d/DX(96，85，85))*DX(84，96，96)，d/2+(d/DX(96，85，85))*DX(84，96，96)，1e8，1.5，1e3，1e-10)；

中臂上关键点B2在y、z方向的双边接触函数分别为：

BISTOP(DY(87，89，89)，VY(87，89，89，89)，-d/2，d/2，1e8，1.5，1e3，1e-10)；

BISTOP(DZ(87，89，89)，VZ(87，89，89，89)，-d/2，d/2，1e8，1.5，1e3，1e-10)；

中臂上关键点C2在y、z方向的双边接触函数分别为：

BISTOP(DY(86，88，88)，VY(86，88，88，88)，-d/2-(d/DX(88，87，87))*DX(86，88，88)，d/2+(d/DX(88，87，87))*DX(86，88，88)，1e8，1.5，1e3，1e-10)；

BISTOP(DZ(86，88，88)，VZ(86，88，88，88)，-d/2-(d/DX(88，87，87))*DX(86，88，88)，d/2+(d/DX(88，87，87))*DX(86，88，88)，1e8，1.5，1e3，1e-10)。

各接触函数中的d为机械臂间的配合间隙，此处待定。

2.4 不同配合间隙对定位精度的影响

在得到了各关键点的双边接触函数后，即可将其代入 ADAMS 模型中，对各关键点进行约束。为研究不同配合间隙对液压重载机械臂定位精度的影响，将配合间隙d分别取 0.5、1.0、1.5、2.0、2.5 mm，并在内臂左端即关键点A1的位置施加一个y轴负方向 30 kN 的载荷。

对机械臂的运动过程进行设定：首先将内臂和中臂各向外伸出 900 mm，并整体向下转动 7°来模拟抓取的过程；然后将机械臂整体向上转动 37°，沿y轴顺时针转动 30°，再向下转动 37°来模拟放置物体的过程；最后内臂和外臂收缩，机械臂整体转动，恢复至初始状态。各运动过程所对应的时间如表 3 所列。

表3 机械臂运动时间设定Tab.3 Motion time settings of robotic arm

配合间隙d分别取 0.5、1.0、1.5、2.0、2.5 mm 时，将机械臂左端点即关键点A1(编号 105) 的x、y、z轴运动轨迹与不考虑配合间隙时的运动轨迹进行对比，偏差量如图 9 所示。图中，横坐标为时间，纵坐标为定位偏差量。各曲线名称由坐标加配合间隙下角标组成，如x0.5为配合间隙 0.5 mm 时，关键点A1在x轴方向上的偏差量。x、y、z轴的偏差量分别对应直线、划线、点划线。

图9 不同配合间隙的定位偏差Fig.9 Positioning deviation at various fit clearance

由图 9 可以看出，y方向即 30 kN 载荷的方向偏差量最大，其次是x方向即机械臂轴向，而z方向偏差量最小。选取运动过程中机械臂左端点在各坐标方向上的最大偏差量，绘制偏差量β随配合间隙d变化的拟合曲线，如图 10 所示。图 10 中，x、y、z方向和总定位偏差β随配合间隙d变化的拟合函数均为正比例函数，斜率分别为 2.60、5.35、1.29 和 6.09，且拟合曲线的R2均大于 0.999，说明拟合效果很好。