多裂纹对裂纹搭接规律影响数值模拟及机理研究

2022-05-18李万渠冯金钰王奕儒

钻采工艺 2022年2期

赵楠，李万渠，冯金钰，王奕儒, 李丽

1四川水利职业技术学院 2中国石油长庆油田苏里格南作业分公司作业一区 3中国石油青海油田分公司勘探开发研究院

0 引言

裂隙广泛存在于岩体结构中[1-2]，在复杂应力条件下裂缝的扩展贯通是导致工程结构失稳的关键因素[3-4]。裂隙的存在降低了材料的刚度与强度，裂纹尖端的应力集中使得工程结构更加容易失效，因此对含裂隙材料及结构的裂隙扩展规律及机理的研究则显得尤为重要。

对于含裂隙材料的失效过程研究较多，在室内试验研究方面：董振兴[5]对水压及双轴作用下的含穿透型裂隙的裂纹扩展进行了室内试验研究，得到了试样的起裂应力、峰值强度及裂纹的发展过程；梅比[6]基于动态焦散线实验系统，对含缺陷的PMMA板进行了三点弯冲击试验；王蒙[7]采用则分离式霍普金森压杆(SHPB)，对SCSCC试样I—II复合型裂纹进行动态断裂试验。

在理论判据方面：李勇明等[8]建立了综合考虑储层所处地应力、多裂纹相互作用的裂纹扩展模型；刘雨等[9]对储层的水力裂缝与天然裂缝的交汇判别准则进行了推导验证。

在数值模拟方面：王杰[10]基于单元破裂法对岩石的裂纹扩展过程进行了描述；蒋明镜[11]基于离散单元法，对含双裂隙标准立方体模型进行了单轴压缩数值模拟试验；王洪建[12]利用扩展有限元法对岩石的断裂过程进行了分析。但是，以往的研究多针对一条或两条类型进行研究，裂隙往往成阵列形式存在于结构中。将实际问题抽象成单条或两条裂隙很难描述裂隙之间的相互作用规律。

1 数值计算理论

1.1 本构关系

岩石的应力—应变关系主要由平衡方程、应力—应变方程及应力—应变关系三个方程来进行描述。

(1)平衡微分方程：

σij,j+Fi=0(i,j=1,2,3)

(1)

式中：σij—计算过程中的总应力,Pa；

Fi—体积力,m3。

(2)应力—应变方程：

(2)

式中：εij—应变张量；

μi—位移张量；

μi，j—位移梯度张量。

(3)应力—应变关系:

(3)

λ、G—Lame常数；

εv—体积应变；

δij—克罗内克函数。

1.2 损伤过程描述

在数值计算过程中，每一个单元的应力分量满足破坏准则时，单元将发生破坏。因此，根据以往损伤处理经验，其损伤后的弹性模量可表达为：

E=(1-D)E0

(4)

式中：D—损伤程度表征；E和E0—已经损伤以及还没有损伤的单元的弹性模量。

同时，当拉应力分量超过材料抗拉强度时，损伤程度表征可以写成：

(5)

式中：ftr—残余抗拉强度,MPa；εt0和εtu—分别表示弹性极限拉伸应变和单元极限拉伸应变。

根据以往数值处理经验，选取Mohr-Columb作为损伤破坏准则，可以同时表征单元的拉伸破坏与剪切破坏，可以表达成为：

(6)

式中：φ—单元的内摩擦角,(°)；fc—单元的抗压强度,MPa。

因此，单元在压缩条件下的损伤程度表征可以表示为

(7)

2 计算模型和参数

建立二维有限元模型，其模型尺寸为150 mm×200 mm，单条裂隙的长度为20 mm，裂隙宽度为1 mm。

模型分为两组，一组为含不同裂隙条数(编号为A)，裂隙角度确定为45°，裂隙条数分别为A1：15条，A2：20条，A3：25条及A4：30条；另一组为含不同倾角裂隙(编号为B)，裂隙条数为15条，裂隙角度分别为B1：25°，B2：45°，B3：75°及B4：90°。模型受到单轴应力作用，采用位移加载模式，加载速率为0.004 mm/计算步。不同工况的数值计算模型如图1所示，模型参数如表1所示。

图1 不同工况数值计算模型

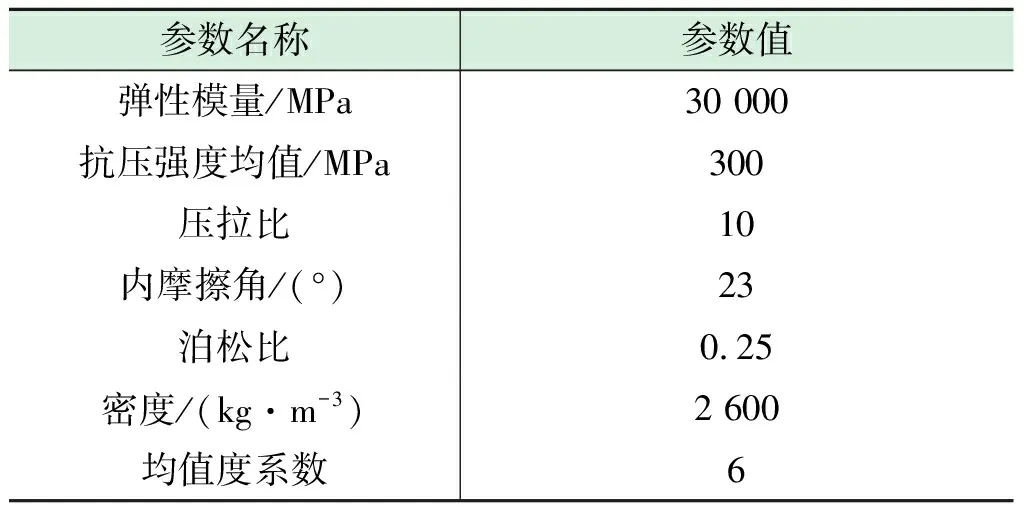
表1 材料基础参数

3 结果分析

3.1 裂纹渐进破坏过程

不同裂隙密度及倾角下的裂纹渐进破坏过程如图2所示。

由图2可见，对于模型A裂隙倾角为45°不同裂隙密度而言，翼型裂纹首先在预制裂纹尖端产生，随后翼型裂纹发展成为拉伸裂纹，逐渐沿着最大主应力方向发展，值得注意的一点是，靠近模型边界的预制裂纹，其翼型裂纹发展程度要大于位于模型内部的预制裂纹，这应是由于边界效应所导致。另外，翼型裂纹扩展后期，反翼型裂纹将从翼型裂纹相反方向产生，翼型裂纹尖端会相互搭接。同时剪切裂纹将从预制裂纹的中部产生，与翼型裂纹、反翼型裂纹相互作用，形成复杂的裂隙网络。预制裂隙的密度越大，模型的边界效应将会减小，同时裂隙网络的发展将会越复杂。

而模型B仅含15条预制裂纹，但就裂隙角度不同的情况而言，模型B预制裂隙的倾角较小时(倾角为25°)，翼型裂纹沿着预制裂纹的内部产生，其扩展方向为最大主应力方向，存在边界效应，与模型A类似。但是对于裂隙倾角较大的情况(倾角为75°)，预制裂隙尖端产生翼型裂纹扩展，但扩展程度较小，随后剪切裂纹主导了模型的破坏，对于裂隙倾角为90°的情况，翼型裂纹同样也并非从裂纹尖端产生，最终模型的破坏模式为以剪切破坏。

3.2 应力—应变曲线

不同裂纹密度及裂纹倾角下的试样应力—应变曲线如图3所示。

由图3可见,单轴压缩下，试样的应力—应变规律主要表现为三个典型特征：①线弹性阶段,此时应力—应变曲线呈现直线规律；②非线性阶段,由于这个阶段裂隙萌生并扩展，其应力—应变曲线偏离直线变形，从而导致模型刚度非线性降低；③残余变形阶段,这个阶段应力跌落，应变增大，模型破坏。

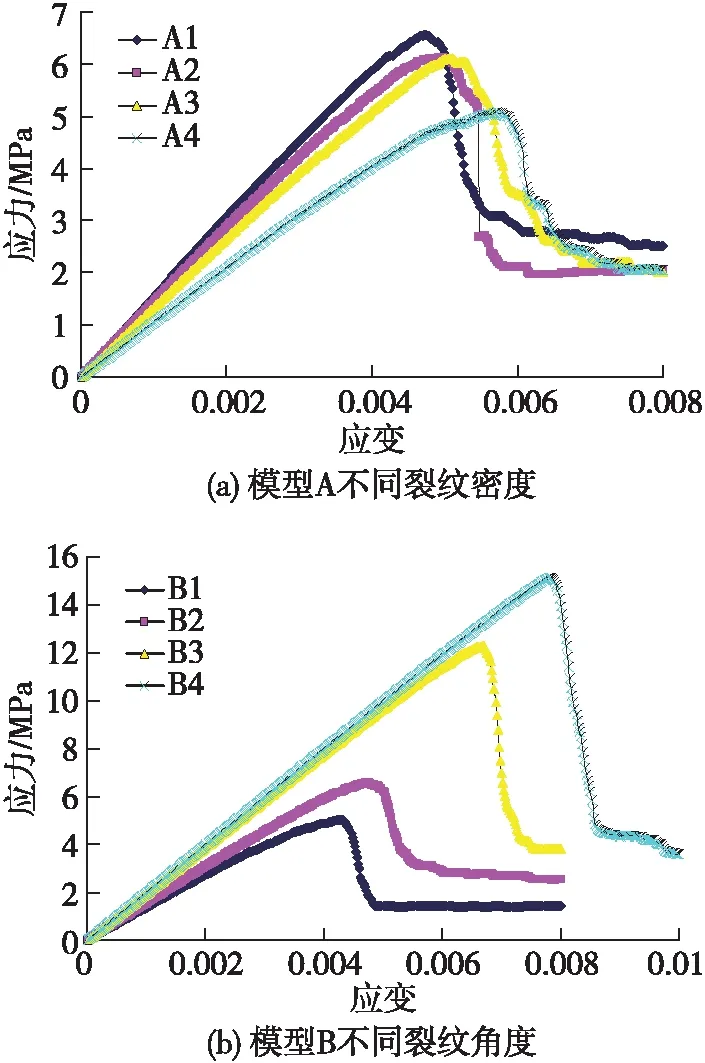
图3 不同裂纹密度及裂纹倾角下的试样应力—应变曲线

对于模型A含不同裂纹密度情况而言，裂纹的密度越大，模型的峰值应力越小。对于模型A1而言，不同裂纹密度模型的峰值强度分别降低百分比为4.3%，4.7%及18.8%，可见裂纹密度对模型峰值强度影响较大，同时当裂纹密度增大到一定程度时模型峰值强度会有一个突然的跌落。对于模型B含不同裂纹角度情况而言，裂隙角度的增大则对模型的峰值强度有一个提高的作用，相对于模型B1而言，不同裂隙角度的增大对模型峰值强度提供的百分比分别为13.2%，45.2%及61.9%，因此就本文

数值模拟结果而言，裂隙角度对模型峰值强度的影响要大于裂纹密度。

4 结果对比

本文的数值模拟结果和以往室内试验结果[13]的对比结果如图4所示。

图4 数值模拟与室内试验对比

由图4可见，数值模拟结果与室内试验呈现高度一致性。在模型B1中，靠近边界的预制裂隙翼型裂纹扩展程度要大于内侧裂隙，即出现明显的“边界效应”，同时，翼型裂纹并不都是从预制裂纹的尖端产生；在模型A4中，多裂纹间的翼型裂纹、反翼型裂纹及剪切裂纹相互搭接，其裂纹扩展模式也与室内试验一致，因此，本文的数值模拟可以准确的反映实际材料的破裂过程及其特征。