气侵初期环空压力瞬态变化规律研究
2022-05-18刘凤和程长坤谯世均吴玉杰杨宏伟
刘凤和,程长坤,谯世均,邢 星,吴玉杰,杨宏伟
1中国石油青海油田分公司 2中国石油青海油田分公司钻采工艺研究院 3中国石油青海油田分公司工程技术处 4中国石油大学(北京)石油工程学院
0 引言
水锤效应是由于流体动量的突然变化而引起的一系列压力交替变化的现象,在油气钻采过程中很常见。但气侵初期的水锤现象在早期气侵的发现中仍然是一个被忽略的问题。
气侵时环空压力的变化通常采用气液两相流模型来模拟,气液两相流模型包括均相流模型、双流体模型和漂移流模型[1-3]。相对于均相流模型和双流体模型,漂移流模型考虑了气液两相之间的滑脱效应以及空隙率、流速沿过流断面的分布规律,使两相流动计算误差显著地降低[4-6],该模型由Zuber和Findlay提出并得到广泛应用[7]。随后很多学者对漂移流模型进行了扩展,并应用其模拟气侵时井筒气液两相瞬态流动问题[8-10],但是漂移流模型无法捕获气侵初期地层气体迅速进入井筒时引起液柱压力的瞬态变化特征。气侵初期,地层气体快速进入井筒使气液交界面之上的钻井液速度突然增加,产生水锤效应。为了准确模拟气侵初期环空压力的瞬态变化规律,考虑了气侵初期的水锤效应,建立了一个水锤—漂移流综合模型来描述气侵过程中环空压力的瞬态变化规律,并采用基于一阶精度的Lax-Friedrichs格式和二阶精度的MacCormack格式的复合差分格式对该模型进行了求解。模型和数值算法的可靠性和准确性通过Wang[11]气侵实验的测量压力数据进行了验证。
利用此模型可以准确地捕获气侵初期井底压力的瞬态变化规律,以期为早期气侵检测提供了理论依据,对发现早期气侵有积极作用,有利于保障井控安全。
1 物理模型
气侵过程中,地层和井筒的整个系统内流体流动状态可以分为三个独立的区域:①地层气体向井筒渗流区域,如图1中的区域1;②气体在环空中向上运移,形成一个气液两相流动区域,如图1中的区域2;③仅包括钻井液的单相流动区域,如图1中的区域3。两相流区域和单相流区域由气液交界面分隔。

图1 气侵时不同区域内流体的瞬态流动图
为建立数学模型准确描述气侵过程中各区域内流体的瞬态流动规律,做出如下的假设:①只考虑沿井筒轴向的一维问题,忽略径向和切向的变化;②直井钻井过程中,气侵发生在井筒底部;③不考虑气体在钻井液中的溶解;④不考虑系统的能量守恒关系,假设井筒中存在一个已知的温度梯度。
2 数学模型
2.1 水锤模型
气侵发生后,气体迅速由地层进入井筒,导致区域3中的泥浆柱速度突然增加,引起水锤效应。区域3中的流体仅由钻井液组成,采用单相流水锤模型来描述气侵初期泥浆柱的水锤效应。
一维经典的水锤模型控制着瞬态管流的场变量随空间和时间的变化,可以由质量守恒方程和动量守恒方程推到得出,气侵时水锤模型的控制方程如下[12-13]:
(1)
(2)
式中:vl—液体流速,m/s;ρl—液体密度,kg/m3;p—环空压力,Pa;f—摩阻系数;d0—井眼直径,m;dp0—钻柱外径,m;θ—井斜角,(°);g—重力加速度,m2/s;a—压力波传播速度,m/s。
2.2 漂移流模型
气侵发生后,气体由地层进入井筒,并在环空内向上运移,形成一个气液两相流区域。气液两相流动过程中主要会发生三种物理现象:相间的质量交换、流体的质量传递和压力波的传播。气液两相流可以采用漂移流模型模拟井筒压力的瞬态变化,其包含了各相的质量守恒关系和混合动量守恒关系。守恒方程的闭合系统是由各相速度间的滑移关系组成。
气相质量守恒方程:
(3)
液相质量守恒方程:
(4)
混合动量守恒方程:
=-ρmgcosθ-Ff
(5)
式中:ρm=αgρg+αlρl;αg—气体的体积分数;αl—液体的体积分数;ρg—气体密度,kg/m3;vg—气体速度,m/s;Гg→l—气相和液相之间的质量交换速率,kg/(m3·s);qsg—气体质量流量,kg/(m3·s);Ff—环空摩阻项,Pa/m。
漂移模型能够准确地描述气相和液相之间的相互作用机理[14],并采用速度分布系数来描述各相流动与整体流动之间的关系。气侵发生时,气体在环空中运移的真实速度表示为:
vg=c0vm+v0
(6)
式中:vm=αgvg+αlvl;c0—分布系数,它描述了气液两相流中速度和体积分数剖面的分布特性;v0—由浮力作用引起的气相滑脱速度,m/s。c0和v0由流型决定,这里采用由Perez提出的模型进行计算。
2.3 地层渗流模型
钻至储层时,如果井底压力低于地层压力,地层中的气体便会侵入井筒。气体由地层侵入井筒符合非达西渗流,可以使用二项式定理计算产气速率[15]。
(7)

(8)
(9)
式中:pe—地层压力,MPa;pwf—井底压力,MPa;qg—气侵速率,m3/d;β—紊流系数;γg—气体比重;rw—裸眼半径,m;re—供给半径,m;h—储层厚度,m;μg—气体黏度,mPa·s;k—地层渗透率,μm2;S—表皮系数。
3 数值解法
3.1 数值格式
水锤模型和漂移流模型的控制方程均表现出一阶线性双曲型方程组的特点[16-17],描述了密度波沿流体流动的下游方向传播和压力波沿流体流动的下游和上游方向传播的物理现象。因此水锤模型和漂移流模型的控制方程可以写成如下紧凑形式:
(10)
式中:w=(αgρg,αlρl,αgρgvg+αlρlvl)T—守恒型参数,是独立物理变量u=(αg,p,vg,vl)T的函数。在水锤模型中,αg=0,vg=0。
利用基于一阶精度的Lax-Friedrichs格式和二阶精度的MacCormack格式的复合差分格式对方程(10)进行求解,该方法是以MacCormack格式为基础,每隔5 000个时间步采用具有数值耗散作用的Lax-Friedrichs格式进行一个时间步长的计算。将长为L的井筒沿轴线方向划分为N个网格,其中zi=z0+iΔz,i=1,2,…,N,Δz=L/N,如图2所示。根据数值求解稳定性的要求,空间步长与时间步长的选取要满足CFL(Courant-Friedrichs-Lewy)条件。
一阶精度的Lax-Friedrichs格式具有如下的守恒形式:
(11)
其中数值通量表示为:
(12)
MacCormack方法是一个三点预测校正的中心差分格式,它的预测步采用向前差分,校正步采用向后差分。预测步的差分格式可表示为:
(13)
校正步的差分格式可表示为:
(14)
其中数值通量可表示为:
(15)
3.2 边界条件处理
气侵发生时,在井底控制体入口处将气侵速率视为已知条件,在井口控制体出口处,将出口压力视为已知条件。由于式(11)~式(15)为三点中心差分格式,无法处理边界条件,因此边界条件需要进行特殊处理。Pauchon和Dhulesia提出可以利用相容性方程对边界条件进行处理[18]。
3.3 求解过程
基于上述数学模型、数值算法以及边界条件,便可以模拟气侵过程中井筒压力的瞬态变化规律,主要的计算流程如图3所示。

图3 主要计算流程图
4 模型验证
利用Wang[11]在全尺寸气侵实验中获得的瞬态压力数据对水锤—漂移流综合模型和数值算法的可靠性和准确性进行验证。该实验包括两口井,其中一口井为实验井,另一口井为储气井。储气井通过一根直径为60.3 mm的管柱向实验井中注气,注气位置为井深600 m处。实验井井眼尺寸为Ø244.5 mm,钻柱外径为127 mm,钻头和PWD工具的井深分别为600 m和580 m,钻井液排量为24 L/s,实验中用水和空气分别代表钻井液和地层气体。
图4为测量压力和模拟压力的分布规律。在实验开始的第75 s开始注气,第200 s停气,注气速度为27 L/s,由图4可知,模拟压力与测量压力的吻合度较好,模拟压力很好的描述了气侵实验中井筒压力的瞬态变化规律。如图5所示,模拟压力相对于实验测量压力的误差均在±10%以内。所以,基于水锤—漂移流综合模型可以准确地预测井筒压力的瞬态变化规律。

图4 测量压力和模拟压力随时间的变化规律

图5 模拟压力相对于测量压力的误差
5 实例分析
利用水锤—漂移流综合模型验证一口柴达木盆地尖北地区实钻井气侵初期的环空压力变化和环空压力对各个影响因素的敏感性。基础参数如下:直井井深4 200 m,水基钻井液的密度为1 200 kg/m3,塑性黏度为15 mPa·s,动切力为9 Pa,水锤模型计算中采用修正幂律模式,气体比重为0.7,钻井液排量为30 L/s,地层压力为54 MPa,渗透率为0.175 μm2,地层供给半径为150 m。
井身结构为:Ø339.7 mm表层套管×1 200 m+Ø244.5 mm技术套管×4 200 m;钻具组合为:Ø215.9 mm PDC钻头+Ø157.5 mm螺杆钻具×9.2 m+Ø157.5 mm钻铤×63 m+Ø127 mm加重钻杆×27 m +Ø127 mm钻杆。
5.1 气侵初期环空压力变化分析
图6为井底发生气侵时,气侵速率随时间的瞬态变化规律。由图6可知,气侵发生后,地层气体开始会以较大的加速度迅速进入井筒,在ts时刻气侵速度达到拟稳定状态,之后气侵速度随着井底压力的降低逐渐升高。将开始发生气侵到ts时刻的时间间隔定义为瞬态气侵时间,将ts时刻的气侵速率定义为瞬态气侵速率。

图6 气侵速率随时间的瞬态变化曲线
图7为气侵初期井深4 170 m处环空压力随时间的瞬态变化规律。由图7可知,气侵发生后,地层气体迅速进入井筒导致泥浆柱速度突然增加,引起水锤现象,水锤压力迅速增加并随时间呈周期性波动;水锤压力的振幅随时间逐渐减小,且第一个(即最大的)波峰发生在瞬态气侵时间ts之后;一段时间后,环空压力开始随时间近似线性降低,这是因为气液交界面上升至4 170 m处,该处的部分钻井液被气体代替形成气液两相流区域,从而导致该处环空压力降低。

图7 井深4 170 m处环空压力随时间的瞬态变化曲线
图8为不同井深处气侵初期的环空压力与正常钻进时相应位置处环空压力的比值,将此比值定义为相对环空压力比。气侵初期气液交界面以上不同井深处相对环空压力比近似相等;随着井深的减小,气液交界面上升至相应位置的时间增加,因此环空压力开始降低的时间也增加,这可以作为气液交界面位置追踪的依据,且不同时间段内不同井深处相对环空压力比之间的一致性和差异性为多测点早期气侵识别提供了理论依据。
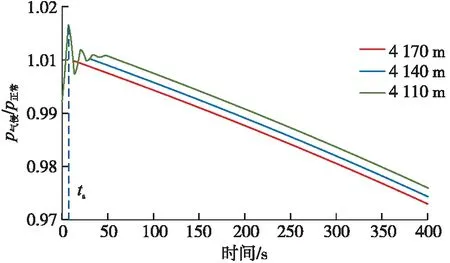
图8 不同井深处气侵初期与正常钻进时相应位置处的环空压力比
5.2 气侵初期井底压力敏感性分析
图9为当瞬态气侵时间为7 s时,井深4 170 m处不同瞬态气侵速率条件下的环空压力瞬态变化曲线。由图9可知,气液交界面上升至4 170 m之前,瞬态气侵速率越大,水锤效应越明显,水锤压力波动振幅越大,水锤压力增量越大,气液交界面上升至该位置的时间越短,但瞬态气侵速率对水锤压力的波动频率几乎没有影响。当气液交界面上升超过4 170 m后,该处环空压力受漂移流模型控制,随着瞬态气侵速率的增加,环空压力的下降速度增大。

图9 不同瞬态气侵速率条件下的环空压力瞬态变化曲线
图10为当瞬态气侵速率为15 L/s时,井深4 170 m处不同瞬态气侵时间条件下的环空压力瞬态变化曲线。由图10可知,气液交界面上升至4 170 m之前,随着瞬态气侵时间的减小,水锤效应更加明显,水锤压力波动振幅和波动频率均增大,但气液交界面上升至该位置的时间几乎相同;当气液交界面上升超过4 170 m后,不同瞬态气侵时间条件下的环空压力均相等,且下降速率也相同。所以瞬态气侵时间仅对气侵初期的水锤效应有较大的影响,但对于两相流区域内的环空压力变化几乎没有影响。

图10 不同瞬态气侵时间条件下的环空压力瞬态变化曲线
图11~图13分别为气侵初期井深4 170 m处不同地层渗透率、井底负压差(地层压力减井底压力)和井眼尺寸条件下的环空压力瞬态变化曲线。气侵初期环空压力受地层渗透率、井底负压差和井眼尺寸的影响较大,且随着地层渗透率和井底负压差的增加,以及井眼尺寸的减小,水锤现象更加显著,水锤压力波动振幅增加,水锤压力增量也增大,气液交界面上升至该位置的时间减少,但水锤压力波动频率基本一致。随着地层渗透率和井底负压差的增加,及井眼尺寸的减小,瞬态气侵速率增加而瞬态气侵时间变化较小综合作用所导致的结果,见表1。当气液交界面向上运移超过4 170 m后,随着地层渗透率和井底负压差的增加,以及井眼尺寸的减小,该处的环空压力下降速度增大。

图11 不同地层渗透率条件下环空压力随时间的变化曲线

图12 不同井底负压差条件下环空压力随时间的变化曲线

图13 不同井眼尺寸条件下环空压力随时间的变化曲线

表1 不同敏感性参数条件下的瞬态气侵速率和瞬态气侵时间
6 结论
(1)考虑了气侵初期的水锤效应,建立了水锤—漂移流综合模型来描述气侵过程中环空压力的瞬态变化规律,并提出采用基于Lax-Friedrichs格式和MacCormack格式的复合差分格式对该模型进行了求解。
(2)气侵发生初期,由于地层气体迅速进入井筒导致钻井液柱产生水锤效应,气液交界面以上钻井液柱的环空压力增加并随时间周期性波动,波动振幅随时间逐渐减小;气液交界面以下的两相流区域内的环空压力随时间近似线性降低。
(3)水锤压力波动振幅随瞬态气侵速率的增加和瞬态气侵时间的减少而增大,而波动频率仅随瞬态气侵时间的减少而增大。地层渗透率、井底负压差越大,井眼尺寸越小,则瞬态气侵速率越大,气侵初期的水锤效应越显著,且两相流区域内的井底压力下降速度越快。
(4)从尖北地区一口实钻井来看,气侵初期气液交界面以上不同井深处的相对环空压力比近似相等,且随着井深的减小,气液交界面上升至相应位置的时间增加,因此环空压力开始降低的时间也增加。这可以作为气液交界面位置追踪的依据,且不同时间段内不同井深处的相对环空压力比之间的一致性和差异性为多测点早期气侵检测提供了理论依据。
