基于相场法的井壁微裂缝扩展规律及坍塌机理研究
2022-05-18韩梦天贾利春廖智海史彪彬
赵 宁,尹 飞,韩梦天,贾利春,廖智海,史彪彬
1成都理工大学能源学院 2北京自动化控制设备研究所 3中国石油川庆钻探工程公司钻采工程技术研究院
0 引言
随着非常规及深层油气资源的勘探开发力度的增加,钻井过程中井壁失稳带来的影响日益突出,尤其在裂缝性地层中由于裂缝的存在降低了岩石强度,当井壁应力差较大或钻井液侵入造成裂缝扩展和连通,引起大面积的井壁坍塌掉块,阻碍了安全钻井。例如,在顺北油气田5号断裂带深层油气勘探开发过程中,多口井发生了破碎性碳酸盐岩井壁坍塌,严重阻卡的5口井的钻井周期共延长了913 d[1];川西多口油气井在钻遇马鞍塘—雷口坡组碳酸盐岩地层时也发生了不同程度的井壁坍塌和掉块,严重影响钻井进度和井下安全[2]。
由于裂缝发育对井壁稳定性的影响非常显著,诸多学者对此展开了研究。陈卓等[3]在建立硬脆性泥页岩的损伤本构模型的基础上,发现泥页岩裂缝发育程度对井壁稳定影响最大。张艳娜等[4]分析了裂缝发育对碳酸盐岩孔渗特性、力学强度的影响,发现诱发井壁垮塌的主导因素是裂缝间力学弱面效应突出。刘志远等[5]对裂缝性井壁失稳的影响因素进行了分析,发现裂缝倾角与岩石的强度直接相关,有裂缝情况下的水化作用将更加明显。常见关于裂缝扩展的数值模拟方法包括位移不连续法(DDM)[6]、扩展有限元法(XFEM)[7]和离散元法(DEM)[8]等。何雅文[9]通过扩展有限元的方法研究了井壁在受压应力作用下的裂缝扩展规律,裂缝没有发生分叉或相交,只在井壁上分别产生了两条不相交的裂缝,体现了扩展有限元法难以处理复杂裂缝扩展模拟的局限性。王晓阳[10]通过数值模拟的方法,研究了井周应力差作用下井壁剪切破坏区域,但无法体现裂缝扩展形态与破坏程度。位移不连续法(DDM)、扩展有限元法(XFEM)和离散元法(DEM)等数值模拟中只是将裂缝作为突变型界面存在,难以处理复杂的裂缝扩展问题。
现有研究难以刻画井壁微裂缝扩展过程及形态,不能准确预测裂缝性地层井壁坍塌压力,本文针对该问题进行了深入研究,提出了基于相场法的井壁微裂缝扩展模型。相场法通过相场变量来描述材料基质与裂缝之间的平滑过度,裂缝可以随着相场变量的演化自发的扩展,能够模拟裂缝的相交、分叉和三维扩展等复杂形态[11-12]。然后,利用相场法模拟了井壁微裂缝扩展的动态过程;分析了钻井液液柱压力和天然裂缝等因素对微裂缝扩展的影响规律,并对预测的坍塌压力进行对比分析和验证。
1 相场法表征裂缝
1.1 相场和裂缝表面函数
相场法认为岩石在受外力作用下产生的弹性能造成了岩石的损伤,当弹性能超过岩石破坏所需的临界能量时,岩石就会完全破坏形成裂缝[11]。
如图1所示,假设存在一个截面积为Γ、轴向长度为L的杆,则长杆所占据的区域为B=Γ×L,在杆的轴向坐标x=0处有一个物理裂缝。
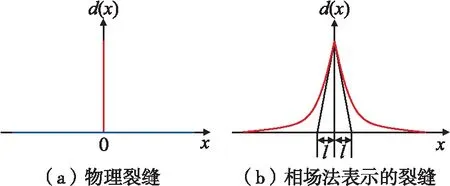
图1 裂缝拓扑示意图
对于一维问题,相场法通常采用式(1)的形式来表示裂缝[13],式中d(x)∈[0,1],0表示未破坏,1表示完全破坏形成裂缝。相场法将裂缝看作是一个扩散型的损伤带,其宽度主要由相场长度尺度l来控制,l越趋近于0,裂缝形态就越接近真实物理裂缝[14]。
(1)
对于多维问题,n维固体模型所在域为B,B⊂Rn,n∈[1,2,3],边界∂B⊂Rn-1。此时的裂缝表面Γ为三维问题的曲面或二维问题的曲线,见图2。
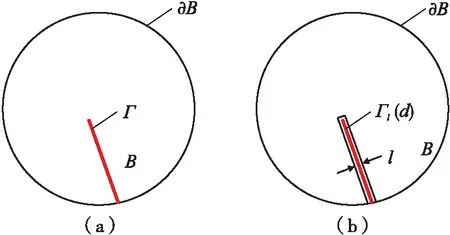
图2 裂缝模型图
相场d(x)随时间的变化为d(x,t),通过裂缝表面函数Γl(d)来描述裂缝[15]:
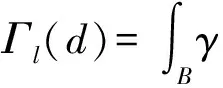
(2)
式中:γ(d,∇d)—裂缝表面密度函数。
由式(2)欧拉变分形式可得域B中服从Dirichlet边界条件的裂缝相场为:
(3)
1.2 自由能函数
在固体模型所在的域B内,各向同性固体的位移场为r(x,t),固体在域B内受位移r和相场d影响的弹性能We为[16]:
(4)
其中w(ε,d)为弹性能密度:
w(ε,d)=[g(d)+k]w0(ε)
(5)
衰减函数g(d)=(1-d)2来描述裂缝演化引起的能量衰减,只对拉应变张量作用。g(0)=1时,表示岩石未发生破坏;g(1)=0时,表示岩石完全破坏产生裂缝,而k是一个极小的正值,它的存在是为了保证模型的稳定性。w0(ε)是标准的自由能密度函数。
在裂缝的演化过程中,由于只有在拉伸的时候才会产生裂缝并释放能量,因此要将应变张量分解为反映拉应力的正应变张量ε+和反映压应力的负应变张量ε-[15]:
ε=ε++ε-
(6)
在对应变张量分解后,可获得裂缝扩展的本构自由能函数W(ε,d)[17]:
(7)
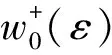
1.3 裂缝扩展耗散函数与相场演化方程
单位面积裂缝扩展所需要的能量定义为临界能量释放率Gc[18],表征裂缝扩展过程中受到的阻力。由此可知面积为Γl(d)的裂缝扩展所需能量为[19]:
(8)
结合断裂变分理论[20],可得到在弹性应变能驱动下的相场演化方程[12]:
(9)
为了能正确反映加卸载情况下的裂缝扩展规律,使用与应变有关的应变历史函数H(x,t)来保证相场d不会逆向发展,结合式(9)即可得到裂缝扩展的控制方程[15]:
(10)
1.4 有限元离散
对相场微分方程和位移进行有限元离散,由裂缝扩展的控制方程可得到相应加载步的计算形式[15]和位移场的弱形式[16],如式(11)所示:
(11)
式中:Hn=H(rn)—上一次载荷增量得到;δd—虚损伤分布函数;δr—虚位移函数;ft—固体受到的体积力;fm—边界∂B上受到的表面力。
本文研究的是二维问题,采用三角形等参数单元对相场函数、相场梯度场以及位移函数和位移变分函数近似表示,然后得到相场d的线性方程组[15]以及位移场r的支配方程[16]如下:
(12)
式中:Kd、K1+K2—总体刚度矩阵;Fd、Fn+1—总体节点载荷矩阵。
在相场法裂缝扩展演化过程中,外力做功形成的总能量一部化为形成新裂缝所需要的裂缝表面能Wc(d);另一部分则会转化为储存在岩石内的自由能W(ε,d),即弹性应变能。其中正应变能会随着裂缝的扩展而耗散,裂缝扩展的方向、长度以及何时扩展等扩展机制与位移场r和相场d等相关。
2 有限元模型
根据弹性力学理论,可把三维井壁力学分析简化为平面应变问题。井壁力学模型如图3所示,井壁承受最大水平地应力、最小水平地应力和钻井液液柱压力。
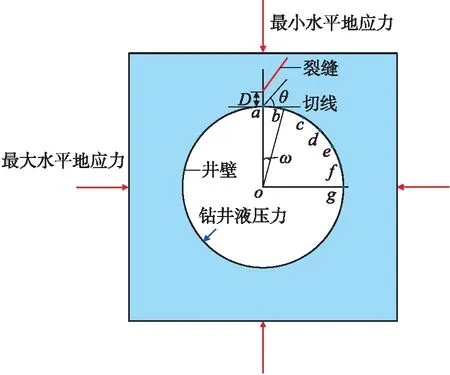
图3 井壁力学模型示意图
考虑井壁含天然裂缝的情形,在第一象限范围内以15°为间隔划分了a~g共7个井壁节点;天然裂缝和井壁节点切线的夹角为θ;天然裂缝端点与井壁的距离为D,当D=0时,表示天然裂缝与井壁连通。
本文采用相场法模拟钻开井眼后井壁产生的微裂缝(以下简称微裂缝)扩展过程,通过显式有限元对相场法表征的裂缝进行求解,因此需要在有限元软件中设置相场法表征裂缝扩展的关键参数和岩石本体的强度参数,相场法表征裂缝的主要参数包括长度尺度和临界能量释放率,长度尺度控制扩散型损伤带的宽度,临界能量释放率体现单位面积裂缝扩展所需的能量。模型中选取长度尺度为0.046 mm,岩石基质与天然裂缝的临界能量释放率分别为130 J/m2和65 J/m2。建立井壁微裂缝扩展的有限元模型,如图4所示。模型中井眼直径为241.3 mm;为了消除边界效应,正方形地层的边长取井眼直径的10倍;天然裂缝的缝宽取0.02 mm。在地层边界上施加最大、最小水平地应力,首先使地层达到地应力场平衡;然后模拟钻穿井眼,并在井壁上施加钻井液液柱压力。由于相场长度尺度较小,为提高裂缝扩展的模拟精度,对井壁网格进行局部加密,最大单元尺寸为0.023 mm,最大单元增长率为1.2。
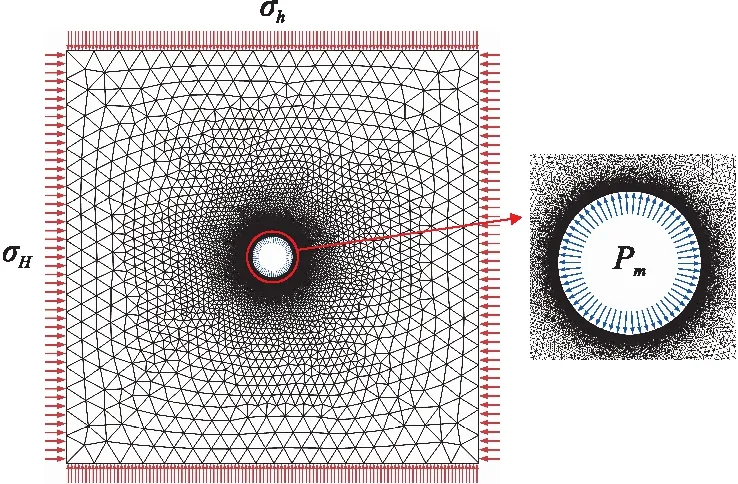
图4 井壁微裂缝扩展的有限元模型
设碳酸盐岩地层的基质为各向同性的线弹性介质,天然裂缝为填充缝,忽略渗流和裂缝内流体压力变化的影响。在把相场微分方程及位移场进行有限元离散后,通过显式有限元软件进行求解,设置材料参数、边界条件;然后加载应力场,逐步计算位移场和相场;分析不同压力或天然裂缝情况下井壁微裂缝演化。相场法认为当损伤d=1时,岩石完全破坏而后形成裂缝;如果在一定钻井液液柱压力下井壁经过一段时间后损伤保持初始值不变,则井壁上不产生微裂缝,认为井壁保持稳定状态,这个临界钻井液液柱压力作为井壁坍塌压力。模型的主要参数[21]详见表1。
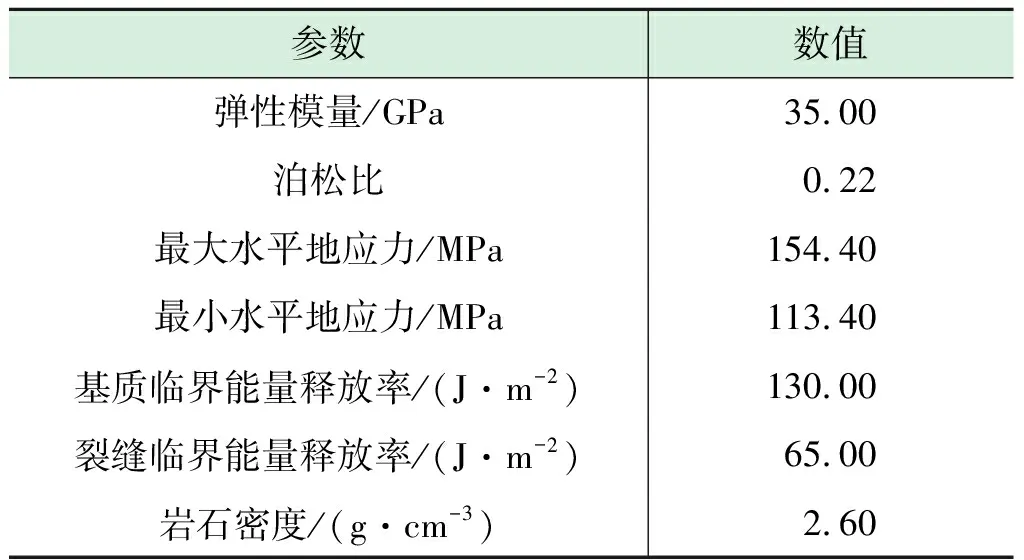
表1 模型的主要参数
3 井壁失稳规律分析
以四川盆地某区块碳酸盐岩地层某井为例[21],在钻至井深6 239 m后按设计调钻井液密度到1.30 g/cm3,尝试钻进2 m发生了卡钻。分析原因是该层位地层完整性较差、天然裂缝发育,实际井壁坍塌压力比预测值高,使用的钻井液液柱压力不足以支撑井壁稳定。采用井壁微裂缝扩展模型,揭示微裂缝扩展过程及井壁坍塌机理。
3.1 钻井液液柱压力对井壁稳定性的影响
钻开井眼后,井壁由岩石支撑转变为钻井液支撑,钻井液液柱压力大小会影响井壁微裂缝的扩展。钻井液液柱压力依次选取73.5 MPa、75.5 MPa、77.2 MPa、79.2 MPa、80 MPa,分析钻井液液柱压力对井壁微裂缝扩展的影响规律。不同钻井液液柱压力下井壁微裂缝扩展形态如图5所示,影响规律如表2所示。
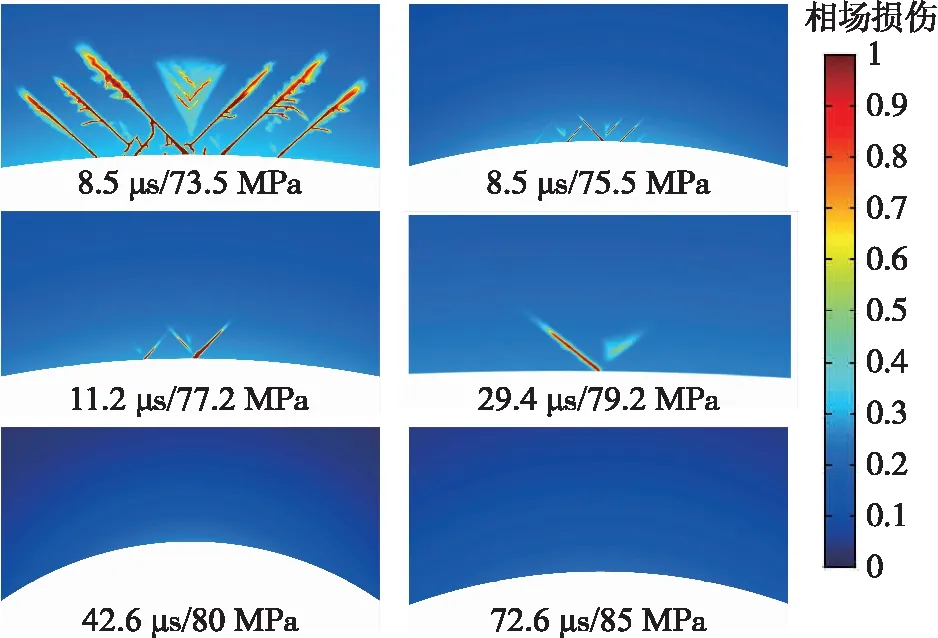
图5 井壁微裂缝扩展的演化过程图
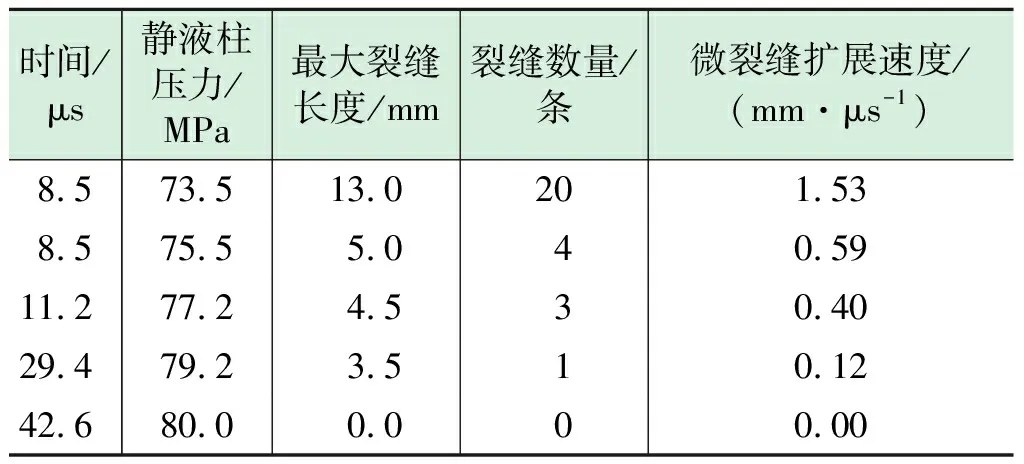
表2 钻井液液柱压力对微裂缝扩展的影响规律表
可知,随着钻井液液柱压力增大(趋近于坍塌压力),井壁上产生的微裂缝数量减少、缝长变短、微裂缝扩展速度降低;当钻井液液柱压力达到80 MPa时,42.6 μs时井壁上最大损伤仍然维持在初始损伤0.27,井壁不会萌生微裂缝,说明井壁能够保持稳定,此时的钻井液液柱压力即为不含天然裂缝的井壁坍塌压力。
3.2 井壁微裂缝扩展模拟
首先,分析在地层不含天然裂缝且钻井液支撑不足情况下井壁微裂缝扩展的演化过程。经模拟,在钻井液液柱压力为73.5 MPa的条件下,井壁微裂缝扩展的演化过程如图6所示。可知,4.7 μs时井壁上开始萌生微裂缝,相场损伤d增大到0.92;6.0 μs时井壁上产生了7条微裂缝,相场损伤d增大到1.0,并维持在1.0;6.0~6.6 μs时微裂缝呈现交错生长,且微裂缝走向发生偏转;8.2 μs时主裂缝上又生成了新的分支裂缝,微裂缝的数量大量增加,更多的微裂缝出现连通。井壁上微裂缝的扩展及连通可能引起井壁坍塌或掉块。
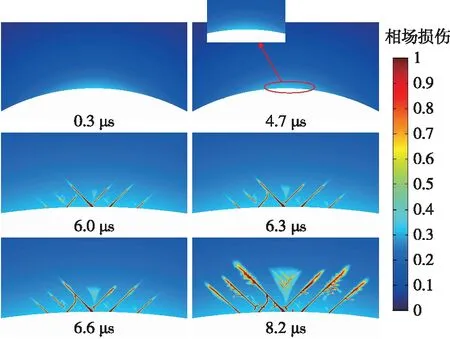
图6 不同钻井液液柱压力下井壁微裂缝形态图
3.3 天然裂缝对井壁稳定性的影响
考虑地层发育天然裂缝的情形,有必要分析天然裂缝对井壁稳定的影响。设置天然裂缝位于图3中井壁a点、与井壁切线夹角45°、与井壁距离2 mm,缝长为3 mm。在钻井液液柱压力为85 MPa的条件下,含天然裂缝井壁的微裂缝扩展演化过程如图7所示。由图7可知,微裂缝沿着天然裂缝向两侧扩展,且优先向井壁方向延伸;1.8 μs时裂缝与井壁连通,形成了一条约9 mm长的微裂缝,微裂缝扩展速度为5 mm/μs,扩展速度更大。

图7 含天然裂缝井壁微裂缝扩展演化图
在天然裂缝与井壁相交且钻井液液柱压力为90 MPa条件下,天然裂缝的位置和角度对微裂缝初始损伤的影响如图8所示。位于最小水平地应力方位(a点)的天然裂缝初始相场损伤比其他位置大,在e点、f点、g点趋近于0;随着天然裂缝与井壁切线的夹角增大,微裂缝初始损伤先增大后减小,并在夹角45°时达到极大值。进一步分析天然裂缝与井壁的距离对裂缝初始损伤的影响规律,如图9所示,随着天然裂缝与井壁的距离减小,裂缝初始损伤逐渐增大;随着井壁节点逐渐远离a点,初始损伤逐渐减小,e点后趋近于0。综上可知,当天然裂缝位于最小水平地应力方位、夹角45°且与井壁连通(以下称为最危险天然裂缝产状)时,微裂缝容易起裂和扩展,此处井壁坍塌失稳风险最大。
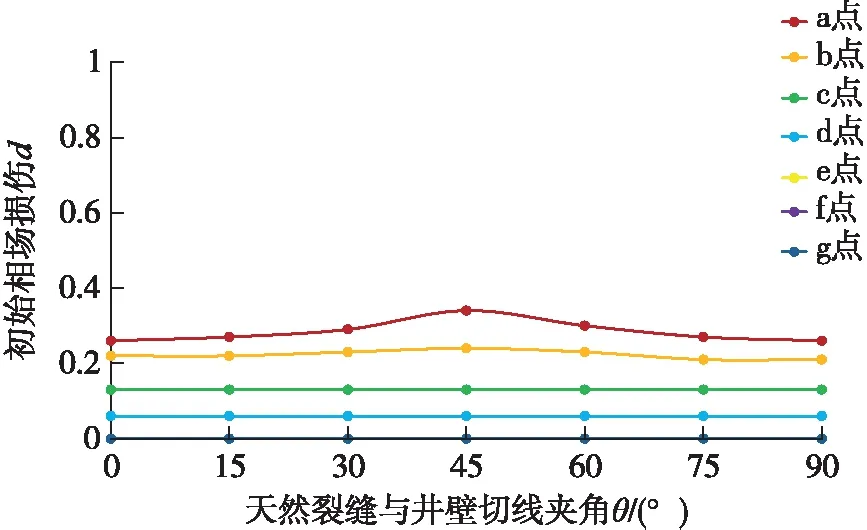
图8 天然裂缝位置及角度对裂缝初始相场损伤的影响
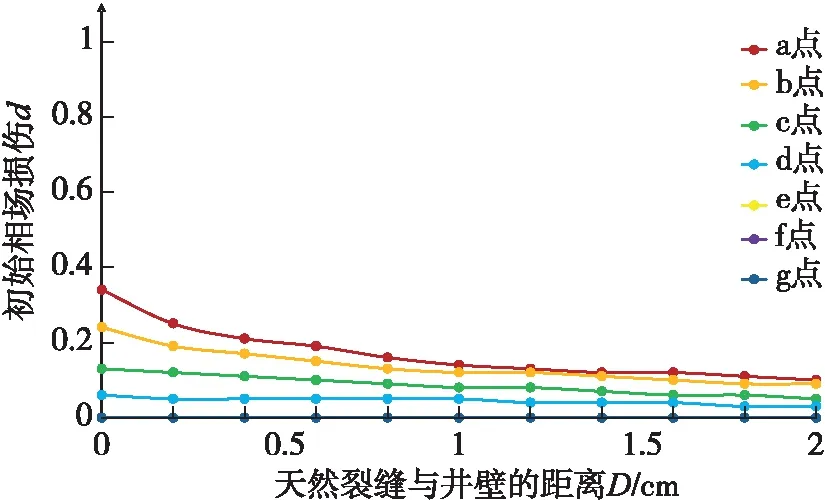
图9 天然裂缝与井壁的距离对裂缝初始相场损伤的影响
在最危险天然裂缝产状下,分析钻井液液柱压力对天然裂缝起裂时间的影响,如图10所示。可知,随着钻井液液柱压力增加,天然裂缝起裂时间增大,当钻井液液柱压力达到93.7 MPa时,天然裂缝的起裂时间趋近于无穷大,说明此时井壁维持稳定。综上,在最危险天然裂缝产状下井壁的坍塌压力为93.7 MPa,上文指出不含天然裂缝井壁的坍塌压力为80 MPa,天然裂缝使井壁坍塌压力增大了17.1%。因为天然裂缝起裂较岩石基质破坏所需能量更低、微裂缝扩展速度更大,需要更高的钻井液液柱压力维持其力学平衡和阻止微裂缝起裂。
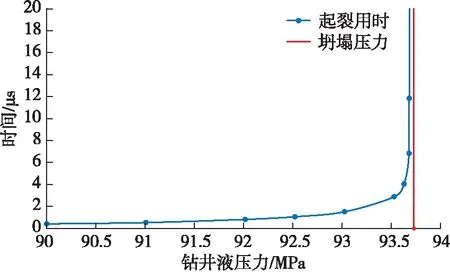
图10 不同钻井液液柱压力下天然裂缝起裂时间
3.4 模拟效果分析
在上述案例中,针对地层不含天然裂缝的井段,模型预测的坍塌压力当量密度为1.30 g/cm3;地层含天然裂缝的井段,模型模拟得到在最危险天然裂缝产状下井壁坍塌压力当量密度为1.52 g/cm3;随机裂缝下井壁坍塌压力当量密度范围应为1.30~1.52 g/cm3,平均值为1.41 g/cm3,现场使用密度为1.30 g/cm3的钻井液钻进时发生卡钻,说明此处具有天然裂缝,在此产状下需要采用更高密度的钻井液方能抑制井壁坍塌。
4 结论
(1)基于相场法的井壁微裂缝扩展模型能够模拟井壁微裂缝萌生、扩展、分支缝产生和交叉贯通的扩展过程,可直观反映裂缝性地层钻井井壁失稳的机理,指导修正坍塌压力设计。
(2)数值模拟表明,随着钻井液液柱压力逐渐趋近坍塌压力,井壁上产生的微裂缝数量减少、缝长变短、扩展速度降低;当天然裂缝位于最小水平地应力方位、夹角45°且与井壁连通时,微裂缝最容易起裂和扩展,此处井壁坍塌失稳风险最大。
(3)因为天然裂缝处的起裂较岩石基质破坏所需能量更低、微裂缝扩展速度更大,所以需要更高的钻井液液柱压力维持其力学平衡和阻止微裂缝起裂。案例中天然裂缝使井壁坍塌压力增大了17.1%,当井壁不起裂时临界钻井液液柱压力可作为裂缝性地层坍塌压力的修正值。
