基于飞蛾扑火优化的MCKD算法在往复压缩机轴承故障诊断中的应用
2022-05-18王金东李云峰赵海洋李彦阳
王金东,李云峰,赵海洋,李彦阳
(东北石油大学机械科学与工程学院,黑龙江 大庆 163318)
1 引言
往复压缩机广泛应用于石油化工领域,作为一种高噪声设备,其振动信号存在大量噪声干扰。当往复压缩机轴承间隙过大时,故障信息容易淹没在强背景噪声中,其振动信号具有非线性、非平稳性。故研究高效、实用的往复压缩机故障诊断与监测方法意义重大。
最小熵解卷积(MinimumEntropy Deconvolution,MED)使用的峭度对瞬态脉冲很敏感,不能很好地反映周期性冲击,当故障冲击特征完全淹没在背景噪声中,该方法提取故障信息的效果变差[1]。最大相关峭度解卷积(Maximum Correlated Kurtosis Deconvolution,MCKD)能充分利用故障的周期性特征,以相关峭度为指标,利用解卷积信号相关峭度的最大值为判据,迭代选择出最佳滤波系数[2]。然而,MCKD方法中的故障周期T、滤波器长度L等参数需要凭借人为经验选取[3],影响降噪效果。在往复压缩机工作过程中,由于负载、压力等因素的变化,会引起往复压缩机的瞬时转速的改变,从而造成往复压缩机轴承理论故障频率与实际故障频率不吻合。针对MCKD方法的局限性,本文采用飞蛾扑火优化算法对MCKD参数故障周期T和滤波器长度L进行优化,并将该方法应用于往复压缩机轴承故障的诊断,实现了故障特征的准确提取。
由于熵值分析能表征振动信号的复杂性,被广泛应用于机械的故障诊断领域。多尺度熵(Multiscale Entropy,MSE)用来描述多个尺度上时间序列的复杂度。通过粗粒化过程得到多个尺度时间序列,可以在每个尺度上进行分析,能更好地反映时间序列的复杂性和规律性。往复压缩机轴承故障振动特征复杂程度在不同尺度下表现出一定的差异性,在多尺度下提取信号的熵值可以提高特征向量的准确性。
本文提出一种基于飞蛾扑火优化的MCKD往复压缩机轴承故障诊断方法。引入飞蛾扑火优化算法解决MCKD参数选择问题,利用参数优化后的最大相关峭度解卷积算法提取轴承振动信号中的冲击成分。采用多尺度熵对解卷积后的信号量化分析,用熵值来构建轴承故障的特征向量,并将特征向量输入到极限学习机对故障特征进行分类识别。
2 改进的最大相关峭度解卷积算法
2.1 MCKD算法原理
MCKD算法的原理是通过最大化相关峭度来获得最优滤波器系数f,即
(1)
式中y——解卷积处理后的信号
xn——原始信号
L——滤波器长度
相关峭度CKM(T)的定义为
(2)
式中N——数据长度
T——故障信号的周期
M——位移数
当CKM(T)值取最大值时,求得此时滤波器系数f,即
(3)
得
(4)
其中
将得到的最优滤波器系数带入公式(1)中即可得到故障信号y。
2.2 基尼指数
基尼指数(Gini Index,GI)是经济学中描述财富不平等的指标,最近被用于机械故障诊断领域。文献[4]研究表明,GI被用来检测信号中的冲击特性,是一种有效的指标。GI的值在[0,1]的范围内,且GI值越大,表明信号中包含越多的故障信息。GI的计算公式如下
(5)
xl1是x的l1范数;|x[k]|是对时间序列x=[x(1),x(2),…,x(n)]中的元素重新排序,并表示为|x[1]|≤|x[2]|≤,…,|x[N]|。
2.3 MCKD参数优化
MCKD进行信号处理时,需凭经验设置故障周期T和滤波器长度L,当参数选取不当时,会造成误诊,这使得MCKD算法在实际应用中有一定的局限性。飞蛾扑火优化算法(Moth-flame Optimization,MFO)结构简单、参数较少、寻优能力强[5],可对MCKD的参数进行优化。利用GI作为适应度函数,当GI值达到最大时,飞蛾扑火优化算法停止迭代,输出最佳的参数组合。
在MFO算法中,飞蛾是求解问题的候选解,式(6)代表飞蛾个体的空间位置,式(7)表示飞蛾个体对应的适应度值。
(6)
OM=[OM1OM2…OMn]T
(7)
式中n——飞蛾的数量
d——变量的维数
用式(8)代表火焰初始位置,与飞蛾的位置具有相同维度的变量矩阵。并用式(9)存储各火焰的适应度值。
(8)
OF=[OF1OF2…OFn]T
(9)
(10)
式中Dij=|Fi-Mi|——第j个火焰到第只飞蛾的距离
b——螺旋形状常数
t——随机数,其取值范围在[-1,1]之间,t决定了下一个飞蛾个体距离火焰的远近程度
火焰位置由飞蛾每次更新产生,并在迭代过程中,根据火焰适应度值的大小去掉适应度值不佳的火焰,能够很好的协调全局搜索和局部搜索。公式(11)表示剩余火焰数量在迭代过程中的变化。
(11)
式中N——最大火焰数量
T——最大迭代次数
l——当前迭代次数
2.4 仿真信号验证
构造的仿真信号组成如下:模拟故障周期冲击信号如式(12)所示,固有频率Wn设为3000 Hz,阻尼系数ξ设为0.05,位移常数y0为1.8,冲击周期T为0.018 s,故障频率为55.6 Hz;模拟谐波干扰信号,添加幅值为0.5,频率分别为22.5 Hz、50 Hz和70 Hz的正弦信号,如式(13)所示;为模拟实测振动信号中的噪声,加入高斯白噪声信号如式(14)所示。将三类信号合成为仿真信号,如式(15)所示。仿真信号的时域波形和包络谱如图1、2所示。
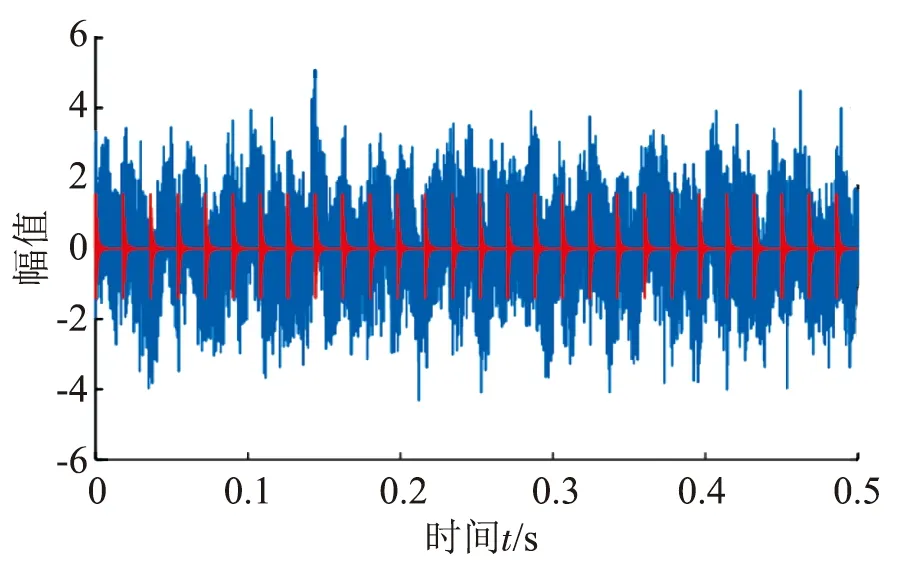
图1 仿真信号时域波形
(12)
x2(t)=0.5sin(πnit)
(13)
x3(t)=wgn(1,N,0.3)
(14)
x(t)=x1(t)+x2(t)+x3(t)
(15)
ni分别为40、100、140;仿真信号的采样频率fs=20 kHz;采样时间t=0.5 s;N为数据长度。
经过参数优化后,得到的最优参数组合为[L,T]=[83,354],带入MCKD,对仿真信号进行解卷积处理,其时域图如图3所示,在图中可明显看出故障的冲击特征。图4为解卷积处理后的信号包络谱,可以看出故障特征频率54.9 Hz与理论故障频率基本一致,可见该方法可实现故障特征的准确提取。
为了对比分析,采用原MCKD对仿真信号进行解卷积处理,按照经验输入参数[L,T]=[30,360],得到的时域图如图5所示,相较于提出的飞蛾扑火优化的MCKD方法,其提取结果中噪声干扰成分较多。图6为解卷积处理后的信号包络谱,可以看出故障特征频率的幅值要小于文中提出方法的故障特征频率幅值。

图2 仿真信号包络谱图
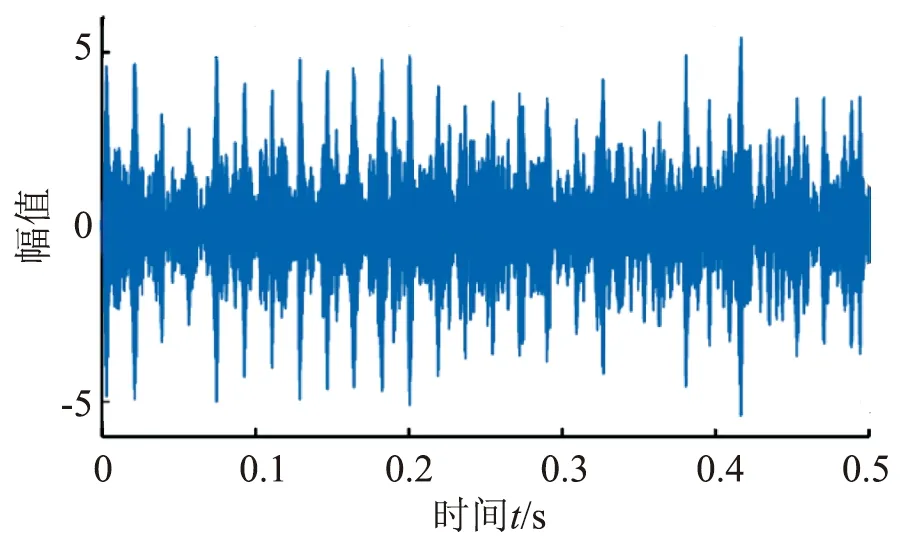
图3 仿真信号经MCKD处理后的时域波形
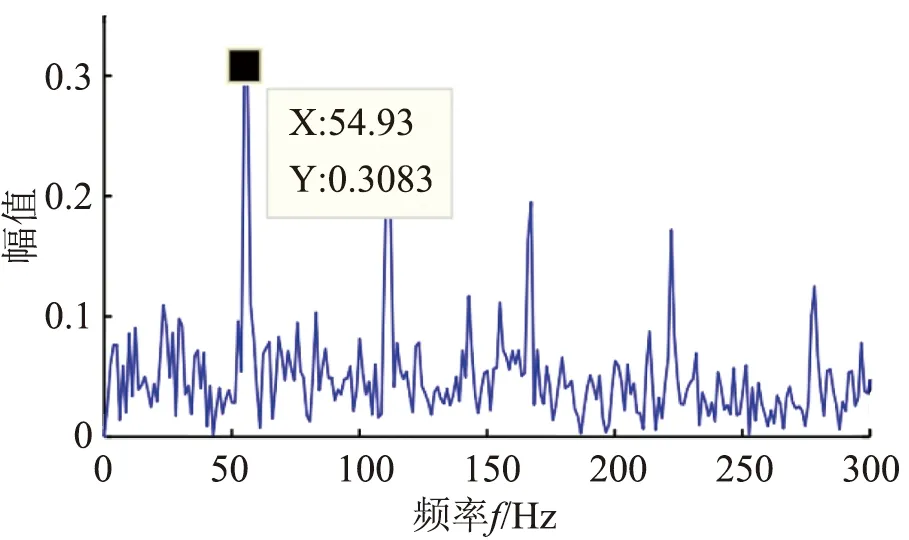
图4 仿真信号经MCKD处理后的包络谱图
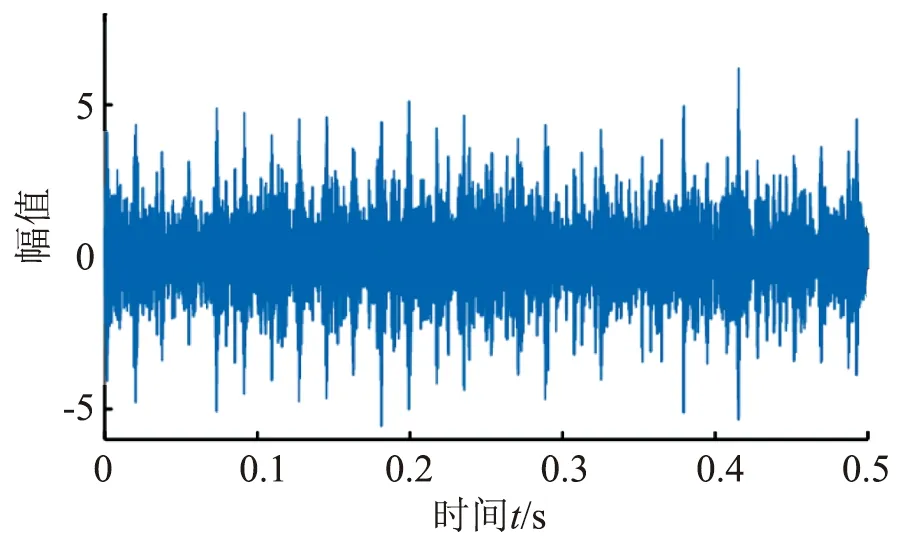
图5 仿真信号经原MCKD处理后的时域波形
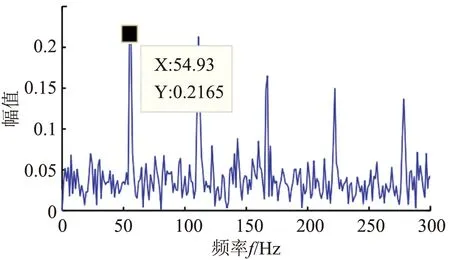
图6 仿真信号经原MCKD处理后的包络谱图
3 多尺度熵
多尺度熵(MSE)最早被用于量化生物医学时间序列的复杂性,后被广泛应用于机械故障诊断领域。其MSE的计算步骤如下
(1)粗粒化原始序列Xi={x1,x2,…,xN},并获得不同时间尺度的新序列为
(16)
式中N——数据长度
τ——尺度因子
(2)利用嵌入维数将原始序列重组为m维向量:Xm(1),Xm(2),…,Xm(N-m+1),其中Xm(i)的表达式为
Xm(i)=[xi,xi+1,L,xi+m+1]
(17)
式中i=1,2,L,N-m
(3)计算向量Xm(i)与向量Xm(j)之间的距离,即
(18)
式中i,j=1,2,…,N-m,i≠j

(19)
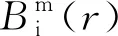
(20)
(6)将时间序列重组为m+1维向量,重复上述过程,得到Bm+1(r),表达式为
(21)
(7)则样本熵被定义如下
(22)
(8)计算每个尺度相对应序列的样本熵值,得到MSE:即
MSE(τ)=SampEn(τ,m,r,N)
(23)
4 往复压缩机轴承故障诊断
4.1 实测信号故障特征提取
本文的试验数据来源于所在实验室完成的2D12-70型往复压缩机现场模拟故障试验。在试验中,模拟了一级连杆大、小头轴承间隙故障,二级连杆大、小头轴承间隙故障。该压缩机电动机转速和采样频率分别为496 r/min和50 kHz。加速度传感器设置在十字头下方。
本文选取0.4 s时间段的压缩机振动数据进行分析,一级连杆小头轴承间隙大故障的时域波形如图7所示。在往复压缩一个工作循环中,轴瓦受到两次冲击,由于往复压缩机反向角的存在,造成这2次冲击的时间不相等[7,8],因此,故障周期T设置为往复压缩机一个工作循环的周期。根据MCKD算法原理,移位数取1,设置参数L的取值范围为:10~100,T的取值范围为:5940~6185。利用飞蛾扑火优化算法来确定MCKD的滤波器长度L和故障周期T,可得最佳优化参数组合[L,T]=[30,6033]。将参数输入到MCKD算法中,对轴承信号进行解卷积处理,并得到经过MCKD处理后的一级连杆小头轴承间隙大故障的时域波形如图8所示。
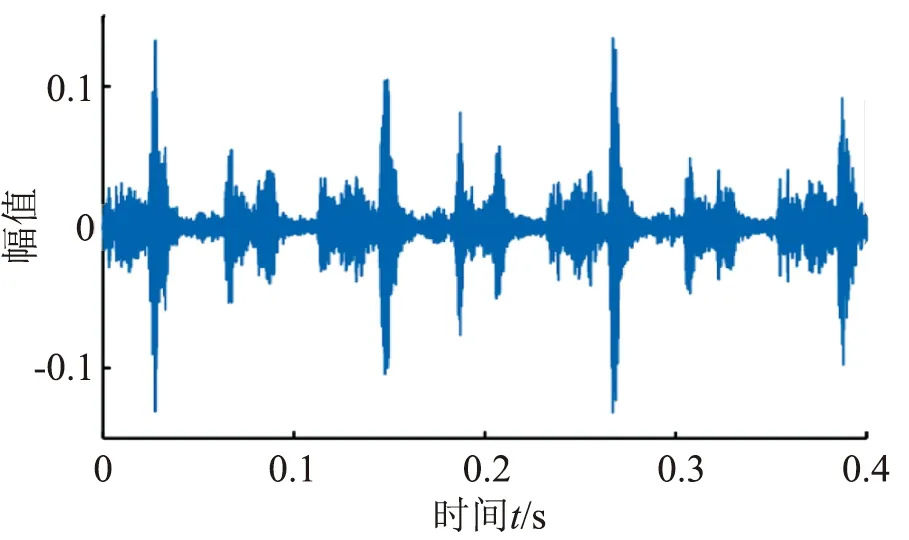
图8 经MCKD解卷积处理后时域波形图
采用相同的方法,分别对一级连杆大、小头轴承间隙故障,二级连杆大、小头轴承间隙故障,以及正常状态下的振动信号进行处理,计算这5种状态经MCKD处理的振动信号的多尺度熵。设置嵌入维数m=2,相似容限r=0.15 SD,尺度因子τ=20,得到轴承5种状态MSE的曲线图如图9所示。由图可见,5种轴承状态下的MSE熵值在尺度因子τ=2~8之间具有较好的可分性。因此,选取每种状态振动信号的MSE熵值组成往复压缩机轴承间隙故障的特征向量。
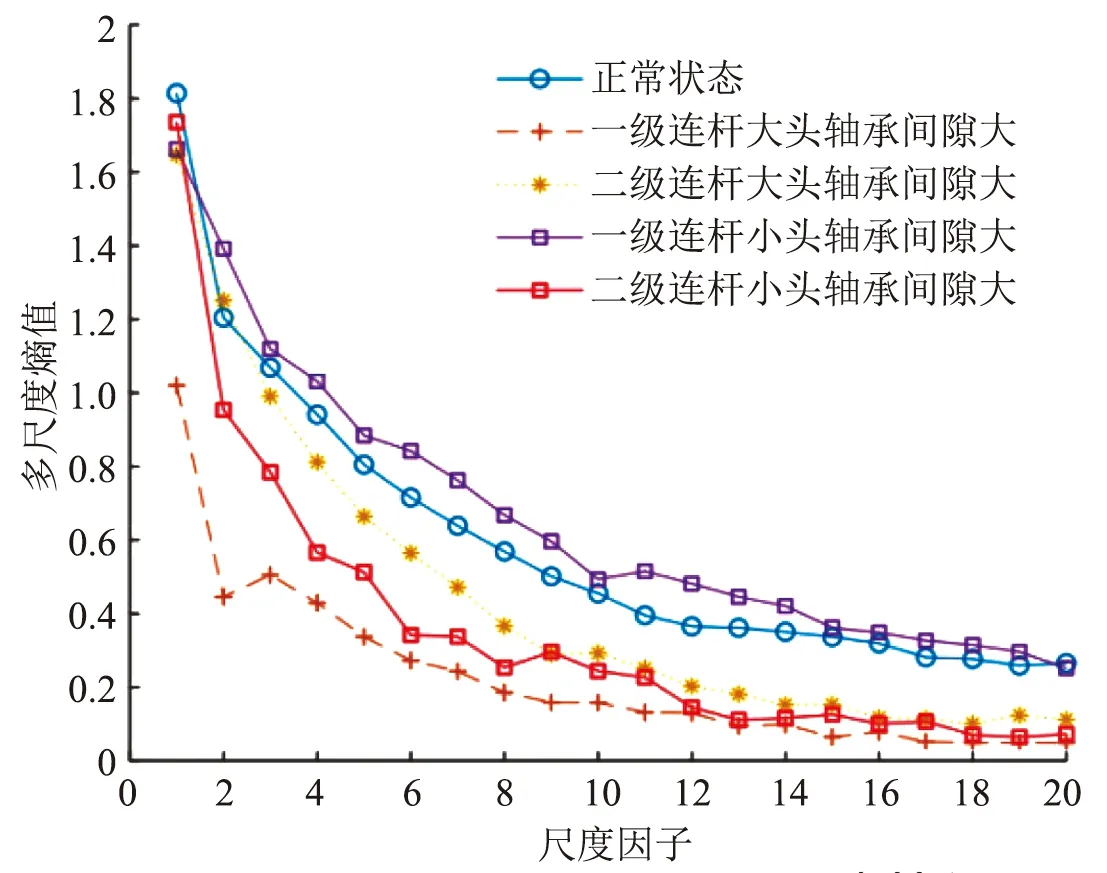
图9 不同工况振动信号的多尺度熵值图
4.2 故障识别结果对比分析
为验证本文方法应用于往复压缩机轴承间隙故障诊断的有效性与优越性,采用MCKD与MSE相结合方法,提取5种往复压缩机轴承间隙故障振动信号的特征向量,并使用极限学习机(ELM)进行特征识别[9]。
对于每种状态,选取35组振动数据,提取每组数据的特征向量,将每种状态的20组特征向量作为训练样本,剩下的样本作为测试样本,利用ELM进行故障识别,轴承状态识别模型如图10所示。
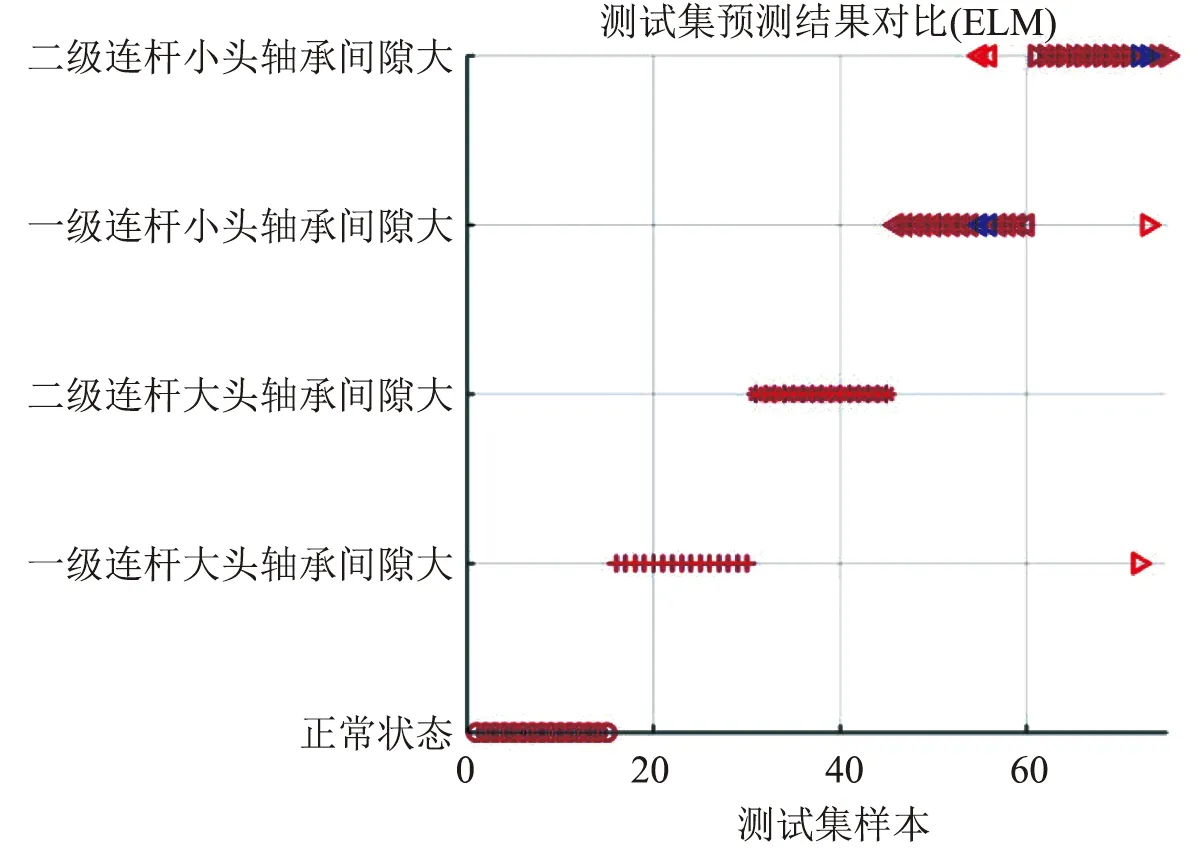
图10 极限学习机的轴承状态识别模型
采用MCKD与MSE方法对轴承故障分类识别,其准确率如表1所示。5种状态数据对比分析表明:发现本文采用的方法优于MCKD与MSE方法。
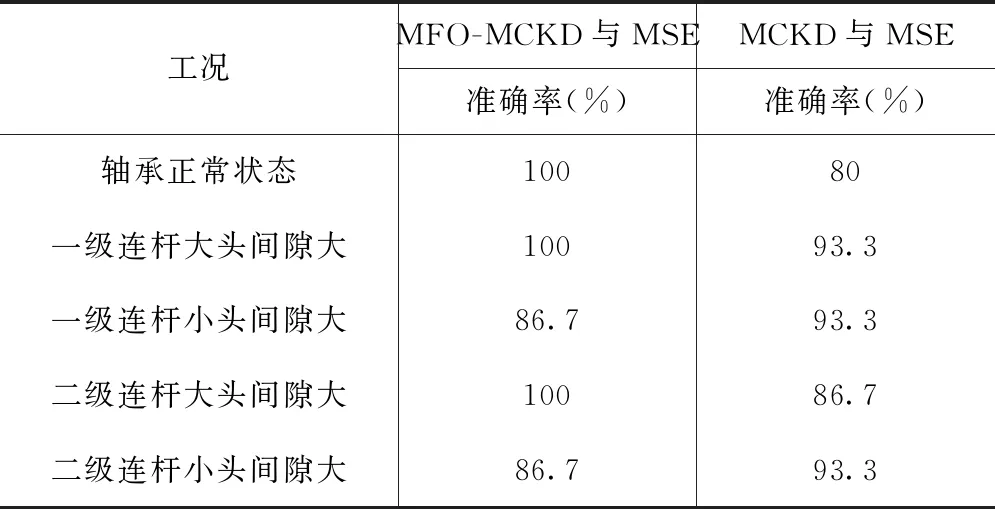
表1 2种方法的识别准确率
5 结论
本文对MCKD算法的参数进行了优化,并与MSE相结合,成功地应用于往复压缩机轴承不同状态的特征提取。通过对仿真信号和轴承间隙故障实测信号的处理与分析,得到了以下结论:
(1)利用飞蛾扑火优化算法对MCKD方法进行参数优化,避免了凭借人为经验设定参数,而影响降噪效果。通过获得最佳参数组合[L,T],以达到最佳解卷积效果。
(2)采用多尺度熵对经MCKD处理的不同状态的往复压缩机振动信号进行熵值分析,并由多尺度熵值构建特征向量。
(3)极限学习机对特征向量的识别结果表明,本文提出的往复压缩机轴承故障诊断该方法具有较高的识别率。
