基于图形仿真法的螺杆压缩机转子成形刀具廓形设计

贺诗哲，杨 剑

(1.中石化上海工程有限公司，上海 200120；2.中国船舶重工集团第七一一研究所，上海 201108)

1 引言

螺杆压缩机具有结构简单、操作方便和运转可靠等一系列独特的优点。在螺杆压缩机设计中，最重要的是设计其转子型线，转子加工精度基本决定了螺杆压缩机性能。在转子的制造加工方面，由于转子是螺旋面，成形铣刀被公认为是包络铣削螺旋曲面的高效专用刀具，在加工精度等方面具有显著地优势，在铣削效率上要比立铣刀高出3到5倍。因此，研究成形铣刀廓形对转子的生产制造具有重要的经济价值和现实意义，为此，国内外研究学者对转子刀具廓形设计方法进行了一系列深入研究。

国内在转子刀具廓形研究方面，西安交通大学朱国怀等介绍了螺杆压缩机螺旋转子啮合及加工基本原理，并以单边不对称摆线销齿圆弧转子型线为研究对象，采用包络法求解铣刀廓形方程[1]。南开大学吴大任等对涡轮蜗杆进行了透彻剖析，对圆柱蜗杆螺旋曲面的形成原理进行了必要的论述，并对圆盘铣刀和刀盘加工方法进行了全面的分析[2]。易先中等根据曲面簇的包络原理，详细分析了铣刀刀具与螺旋曲面(即工件)的相对位置和运动关系，提出了采用专用盘形刀具对圆柱螺旋齿面实现铣削加工的方法[3]。随着计算机技术的发展和应用，螺旋转子的加工技术不断得到革新。国外在转子加工研究方面，Goldfarb et al.基于齿轮传动理论知识用CAD软件开发了新的转子加工计算方法，在实际生产实际零件之前模拟齿轮的设计、制造以及检验[4]。Litvin FL根据在齿轮和刀盘之间接触点的公法线必须穿过刀盘旋转轴的概念，推导了从圆柱齿轮廓形计算刀盘廓形的数学模型，该模型亦可用于转子磨削用刀盘廓形的计算过程中[5]。Yu-Ren Wu等提出了一种在给定任意转子轮廓(转子轮廓为解析形式或离散形式)时形成用于加工转子的铣刀廓形的设计方法[6]。这些文献都是通过解析包络法获得转子的刀具廓形，但在计算复杂的刀具接触线方程时，由于导数不连续往往存在数值稳定性问题。在转子型线的导数不连续的情况下，转子刀具廓形会出现断点，还要单独把断点处的刀具廓形线补上去，容易出现干涉误差。另外在某些情况下，奇异点会出现在对应的铣刀上，这些奇异点容易在加工时产生干涉或根切的现象。因此，希望找到一种更简单、更全面的方法来代替解析齿轮包络法。

由于解析法求解螺杆压缩机刀具廓形复杂容易出现干涉，Popa Camelia Lǎcrǎmioara研究了基于包络面互补的定理，根据“替代圆族”定理，以解析法的为基础，提出了一种加工压缩机转子成形刀具廓形的方法，该方法在借助于AutoCAD对螺杆转子加工过程进行运动仿真，确定螺杆压缩机转子的成形刀具廓形[7]。Kun He a提出了一种点矢量包络(PVE)法来计算螺旋线的成形刀具廓形表面。基于该原理，螺旋表面的横向轮廓被分散成一系列点，并且通过数值方法获得离散点的法向量，然后使用PVE方法，通过刀具和螺旋面的螺旋运动形成螺杆压缩机转子成形刀具廓形[8]。虽然上诉方法避免了解析法求解的繁琐，但是由于他们是通过AutoCAD的运动仿真方法和AutoCAD的二次开发后求解刀具廓形的速度相对较慢，本文提出了一种计算螺旋曲面成形刀具轮廓的图形仿真与数值法结合的方法，这种方法速度快，精度高。基于图形仿真法求解转子刀具廓形时，将计算机图形仿真与数值方法的结合方法可以避开型线导数求解，这样就避免了刀具廓形求解出现断点，即使在双包络、干涉或根切问题时，也可以快速，精确求出转子刀具廓形，还可以用生成刀具廓形进行螺杆压缩机转子的切削过程仿真，以方便检查切削齿廓与给定齿形数据的偏差反过来验证刀具的正确性，可以减少刀具廓形的设计误差。

2 螺旋面成形铣刀廓形设计原理

2.1 螺旋面的形成

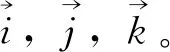
(1)

式中u——空间参数

或用直角坐标表示为

x0=x0(u)y0=y0(u)z0=z0(u)

(2)

螺旋面的方程用坐标式表示为：

x=x0(u)·cos(θ)-y0(u)·sin(θ)y=x0(u)·sin(θ)+y0(u)·cos(θ)z=z0(u)+p·θ

(3)

式中p——螺旋面导程

螺旋面如果是左旋的，把公式(3)中的θ变为负号。

在加工螺旋面的中，往往已知其端截形或轴向截形。当已知螺旋面在xoy平面上的端截形时，z=0，其截形方程式为

(4)

则由式(3)得相应的螺旋面方程式为

(5)

2.2螺旋面的法线矢量

设任意曲面的方程为

(6)

式中u、θ——曲面的2个变参数

(7)

式中nx、ny、nz——分别表示曲面上的在点M(x，y，z)的法线分量

由螺旋面刀具定义可得

nx·y-ny·x=p·nz

(8)

当已知螺旋面的端截形时，z0(u)=0和当已知螺旋面的端截形时，y0(u)=0。由式(8)得其法线矢量为

(9)

2.3接触条件及其方程式

加工具有螺旋面的工件时，螺旋面是刀具的回转面相对于工件作螺旋运动时所形成的包络面。回转面要包络出工件的螺旋面，这两个表面应沿着一条空间曲线相切接触。在刀具回转面和工件螺旋面的接触点处，有公共的法线矢量，相对运动速度应该与公法线垂直。因此，刀具与工件表面的接触线应满足基本条件式为

(10)

若已知工件的螺旋面，接触线条件式可用坐标式表示为

z·nx+C·ctg(ε)·ny+(C-x+p·ctg(ε))·nz=0

(11)

式中ε——刀具安装角

C——刀具回转面中心到螺旋面中心的距离

2.4刀具回转面轴向截形

通过坐标变换，将接触线变换到刀具坐标系(o′-X，Y，Z)中，接触线绕刀具轴线回转即得刀具回转面。则刀具回转面的轴向截形为

(12)

点集(R，Z)构成刀具回转面的轴向截形。

3 图形仿真法原理与成形刀具廓形的获取

根据需要构造转子刀具与工件实体进行交运算，其交集即为工件在该面域内的截面，因此对于仿真加工出的工件实体，其工件截面的廓形即为工件截形。依据仿真和螺旋面加工原理，本文首先提出了分层铣削运算法来获取螺旋转子齿面加工用成形刀具廓形，即采用分层铣削运算法以工件反加工用的成形刀具廓形。根据螺旋面刀具的形成特点采用UG以布尔运算完成成形刀具的轴向廓形的生成。分层铣削算法用到的是布尔运算的一种差集运算，即通过工件与刀具毛坯连续做差集运算，把刀盘毛坯加工为成形刀具。

现在以SRM-A型线的阳转子为例，基于SRM-A型线利用图形仿真算法得到了完整的一齿的螺杆压缩机成形刀具廓形，基本过程如下：

(1)工件造型；在UG环境下，在前视基准面上，插入提供的4～6螺杆阳转子工件端面截型的离散数据点，形成工件端面曲线和在工件端面形成阴阳转子外圆，形状如图1(a)～(b)，然后在圆柱任意一个端面上根据形成的圆和相关参数形成螺旋线图1(c)，最后根据螺旋面铣削轮廓和铣削路径对圆柱进行“扫描拉伸”，形成螺旋面，如图1(d)。

图1 阳转子造型

(2)刀盘毛坯造型，并摆放到合适的位置；由于螺旋面工件和刀盘毛坯中心的距离为A，并且它们的轴线夹角为∑，因此先在前视基准面上，以(0，A，0)为圆心，以刀盘毛坯半径为半径画圆，双向拉伸并绕螺旋面工件和刀盘毛坯之间的连线(Y轴)逆时针旋转∑(如果螺旋面工件螺旋线方向为右旋，则∑为正，否则为负。)结果如图2(a)所示。设计成形刀盘时，预设二个铣削安装参数——中心距A和轴线夹角为∑。图2(a)中Z轴是工件轴线，X轴是刀盘轴线，Z轴和X轴之间的最小距离即中心距A，Z轴和X轴之间的投影交角即轴线夹角为∑。然后大致设定工件实体B，刀盘柱体刀坯Bz，其厚度应比工件齿槽的法向宽度稍大，其半径比X轴到工件槽底的距离亦稍大，使B和Bz二个实体相互交迭如图2(a)。

(3)布尔运算，用工件反加工刀盘毛坯，然后获得成形刀具面；应用UG软件的运动仿真模块的实体干涉检验功能，产生螺旋面实体B和刀盘Bz之间的一系列干涉体 Bi(图2(b))。很明显，一系列Bi曲面叠加∑Bi即为属于成形刀具面。

(4)获取成形刀具轴向截形。成形刀具面形成后，然后用过刀盘轴线并与上视基准面平行的基准面与刀盘求交获得成形刀具的轴向截形如图2(c)。

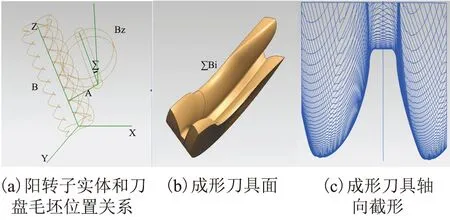
图2 形成阳转子成形刀具截形

(5)利用获取的成形刀具的轴向截型，用MATLAB提取图形提取边界的命令提取出成形刀具轴向截型的边界点的离散点数据，再对提取的边界离散点基于样条插值拟合光顺化，再以刀盘与转子的中心距为半径交螺杆压缩机成形刀具边界线就可以得到成形刀具的完整边界轮廓线的左右边界点，最后得到了完整的一齿的成形刀具廓形，如图3所示。

图3 基于计算机图形辅助设计与数值方法提取SRM-A型线的刀具轮廓线

4 成形刀具廓形设计的分析及实验验证

基于上述的螺旋面加工原理，可以得到几何仿真加工的得到转子刀具廓形，然后用得到的刀具仿真加工螺杆压缩机转子的螺旋面。在加工过程中，仿真加工出的工件螺旋面越光滑，越接近于真实加工的效果。在UG平台上利用运动仿真功能可实现这一仿真加工过程，在基于MATLAB强大的数值计算功能可得螺杆转子的成形刀具廓形。将仿真加工得到的工件实际截形与其理论截形进行对比，即可校验出所设计的刀具廓形是否正确。通过图形数值法求的无密封筋与密封槽的SRM-A型线的时的刀具反切出的SRM-A齿型线与理论法求得SRM-A型线的刀具反切的SRM-A型线在两者计算结果是一致的，如图4所示。而在求解带有密封筋和密封槽的SRM-A型线的转子刀具时，解析解求得成形刀具切削转子有过切现象。举例如下，SRM-A型线的端面数据如表1，如图5所示，可以看出用解析数学模型计算的刀具与基于图形与数值方法计算的刀具反切转子有差异，其中红线是由基于图形与数值方法计算的刀具反切加工出来的转子和蓝线是由解析法计算的的刀具反切加工出来的转子，可以

图4 解析法和基于计算机图形辅助设计与数值方法刀具反切无密封筋与密封槽的SRM-A阴阳转子

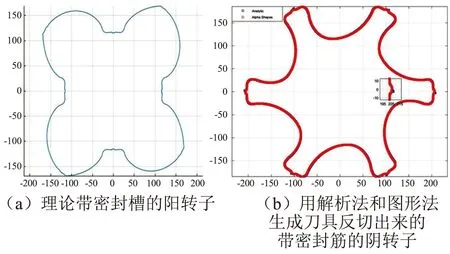
图5 解析法和基于计算机图形辅助设计与数值方法刀具反切带密封筋与密封槽的SRM-A阴阳转子

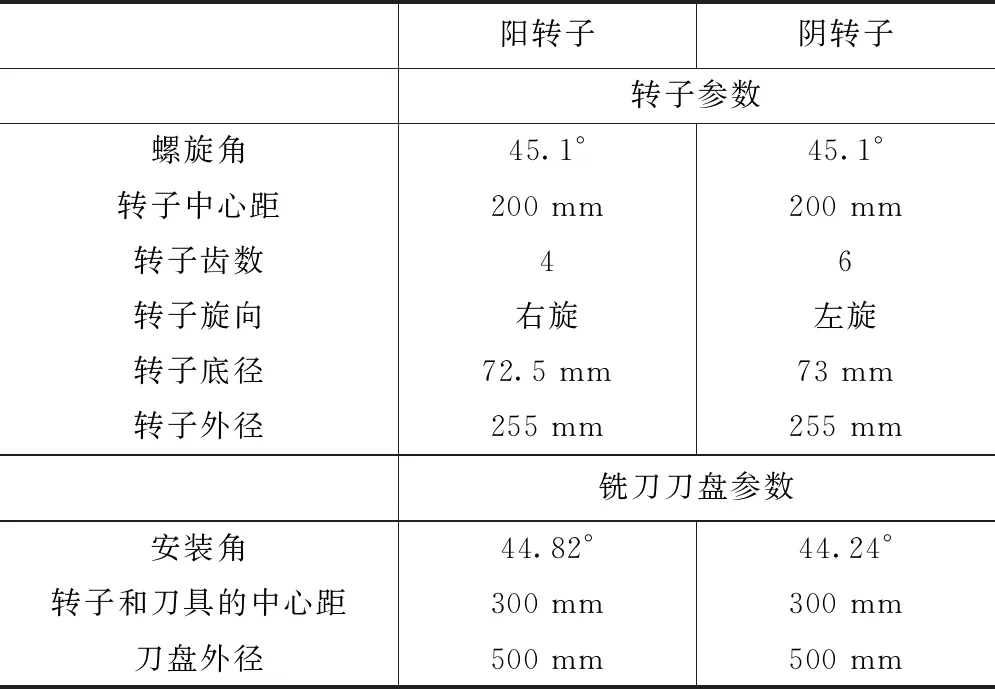
表1 SRM-A型线的刀具的设计参数

看出基于图形与数值方法计算的刀具反切加工出来的转子在密封筋的地方比较光滑，是无干涉的，而由解析法计算的刀具反切加工出来的转子在密封筋的地方是有干涉的。

为了验证本文方法的有效性，对上述方法设计的SRM-A型线的成形刀具进行了转子加工。

为了评定成形刀具切削的转子的加工精度，对转子端面进行了测量，如图6中D表示理论型线与加工出的型线法向误差，从图中可以看出阳转子法向误差最小为0.92 mm，由测量结果知，转子整体加工误差位于(-0.001 mm，+0.001 m)范围内。设计要求中转子允许的加工容差为(-0.02 mm，+0.02 mm)，可见加工出的阴、阳转子均满足该螺杆压缩机转子加工的精度要求。

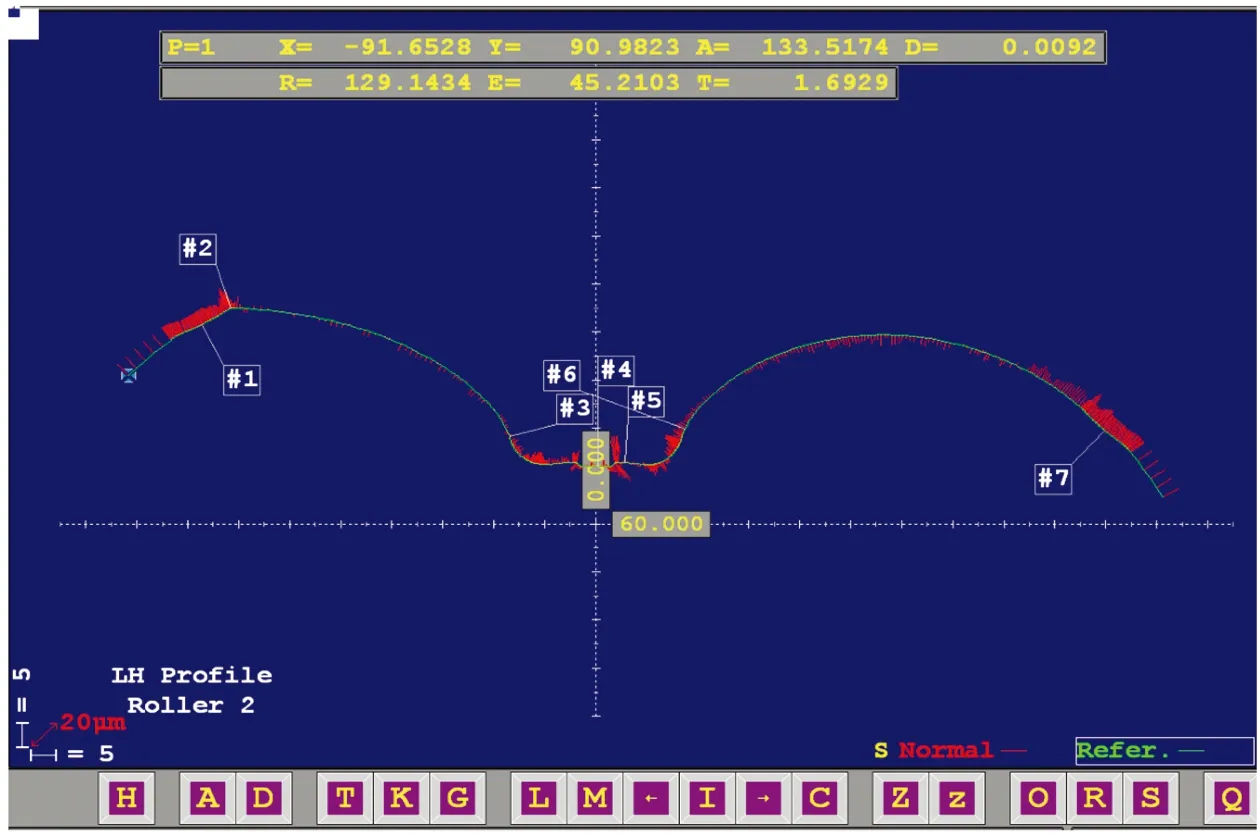
图6 SRM-A阳转子实际加工与理论阳转子的法向误差检测

5 结语

论文中提出了一种新的计算机图形仿真与数值方法加工螺杆压缩机转子成形刀具廓形的生成方法，理论分析和实验结果表明：本文的算法不仅可以省去了复杂的螺杆压缩机转子成形刀具接触线公式推导，也为复杂螺杆压缩机转子型面的刀具设计提供了新方法。这种方法比传统包络解析法更快速、直观且适应性好，主要结论如下：

(1)针对已知任意螺杆压缩机转子型线的刀具廓形设计问题，通过对转子型线坐标系的旋转变换，建立了转子坐标系与刀盘坐标系之间的几何映射关系，为任意型线转子齿面刀具廓形的计算奠定了基础。

(2)当转子型线以离散形式表达时，基于转子坐标系与刀盘坐标系之间的映射关系建立了转子与刀具的数学模型，利用图形法取代包络条件，求解得到成形刀具廓形，可以避开求转子廓形的法线，这种图形数值仿真法可以解决类似的离散点工件廓形刀具廓形的计算问题，对于解决类似的离散问题可显著提高计算精度。

(3)加工结果表明，本文提出的方法能够满足螺杆压缩机转子的加工精度要求，是一种有效的螺杆压缩机转子齿面成形刀具廓形设计方法，图形仿真法在决定刀具廓形形状或对工艺参数进行优化等方面，也有独到之处，并可推广应用于其他螺旋面成形刀盘或盘形刀具的廓形设计。