飞机降落过程数学模型研究
2022-05-18黄河基陈世杰马珺凌郭嘉俊周以明中国民航大学理学院天津300300
黄河基,陈世杰,马珺凌,郭嘉俊,周以明(中国民航大学理学院,天津 300300)
飞机最危险的十一分钟:起飞三分钟,降落八分钟,这是因为在起飞、降落过程中大多处于对流层,此处的气流变化较为显著,且高度有限,飞行员不能够很好地对飞机做出修正,一旦没有控制好力度,很容易造成飞行事故。本文通过建立飞机降落过程的物理模型、数学模型,得到两段飞机降落时的二次曲线,并利用Matlab对各个阶段的数据进行了拟合分析,从而分析各个阶段飞机的受力情况,得到所需要提供的力的大小,最后针对数值计算结果对模型进行修正、改进。
一、飞机降落过程的力学模型
飞机在降落过程中一共收到四个力的作用(如图1所示),分别为:升力、阻力、飞行员提供的推力和飞机的重力(飞机在空中的阻力一共包括摩擦阻力、压差阻力、干扰阻力、激波阻力和诱导阻力。但其中摩擦阻力、压差阻力、干扰阻力和激波阻力都与升力无关,即为废阻力,因此此处只考虑诱导阻力的影响)。

图1 飞机降落时的受力情况
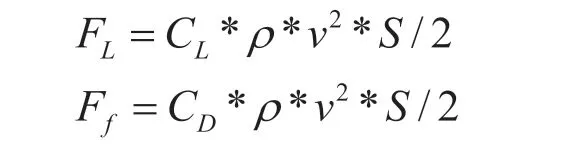

(其中FL为升力、Ff为阻力、F为飞行员提供的推力、G为飞机的重力、θ为阻力与水平方向的夹角、v为飞机的飞行速度、S为飞机的机翼面积、CL为飞机的升力系数、CD为飞机的阻力系数。)
二、飞机降落过程的数学模型
本文模型搭建是在一个二维平面中搭建的,也就是模拟飞机不受横向作用影响的理想下降过程。
根据飞机在降落过程的速度恒定不变,并且在降落的初始和末尾竖直方向上的速度均为0,因此可以考虑将它分解成两个二次曲线来进行建模[1]。
因此本文建立的数学模型将飞机的整个降落过程分为两个部分且均为二次曲线(如图2)。
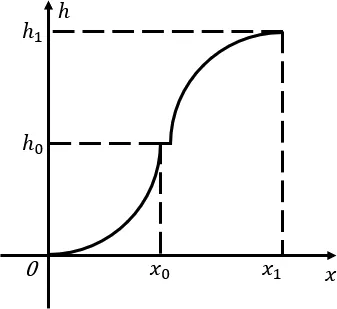
图2 飞机降落的曲线
第一阶段为从巡航高度开始降落,并且始终保持匀速,即在这个阶段始终保持受力平衡,因在下降过程中影响飞机升力和阻力的一些因素的参数大小不断变化,本文拟合变化曲线后取了最优值以将其变为一个定值以便搭建模型。
第二个阶段为进近阶段,即飞机降落的最后一个阶段,在这个阶段之前,飞行员需要预留一小段与目的地的距离,能够更好地将飞机飞行方向调整到落地方向以及跑道方向,但在进行数值计算时,由于这段距离很小,所以可以忽略不计。
第一阶段:
下落曲线为:

解得:

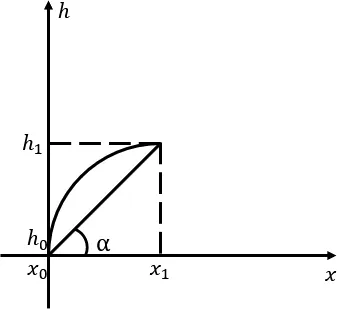
图3 飞机降落的第一阶段
第二阶段:
下落曲线为:


图4 飞机降落的第二阶段
解得:

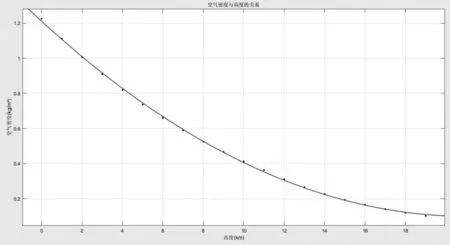
由于空气密度会随着海拔高度的不断变化而变化,因此需要确定空气密度与海拔高度之间的函数关系。

表1 空气密度ρ与海拔高度间的关系
运用Matlab将给定参数进行拟合之后得到空气密度与高度的关系式。
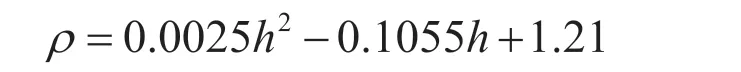
综合以上所有数据以及建立的力学模型,通过受力平衡可以预测在不同阶段的不同高度下飞行员所需要提供的水平推力大小。

(其中θ为阻力与水平方向的夹角、v为飞机的飞行速度、S为飞机的机翼面积、CD为飞机的阻力系数、h为海拔高度。)
三、数值分析与计算
波音公司的飞机作为现在比较常见的民航机型,选取此公司的机型做模型数据以用于建模和计算,现民航对于波音737的使用较多,则此处选取波音737-700机型,所以得到机翼面积为125.1(m2),巡航速度为852.9(km/h)。
在飞机降落的过程中,飞机的降落姿态呈抬头,重力的受力方向不与升力相同,存在一个抬头角度,抬头方向与其速度方向并不一致,而抬头角度的确定由具体情况而定,本文考虑飞机始终保持平飞状态,因此可以取飞机飞行的迎角始终为0,即得到升力系数:0.1,阻力系数:0.2。
目前客机正常巡航高度为11(km),进近高度为1(km)。因此设定降落第一阶段的初始高度为h1=11(km),第二阶段的初始高度为h0=1(km)。
考虑到安全因素,飞机在竖直方向的加速度a≤g/10[g为重力加速度,此处取9.8(m/s2)]。
飞机在竖直方向上的速度vy是海拔高度h关于时间t的导数,vx是水平距离x关于时间t的导数,竖直方向上的加速度是竖直方向上速度vy关于时间t的导数,因此可以得到方程组:
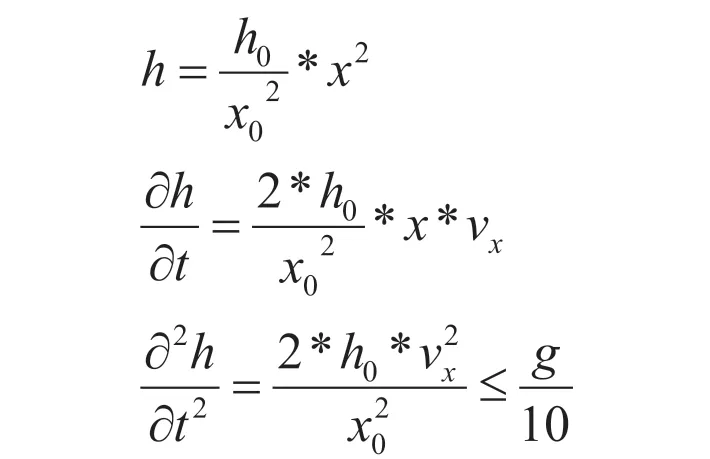
因为需要精准且安全着陆,因此我们需要得到下降点距离目的地的两个水平距离的最小值。
由上述不等式解得第二阶段降落的水平安全距离:
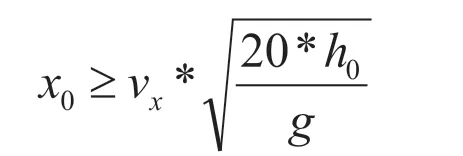
同理可得第一阶段降落的水平安全距离:
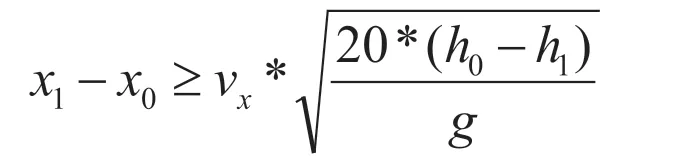
解得两个阶段下降点距离目的地的两个水平距离的最小值:

设位移偏角为α,速度的偏角为θ,由于模拟的二次曲线可以理解为平抛运动,而由平抛运动的运动规律则可得到:
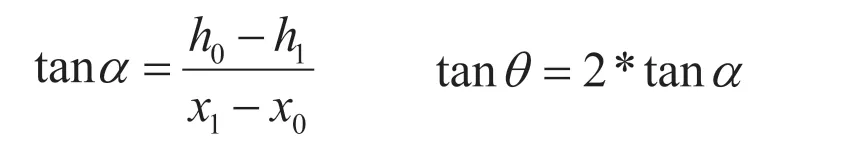
解得水平夹角θ:

代入数据之后得到F的大小,F在不同高度的大小:

(其中F1为在第一阶段的推力的大小,F2为在第二阶段的推力大小。)
四、结束语
则在飞机飞行高度h≤1(km)时,通过这个降落模型飞机可以由公式F2来参考发动机的推力大小。在飞机飞行高度h>1(km)时,飞机可由公式F1来参考发动机的推力大小。
经计算:
F1(h=11)=136532.12(N)
F1(h=1)=50420.15(N)
F2(h=1)=43614.99(N)
F2(h=0)=47368(N)
则第一阶段的发动机推力在50 420.15(N)至136 532.12(N)之间,第二阶段的发动机推力在43 614.99(N)至47368(N)之间,模型构建完毕。
