考虑地形效应的高山松地上生物量遥感估测模型构建

韩东阳，张加龙，杨 健，王书贤，冯亚飞

（1.西南林业大学 林学院，云南 昆明 650224；2.国有焦作林场，河南 焦作 454000；3.昆明市信息中心，云南 昆明 650500）

森林作为陆地生态系统的重要组成部分，是地球的碳汇主体，森林生物量直接决定了森林的固碳能力[1-2]。目前生物量的估测主要依靠样地实测数据和遥感数据的连续监测与空间分析能力，而基于遥感数据的生物量估测模型种类有很多，传统线性的参数模型预估精度较低，非参数模型精度高但因模型本身的原因可信度低以及较低的可移植性，因此没有被广泛应用[3-5]。随着遥感数据的丰富，生物量回归建模的要求和精度也随之不断提高。但生物量数据特性复杂，很难满足回归建模的正态性、同质性和残差的独立性，而只有同时满足这3 种假设，基于回归分析的结果和结论才是可靠的[6]。

混合效应模型拥有灵活的协方差结构[7]，既能体现个体间的差异又能反映样本分组间的区别。混合效应模型指模型中部分或全部参数由固定效应和随机效应两部分组成，分为线性混合效应模型（LMEMs）与非线性混合效应模型（NLMEMs），Mielke 等[8]首次提出了混合效应模型并应用。Laird 等[9]定义了混合效应模型，详细介绍了LMEMs，在纵向数据的线性回归分析引入了随机效应的概念，并且提出了最大期望算法(EM)与极大似然估计算法的参数估计法。近几年NLMEMs在国内外被很多研究人员用于林业应用研究[10-14]。在森林地上生物量估测的研究中，混合效应模型也有一定的研究应用，Huff等[15]用非线性混合效应模型量化了加州东北部常见灌木的地上生物量；Njana 等[16]利用非线性混合效应构建了坦桑尼亚最重要的3 种红树林树种的特异性和常见型地上及地下生物量模；Fu 等[17]构建了中国南方马尾松Pinus massoniana一般线性混合效应单株生物量模型，结果表明，与总体平均模型相比，混合效应模型能提供更准确的估计且具有良好的普适性；卢腾飞等[18]通过构建云杉Picea asperata和冷杉Abies fabri地上生物量混合效应估测模型并反演地上生物量；他们的研究均表明混合效应模型在森林地上生物量的估测效果要明显优于其他常见参数模型，具有较高的估测精度。

地形因子是根据林木在所处区域上坡向、坡度、海拔的不同，将坡向、坡度、海拔进行一定等级的划分。因为植被的生物量在不同坡度和坡向上具有明显差异[19-20]，而现阶段使用遥感因子和坡向、坡度、海拔等地形因子结合林木数据共同构建生物量非线性混合效应估测模型的研究较少。为了探究地形因子对生物量遥感估测的影响，本研究基于2015年与2018年的样地实测数据和同期遥感数据，构建以地形因子作为混合效应的非线性混合效应模型，并与多元线性回归和线性混合效应模型进行比较分析，同时和非参数模型的拟合估测精度进行对比。研究加入地形因子的非线性混合效应模型能否获得较高的生物量估测精度，之后选出最优的非线性混合效应模型作为生物量估测模型，为香格里拉市高山松Pinus densata乔木地上生物量获取提供更好的估测方法，并为高山地形下的林分生态效益评价提供理论支持。

1 研究区概况及数据来源

1.1 研究区概况

香格里拉市位于云南省西北部，为迪庆藏族自治州的州府所在地，地处26°52′～28°52′N，东经99°20′～100°19′E，全市国土总面积为11 613 km2，平均海拔为3 459 m，整体地形为南低北高，海拔高差较大，坡度和坡向分级明显。市内森林覆盖率高达75%，境内森林资源丰富[21]。主要优势树种为高山栎Quercus semicarpifolia、云南松Pinus yunnanensis、高山松、云杉、冷杉等。高山松为松科乔木，是我国西部高山区域的主要特有树种，高山松作为该地区的主要优势树种，占地面积1 848.18 km2，为全市国土总面积的16.18%。纯林树种主要分布在2 600～3 500 m 海拔的向阳山坡或河流两岸。高山松林在维持二氧化碳浓度和大气中碳氧平衡、碳循环以及气候变化等方面有重要作用[22]。

1.2 遥感数据

图1 研究区高山松特征与分布Fig.1 Characteristics and distribution map of Pinus densata Mast.in the research area

本研究采用USGS 下载的Landsat 8 OLI 影像数据，选取2015年与2018年无云或少云的影像共6 景，具体如表1所示。

表1 获取的研究区Landsat Level-1 影像Table 1 The collected images of Landsat Level-1 in the research area

1.3 样地调查

数据于2015年在香格里拉市实测高山松样地60 块、2018年实测高山松样地40 块[23]，每块样地面积为30 m×30 m，进行每木检尺，记录林分平均高、林分平均胸径以及分组信息，用于样地生物量的计算。

2 研究方法

2.1 Landsat 8 影像预处理

首先通过辐射校正工具将DN 值转换为辐射值，之后使用Fast Line of Sight Atmospheric Analysis of Spectral Hypercubes (FLAASH)模块进行大气校正。以校准过的SPOT-5 影像作为参照，将影像坐标系校正为北京1954，校正方法为二项式，地面控制点的选择为每景影像至少30 个，通过双线性插值将图像重新采样为30 m×30 m，并且将误差控制在1 个像素之内[24]。使用坡度匹配法进行地形校正，进行二次校正[25]后，北坡和南坡的地形阴影平均值接近，阴坡部分的反射率被阳坡部分反射率的值补偿，之后将影像拼接在一起。

2.2 因子提取

为了获取与森林地上生物量最相关的建模因子，除了单波段因子还提取了植被指数、比值因子、纹理因子、信息增强因子以及地形因子，遥感因子变量如表2所示。通过对所选遥感因子变量和AGB 的相关性分析，最终筛选出相关性最强的遥感因子为R3B1ME、R3B5DI、B547、ND64、B4Albedo。

通过外业实测小班数据的整理，按照高山松分布规律将坡度、海拔划分为5 个等级，坡向等级按照国家标准划分为9 个等级。具体分级方法以及各地形等级、样地个数如表3所示。

表2 遥感因子变量Table 2 Remote sensing factor variable

表3 坡向、坡度、海拔分级Table 3 Aspect、slope and elevation class

2.3 样地高山松生物量计算

根据研究所得高山松单木生物量公式对高山松样地地上生物量进行计算[26]，单木生物量计算公式如公式（1）所示。

式（1）中：W为单木地上生物量（kg），DBH 为胸径（cm），H为树高（m）。通过平均胸径、平均树高、株数等数据对样地生物量进行近似估算。

2.4 多元线性回归模型构建

为了区别一般线性模型与线性混合效应模型。首先构建多元线性回归模型，使用StataMP16.0 软件拟合多元线性回归模型，建模因子为遥感因子R3B1ME、R3B5DI、B547、ND64、B4Albedo 和地形因子为坡向等级、海拔等级、坡度等级。

2.5 线性混合效应模型构建

线性混合效应模型与多元线性回归相比，增加了随机效应参数，可适用于多种数据类型，且在处理非正态分布数据时更为灵活有效[27-28]。当前已有研究表明线性混合效应模型能有效提高高山松地上生物量估测精度[24]。本研究使用Matlab 2019 软件的lme 模块拟合线性混合效应模型，分别以坡向等级、坡度等级、海拔等级作为随机效应，5 个遥感因子为固定变量进行建模。

2.6 非参数模型构建

非参数模型相较于传统参数模型能够获得较高的拟合精度和预测精度[29]。为了区别非参数模型与非线性混合效应模型预估精度的不同。本研究共构建3 种非参数模型，分别为随机森林[30]（Random Forest,RF）模型、梯度提升回归树[31]（Gradient Boosted Regression Trees,GBRT）模型、K-邻近（K Nearest Neighbors,KNN）[32]模型。本研究使用机器学习工具scikit-learn 在Python3.7.4 语言环境下实现3 种算法。

2.7 非线性混合效应模型构建

2.7.1 非线性混合效应模型

构建以遥感因子为建模因子的单水平非线性混合效应模型[9]，模型的基础表达式如公式（2）所示。

式（2）中：yij和分υij别为第i个研究对象第j次重复观测的因变量和自变量值；M为研究对象的个数；为第i个研究对象重复观测次数；eij是独立分布的噪声项（随机误差项），f为预测向量与参数向量的非线性函数。φij是以非线性形式出现在函中的形式参数向量，β是固定总体参数的p向量，bi是与个体i有关的随机效应q向量，矩阵Ai与Bi分别是固定和随机效应的大小为r×p和r×q的设计矩阵，而σ2D是协方差矩阵。

2.7.2 非线性基础模型选择

构建香格里拉高山松地上生物量的非线性混合效应估测模型，首先进行基础模型的选择，选用常用的8 种非线性函数与特定的生物量模型[33]作为候选基础模型。具体模型表达式如表4所示。

2.7.3 因子拟合方式

在确定R3B1ME、R3B5DI、B547、ND64、B4Albedo 为固定变量的基础上，添加地形因子作为随机效应变量，并增加样地号和地形因子作为固定效应进行拟合对比各种基础模型下的模型精度。使用StataMP 16.0 软件nlme 模块进行拟合，分别以坡向等级、海拔等级、坡度等级为随机效应因子，样地号为固定效应因子进行初步拟合，模型形式为基础相加或相乘组合，此外还要考虑高山松本身的特征，把样地平均树高加入固定变量进行建模。为了解坡向等级、海拔等级、坡度等级为随机效应时各模型的差异，扩展出8 组基础模型，88 个具体模型。模型混合效应因子拟合方式如表5所示，表中括号内的因子表示混合效应因子。

表4 非线性基础模型†Table 4 Nonlinear basic model

表5 非线性混合效应模型因子拟合方式Table 5 Factor fitting method of nonlinear mixed-effect model

2.8 模型优度及精度评价方法

本研究模型的拟合优度指标为对数似然函数（Log Likelihood）、Akaike 信息指数（Akaike information criterion，AIC）、贝叶斯信息指数（Bayesian information criterion，BIC）3 个指标。AIC、BIC 值越小、Log Likelihood 值越大表明拟合优度越高。指标的计算公式如公式（3）～（5）所示。

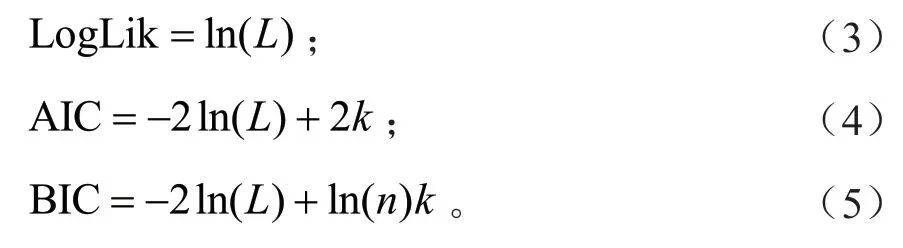
式（3）～（5）中：L为模型的似然函数，ln(L)为对数似然函数，k为模型参数个数，n为观测个数。

为了评价高山松地上生物量的预测结果，比较观测值与预测值之间的差异，需对模型进行精度检验。选取绝对平均相对误差（Absolute mean relative error,AMRE）、预估精度（Prediction precision,P）、均方根误差（Root mean square error,RMSE）作为模型的检验指标。具体计算公式如公式（6）～（8）所示。

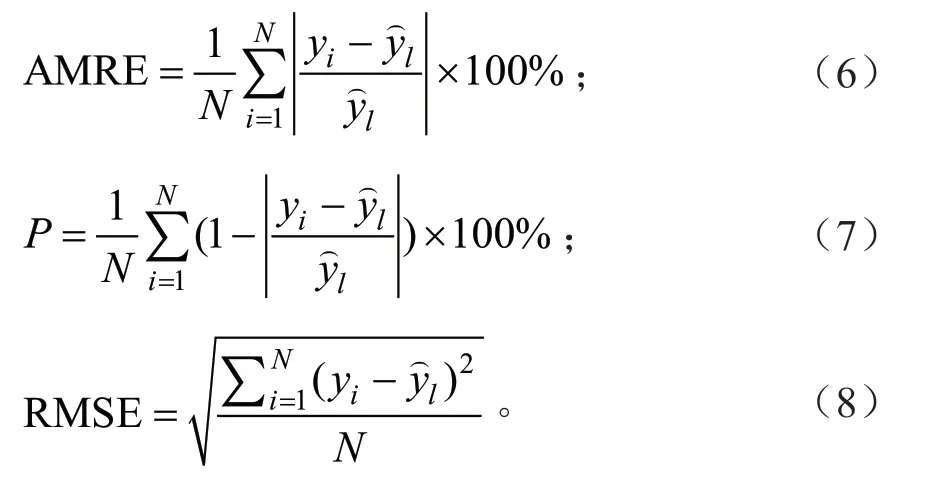
式（6）～（8）中：yi代表实测值，代表模型预测值，N为样本数。

3 结果与分析

3.1 高山松乔木地上生物量计算及统计

对2015年与2018年的共100 组样地每木检尺结果进行计算，通过使用二元材积生物量模型对样地内各样木胸径、树高进行计算后，得到100 组高山松样地地上生物量数据。其中，最小值为12.95 t/hm2，最大值为169.75 t/hm2，平均值为58.06 t/hm2，标准差为33.49 t/hm2。

遥感因子的生物量估测会在生物量的自然对数形势下表现出较强的空间自相关性。因此对所得生物量数据进行自然对数的计算。得到100 组地上生物量自然对数。其中最小值为2.56 t/hm2，最大值为5.13 t/hm2，平均值为3.90 t/hm2，标准差为0.58 t/hm2。在100 组数据中随机抽取70 组样地数据作为训练数据，剩余30 组样地数据为检验数据。样地及生物量数据如表6所示。

表6 样地和生物量数据Table 6 Plot and biomass data

3.2 多元线性回归模型构建

首先，以高山松地上生物量的自然对数值作为自变量加入5 个遥感因子，及3 个地形因子（坡向等级、坡度等级、海拔等级）构建多元线性回归模型。模型显著性为0.002 呈极显著，模型表达式如公式（9）所示。

式（9）中：LnAGB 代表高山松地上生物量自然对数。

通过计算模型的AMRE 为11.60%，RMSE 值为0.58 t/hm2。

3.3 线性混合效应模型构建

构建线性混合效应模型，自变量不变，遥感因子R3B1ME、R3B5DI、B547、ND64、B4Albedo为固定变量，分别以坡向等级、坡度等级、海拔等级作为随机效应因子，样地编号作为固定效应。模型拟合结果如表7所示。

表7 线性混合效应模型拟合结果Table 7 The fitting results of the linear mixed-effect model

结果表明样地编号为固定效应，坡度作为随机效应时LogLik 为-57.96，AIC、BIC 值为137.92、162.66。通过计算得知AMRE 为10.86%，RMSE为0.60 t·hm-2。

3.4 非参数模型构建

对100 组数据进行RF、GBRT、KNN 的拟合，训练数据和检验数据的比例为7∶3。并对建模参数及最大迭代次数进行调整，通过多次拟合后的结果得到了最佳建模参数。RF 特征参数最大迭代次数为60 次，决策树最大深度为9，叶子节点最小样本数设置为2。GBRT 最大迭代次数为20 次，决策树最大深度为9，其他参数值默认。KNN 的k值为20，权重计算方式为uniform。各模型拟合结果如表8所示。

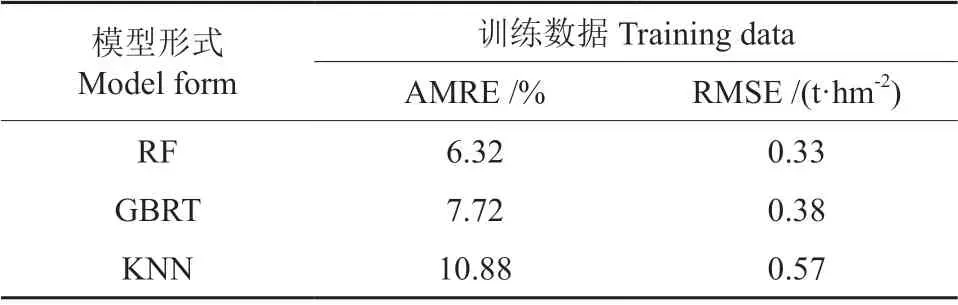
表8 各非参数模型拟合结果Table 8 Fitting results of each non-parametric model

以训练数据建模的拟合结果表明，RF 的AMRE 和RMSE 均低于GBRT 和K-NN。获 得了最优拟合效果。其中RF 的AMRE 为6.32%，RMSE 为0.33 t/hm2。

3.5 非线性混合效应模型构建与检验

3.5.1 非线性混合效应模型构建

使用70 组训练数据构建非线性混合效应模型。建模自变量为高山松地上生物量的自然对数值LnAGB。样地号、坡向等级、坡度等级、海拔等级以不同形式组合为固定效应，海拔、坡度、坡向等级分别为随机效应。通过对基础模型的构建，排除幂函数模型、对数模型、林分增长模型，得出6种可以进行拟合的模型，并对拟合结果较差的逻辑斯蒂模型和指数模型进行优化。最终共有8 种基础模型，在选择不同固定效应与随机效应因子的情况下共拟合出88 个非线性混合效应模型。其中增长模型的模型优度均高于其他7 种基础模型，共输出12 个具体增长模型。具体形式分别以坡向等级、坡度等级、海拔等级为随机效应，固定效应的组合为单样地号、样地号加一种地形因子、样地号加两种地形因子。比较12 个增长模型指标后得出以样地号、海拔等级为固定效应，坡向等级为随机效应的增长模型LogLik 值最大为-56.53，AIC 与BIC的值由于参数个数的增加略有增高分别为133.06，155.55，AMRE 为8.31%、RMSE 为0.43 t/hm2。模型优度及精度结果如表9所示。

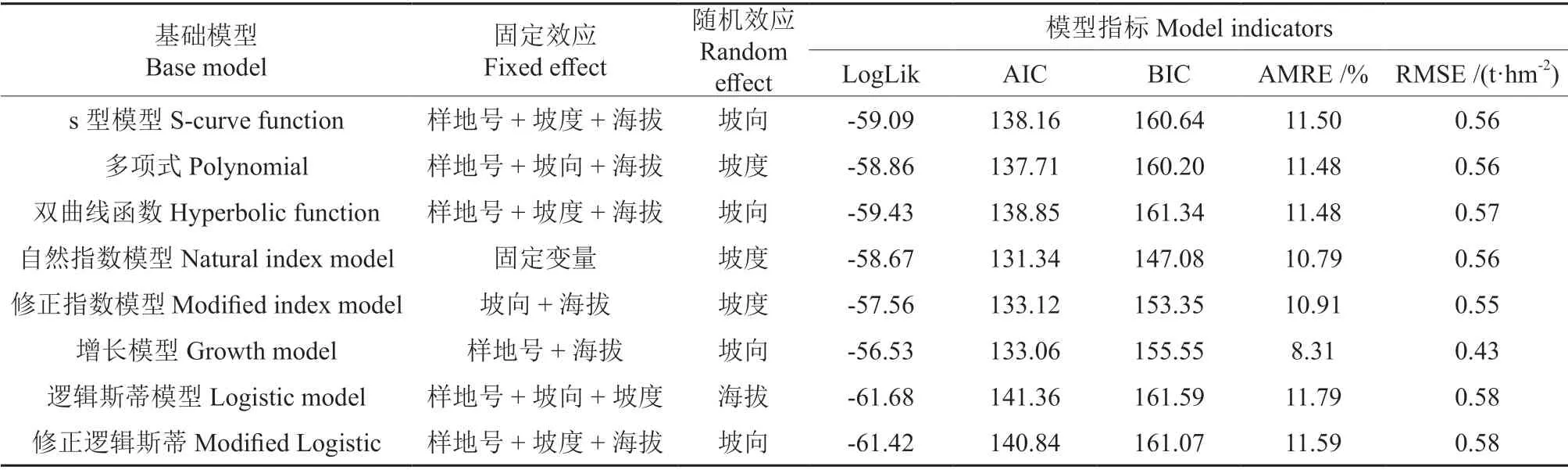
表9 不同基础模型的建模精度对比Table 9 Accuracy comparison of nonlinear mixed-effect models

3.5.2 方差-协方差结构参数确定

本次构建模型为单水平非线性混合效应模型，而模型的随机效应分别只有1 种，为单水平随机效应，因此随机效应方差-协方差结构是不相关的，方差-协方差矩阵为单位矩阵即所有随机效应都具有相同的方差[34]。故选取各模型中精度最高的模型进行方差-协方差参数的计算。通过计算得到方差-协方差矩阵为0.294 7，误差为0.004，P＞0.000 1呈极显著。

3.5.3 非线性混合效应模型检验

通过随机抽样的30 组检验数据对12 个增长模型进行验证，结果表明以坡向等级为随机效应时的预估精度最高。采用坡向等级为随机效应时，样地号作为固定效应得到预测精度P为55.33%；固定效应加入坡度等级后预估精度提高为64.80%；固定效应加入坡度等级和海拔等级后模型预估精度降低为63.14%；之后固定效应去除坡度等级，模型精度提高到84.35%。非线性混合效应模型的具体预估精度变化如图2所示。

3.5.4 非线性混合效应模型结果参数

最终确定非线性混合效应模型的基本组成形式，基础模型为增长模型，固定效应为样地号、海拔等级。固定变量为R3B1ME、R3B5DI、B547、ND64、B4Albedo，随机效应为坡向等级。模型拟合各参数结果如表10所示。

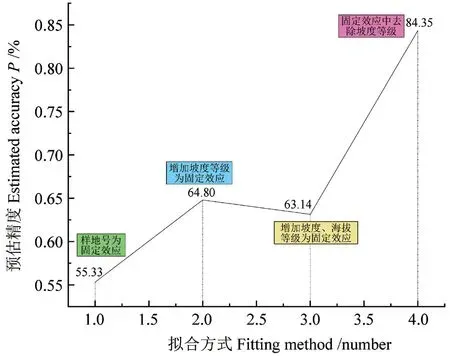
图2 非线性混合效应模型预估精度变化Fig.2 The prediction accuracy changes of nonlinear mixed-effect model

表10 高山松地上生物量非线性混合效应模型参数Table 10 Parameters of nonlinear mixed-effect model of AGB of Pinus densata Mast.

3.6 不同模型检验精度对比

利用随机抽样的30 组样地数据作为检验数据对6 种模型预测精度进行对比，并将所得估测值换算为AGB。首先是参数模型，通过比较可以看出NLMEms 的RMSE 为13.94 t/hm2，AMRE 值为15.64%，明显低于多元线性回归模型和线性混合效应模型。然后与非参数模型进行对比，非线性混合效应模型的RMSE 和AMRE 均低于3 种非参数模型。NLMEMs 的预估精度达到了84.35%显著高于其他5 种模型。各模型检验指标如表11所示。

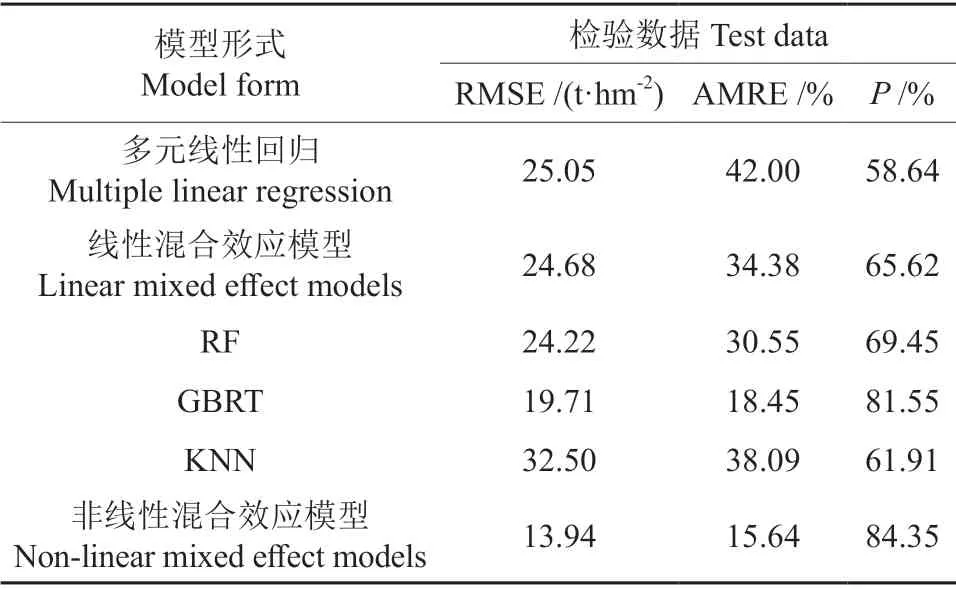
表11 模型检验精度对比Table 11 Validation accuracy comparison of models

4 结论与讨论

4.1 结 论

本研究以香格里拉市高山松为研究对象，基于8 种非线性基础模型、遥感变量、地形变量，构建了非线性混合效应模型。

1）基于遥感因子与地形因子的香格里拉市高山松地上生物量非线性混合效应估测模型随着建模因子的增加，在LogLik 值不变的情况下，AIC、BIC 的值不降反增。选择各基础模型下指标最优的模型进行比较，得出拟合优度与精度最佳的模型均为增长模型。

2）在确定最优模型的基础上，在固定效应中增加或减少地形因子，模型的预估精度最低为55.33%，最高为84.35%，而同时加入多种地形因子并不能提高预估精度。故将样地号和海拔等级作为固定效应，坡向等级作为随机效应可明显提高模型的估测精度

3）经模型精度检验后，比较3 种模型得出非线性混合效应模型的预估精度较多元线性回归、线性混合效应模型分别增加了25.71%、18.73%左右。并且预估精度高于非参数模型。

研究结果表明地形因子对生物量的估测具有一定影响，其中海拔等级和坡向等级显著地提高了模型的预估精度，为引入地形效应的遥感生物量估测研究提供了理论支持。

4.2 讨 论

本文研究了基于遥感因子的高山松地上生物量非线性混合效应估测模型的构建，在其他学者的研究中，利用植被指数和波段比值构建的高山松生物量估测混合效应模型的AMRE 为31.52%，生物量估测精度为77.83%[35]。而此次研究将地形因子和样地编号作为混合效应，对模型的非线性形式选择和优化后选出最佳模型的AMRE 为15.64%，预估精度达到了84.35%，明显提高了生物量的预估精度。当海拔等级为固定效应，坡向等级为随机效应时，生物量估测精度较样地号为固定效应时有显著提高，现阶段已有研究表明在不同海拔梯度下生物量具有不同的分配模式[36]，而海拔等级对生物量估测精度的影响，来源于不同海拔梯度下气候和物种丰富度的差异。在后续研究中，应对各地形因子进行更细致的划分。虽然模型的各项指标均高于多元线性回归、线性混合效应模型，且预估精度高于RF、GBRT、K-NN3种非参数模型。但模型的预测精度并未达到预期效果，研究可能存在以下不足：

1）目前国内外学者构建森林生物量的非线性混合效应估测模型，大多是以样地实测的单木数据以及考虑到环境因素的立地因子等数据与遥感数据相结合进行建模[17,37]。本研究仅采用遥感因子与地形因子进行模型构建，建模条件单一，未加入其他不确定性因素作为建模因子。因此在后续研究中应加入气候[38]、温度等环境因子与单木数据以继续提高模型的预估精度。

2）通常非线性混合效应模型被广泛应用于重复观测对象或重复测量数据，本次建模采用了单期样地数据，未对样地高山松地上生物量进行重复测量，因此模型预估精度较传统模型虽有提高，但效果并不理想。可考虑在后续研究中采用时间序列数据，结合森林资源连续清查数据构建动态非线性混合效应估测模型的预测效果可能优于静态模型。

3）本次研究观测样本仍然较少，随机效应的参数较为简单，主要为单随机效应参数，因此组内与组间的方差-协方差参数为定值，未充分体现个体间随地形因子对整个模型预测的影响，后续研究应增加随机效应参数，选择合适的方差-协方差结构以获取更高的高山松地上生物量非线性混合效应模型的预测精度。