背包式激光雷达林木点云帧间匹配算法比较研究
2022-05-18高世强狄海廷邢艳秋蔡龙涛
高世强,狄海廷,邢艳秋,蔡龙涛
(东北林业大学 森林作业与环境研究中心,黑龙江 哈尔滨 150040)
森林作为陆地生态系统主体,其林分碳储量是研究全球气候变化和碳循环的重要内容。而在森林资源调查中,精准地提取森林结构参数为估测森林碳储量是提供了基础的数据支持[1]。近年来,激光扫描技术以其快速、高效和高精度等特点被广泛应用于提取森林结构参数。其中,背包式激光雷达(Backpack laser scanning,BLS)免除了地基激光雷达[2](Terrestrial laser scanning,TLS)在扫描数据时的多站拼接工作,以出色的可通过性和更高的测量效率,逐渐成为林木测量的新选择[3-4]。背包式激光雷达是以3D 激光SLAM(Simultaneous localization and mapping)技术为核心[5-6],而帧间匹配是激光SLAM 系统的重要组成部分,直接影响背包式激光雷达扫描的点云精度。
目前国内外学者对帧间匹配算法进行了大量研究,其中以Besl 等[7]提出的迭代最近点算法(Iterative closest point,ICP)最为常用,该算法匹配精度较高,运行速度较快,被广泛应用于激光SLAM,但ICP 算法对初始解要求过高,在情况复杂的环境,容易影响匹配精度。为了在激光SLAM 中更好地应用ICP 算法,通常会采用特征匹配算法[8](Feature-based Method)来提高帧间匹配的速度和精度。张吉等[9]提出的LOAM(Lidar Odometry and Mapping)算法,目前在公开数据集KITTI(Karlsruhe Institute of Technology and Toyota Techno-logical Institute)上排名第一,是以点云曲率为特征值,特征提取出角点和平面点,角点用point-to-line ICP 算法进行帧间匹配,平面点用point-to-plane ICP 算法进行帧间匹配;铁小山等[10-11]提出的LeGO-LOAM(Lightweight and Ground-Optimized Lidar Odometry and Mapping)和LIO-SAM(Lidar Inertial Odometry via Smoothing and Mapping)均采用与LOAM 类似的特征提取方法,用scan-to-model ICP 算法进行帧间匹配;Deschaud[12]提出的IMLS-SLAM 算法,是以曲率和法向量为特征值,特征提取出受运动漂移最小的点,即几何结构稳定的点,利用隐形最小二乘拟合平面,最后用scan-to-model ICP 算法进行帧间匹配。由此可见,基于点云曲率特征匹配算法经常被应用在激光SLAM 算法中。除此之外,Biber 等[13]提出的NDT(Normal distributions transform)算法也经常被使用,该算法基于正态分布变换,利用高斯牛顿法进行优化,从而得到两帧之间的刚性变换,该算法匹配精度较高,运行速度稳定,在处理复杂数据时精度优于ICP 算法。这些研究中的帧间匹配算法多数作用于室内、城市街道和坡度平缓的森林环境中,在高坡度林区应用较少,且在林下作业时主要实现实时定位功能而忽视地图构建精度[14],导致目前BLS 多用于坡度较小的林地,在林下测量时数据精度要低于TLS[15]。除此之外,林下环境相较于室内和街道更加复杂,BLS 扫描的单帧数据内含大量无序点云,影响帧间匹配精度;特别是对高坡度林分下点云进行匹配时,由于坡度实时变化,算法还会受地面点云影响,使得匹配误差加大,为BLS 采集高坡度林下数据带来了巨大挑战。针对这种情况,如何选取高精度的帧间匹配算法,实现不同坡度下的精确测量,成为提高BLS 估测森林参数精度的关键。
本研究使用ICP 算法、NDT 算法、基于点云曲率特征匹配算法、基于PFH 特征匹配算法(PFH+ICP)、基于FPFH特征匹配算法(FPFH+ICP)和基于3DSC 特征匹配算法(3DSC+ICP)6 种不同的帧间匹配方法,对背包式激光雷达在不同坡度林分下所采集的单帧数据进行帧间匹配,估测匹配结果的林木胸径并计算RMSE 值和单帧匹配误差。通过对比6 种算法在不同坡度林分下的胸径提取精度,帧间匹配时的旋转误差、平移误差、欧式适合度和运行时间,得到背包式激光雷达在不同坡度林分下作业时精度最高的帧间匹配方法。
1 材料与方法
1.1 样地数据采集
本研究选取3 处坡度不同的林场作为研究区域,坡度平缓的样地位于东北林业大学哈尔滨实验林场(126°37′E,45°53′N),海拔134~142 m,年平均降雨量570.1 mm,气候属于中温带大陆性季风气候,林区覆盖蒙古栎Quercus mongolia、落叶松Larix gmelini、桦树Birch等多种人工林。坡度起伏的样地位于赤峰市旺业甸实验林场(118°09′~118°30′E,41°35′~41°50′N),海 拔800~1 890 m,年降水量400~600 mm,气候属于中温带半干旱大陆性季风气候,林区覆盖以落叶松Larix gmelini、油松Chinese pine为主的人工林和以白桦Birch、山杨Pobulus davidiana为主的天然次生林。在东北林业大学实验林场中选取一块坡度为1°的黑皮油松人工林作为实验区域,在赤峰旺业甸实验林场选取两块坡度为13°和25°的落叶松和樟子松人工林作为实验区域,3 块样地范围均为25 m×25 m。测量人员使用胸径尺和测高仪对3块样地内的单株树木进行编号并每木检尺,通过使用全站仪获取每株树木之间的相对位置,完成单木定位。3 块样地的各项属性如表1所示。

表1 样地属性Table 1 Sample properties
1.2 激光扫描数据采集
在两块样地中,使用背包式激光雷达进行点云数据获取,实验仪器采用Velodyne VLP-16 激光雷达,仪器参数如表2所示。扫描路线选取“8”字条带式闭合环路扫描,在扫描过程中保持身体平稳,避免发生巨大抖动,确保扫描后的点云受人为因素影响最小。
由于背包式激光雷达所采集的数据是所有帧的合集,不便于观察实验结果,需要对采集的数据集进行单帧提取。使用Ubuntu 16.04 和ROS Kinetic 系统,通过在终端输入指令,将“.bag”格式的数据集转化成“.pcd”格式,获取单帧数据。为了突出不同算法的匹配精度,每间隔4 帧点云选取一帧为关键帧,连续提取5 帧关键帧作为初始点云。3 块样地的单帧点云和5 帧实验点云中单株树木的初始位姿如图1~2所示。
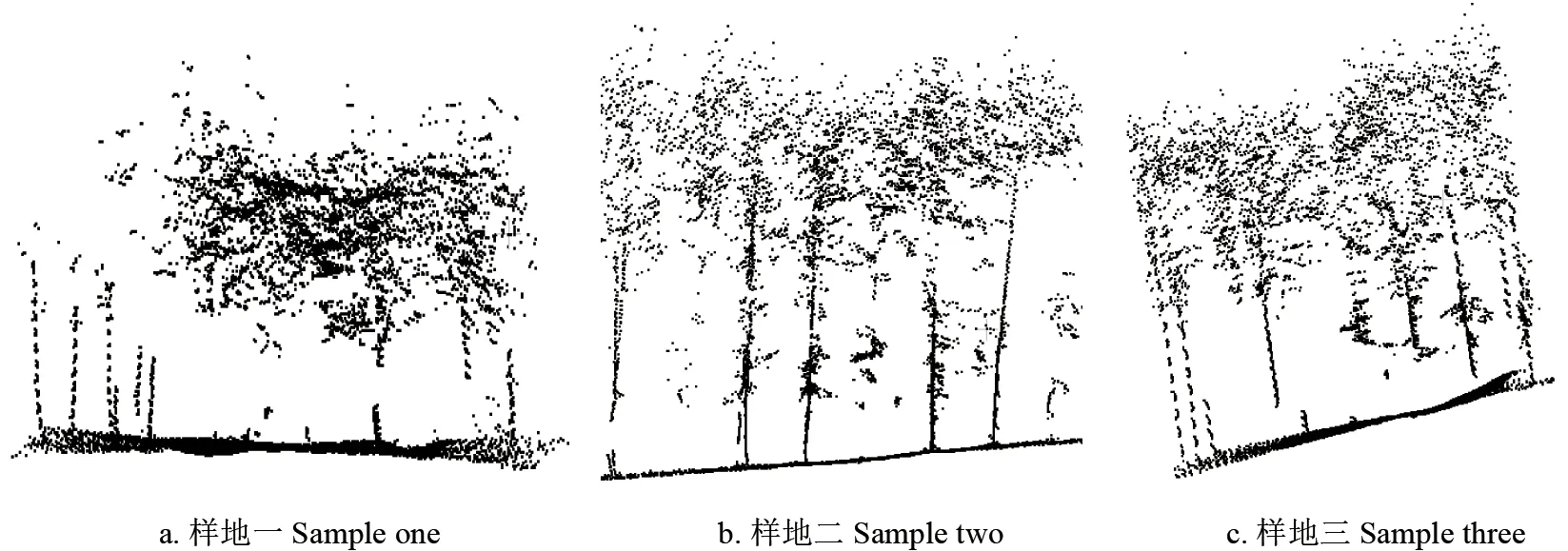
图1 3 块样地单帧点云数据图Fig.1 Sample single frame point cloud data of three sample plots

表2 激光雷达参数Table 2 Parameters of lidar
1.3 帧间匹配算法
帧间匹配算法是通过一定的旋转和平移矩阵,将不同坐标系下的两组或者多组点云数据合并到同一参考坐标系下。常见的3D 激光SLAM 帧间匹配算法大体分为:ICP 算法、NDT 算法和基于点云特征匹配算法。为了对帧间匹配算法在林下匹配精度进行全面比较,本研究选用ICP 算法、NDT 算法和基于点云曲率、点特征直方图(Point feature histograms,PFH)、快速点特征直方图(Fast point feature histograms,FPFH)和形状上下文特征(3D Shape Context,3DSC)特征匹配算法进行精度对比实验。其中,ICP 算法、NDT 算法和基于点云曲率特征匹配算法的匹配速度快、运行时间短,在激光SLAM 中应用最广;而基于PFH、FPFH 和3DSC 特征匹配算法相较于ICP 算法精度更高,对复杂环境有更好的匹配结果,且点云特征提取在PCL 库中可以快速调用,耗时较短。
1.3.1 ICP 算法和NDT 算法
ICP 算法和NDT 算法是最为常见的两种点云配准算法。ICP 算法通过欧式变换求解旋转平移矩阵,其基本原理是:在目标点云P 和原始点云Q 中,根据一定的限制条件找到最邻近点集(pi,qi),设置误差函数E(R,t),如式(1)所示。

式(1)中:n表示最邻近点对的个数;R表示为旋转矩阵;t表示为平移矩阵。通过不断迭代变换矩阵,得到最佳的R和t,使误差函数最小。
NDT 算法的基本原理:对原始点云进行栅格化,假设每个栅格内点云满足正态分布,计算每个栅格内点云的均值q和协方差矩阵C,如式(2)和式(3)所示。


通过均值和协方差矩阵构建正态分布模型p(x),如式(4)所示。
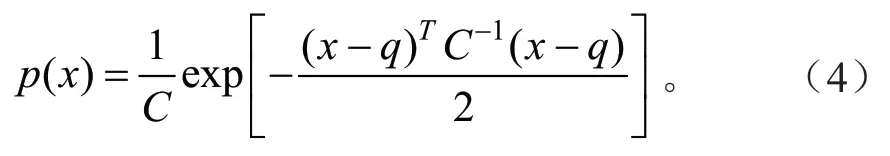
将变换过的目标点云进行变换映射到原始点云中,计算每个映射点的正态分布概率之和,将其作为评价标准score(p),如式(5)所示。

式(5)中:ix′ 表示目标点云对应原始点云xi变换后的点云坐标;qi和C表示xi对应的均值和协方差矩阵。通过高斯牛顿法进行优化,获得使score(p)最大的旋转平移矩阵。由于单帧林木点云数量较少,在使用ICP 算法和NDT 算法进行帧间匹配时,需要设置合适的下采样,保证两种算法有良好的匹配结果。
1.3.2 基于特征匹配算法
基于特征匹配算法是通过提取点云特征先进行匹配,再利用已知对应点的ICP 算法计算旋转平移矩阵,完成点云匹配过程。
1)点云曲率特征是描述点云表面凹凸情况的重要属性,通常在点云法向量的基础上进行估算,而点云法向量的计算可以简化成求协方差矩阵最小特征值对应的特征向量。协方差矩阵是由采样点的最邻近点产生的,假设点pi有k个邻近点,则协方差矩阵C的计算公式:

由于协方差矩阵C是对称半正定矩阵,所以其3 个特征值均为非负值,令λ0≤λ1≤λ2,则λ0对应的特征向量可近似采样点pi的法向量ni。点云表面曲率σ 可以通过协方差矩阵的特征值计算得到,计算公式:

为了保证基于点云曲率特征匹配算法的精度,在进行单帧林下点云曲率特征提取时,选取曲率值较大和较小的采样点作为特征点,用于帧间匹配过程。
2)点特征直方图[16](PFH)是一种常见的三维点云特征描述子,该特征是将采样点与其邻近点之间的空间信息进行参数化,形成一个多维直方图来描述点的几何特征,直方图特征具有平移旋转不变性,在复杂的环境中仍有很高的准度,可以用于提取单帧林木点云特征。PFH 是基于点与其邻近点之间的位置关系,即两者估计法线之间的空间关系,来进行点的特征描述。PFH 的计算原理如图3所示,图中表示为一个采样点Pq的PFH 的影响区域,以Pq为圆心,r为半径,将与Pq邻近的所有k点(即与点Pq的距离小于半径r的点)全部连接在一个网络中,通过计算领域内所有点之间的空间关系得到直方图,即PFH 特征描述子,其理论计算复杂度为O(nk2)。
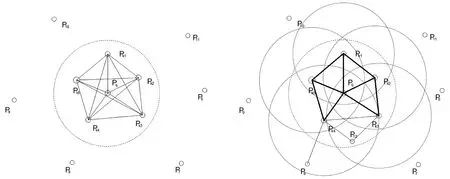
图3 PFH 和FPFH 计算原理图Fig.3 PFH and FPFH calculation scheme
由于PFH 的需要计算所有邻近点之间的相对关系,为了简化计算,提出快速点特征直方图(FPFH),该特征值只计算点与领域点之间的相对关系,计算结果称为简化的点特征直方图(SPFH),通过使用k领域内点的SPFH 计算得到FPFH,计算公式:

式(8)中:wk表示权重,通常为两点之间的距离,在图中反映为两点之间线段的粗细程度。
3)形状上下文特征[17](2D Shape Context)是一种基于形状轮廓的特征描述方法,该特征描述子在对数极坐标系下,利用直方图描述形状特征,反映轮廓上采样点的分布情况,该方法在二维图像处理中有很高的精度。2DSC 的计算原理如图4所示,通过轮廓边界采样得到一组离散的点集,以任意一点为圆心,建立同心圆,并进行平均划分,计算各扇区内的点分布数形成统计分布直方图,完成点云特征提取。

图4 2DSC 和3DSC 计算原理图Fig.4 2DSC and 3DSC calculation scheme
3DSC 是在2DSC 基础上直接扩展出来,面对于三维点云特征描述。3DSC 是以点云中任意一点Pi为球心,R为半径,构建球区域,以Pi点的法向量作为该区域的北极方向,沿半径方向,经度和纬度方向进行区域划分,最后统计落入每个区域内的点云数量,形成统计直方图,完成3DSC特征描述子。3DSC 特征描述子结构简单,辨别力强,且对噪声不敏感,在复杂的森林环境中可以清楚地表示点云特征。相较于点云曲率特征,PFH、FPFH 和3DSC 特征计算复杂,耗费时间长,需调高下采样阈值,缩短算法在进行帧间匹配时的运行时间。
1.4 精度评价方法
为了对比6 种算法在不同坡度林分下的匹配精度,将3 块样地的18 组匹配结果与地基激光雷达获取的样地一点云数据进行匹配,得旋转平移矩阵,通过旋转平移矩阵将匹配结果变换到世界坐标系中。对转化后的点云进行地面点提取,高程归一化,在高程1.3~1.5 m 处进行点云切片,通过Landau 圆形拟合算法提取林木胸径参数。通过对比样地调查时的单木位置,得到每株树木对应的实测数据,计算6 种算法在3 块样地中均方根误差(RMSE)。
在3 块样地中各选取一帧点云作为原始点云,以RMSE 值最小算法的旋转平移矩阵为基准,将两帧目标点云变换成目标点云。以转换矩阵作为标准值,对3 块样地的原始点云和目标点云进行重新配准,计算6种算法在帧间匹配时的旋转误差、平移误差、欧式适合度和匹配时间。欧式适合度[18]是指原始点云和目标点云之间的距离和,可以用于评价算法匹配精度,欧式适合度越小,算法精度越高。通过对比6 种算法匹配结果的RMSE 值,单帧匹配误差和匹配时间,得到在不同坡度林分下精度最高的帧间匹配算法。
2 结果与分析
实验平台基于Ubuntu 16.04,ROS Kinetic 和PCL 点云库,对3 块样地的5 帧点云分别用6 种算法按照采集时间顺序进行逐帧匹配。在进行帧间匹配时,为了保证算法既有良好的匹配结果又可以快速运行,6 种算法的下采样均设为0.2 m,同时将曲率特征值提取阈值设为0.4 和0.1,以便于算法有足够的特征点进行匹配。将匹配后5 帧点云融合,得到实验结果并进行单木分割。6 种算法在3 块样地中匹配结果的单木点云切片如图5~7所示。

图5 6 种算法在样地一中匹配结果的单木切片图Fig.5 Six algorithms match results in sample one

图6 6 种算法在样地二中匹配结果的单木切片Fig.6 Six algorithms matching results in sample two

图7 6 种算法在样地三中匹配结果的单木切片Fig.7 Six algorithms matching results in sample three
通过观察3 组数据的匹配结果,发现样地一的匹配效果要明显优于样地二和样地三。在样地二和样地三中,虽然6 种算法完成了对5 帧点云的匹配目标,但相比于样地一,样地二和样地三的匹配结果均存在明显的累计误差,其中基于3DSC 特征匹配算法在样地二和样地三中的累计误差最为显著。
为了检验6 种算法的匹配精度,对3 块样地的18 组匹配结果进行林木胸径参数提取,并于实测数据进行对比,计算均方根误差(RMSE),实验结果如图8所示。
从图7中可以看出,在样地一中,FPFH+ICP算法的RMSE 值最小,为2.2 cm,而NDT 算法的RMSE 值最大,为5.21 cm,ICP 算法、基于点云曲率特征匹配算法、PFH+ICP 算法和3DSC+ICP算法 的RMSE 值分别为4.16、4.86、2.41 和2.86 cm;在样地二中,FPFH+ICP 算法的RMSE值最小,为2.81 cm,而基于点云曲率特征匹配算法的RMSE 值最大,为6.03 cm ,ICP 算法、NDT算法、PFH+ICP 算法和3DSC+ICP 算法的RMSE值分别为4.67、5.85、2.91 和3.53 cm;在样地三中,PFH+ICP 算法的RMSE 值在6 种算法中最小,为4.42 cm,而基于点云曲率特征匹配算法的RMSE 值最大,为7.48 cm ,ICP 算法、NDT 算法、FPFH+ICP 算法和3DSC+ICP 算法的RMSE 值分别为5.36、7.21、4.5 和4.99 cm。
从图8中可发现,6 种算法的RMSE 值随着坡度的增大均有所上升。在样地一和样地二之间,基于点云曲率特征匹配算法的RMSE 值上升幅度为1.17 cm,在6 种算法中精度变化最大,而PFH+ICP 算法上升幅度为0.50 cm,精度变化最小;在样地二和样地三之间,FPFH+ICP 算法的RMSE值上升幅度为1.69 cm,在6种算法中精度变化最大,而ICP 算法上升幅度为0.69 cm,精度变化最小为了进一步验证算法效果,分别以基于FPFH 特征匹配算法和基于PFH 特征匹配算法在帧间匹配时获取的旋转平移矩阵作为标准矩阵,计算6 种算法在帧间匹配时的旋转误差、平移误差、欧式适合度和匹配时间,计算结果如下表3~4所示。

图8 6 种算法匹配结果估测林木胸径精度Fig.8 Estimation of DBH RMSE by algorithm matching results of 6 algorithms
通过对比表3~4数据发现,在样地一中,FPFH+ICP 算法的旋转误差、平移误差和欧式适合度分别为0.032×10-6弧度、1.25×10-6m 和27.7 m,在6 种算法中误差最小;而NDT 算法的旋转误差、平移误差和欧式适合度分别为68.31×10-6弧度、603.33×10-6m 和27.85 m,在6 种算法中误差最大。

表3 6 种算法旋转误差和平移误差Table 3 Rotation error and translation error table of 6 algorithms
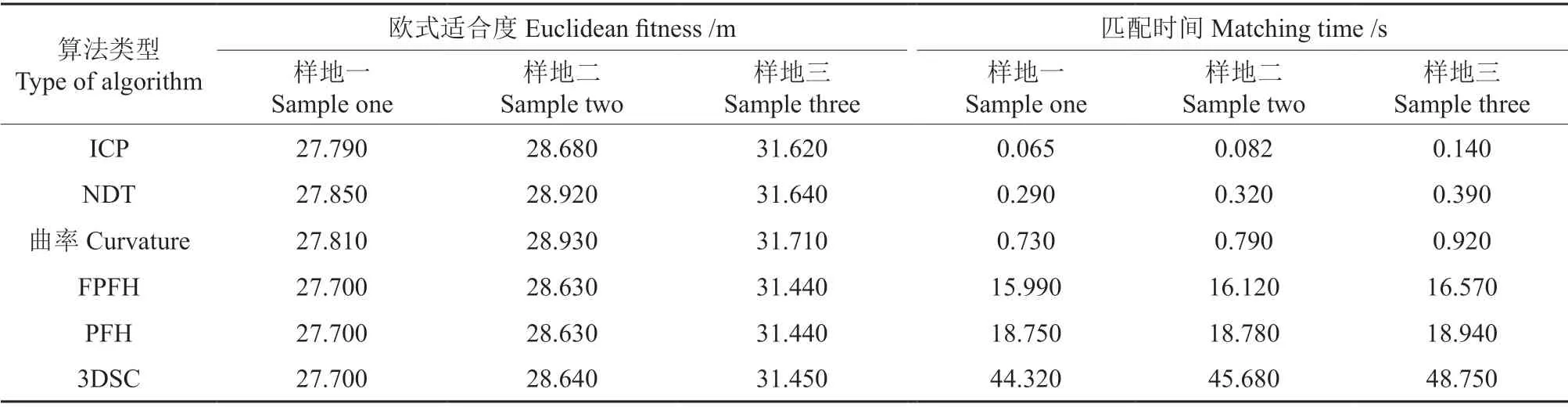
表4 6 种算法欧式适合度和匹配时间Table 4 Euclidean fitness and matching schedule of the 6 algorithms
在样地二中,FPFH+ICP 算法的旋转误差、平移误差和欧式适合度分别为0.069×10-6弧度、2.41×10-6m 和28.63 m,在6 种算法中误差最小;而基于点云曲率特征匹配算法的旋转误差、平移误差和欧式适合度分别为106.48×10-6弧度、718.36×10-6m 和28.93 m,在6 种算法中误差最大。
在样地三中,FPFH+ICP 算法的旋转误差最小,为0.18×10-6弧度,PFH+ICP 算法的平移误差最小,为5.26×10-6m,两种算法的欧式适合度相同,均为31.44 m;而基于点云曲率特征匹配算法的旋转误差、平移误差和欧式适合度分别为347.24×10-6弧度、1 406.71×10-6m 和31.71 m,在6 种算法中误差最大。其次,在3 块样地中,ICP 算法的匹配时间分别为0.065、0.082 和0.14 s,在6 种算法中均为最短,3DSC+ICP 算法的单帧运行时间分别为44.32、45.68 和48.75 s,在6 种算法中耗时最长。
3 讨论与结论
3.1 讨 论
实验结果显示,6 种算法精度均受到坡度的影响,但不同的算法受坡度的影响程度不同。通过比较6 种算法在3 块样地中的RMSE 值,对6 种算法进行依次讨论。
1)ICP 算法帧间匹配时,直接对所有下采样点云进行迭代,匹配精度受点云质量影响严重,而林下环境复杂,单帧点云质量不高,在没有良好初始值的情况下,ICP 算法容易陷入局部最优解,导致在林下匹配效果一般;但由于ICP 算法的整体匹配特性,受坡度影响小,在3 块样地中的RMSE 值变化幅度最小。
2)NDT 算法在运行时不需要寻找对应点,直接使用概率密度得分进行匹配,受坡度变化影响较小,但与ICP 算法情况相似,都需要精确的初始值来实现高精度匹配,导致在林下匹配精度不高。
3)针对基于点云曲率特征匹配算法在林下精度较低问题,在3 块样地中各选取两帧树干点云提取曲率特征值,记录曲率值最大的10 个采样点,通过对比数值,分析算法误差原因,计算结果如表5所示。观察表中数据可以看出,单帧点云内曲率特征值存在相同或相近情况,导致在确定采样点对应关系时,只依据曲率特征相似性,容易出现错误对应点对,造成算法匹配精度降低。其次,随着坡度增大,在进行点云曲率特征提取时更容易出现误差,导致算法在样地二和样地三中的匹配精度最低。
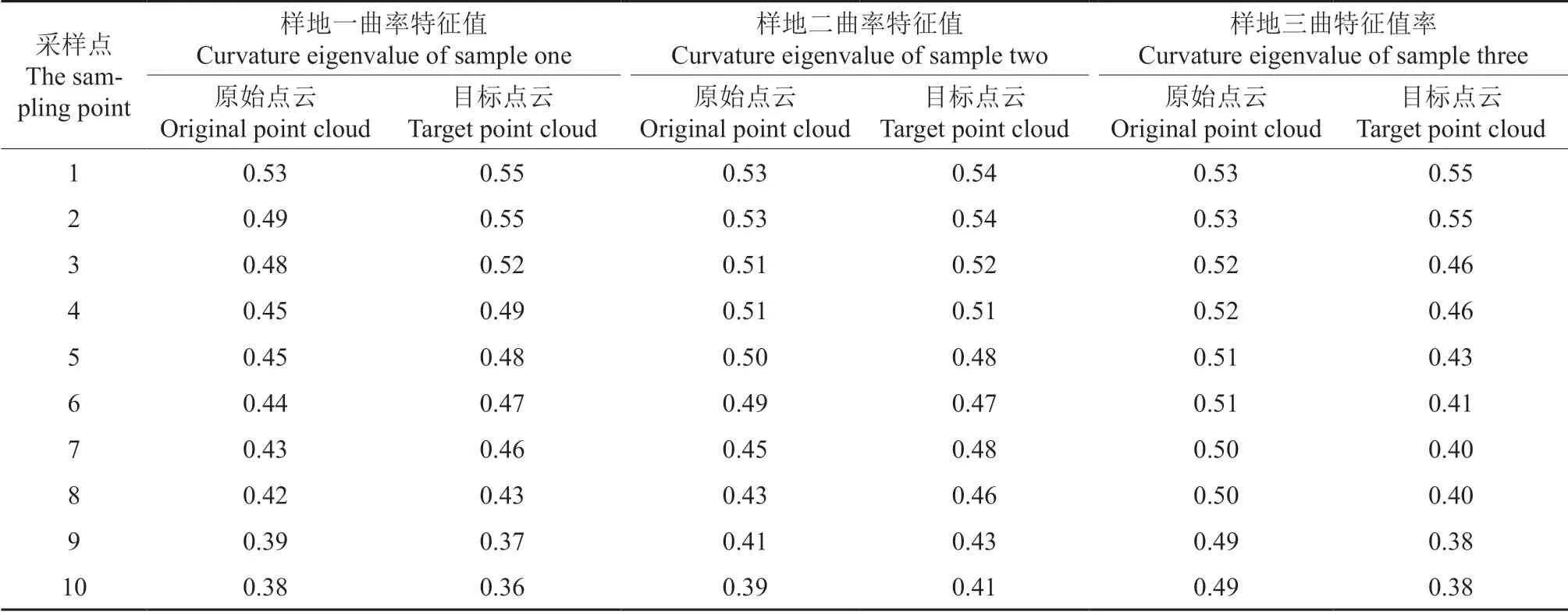
表5 3 块样地曲率特征值Table 5 Curvature eigenvalue of three sample plots
4)FPFH+ICP 算法、PFH+ICP 算法和3DSC+ICP 算法,这3 种算法的点云特征均充分运用了采样点周围点云,以FPFH 特征为例,讨论3 种点云特征在不同坡度林分下的提取精度。对3 块样地中的树干点云进行FPFH 特征可视化,可视化结果如图9~11所示。通过观察图9~11 发现,3 块样地中原始点云和目标点云的FPFH 特征基本相同,而相较于样地一和样地二,样地三中两帧点云的FPFH 特征存在明显差异。结果表明,在坡度较小的林分下,FPFH 特征清楚地反映了采样点周围邻近点分布,可以用于获取精准的对应点对,为ICP 算法提供了良好的初始值;但在高坡度林区,FPFH 特征在计算时容易遗漏重要点云,导致特征提取出现误差,使算法匹配精度降低。3DSC 特征在林下表现情况与FPFH 特征类似,但PFH 特征在计算时考虑所有邻近点参数,高坡度林区特征提取精度要优于FPFH 特征和3DSC 特征,导致PFH+ICP 算法在样地三的匹配精度最高。

图9 样地一中两帧树干点云FPFH 特征累计折线Fig.9 Accumulative line map of FPFH features of tree trunk point cloud in sample one

图10 样地二中两帧树干点云FPFH 特征累计折线Fig.10 Accumulative line map of FPFH features of tree trunk point cloud in sample two

图11 样地三中两帧树干点云FPFH 特征累计折线Fig.11 Accumulative line map of FPFH features of tree trunk point cloud in sample three
结合图8和表3数据发现,FPFH+ICP 算法、PFH+ICP 算法和3DSC+ICP 算法在样地三中的旋转和平移误差均很低,与样地二相比误差上升幅度较小,理应有同样良好的匹配结果和匹配精度,但在样地二和样地三中计算出的RMSE 值相距较大。造成这种现象是因为胸径提取精度,除了受算法匹配误差影响外,还受背包式激光雷达数据本身的影响。背包式激光雷达在扫描坡度较大的林区时,测量人员难以保持自身的平稳,在扫描过程中不可避免地发生晃动,导致采集的数据有所误差。除此之外,对比图5~7,可以清楚看出,样地一中的算法匹配结果相较于样地二和样地三树干边缘更加明显,这是因为,在扫描高坡度林地时,背包式激光雷达与林区的树木并不能保持平行关系,在扫描树干部分时出现偏差,通过圆拟合提取胸径时,造成估测结果偏大,导致数据精度较低。
本研究通过选取精度最高的帧间匹配算法来提高激光SLAM 林下建图精度,相较于乔建委[19]针对室外道路环境,利用低漂移点云和添加树木点云约束提高帧间匹配精度的方法,杨玉泽等[20]使用FPFH+NDT 算法提高了TLS 大量森林点云的配准精度和效率。本研究专注于森林环境,考虑了坡度变化对匹配精度的影响;通过估测林木胸径直接反映帧间匹配算法与森林参数的关系;在进行误差分析时,除了考虑欧式适合度外,还计算了旋转误差和平移误差,对6 种算法进行了更加精细化的比较;最后具体分析了6 种算法在林下匹配的误差原因,为多传感器数据融合,提高森林参数测量精度奠定了基础。
3.2 结 论
本研究使用了背包式激光雷达对3 块不同坡度的林地进行扫描获取单帧数据,应用6 种不同的帧间匹配算法对所选取的5 帧点云进行逐帧匹配,得到匹配结果。通过提取匹配结果的林木胸径与实测数据进行对比,计算帧间匹配误差,比较6 种算法在不同坡度林分下的匹配精度,得出以下结论:
1)6 种帧间匹配算法精度均受坡度的影响。相比于地势平缓的林地,算法在坡度较大的林地匹配精度均有所下降;其中ICP 算法受坡度影响最小。
2)6 种帧间匹配算法在不同坡度下的匹配精度高低有所不同。背包式激光雷达在测量坡度较小的林地时,FPFH+ICP 算法的匹配效果最好,精度最高;而在测量坡度较大的林地时,PFH+ICP算法的匹配精度要优于其他5 种算法。
3)背包式激光雷达在测量坡度较大的林地时,估测林木胸径精度较低,除了受帧间匹配算法误差影响外,还受数据质量本身的影响。
目前,激光SLAM 技术在各个领域发展迅猛,但在林业方面还在初始阶段。本研究虽然应用了6种不同的点云匹配方法,但还是不够全面。在未来的研究中,可以寻找更多优秀的点云匹配算法,验证其在林下环境中的匹配精度,除此之外,还可以针对林木点云特点,寻求一种最具代表性的点云特征,可以适用于各种不同的森林环境,得到一套应用于森林环境的激光SLAM 系统。
