Assessment of geodetic strain and stress variations in Nepal due to 25 April 2015 Gorkha earthquake: Insights from the GNSS data analysis and b-value

Srvnthi Gunti , Priyom Roy , J. Nrendrn , Rmesh Pudi , S. Murlikrishnn ,K. Vinod Kumr , M. Surhmnym , Y. Isrel , B. Stish Kumr

a National Remote Sensing Centre, Indian Space Research Organization (ISRO), Balanagar, Hyderabad, 500037, India

b Sustainability, Risk Management Solutions of India, Noida, 201301, India

c Department of Geophysics, Andhra University, Visakhapatnam, 530003, India

ABSTRACT A magnitude MW7.8 earthquake occurred on 25 April 2015 (referred as Gorkha earthquake). We have analyzed the spatial variation of b-value and two-dimensional strain within Nepal Himalaya before and after the Gorkha earthquake. We have used continuous Global Navigation Satellite System (GNSS) data from 30 stations in the Nepal region for geodetic strain estimation and earthquake data for b-value estimation.The GNSS data were processed using double differencing technique for the accurate position of each station.The precise velocity vectors show a general azimuth of north east for all the stations and have been used to derive two-dimensional strain. Between epicenters of Gorkha (25 April 2015) and Dolakha earthquakes (12 May 2015), we observed high co-seismic horizontal displacements (0.2 m to 2 m). In the Pre-seismic deformation study, maximum strain accumulation (56.40 × 10-9) and low bvalue (0.79-0.89) was observed in and around the Western Nepal region, which may be responsible for the 2015 Gorkha earthquake. The potential seismic zones were identified by GIS based integration of geodetic strain and b-value map and superimposition using weighted overlay method. The Maximum strain and low b-value are now observed in the eastern part of Nepal. Hence, the spatial disposition of elastic energy has changed after the two major earthquakes and continuous seismic hazard assessment is required in the eastern Nepal.© 2022 Editorial office of Geodesy and Geodynamics. Publishing services by Elsevier B.V. on behalf of KeAi Communications Co. Ltd. This is an open access article under the CC BY-NC-ND license (http://creativecommons.org/licenses/by-nc-nd/4.0/).

Keywords:Himalaya Co-seismic offsets Bernese 5.2 UNAVCO Grid_Strain

1. Introduction

Himalayas were formed by the collision of the northward moving Indian Plate with the Eurasian Plate more than 60 million years ago[1]. The orogenic process is continuous from the time of collision of the Indian Plate to present day. The region has experienced multiple earthquakes of different magnitudes [2].Earthquakes occur when the accumulation of strain in the interseismic period can no longer be countered by friction on the fault[1,3]. In the central Himalaya where moderate earthquakes occur frequently, strain may be stored in the interseismic decoupling zone to trigger great earthquakes[4,5].Based on the slip rates that derived from GPS, Jouanne [6] expected an earthquake of magnitude M ＞8 could occur in western Nepal. A magnitude M7.8 earthquake occurred on 25 April 2015, which is the first major earthquake in the Nepal Himalaya after the 1934 Nepal-Bihar earthquake (M= 8.1) [7]. The source characteristics of Gorkha earthquake show that the maximum slip of 5 to 6 m was concentrated at a depth of 8 to 15 km, 70 km southeast of the epicenter[8-10]. The earthquake was followed by a large number of aftershocks, largest of which was on 12 May 2015 (termed as Dolakha earthquake, magnitude M= 7.3) (Fig.1). Bilham [11] stated that the accumulated stress was not entirely released in the Gorkha earthquake;this unreleased energy sits uncomfortably close to the southern suburbs of Kathmandu. Sharma [12] observed in significant tectonic movement across Himalayan frontal thrust(HFT)and may trigger an earthquake in future. Hence, it is necessary to understand the spatial disposition of elastic energy in this region[13].

Fig.1. Spatial distribution of the GNSS stations.Stars indicate 25 April Gorkha earthquake(MW=7.8)and its largest aftershock(MW=7.3)with four main Himalayan fault systems overlain on digital elevation model(HFT:Himalayan Frontal Thrust,MBT:Main Boundary Thrust,MCT:Main Central Thrust and STD:South Tibetan Detachment).In the inset study area with plate boundaries (red lines) has shown with rectangular box.

Continuous monitoring of crustal deformation in this seismically active region is imperative. For understanding the relative motion between tectonic plates, techniques like satellite laser ranging (SLR), global navigation satellite system (GNSS), very long baseline interferometry (VLBI), Doppler Orbitography and Radio Positioning Integrated by Satellite (DORIS), etc. have been used[14,15].The GNSS technique has emerged as a fundamental tool for plate tectonic study with an accuracy of up to millimeter level[15-21].Geodetically derived crustal velocity field can be used for preliminary estimation of the strain-rate tensor[1,21-31].

The strain is a dimensionless quantity and is directly proportional to the stress applied to it for an elastic body [32]. There are different methods (e.g., triangular method, least square method,spherical harmonics method, multi-surface function method, etc.)to model the strain rates using GNSS velocity fields[33,34].Among these methods,the grid-based least square method is best in terms of robustness, edge effect, error distribution and method stability[34]. Teza [35] has developed a Matlab© based software (Grid-Strain) using modified least square (MLS) approach for strain rate estimation and used the same for preliminary strain analysis over the Central Apennines, Italy from GPS velocities. Kahle [26] has determined the strain rates using GPS data for the eastern Mediterranean and Asia Minor and found the largest strain rate(170 n/yr) at the North Anatolian fault zone and Kephaloniafault zone(150n/yr). Similarly, the estimation of strain using GPS measurements was carried out in the Kumaun-Garhwal Himalaya and the Kachchh region [21,23,36].

The parameter called “b-value”that depends on regional stress and tectonics is an important parameter in earthquake precursor study[37-41].The b-values characterize the stress level in different seismo-tectonic environment [42]. Difference in b-value is inversely related to changes in the stress level [43]. It can be calculated using Gutenberg-Richter (G-R) relation of earthquakes[44]. Ray [38] observed the b-value to be 0.75 for Sylhet seismic region of Dauki fault.

Number of researchers have studied the source characteristics and pre seismic deformation of Gorkha earthquake 2015 [9,28]. In this work, we add to this knowledge base, additional information regarding the state of strain prevalent during the Gorkha earthquake 2015.We have done the systematic analysis of pre and post seismic deformation of Gorkha earthquake 2015 by using 30 continuously operating reference stations (CORS) GNSS data. The GNSS data was processed using long-baseline post-processing software Bernese 5.2. The co-seismic offsets associated with the Gorkha earthquake have been analyzed using the GNSS stations in the vicinity of the two earthquake epicenters (Gorkha and Dolakha). The strain rate has been calculated with the help of the Grid Strain MATLAB™toolbox [35] using the pre and post seismic velocity fields as input. Also, we studied the b-value for before and after the Gorkha earthquake using G-R relation of earthquakes[44].We have integrated this information using weighted overlay analysis to illustrate the earthquake vulnerability in the region. The combined tool of strain estimation and b-value may provide insights into the elastic strain energy balance on the main Himalayan thrust (MHT).

2. Study area

Nepal lies along the active collision belt of the Indian and Eurasian plates. The convergence rate between India and South Tibet is about 17.8 ± 0.5 mm/yr in central and eastern Nepal,whereas in western Nepal it is about 20.5±1 mm/yr[28,45].Nepal region has experienced several moderate to major earthquakes i.e.,Kathmandu earthquake 1255 (M = 7.8), Bagmati zone earthquake 1408 (M = 8.2), Lo Mustang earthquake 1505 (M = 8.7), Northern Kosi zone earthquake 1681 (M = 8.0), Northern Bagmati zone earthquake 1767 (M = 7.9), Kathmandu/Bihar earthquake 1833(M = 8.0), Nepal/Tibet earthquake 1916 (M = 7.7), Darchula earthquake 1916 (M = 7.0), Nepal-Bihar earthquake 1934(M= 8.1), Kathmandu/Bihar earthquake 1988 (M = 6.6) and Gorkha and Dolakha earthquakes 2015 (M= 7.8＆ 7.3) [46-48].1934 (M= 8.1) and 2015 (M= 7.8) are the most destructive earthquakes in terms of human casualties(more than 8500 deaths)[49]. Based on tectonics and geology, this region has been divided into five tectonic zones from south to north i.e., Gangetic plains/Terai zone, Siwaliks/Sub-Himalaya, Lesser Himalaya, Greater/Higher Himalaya and Tethys Himalaya. The Gangetic Plains/Terai Zone is composed of alluvial sediments with nearly 1500 m thick,and is bounded by HFT in the north.The Siwaliks/Sub Himalaya are separated from HFT in the south and main boundary thrust (MBT)in the north and it consists of fluvial deposits and rich with fossils.The Lesser Himalaya is mainly composed of granitic intrusions,unfossiliferous sedimentary and metasedimentary rocks such as shale,slate,schist,phyllite,quartzite,limestone and dolomite[50].This is separated by MBT in the south and main central thrust(MCT) in the north. The Higher/Greater Himalaya is composed of mainly, granites and metamorphosed rocks such as kyanitesillimanite mineral bearing gneiss, schist and marbles. This region is separated by MCT in the south and South Tibetan Detachment System (STD) in the north. The Tethys Himalaya is mainly composed of fossiliferous sedimentary rocks such as shale, sandstone and limestone [50-52]. The Indian Plate under thrusts the Eurasian plate along a northerly dipping detachment surface,named Main Himalayan Thrust (MHT) [53,54] with ～3.5 cm/year[5,55]. The MHT with its imbricated thrust stack including STD,MCT,MBT,and HFT defines the overall structural architecture of the Himalayan fold-and-thrust belt [56]. The locking width of MHT in the western, central and eastern Nepal was 97 km, 106 km, and 129 km respectively[56,57].

3. Materials and methods

Data from an extensive continuous GNSS network of 30 stations from Jan-2013 to Aug-2017 were taken from the University of Navigation Consortium-Plate Boundary Observatory (UNAVCOPBO) (source: ftp://data-out.unavco.org) (Table 1) for the strain computation.Geographically,these stations lie in different tectonic divisions of the Nepal Himalaya.The GNSS data from UNAVCO-PBO was widely used by several researchers for different applications like geodetic studies;atmospheric studies etc.[9,17,28,58,59].GNSS data for all the stations were decimated to 30 seconds sampling interval to ensure homogeneity.The data quality was checked using the Leica Spider QC and Translation Editing and Quality Check(TEQC)software[60].The available GNSS data were processed daily using long baseline post processing software Bernese 5.2. Along with 30 GNSS stations,the International GNSS service(IGS)stations namely, Cocos (COCO), Diego Garcia (DGAR), Hyderabad (HYDE),Bengaluru (IISC), Kitab (KIT3), Lhasa (LHAZ), Quezon City (PIMO),Bishkek (POL2), Yibal (YIBL), Gangouxiang (GUAO) and Malindi(MAL2) were used as reference stations.

The supporting files like final orbits, ionospheric maps, interchannel biases, the satellite health information, leap seconds,receiver, and antenna files, etc., were taken from the analysis Centre: Centre of Orbit Determination in Europe (CODE, source:ftp://ftp.aiub.unibe.ch).

In the Tropospheric modelling, empirical model of Global Pressure and Temperature (GPT) and “GMF (Global Mapping Function)” of Boehm [61] was used. In the Ionospheric modelling,we used the linear combination(LC)and global ionospheric model(GIM) [62] and “Modified Single Layer Model (MSLM)” mapping function [62].

Due to the tectonic plate movement, the station coordinates vary with time. The reference station coordinates will be propagated to current epoch based on the station velocities.If the station velocities are not available, NNR-NUVEL-1A [63] obeying with the IERS (International Earth Rotation and Reference Systems Service)Conventions[64]was used.The deformation of the solid earth that is produced by the sun and the moon is the prevalent non-tectonic crustal deformation[65].The effects of the solid Earth pole tide and the ocean pole tide are modeled according to the IERS Conventions 2010[64].The Oceanic loading corrections were applied according to the hydrodynamics based method,Finite Element Solution 2004 model (FES2004, source: http://www.oso.chalmers.se/～loading).The atmospheric tide deformations were corrected according to the Ray Ponte model [66]. The carrier phase ambiguities were solved using quasi-ionosphere-free (QIF) Linear Combination strategy.Hence, in the present study, correction of atmospheric artefacts using tropospheric and ionospheric models and tidal corrections are carried out to nullify the effect of minute seasonal variability on the horizontal component (if any). The double differencing technique has been adopted in the processing for better accuracy.Finally, the daily-based global solution in the International terrestrial reference Frame (ITRF) 2008 reference frame is produced in Solution Independent Exchange format (SINEX) [67]. From the SINEX solution, compiled the time series in terms of geocentric coordinates (X, Y and Z) and projected to Universal transverse mercator (UTM) Projection (Northing, Easting, and Height). The outliers have removed based on the standard deviation, wherein Easting and Northing components were used for computation of 2D strain. The height components have been excluded due to its seasonal variation[68,69].Bettinelli[68]observed that,the GPS based horizontal strain variations represent the real ground deformation and the vertical component are less reliable. Kannaujiya [70]observed an agreement between GPS based horizontal displacements and seasonal loading and an inverse relation in the case of vertical displacement and seasonal loading. Dong [69] mentioned that the GPS based vertical coordinates usually have poorer accuracy than the horizontal coordinates. They observed that annual vertical variations (＜10 mm) are most significant than horizontal(easting and northing) variation (1-3 mm). Dumka [58] reported systematic variations in the up component of the GPS residual time series. Sunil [31], observed that the vertical coordinates are less precise than horizontal coordinates and used only horizontal coordinates for strain rate computation. The horizontal component derived from GNSS is not subjected to any significant seasonal variations[31,59,68,69].The data has then been separated into pre and post-event with respect to Gorkha earthquake. The period of pre-seismic data is from 01-Jan-2013 to 31-Mar-2015 (820 days),and the period of post seismic data is from 01-Jun-2015 to 28-Aug-2017 (820 days). Pre and Post event velocities of 30 GNSS stations have computed in the UTM coordinates by the least-squares method. The velocities and its margin of error values have been calculated with a 95% confidence level.

On the other hand,for estimating the b-value,we have used an earthquake catalog record with minimum magnitude of 2.5 for the period from 1980 to 2020 from National earthquake information center(NEIC/USGS:https://earthquake.usgs.gov/earthquakes),1964 to 2016 from International seismological center (ISC: http://www.isc.ac.uk/iscbulletin/citing) and 2007 to 2020 from National Center for Seismology (NCS: https://seismo.gov.in) for the present study area.The seismicity data from these sources were presented with different magnitudes(i.e.,body wave magnitude(M),surface wave magnitude (M), local magnitude (M) and moment magnitude (M)). To maintain the Homogeneity and to overcome the saturation effect of higher magnitude events,we have converted all the magnitudes into moment magnitude (M) by using therelations proposed by Das [71] and Wason [72]. The earthquakes with local magnitude M＞3.8 have equivalent moment magnitudes (M) [73], hence we considered the same in this study. The removal of foreshocks and aftershocks(de-clustering)was done by using Gardner-Knopoff windows method[74]which was modified by Uhrhammer [75].

Table 1 GNSS stations used in this study with station description and data period.

3.1. Strain estimation

The strain rate(trace of strain tensor)before and after the Gorkha earthquake have computed using the ‘strain_zero’ program of Grid_Strain MATLAB™Toolbox[35,76].This program has been used for the meaningful representation of strain data on a well-defined point [35,76]. The horizontal (Pre and Post) velocity of each station and its corresponding error have used to estimate the strain.

A smoothing parameter or scale factor is required for the modification of the least square weighting matrix in a Modified Least Square (MLS) approach [77]. The weight function “exp (-d/d0)”is used,where‘d’is the distance between the node and the grid point and ‘d’ is the smoothing parameter [33]. Except for the weighting function, the approach is described by Livieratos [78].The displacement gradient L is computed using MLS computation on each grid node and it can be written as Equation (1).

where:

E =

Ɛ

= (∂u+ ∂u)/2 = strain tensor.

Ω =ω= (∂u-∂u)/2 = rotational part of L

uis the displacement u(u)for i = 1 (i = 2 and so on).

The strain tensor E is real and symmetric and it represents the internal deformation. The rotational part Ω is asymmetric and represents the rigid body motion. The strain tensor can be diagonalized to an invertible matrix‘V’(wherein “E=VEV”;‘E’is a diagonal matrix).The Eigenvalues eand eare the maximum and minimum principal strain respectively. After the computation of the strain tensor, the corresponding trace is available for each point [35]. The strain rate described in this work is that of maximum strain (e). The summary of the approach is depicted by the flow chart in Fig. 2.

3.2. B-value estimation

The Completeness of the earthquake catalog strongly effects the b-value estimation. Magnitude Completeness (M) is defined as the lowest magnitude at which 100% of the earthquakes in space-time are detected [79]; below this magnitude, the seismic network may not record the events since they are too small or below the magnitude of interest. We used the maximum curvature method to compute the M,considering 150 samples for each sliding window for the entire period between 1980 and 2020[80].The estimated Mc has been depicted in supplementary figures(Fig.1(a and b)).

The frequency-magnitude dstribution(FMD)of the earthquakes follows a power law,known as the Gutenberg-Richter Law[44]and given by Equation (2).

where,N is the cumulative of the total number of earthquakes with magnitude ≥M; a is a constant that may change with space and time,b is a constant that defines the seismicity level of the region.

Fig. 2. Flow chart showing the methodology for strain estimation using GNSS data and b-value estimation using earthquake catalogue.

The b-value is inversely proportional to stress accumulation and the average b-value is approximate‘1’and varies with region[81].A decrease in b-value shows stress accumulation and a chance of earthquake occurrence in and around that region in future[81,82].For estimation of the parameters in G-R relation, we have used maximum likelihood estimation(MLE)method[83]which is given by Equation (3).

where Mdenotes the average magnitude of the catalog,Mis the magnitude completeness, and △M is the binning width of the catalog.

The grid interval for estimation of b-value is 0.3×0.3with a minimum number of 50 events and M＞Min each grid[84,85]for every window, we have chosen 200 events. We have used ZMAP software for the above calculations and statistical analysis [80].

4. Results

4.1. Co-seismic positional changes

The Continuously Operating Reference Stations (CORS) GNSS data were processed using long-baseline post-processing software Bernese 5.2. The daily based continuous time series in terms of change in easting and change in northing for stations CHLM,KKN4 and SNDL which are near to the epicenter have shown in Fig.3 and for the remaining sites the same are given in the supplementary file. The co-seismic horizontal offsets have calculated using the easting and northing components for each station. The computed co-seismic offsets that associated with the Gorkha earthquake using available GNSS stations for the time period of 15-Apr-2015 to 05-May-2015 were given in Table 2.

4.2. Pre and post seismic strain analysis

Fig. 3. Continuous Time series in terms of Easting and Northing in meters for (a) CHLM station, (b) KKN4 station and (c) SNDL station; which are in immediate vicinity of the epicenter. (Star indicates the date of Gorkha earthquake 2015).

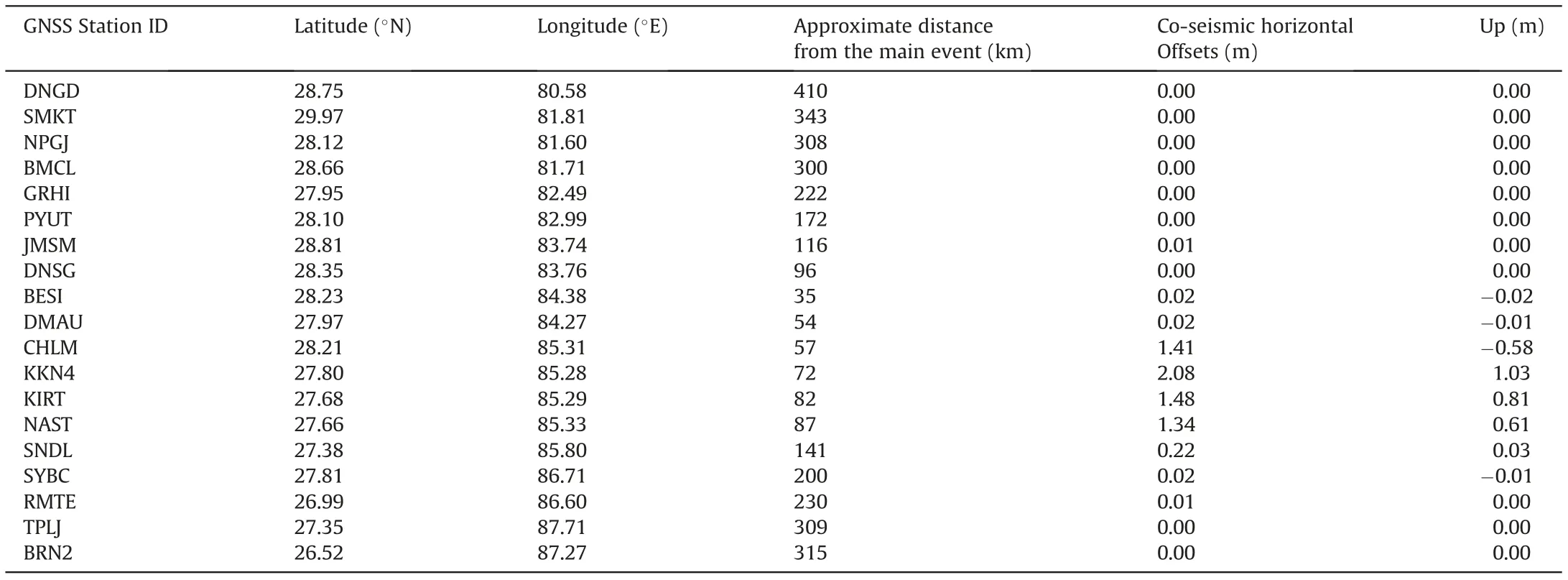
Table 2 Co-seismic offsets associated with Gorkha earthquake.

Pre-Seismic strain estimation was carried out using velocity vectors from the GNSS data for a period of 01-Jan-2013 to 31-Mar-2015 (Table 3). The estimated velocities before Gorkha earthquake ranges 40 to 53 mm/yr across all the stations with a general azimuth of north east (Fig. 4a (i)). We have benchmarked all the station velocities(DNGD,BMCL,JMLA,GRHI,JMSM,KLDN,SIM4,RMJT,RMTE and SYBC) with velocities estimated by Jade [17]. The differences between these velocities are in the order of 1-5 mm/yr thus exhibiting steady-state movement before the earthquake.

Post-seismic strain estimation was achieved using velocity vectors from the GNSS data from 01-Jun-2015 to 28-Aug-2017(Table 4).Post-earthquake velocities vary from 35 to 59 mm/yr with a general NE azimuth (Fig. 4a (ii)).

4.3. B-value analysis

The b-value of Gutenberg-Richter relation is a tectonic parameter which depends on regional stress, tectonics and period of study [81]. The average b-value is approximately ‘1’ and ranges between 0.5 and 1.5 based on the structural heterogeneity and stress distribution in the region [81,86]. The change in b-value is used as an earthquake precursor [81]. It was found that a good correlation between stress and b-value in several parts of the world[37,81].The b-value for the Central Himalaya was 1.15 representing the compressional region[42].

In this study, the b-value of G-R relation for Nepal region was estimated using MLE method.The earthquake data from 27 March 1964 to 21 April 2015,and 25 April 2015 to 24 Mar 2020 was used for b-value estimation in Pre and Post seismic deformation study respectively. The average value of magnitude completeness (M)before and after the Gorkha earthquake was 4.3 and 3.9 respectively.In the pre-seismic deformation study,the range of b-value in western, central and eastern region was 0.79-0.89, 0.8 to 0.9 and 0.78 to 0.87 respectively.In the post-seismic deformation study,the range of b-value in western, central and eastern region was 0.88-1.08, 0.77 to 1.08 and 0.71 to 0.96, respectively. The b-value for the Tibetan plateau was observed at 0.5 to 1.6 [87].

4.4. Integration of geodetic strain and b-value maps

To understand the earthquake potential zones, we have integrated the geodetic strain and b-value map using GIS-basedtechniques. For this, the geodetic strain and b-value map in raster format were reclassified into 3 classes (Table 5) based on the frequency distribution and available information in the associated domain.Then,integrated the reclassified maps using the weighted overlay method[88].This method is used to analyze the multiclass maps based on the importance of each layer. In the decisionmaking process, equal influence (50%) for the geodetic strain and b-value was used. Finally, the seismic potential map was made by grouping the raster into different zones, i.e., very low (1), low (2),medium (3), high (4), and very high (5).

Table 3 Pre-seismic velocity and strain estimates.

5. Discussion

The GNSS stations(CHLM,KKN4,KIRT,NAST and SNDL)located in and around the epicenters of the Gorkha and Dolakha earthquake (12 May 2015) shows high co-seismic horizontal displacements (0.2 m-2 m) (Fig. 5). The stations (KKN4, KIRT, NAST and SNDL) located in Kathmandu region were showing an uplift of 0.03 m-1.03 m.Similar results were reported by Yadav[9].Most of the structural damages were observed by local site effects induced by soft alluvial soil deposits,ridge effects and foreland basin effects in the Kathmandu Valley and nearby villages [89]. Taloor [90]suggested that the basins with high dissection, tilt and deep ‘V’shape valleys are more vulnerable for hazards. The stations in western and eastern Nepal which are away from the Gorkha earthquake epicenter show negligible co-seismic offsets (Fig. 5).The rupture for this earthquake remains blind,thus increasing the potential for future earthquakes [9]. The moment tensor solution from teleseismic data indicates that,Gorkha earthquake generated a cumulative seismic moment of 0.9195 × 10Nm [91].

In the Pre-seismic deformation study, it was observed that the velocities around the HFT and MBT were higher (49-53 mm/yr)than those around MCT and STD (40-49 mm/yr). The principal strain estimated from the GNSS velocities, shows that maximum strain tensor found in western Nepal was 56.40 × 10per year,whereas central and eastern Nepal were 21.30×10per year and 15.40×10per year,respectively(Fig.4b(i)).The generated strain map in accordance with the strain estimates shows significant strain accumulation in the western region of Nepal(Fig.6a(i)).Also,relatively a low b-value (0.78-0.89) was observed in the western and eastern Nepal region(Fig.6a(ii)).This indicates the high stress accumulation in these regions. The western and eastern Nepal regions has not experienced any major earthquakes after the Darchula earthquake (M = 7.0),1916 and Nepal-Bihar earthquake(M= 8.1), 1934 respectively. Hence, the significant strain accumulation and low b-value in the western region is responsible for the Gorkha earthquake [6]. Stevens and Avouac [92] observed maximum shear stress at the epicenter of the Gorkha earthquake.Tiwari and Paudyal[30]also observed a low b-value of 0.89 at the Gorkha earthquake region. Similarly, a low b-value was observed during M6.0 Parkfield,California earthquake[93].Slightly high bvalue (0.8-0.90) in central Nepal region (Fig. 6a (ii)) indicates the lesser structural heterogeneity in this region.

In the post-seismic deformation study,the GNSS stations(KKN4,LMJG,SNDL and SYBC)lying in the earthquake rupture propagation zone have shown a decrease in velocities (Fig. 4a (ii)). From the principal strain data generated using the GNSS velocities,it is seen that there is a substantial change in the spatial distribution of accumulated strain, pre and post the earthquakes (Fig. 4b (ii)).There has been significant dissipation of strain after the earthquake, especially around the western Nepal region. The estimated maximum strain tensor in the Western Nepal is 19.50 × 10per year, which is lower than that estimated before the earthquake(～56 × 10per year). In the Gorkha earthquake, the region downdip from the interseismic decoupling zone did not participate in significant strain release [94]. The central region of Nepal does not show any change in the strain with a magnitude around 21 × 10per year, whereas the eastern region shows strain accumulation with a magnitude of 174 × 10per year. The South Western region of Nepal shows a maximum strain of 61.7 × 10per year. The generated strain map(Fig. 6b (i))in accordance with the strain estimates shows the dissipation of strain in the western Nepal region and accumulation in the eastern regions,post Gorkha earthquake and the Dolakha aftershock. This may indicate a possible un-ruptured segment of the fault wherein strain accumulation is continuing and may trigger another earthquake in the future [11,95,96]. Seismological and Global Positioning System(GPS)observations have shown that the stress has been transferred to adjoining regions of the Gorkha earthquake and hence creating the possibility of future rupture on Main Himalayan Thrust (MHT)adjacent and up dip of Gorkha earthquake[9,97].Also,there was a significant change in the b-value after the Gorkha earthquake 2015(Fig. 6b (ii)). In the post-seismic deformation study, the b-value in the western Nepal was observed to be 0.88 to 1.08,which is higher than before the Gorkha earthquake. This indicates, the stress was released during the Gorkha earthquake.The b-value(0.77-1.08)in central region was increased after the Gorkha earthquake. The bvalue in the eastern region(0.71-0.96)was slightly decreased after the Gorkha earthquake which indicates the stress accumulation in this region.

Fig.4. a(i)and a(ii)Velocity vectors with error ellipses for Pre seismic deformation and Post seismic deformation respectively,b(i)and b(ii)Principal strain axes for Pre seismic deformation and Post-seismic deformation respectively (Red: Compression and Blue: Extension).

Fig. 5. Co-seismic horizontal offsets in meters associated with the Gorkha earthquake 2015 and the inset shows the variation of co-seismic offsets along the profile AB.

Table 4 Post-seismic velocity and strain estimates.

Table 5 Reclassification classes and subclass weights for each layer.

Fig. 7 shows the plot of b-value variation along profile ‘AB’ in Fig. 5. The blue and orange lines indicate the b-value variation before and after the Gorkha earthquake 2015. It was clearly observed that the b-value increased in the western and central Nepal region after the Gorkha earthquake, whereas in the eastern region,the b-value slightly decreased.

From the integration of geodetic strain and b-value map, we observed high to very high earthquake potential zones in the western and eastern Nepal regions adjacent to the two epicenters (Gorkha and Dolakha) before the Gorkha earthquake 2015(Pre-seismic deformation) (Fig. 6a (iii)). Sreejith [28] had similar observations of strain accumulation and low b-value at the epicenter of the Gorkha earthquake. Low to medium earthquake potential zones was observed in the remaining regions of Nepal before the Gorkha earthquake 2015. In the post seismic deformation study, we observed high to very high earthquake potential zone in the eastern Nepal region and low to medium earthquake potential zone in the remaining regions of Nepal(Fig. 6b (iii)). In this way, the combined analysis of b-value and strain accumulation study will be helpful in understanding the earthquake potential zones.

Fig. 6. a (i) Strain map, a (ii) b-value, a (iii) Seismic potential map for Pre-seismic deformation and b (i) Strain map, b (ii) b-value, b (iii) Seismic potential map for Post-seismic deformation.

6. Conclusions

We have carried out pre and post-earthquake two-dimensional geodetic strain and b-value analysis for the Gorkha earthquake using GNSS data and historical earthquake data. The estimated velocities before the Gorkha earthquake range from 40 to 53 mm/yr across all the stations in Nepal region with a general azimuth of North East. Further, the velocity at HFT and MBT shows a slightly higher velocity(49-53 mm/yr)than the velocity(40-49 mm/yr)at MCT and STD. In the Pre-seismic deformation study, maximum strain accumulation (56.40 × 10) and low b-value (0.79-0.89)was observed in and around the Western Nepal region,which may be responsible for the 2015 Gorkha earthquake.The maximum coseismic horizontal displacements were observed from 0.2 to 2 m for the stations,namely CHLM,KKN4,KIRT,NAST and SNDL which are lying in and around the two epicenters(Gorkha and Dolakha).The stations KKN4,KIRT,NAST and SNDL,which located in Kathmandu region, have uplifted to 0.03 m to 1.03 m during the Gorkha earthquake. GNSS stations (KKN4, LMJG, SNDL and SYBC) in the earthquake rupture propagation zone have shown a decrease in velocities after the Gorkha earthquake.The potential seismic zones were identified by GIS-based integration of geodetic strain and bvalue map and superimposition using weighted overlay method.The Maximum strain and low b-value are now observed in the eastern part of Nepal.After the(M=8.1)Nepal-Bihar earthquake(1934), there was less seismicity in the eastern region. The spatial disposition of elastic energy has changed after the two major earthquakes. Hence, based on the two dimensional strain analysis and b-value estimation,it is observed that there is a chance to occur a major earthquake in the eastern region.The combined analysis of strain accumulation and b-value are complementary techniques in seismic hazard assessment.

Conflicts of interest

The authors declare that there is no conflicts of interest.

Acknowledgements

We thank Director, NRSC and Deputy Director, Remote Sensing Applications Area, NRSC for their continuous support and encouragement. We thank UNAVCO PBO for enabling free access of GNSS data.We extend our sincere thanks to Giordano Teza and team for providing Grid Strain software.

Appendix A. Supplementary data

Supplementary data to this article can be found online at https://doi.org/10.1016/j.geog.2022.01.003.