资源可用量不确定和活动多模式情形下的随机项目调度问题
2022-05-17谢芳徐哲于静
谢 芳 徐 哲 于 静
(1.山东工商学院 金融学院 金融服务转型升级协同创新中心,山东 烟台 264005;2.北京航空航天大学 经济管理学院,北京 100191;3.天津理工大学 管理学院,天津 300384)
0 引言
资源受限项目调度问题(Resource-constrained project scheduling problem,RCPSP)是指在有限的人员、机器设备等可更新资源和活动间紧前关系的约束下,合理配置资源并确定各活动的开工时间,从而确保项目的一个或多个性能指标最优[1]。多模式资源受限项目调度问题(Multi-mode RCPSP,MRCPSP)是RCPSP的推广,项目中每个活动都可能有多种执行模式,每种模式对应一个工期和可更新资源需求量的组合[2]。经典的RCPSP和MRCPSP在建筑工程和软件开发等项目中具有很强的应用背景,其优点是能充分考虑到可更新资源可用量的限制和优化配置问题,故能在开工前为项目管理者提供进度计划作为决策依据,不足是并未考虑到实际项目调度中的各种不确定因素,如天气变化、员工劳动生产率变化引起得活动工期不确定,机器设备故障维修、员工请假休假、工作场地因突发事件停工等导致的可更新资源可用量不确定[3]。因此,如何在不确定情形下有效利用不断更新的项目数据为项目调度提供动态决策依据,对指导项目调度实践具有重要意义。
目前,不确定环境下项目调度的主要研究方法可分为两大类:随机调度和鲁棒调度[4]。随机调度是将调度问题视为多阶段的决策问题,在每个决策阶段,不断利用调度策略进行决策直至项目完工。对于活动工期不确定环境下RCPSP的随机调度,学者们提出了多种静态策略,即在项目开工前就确定而在调度过程中不发生改变的策略。基于最小禁忌集的概念,Stork[5]分别研究了最早开始策略、预选策略和线性预选策略,通过构造不同的分支定界算法对策略之间的差异进行了比较。Tsai和Gemmill[6]提出了基于资源的策略,该策略类似于并行调度生成机制,并设计了相应的禁忌搜索算法。 Ballestín[7]以及 Ballestín 和 Leus[8]分别通过遗传算法和贪婪随机自适应搜索过程研究最优活动列表策略。Ashtiani等[9]提出的预处理策略类似于最早开始策略和基于资源的策略的结合,由活动对集合和活动列表构成,通过活动对集合添加一些额外的完成-开始型紧前关系约束以解决资源冲突。Rostami等[10]对预处理策略进行了推广,除了添加完成-开始型约束,还包括开始-开始型约束。与以上静态策略不同的是,Li和Womer[11]研究的是动态策略,该策略在项目执行过程中依据实际进展情况作出决策,设计了Rollout算法在各决策阶段处不断调用基于约束规划的启发式算法对各个可行活动进行近似评估。鲁棒调度可分为主动型调度和响应型调度,主动型调度力争在项目开工前就生成具有一定抗干扰能力的基线进度计划,在实际执行时若进度计划被破坏,则需要调用响应型调度对进度计划进行修复,使得实际进度计划与基线进度计划之间的偏差最小[12]。Davari和Demeulemeester[13]指出主动型和响应型调度之间的密切相关性,在工期不确定环境下构建以基线进度计划的成本和所有偏离成本之和最小化为目标的动态规划模型,为RCPSP提供主动-响应型调度策略。Lambrechts等[14-15]通过定义单位资源的平均失败时间和恢复时间对不确定可更新资源可用量进行描述,并设计了禁忌搜索算法获得资源可用量不确定环境下RCPSP的基线进度计划和响应型调度策略。在理论分析不确定资源中断对活动工期影响的基础上,Lambrechts等[16]通过插入时间缓冲的方式构造资源不确定环境下RCPSP的鲁棒基线进度计划。
Zhu等[17]最早对不确定MRCPSP的响应型调度展开研究,针对工期和资源等各类干扰,构建问题的混合整数线性规划模型进行求解。在活动实际开工时间不早于基线进度计划开工时间的假设下,Deblaere等[18]设计了一系列精确算法以及禁忌搜索算法对不确定工期和资源破坏的MRCPSP进度计划进行修复。李佳媛和何正文[19]考虑可更新资源可用量不确定的MRCPSP的主动型调度,通过插入资源缓冲的方式最大化进度计划的鲁棒性。Chakrabortty等[20]区分资源干扰发生前、干扰发生到资源恢复以及资源恢复后三个时段,构建混合整数线性规划模型以便MRCPSP的进度计划在发生资源中断时可以调用。王艳婷等[21]研究活动工期随机中断情况下MRCPSP的主动型和响应型调度的权衡问题,以主动型调度中资源占用成本与响应型调度的调整成本之和的最小化为目标,在基线进度计划鲁棒值合理设定的条件下获得总成本最优的调度方案。
基于以上综述,目前的研究尚存在较大的局限性:(1)现有不确定环境下的随机项目调度都是针对活动工期的不确定,且主要集中于静态策略的研究,虽然已有少量资源不确定的鲁棒调度研究,但资源不确定环境下的随机调度研究尚属空白;(2)相较于不确定RCPSP的研究,由于活动的多模式选择将进一步增加问题的求解难度,导致不确定环境下MRCPSP的研究至今还很少。
本文以最小化项目的期望工期为目标,研究不确定可更新资源可用量环境下的多模式资源受限项目的随机调度问题(Stochastic scheduling of MRCPSP with uncertain resource availabilities,SMRCPSP-URA),主要的创新性工作有:(1)根据问题特点建立由决策阶段、状态空间、决策空间、状态转移函数及目标函数五部分构成的马尔可夫决策过程(Markov decision process,MDP)模型;(2)设计问题的Rollout算法,基准策略为动态的活动-模式优先规则和改进的串行调度生成机制(Serial schedule generation scheme,SSGS)相结合的启发式算法,利用随机资源可用量的蒙特卡洛仿真确定各时段资源可用量的样本数据,综合评估后得到各决策阶段处的最优开工活动集合及其执行模式;(3)通过算例的实验研究,系统分析与资源有关的问题参数、随机资源可用量的不确定参数以及不同优先规则对问题和Rollout算法求解效果和效率的影响,验证算法的有效性。
1 问题描述
本文所研究项目共有n+2个活动,活动0和n+1为虚活动,分别代表项目的开始与结束,V={1,…,n}为项目所有的非虚活动,Pj代表活动j的紧前活动集合。任何非虚活动j的执行模式集合为Mj,其模式m∈Mj的工期为djm,dj=表示活动j的最长工期,T=表示所有活动的最长工期之和。项目执行需要K种可更新资源,活动j的执行模式m对资源k的需求量为rjmk。活动的执行模式唯一,且活动一旦开工其执行模式不再更改。可更新资源k的不确定可用量用随机变量来表示,并且在t-1时刻可以确定资源k在t时段的可用量为Rkt,而无法确定t+1及其之后各时段的可用量。表示项目活动的所有模式对资源k的最大需求量,假设≥LRk,即不会由于资源的随机变化而造成整个项目的停工。不确定可更新资源可用量会导致正在进行的活动被迫发生中断,本文考虑已开工活动仅在资源不足的时候允许被中断,在资源可行时,被中断活动可以继续执行,而无需重新开始(preemptresume)[22]。
基于以上假设,SMRCPSP-URA以最小化项目期望工期为目标,在满足活动间紧前关系、活动的模式选择、随机可更新资源可用量和活动可中断的约束下,动态决策开工活动及其执行模式直至所有活动均完工,最后得到项目调度的满意解。
2 数学模型
马尔可夫决策过程(MDP)是随机环境下序贯决策问题的常用建模方法[23-24],根据以上对本文研究的调度问题的描述,建立如下的MDP模型,主要由五部分构成。
2.1 决策阶段
可更新资源可用量不可行的时刻或某种资源的未占用可用量增多的时刻(包括某活动的完工时刻和某种资源的实际可用量增多的时刻)为决策时刻,例如,若某工程项目某天的施工人员不能满足正在进行的活动对人员的需求,前一天有活动完工,或者有新进的施工人员,则该天为决策时刻。由此,总的决策阶段的个数L≤T,决策阶段i∈{0,…,L-1}的决策时刻记为ti。
2.2 状态空间
决策阶段i的状态定义为Si={Ci,Ai,,γi},其中,Ci和Ai分别表示ti时的已完工活动集合和正在进行的活动集合,为ti时确定的n维活动执行模式向量,为ti时已执行的n维活动工期向量,γi表示ti时实现的K行T列的资源可用量矩阵。初始状态S0={Ø,Ø,,γ0},其中,和均为n维零向量,γ0为项目开工时(0时刻)实现的资源可用量矩阵,第1列表示K种资源在第1时段的可用量,其余T-1列均为零向量。结束状态,其中为所有活动的执行模式向量,=(d1m1,…,dnmn)为所有活动的实际工期向量,γL为项目结束前各时段的资源可用量矩阵。例如,某工程项目需要4种可更新资源,阶段i的决策时刻为第10天,已完工活动为活动1、2和3,工期分别为0天、6天和2天,执行模式分别为1,2和1,正在进行的活动为4和5,都已按照第2种执行模式开工2天,则Ci={1,2,3},Ai={4,5},(1,2,1,2,2,0,…,0),=(0,6,2,2,2,0,…,0),γi的前 4 行 10 列为已实现的所有资源在前10天的可用量。
2.3 决策空间
若Ui=VCi表示ti时未完工的活动集合,则χ(Si)为ti时可以调度的活动x及其所对应的可行模式y所组成的二元向量(x,y)的集合:


该式表明阶段i处,活动x从集合UiAi中选择,若活动x的模式已确定,即¯Mi(x)≠0,则y=¯Mi(x);否则,y应从模式集合Mx中选取。对于可开工活动x及其可行模式y,一方面需要满足紧前关系约束,活动x的所有紧前活动都已经完工;另一方面需要满足资源约束,活动x对资源的需求量与正在进行的活动对资源的需求量之和不超过ti+1时段的资源可用量γi(k,ti+1)。χ(Si)的满足资源约束的所有子集构成决策阶段i处的决策空间,每个可行子集对应决策阶段i处的可开工活动集合Xi和模式集合Yi,用(Xi,Yi)表示,则(Xi,Yi)⊂χ(Si)。
2.4 状态转移函数
若Yi为ti+1到ti+1时刻实现的K行ti+1-ti列的资源可用量矩阵,则定义SM(·)为状态转移函数,即
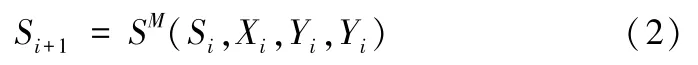
可以看出,Si+1仅与阶段i处的状态Si、决策(Xi,Yi)以及矩阵Yi有关,而与阶段i之前的决策无关,该性质称为马尔可夫性。SM(·)的具体定义如下:

首先,更新Ai∪Xi中任意活动j的已执行工期(j)为与(ti,ti+1)之间的时间间隔之和,以及Xi中第l个活动j的执行模式(j)为Yi(l),由此,可以更新Ci+1为Ci与ti+1时Ai∪Xi中完工活动集合的并集。然后,依据Yi更新资源从ti+2到ti+1+1时段的可用量。最后,若Ai∪XiCi+1中活动对资源的需求量之和大于ti+1时的资源可用量,即资源不可行,则更新Ai+1为空集;否则,表明ti+1时资源可行且某种资源的未占用可用量增多,即Ci+1非空或者某种资源k在ti+1+1时段的可用量大于ti+1时段的可用量,则更新Ai+1为Ai∪Xi中排除Ci+1。
2.5 目标函数
函数g(Si,Xi,Yi,Si+1)=ti+1-ti表示状态Si时决策(Xi,Yi)到状态Si+1所导致项目工期的增加量,则阶段i所对应目标函数可表示为:

上式为从阶段i开始到阶段L-1为止各阶段项目工期的增加量之和的期望。在每个决策阶段i处,随机调度以(4)式的最小化为目标,以期获得最优开工活动和模式集合,根据贝尔曼递归函数(Bellman recursion function)[25]可得到:

表明最优决策()是使得阶段i所对应项目工期的增加量和阶段i+1所对应目标值之和的期望值最小的χ(Si)的子集。
综合以上,基于MDP的SMRCPSP-URA的随机调度过程如图1所示:在资源不可行或某种资源的未占用可用量增多的时刻ti进行决策,依据阶段i处的状态Si,以实现项目期望工期最小化为目标得到(),开工()后,

图1 SMRCPSP-URA的随机调度过程Figure 1 The stochastic scheduling process of SMRCPSP-URA
根据阶段i与i+1之间实现的资源可用量矩阵Yi到达下一个决策状态Si+1,决策过程不断推进,直到所有活动都完工,也就是到达结束状态SL,则调度结束。
3 算法设计
众所周知,以上的大规模MDP模型将面临高维的状态和决策空间,由此导致的“维数灾难”使得传统的随机动态规划算法很难得到(5)式的精确解,因此,需要针对问题特点设计专门的近似动态规划算法寻求高质量的近似解。Rollout是起源于动态规划的一种近似优化方法,实质是基准策略的一个向前迭代的过程,其主要思想是在各决策阶段处应用基准策略对目标(4)进行近似评估,该方法高效且易于操作,已被用于成功解决各类随机调度问题[11,26-27]。本节首先提出Rollout算法的基本框架,然后再详细介绍算法中所采用的基准策略,即基于动态活动-模式优先规则和活动可中断SSGS的启发式算法。
3.1 Rollout算法的框架
表1中展示了Rollout算法的基本框架。在初始化决策阶段、决策时刻、初始状态以及时间计数器t=0后,依据式(1)得到决策阶段处可调度活动及其模式集合χ(Si)。在该集合的元素个数|χ(Si)|非零且不唯一的情况下,对各时段的随机资源可用量进行蒙特卡洛仿真,具体做法如下:首先,根据随机资源可用量的分布情况展开随机抽样,抽样次数为|Ω|,得到各类资源在各时段的可用量样本集,然后,在资源可用量的确定性样本和ti时开工(Xi,Yi)的前提下,采用基准策略对剩余未完工活动进行调度,直至项目结束,得到该资源样本对应的项目工期,最后,计算资源样本集下项目工期的均值,得到ti时开工(Xi,Yi)的项目期望工期。仿真是不确定情形下目标值评估的常用方法,为了减少仿真次数,缩短算法的运行时间,在算法中设置(Xi,Yi)的元素个数为1,在满足资源约束的条件下依次加入使得期望工期最小的活动及其执行模式,直至不能再加入为止,从而得到(,)后开工。不断更新决策阶段,根据t+1时段的资源可用量更新决策时刻,并且依据式(3)更新决策状态,若Si=SL,则算法终止,否则,继续进行调度。

表1 Rollout算法的框架Table 1 The framework of Rollout algorithm
3.2 基准策略
表2 算法中的活动-模式优先规则Table 2 Activity-mode priority rules of algorithm

表2 算法中的活动-模式优先规则Table 2 Activity-mode priority rules of algorithm
类型 规则 极值 公式最晚结束时间(LFT) min LFTj活动优先规则 最晚开始时间(LST) min LFTj-min m∈Mj{djm}最小总时差(MSLK) min LFTj-EFTj最短工期模式(SFM) min djm模式优先规则K最小总资源需求(LTRU) min ∑k=1(rjmk×djm)
进一步,考虑到资源紧缺引起的活动中断对进度计划的影响,对于活动j及其模式m定义如下的中断优先值函数:

上式函数s(j,m)中,MRSmin(j,m)∈[0,1]表示活动j的模式m所需的所有资源在最早可能开工时间ESTj和最迟完工时间LFTj区间内资源强度的最小值。split为0-1变量,如果活动j在ESTj开工会发生中断,则split=1,否则,split=0。δs为算法设定的活动中断参数,若0<MRSmin(j,m)≤δs,表明资源相对紧缺,则活动j的中断被鼓励,否则,资源相对充足,可以推迟活动开工时间而避免中断。由于ESTj和LFTj是动态变化的,所以,中断优先值也是动态的。在标准化活动-模式优先值的基础上再增加式(6)的中断优先值,则形成优先规则 LFT-SFM-SPLIT,LST-SFM-SPLIT,MSLK-SFM-SPLIT,MSLK-LTRU-SPLIT。

表3 活动可中断SSGS的伪代码Table 3 The pseudocode of SSGSwith activity interruption
4 计算实验
4.1 实验设计
为了验证模型和算法的有效性,对PSLIB[30]标准算例库中J30的MRCPSP算例改编后展开计算实验,各活动的模式个数为3,资源种类为2。该算例集是目前库中不确定MRCPSP调度研究测试的最大算例集,含有640个算例。可更新资源系数(RF)反映活动对各类可更新资源的需求状况,取值为0.5和1;可更新资源强度(RS)用于表示活动对每种资源的需要量与资源可用量之间的关系,取值为0.25、0.5、0.75和 1。 Rollout算法用 MATLAB R2018b编译,在CPU主频3.30 GHz,内存为8 GB的个人计算机上运行。
参考随机活动工期变量的设置方法,随机资源可用量的均值为算例中可更新资源的可用量Rk,即E()=Rk,服从以下5种随机分布[8-9]:
(1)U1:区间[LRk,2Rk-LRk]内的均匀分布,方差为(Rk-LRk)2/3;
(2)U2:区间[(Rk+LRk)/2,(3Rk-LRk)/2]内的均匀分布,方差为(Rk-LRk)2/12;
(3)Exp:指数分布,均值为Rk,方差为Rk2;
(4)B1:区间[LRk,2Rk-LRk]内的贝塔分布,方差为(Rk-LRk)2/3;
(5)B2:区间[LRk,2Rk-LRk]内的贝塔分布,方差为(Rk-LRk)2/12。
其中,分布U2和B2的方差最小,U1和B1的方差水平居中,分布Exp的方差最大;U1,U2和Exp是对称分布,B1和B2是非对称分布。分布B1或者B2的对应参数值(α,β)的取值为α=β=1或者11/2。同时,为了有效权衡算法求解质量和效率之间的关系,参考Ballestín[7]的研究设定仿真次数|Ω|=10。
4.2 实验结果分析
实验结果排除Rk<LRk(即上述各随机资源可用量分布区间的下界小于活动最大资源需求量)的三个算例:j3033_9.mm,j3049_1.mm,j3049_2.mm。在随机资源可用量的5种不同分布下,基于8种不同优先规则的Rollout算法求解其余所有算例的项目工期、活动的中断次数和运算时间如表4所示。
考察表4可以看出:
(1)对于随机资源可用量服从U2和Exp分布的项目调度问题,Rollout算法中应该选用的优先规则显然为LSTSFM,相较于其他优先规则,LST-SFM得到的项目工期和活动中断次数都最小;随机资源可用量服从U1和B2分布时,优先规则LFT-SFM对应的项目工期最小,且活动中断次数(分别为5.73和1.74)与最小中断次数(分别为5.58和1.63)之间的差别不大;随机资源可用量服从随机B1分布时,优先规则MSLK-SFM对应最小的项目工期和几乎最小的活动中断次数。这说明基于不同优先规则的Rollout算法在不确定资源可用量的不同情形下的求解效果不同,应该根据随机资源可用量的分布类型和方差大小选择表现最优的优先规则求解。
(2)对于随机资源可用量的5种分布,U2和B2两种分布情况下Rollout算法所得解的项目工期、活动中断次数和算法运算时间最小,U1和B1居中,分布Exp最大。研究结果表明:当不确定资源可用量的方差逐渐增大时,项目工期、活动发生中断的可能性以及调度问题的求解难度也会逐渐增大。
(3)Rollout算法中,不考虑活动中断优先值的优先规则(LFT-SFM,LST-SFM,MSLK-SFM,MSLK-LTRU)的求解效果和效率均优于考虑活动中断优先值的优先规则(LFT-SFMSPLIT,LST-SFM-SPLIT,MSLK-SFM-SPLIT,MSLK-LTRUSPLIT),这说明应该采用不考虑活动中断优先值的优先规则来解决不确定资源可用量环境下的随机项目调度问题。
(4)对比LFT-SFM,LST-SFM,MSLK-SFM三种优先规则,综合考虑项目工期和活动中断次数两方面指标,表现最差的为MSLK-LTRU,但是MSLK-LTRU在运算时间方面具有优势。
前述所提到Buddhakulsomsiri和Kim[22]的研究结果表明,考虑活动中断优先值的优先规则的求解效果要明显优于不考虑活动中断优先值的优先规则,但是,从表4的分析结果(3)可以看出,对于本文所研究的SMRCPSP-URA而言却并非如此。为了进一步检验活动中断优先值对算法求解确定型与不确定型问题效果之间是否存在显著区别,对Rollout算法在采用与不采用活动中断优先值的优先规则之间的项目工期数据进行配对样本T检验,分析结果见表5。假设两组数据之间没有显著差异,并设置置信水平为99%,从表中显著性水平p≈0.00可以看出,两组数据之间存在显著性差异,表明不考虑活动中断优先值的优先规则可以显著提高Rollout算法求解SMRCPSP-URA的绩效。虽然优先规则LFT-SFM,LST-SFM,MSLK-SFM的总体均值都要小于MSLKLTRU,但MSLK-LTRU的标准差最小,表明基于MSLK-LTRU的Rollout算法的表现更加稳定。

表5 基于不同优先规则的Rollout算法是否考虑中断优先值所对应配对样本的T检验Table 5 Paired samp le T tests of Rollout algorithms based on priority rulesw ith and w ithout interruption priority value
4.3 参数分析
为了考察问题参数对Rollout算法求解质量和速度的影响,构建如式(7)的线性回归模型展开分析。

在回归模型中有4个解释变量,x1表示可更新资源系数RF;x2表示可更新资源强度RS;x3表示不确定资源可用量的方差;x4表示SMRCPSP-URA对应的确定型问题项目工期上界与下界之间的相对偏差,代表确定型问题求解的难易程度,偏差大表示求解难度大,偏差小表示求解容易。因变量y分别代表基于不考虑活动中断的优先规则(LFT-SFM,LST-SFM,MSLK-SFM,MSLK-LTRU)的Rollout算法求解的项目工期、活动中断次数和运算时间。回归分析的结果如表6所示,括号中的数字代表系数估计值的标准误差,以上四种因素在5%的显著性水平下的t检验均显著,F检验的p值均为0,衡量指标项目工期、活动中断次数和运算时间用这四种因素表示的拟合度R2均超过60%,表明三种衡量指标都可以较好的用这四种因素来表示。

表6 线性回归分析的结果Table 6 Results of linear regression analysis
以上统计检验的结果表明:(1)活动对可更新资源的需求越大(RF越大),以及不确定资源可用量的变化波动越大越会影响Rollout算法的求解质量,同时也会降低算法的求解效率;(2)可更新资源的供应越充足(RS越大)则越有可能有效提升Rollout算法的求解质量和效率;(3)采用Rollout算法求解SMRCPSP-URA的求解质量会随着其对应确定型问题求解难度的增大而表现出明显的优势,但会导致活动中断次数增大和算法运算时间的增加。
5 结论
本文研究的随机调度问题同时考虑了可更新资源可用量的不确定性、活动执行模式的多样性和资源不确定导致的活动可中断性,将不确定可更新资源的可用量建模为随机变量,以最小化项目的期望工期为目标建立了调度问题的MDP模型,定义可更新资源可用量不可行的时刻或某种资源的未占用可用量增多的时刻为决策时刻,设计了基于动态活动-模式优先规则和活动可中断SSGS的Rollout算法对问题求解,项目管理者可在决策阶段处根据选定的执行模式开工相应的活动直至项目完工。通过大量的算例实验研究,我们得出以下结论:(1)不确定可更新资源可用量的变化波动越大,则项目工期、活动中断次数以及问题的求解难度也会越大;(2)不考虑活动中断优先值的优先规则对随机问题的求解效果要优于考虑活动中断优先值的优先规则;(3)本文所设计的Rollout算法对于解决可更新资源需求小、可更新资源供应充足以及相应的确定型问题求解难度大的算例的效果更好。
本文所研究的SMRCPSP-URA考虑了活动工期的不确定和活动多执行模式,但尚未考虑资源不确定和项目调度多目标等因素,虽然问题会变得更加复杂,但具有更重要的现实应用背景,有待进一步拓展。本文的Rollout算法以优先规则和调度生成机制相结合的启发式算法作为基准策略,简便且易于操作,另外,智能优化算法也是解决大规模问题的有效途径,未来我们将探索更加高效的智能算法作为基准策略以进一步提升Rollout算法的求解性能。
